Skip to main content

Advertisement

Springer Nature Link
Log in

Evaluation of neuro-fuzzy GMDH-based particle swarm optimization to predict longitudinal dispersion coefficient in rivers

  • Original Article
  • Published:
Environmental Earth Sciences Aims and scope Submit manuscript

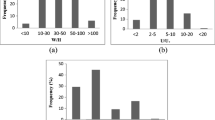
Abstract

In the present research, neuro-fuzzy-based group method of data handling (NF-GMDH) has been applied to evaluate the longitudinal dispersion coefficient in rivers. The NF-GMDH model has been improved through particle swarm optimization algorithms (PSO). Effective parameters on the longitudinal dispersion coefficient including flow depth, channel width, cross-sectional average velocity, and bed shear velocity were selected to characterize a correlation between input and output variables. Field and experimental data sets have been collected from different studies. The efficiency of the proposed NF-GMDH-PSO model for both training and testing stages has been investigated. The performance of the NF-GMDH-PSO model were compared with those obtained from the differential evolutionary (DE), model tree (MT), genetic algorithm (GA), artificial neural network (ANN), and traditional empirical equations. Results analysis showed that among the artificial intelligence approach-based equations, DE and GA methods performed better than the other methodologies. The most accurate empirical equations were also introduced. NF-GMDH-PSO network also predicted the longitudinal dispersion coefficient properly and can be considered as an alternative to the aforementioned successful formulas.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Abbreviations

A :

Cross-sectional area

\(a_{kj}\) :

Constant value for the corresponding fuzzy rule

\(a_{k,j}^{pm}\) :

Parameter of the kth Gaussian function that is utilized for the jth input variable from the mth model and pth layer

B :

Channel width

BIAS:

Bias of the predicted values with respect to the measured ones

\(b_{kj}\) :

A constant value for the corresponding fuzzy rule

\(b_{k,j}^{pm}\) :

Parameter of the kth Gaussian function that is utilized for the jth input variable from the mth model and pth layer

C :

Cross-sectional average concentration

DR:

Discrepancy ratio

E :

Error parameter of the network

\(F_{kj} (x_{j} )\) :

Gaussian membership function of the kth fuzzy rule in the domain of the jth input value x j

f :

A function

H :

Flow depth

h :

Local flow depth

i :

Counter of input data set

j :

Counter of input value or input value

K :

Number of fuzzy rules or Gaussian functions

k :

Counter of fuzzy rule or Gaussian function

k x :

Dispersion coefficient in longitudinal direction

\(k_{{xi\left( {\text{Actual}} \right)}}\) :

ith measured k x value

\(k_{{xi\left( {\text{Model}} \right)}}\) :

Prediction of the ith measured k x value

\(\overline{{k_{x} }}_{{\left( {\text{Actual}} \right)}}\) :

Mean value of the \(k_{{xi\left( {\text{Actual}} \right)}}\) values

\(\overline{{k_{x} }}_{{\left( {\text{Model}} \right)}}\) :

Mean value of the \(k_{{xi\left( {\text{Model}} \right)}}\) values

k y :

Dispersion coefficient in lateral direction

k z :

Dispersion coefficient in orthogonal direction to the bed

M :

Number of partial descriptions in each layer or total number of the measurements

m :

Counter of model

p :

Counter of layer

R :

Correlation coefficient

RMSE:

Root means square error

U :

Cross-sectional average flow velocity

\(U_{*}\) :

Bed shear velocity

\(u'\) :

Deviation of local mean flow velocity from the cross-sectional mean flow velocity

u k :

Compatibility degree of the premise part of the kth fuzzy rule

w k :

Real value for kth fuzzy rule

\(w_{k}^{pm}\) :

Weight parameter of the kth Gaussian function in mth model and pth layer

x :

Coordinate in streamwise direction

x j :

jth input value

y :

Coordinate in lateral direction or final output parameter

\(y^{ * }\) :

Observed value

\(y^{pm}\) :

Output of the mth model in pth layer

\(\varepsilon_{t}\) :

Transverse mixing coefficient

\(\varepsilon_{t0}\) :

Dimensionless transverse mixing coefficient

\(\mu_{k}^{pm}\) :

kth Gaussian function in the mth model and pth layer

\(\prod {}\) :

Algebraic product operator

\(\varSigma\) :

Summation operator

References

  • Abdel-Aal RE, El-Alfy E-SM (2009) Constructing optimal educational tests using GMDH-based item ranking and selection. Neurocomputing 72:1184–1197

    Article  Google Scholar 

  • Abdolrahimi S, Nasernejad B, Pazuki G (2014) Prediction of partition coefficients of alkaloids in ionic liquids based aqueous biphasic systems using hybrid group method of data handling (GMDH) neural network. J Mol Liq 191:79–84

    Article  Google Scholar 

  • Amanifard N, Nariman-Zadeh N, Farahani MH, Khalkhali A (2008) Modeling of multiple short-length-scale stall cells in an axial compressor using evolved GMDH neural networks. Energ Convers Manag 49(10):2588–2594

    Article  Google Scholar 

  • Astakhov VP, Galitsky VV (2005) Tool life testing in gundrilling: an application of the group method of data handling (GMDH). Int J Mach Tool Manu 45:509–517

    Article  Google Scholar 

  • Azamathulla HM, Ab Ghani A (2011) Genetic programming for predicting longitudinal dispersion coefficients in streams. Water Resour Manag 25(6):1537–1544

    Article  Google Scholar 

  • Azamathulla HM, Wu FC (2011) Support vector machine approach for longitudinal dispersion coefficients in natural streams. Appl Soft Comput 11(2):2902–2905

    Article  Google Scholar 

  • Deng ZQ, Singh VP, Bengtsson L (2001) Longitudinal dispersion coefficient in straight rivers. J Hydraul Eng 127(11):919–927

    Article  Google Scholar 

  • Deng ZQ, Bengtsson L, Singh VP, Adrian DD (2002) Longitudinal dispersion coefficient in single-channel streams. J Hydraul Eng 128(10):901–916

    Article  Google Scholar 

  • Elder JW (1959) The dispersion of marked fluid in turbulent shear flow. J Fluid Mech 5(4):544–560

    Article  Google Scholar 

  • Etemad-Shahidi A, Taghipour M (2012) Predicting longitudinal dispersion coefficient in natural streams using M5′ model tree. J Hydraul Eng 138(6):542–554

    Article  Google Scholar 

  • Fischer HB (1967) The mechanics of dispersion in natural streams. J Hydraul Div 93(HY6):187–216

    Google Scholar 

  • Fischer HB (1968) Dispersion predictions in natural streams. J Sanit Eng Div 94(5):927–944

    Google Scholar 

  • Fischer HB (1975) Discussion of simple method for predicting dispersion in streams by R. S. McQuivey and T. N. Keefer. J Environ Eng Div 101(3):453–455

    Google Scholar 

  • Fischer HB, List EJ, Koh RCY, Imberger J, Brooks NH (1979) Mixing in land and costal waters. Academic Press, New York, pp 104–138

    Book  Google Scholar 

  • Graf JB (1995) Measured and predicted velocity and longitudinal dispersion at steady and unsteady flow, Colorado River, Glen Canyon Dam to Lake Mead. J Am Water Resour Assoc 31(2):265–281

    Article  Google Scholar 

  • Guymer I (1998) Longitudinal dispersion in sinuous channel with changes in shape. J Hydraul Eng 124(1):33–40

    Article  Google Scholar 

  • Hwang HS (2006) Fuzzy GMDH-type neural network model and its application to forecasting of mobile communication. Comput Indus Eng 50(4):450–457

    Article  Google Scholar 

  • Iba H, de Garis H (1996) Extending genetic programming with recombinative guidance. In: Angeline P, Kinnear K (eds) Advances in genetic programming, vol 2. MIT Press, Cambridge, pp 69–88

    Google Scholar 

  • Iwasa Y, Aya S (1991) Predicting longitudinal dispersion coefficient in open-channel lows. Proceedings of International Symposium on Environmental Hydraulics, Hong Kong, December 16–18, 1991. A.A. Balkema, Rotterdam, pp 505–510

    Google Scholar 

  • Kalantary F, Ardalan H, Nariman-Zadeh N (2009) An investigation on the Su-NSPT correlation using GMDH type neural networks and genetic algorithms. Eng Geol 104:144–155

    Article  Google Scholar 

  • Kashefipour SM, Falconer RA (2002) Longitudinal dispersion coefficients in natural channels. Water Res 36(6):1596–1608

    Article  Google Scholar 

  • Koussis AD, Rodríguez-Mirasol J (1998) Hydraulic estimation of dispersion coefficient for streams. J Hydraul Eng 124(3):317–320

    Article  Google Scholar 

  • Li X, Liu H, Yin M (2013) Differential evolution for prediction of longitudinal dispersion coefficients in natural streams. Water Resour Manag 27(15):5245–5260

    Google Scholar 

  • Lin JS (2012) A novel design of wafer yield model for semiconductor using a GMDH polynomial and principal component analysis. Expert Syst Appl 39(8):6665–6671

    Article  Google Scholar 

  • Liu H (1977) Predicting dispersion coefficient of streams. J Environ Eng Div 103(1):59–69

    Google Scholar 

  • Madala HR, Ivakhnenko AG (1993) Inductive learning algorithms for complex systems modeling. CRC Press, Boca Raton

    Google Scholar 

  • McQuivey RS, Keefer TN (1974) Simple method for predicting dispersion in streams. J Environ Eng Div 100(4):997–1011

    Google Scholar 

  • Nagasaka K, Ichihashi H, Leonard R (1995) Neuro-fuzzy GMDH and its application to modeling grinding characteristics. Int J Prod Res 33(5):1229–1240

    Article  Google Scholar 

  • Najafzadeh M, Azamathulla HM (2013) Neuro-fuzzy GMDH systems to predict the scour pile groups due to waves. J Comput Civil Eng. doi:10.1061/(ASCE)CP.1943-5487.0000376

    Google Scholar 

  • Najafzadeh M, Lim SY (2015) Application of improved neuro-fuzzy GMDH to predict scour downstream of sluice gates. Earth Sci Inform 8(1):187–196

    Article  Google Scholar 

  • Najafzadeh M, Zahiri A (2015) Neuro-fuzzy GMDH based evolutionary algorithms to predict flow discharge in straight compound channels. J Hydrol Eng. doi:10.1061/(ASCE)HE.1943-5584.0001185

    Google Scholar 

  • Najafzadeh M, Barani GA, Hessami Kermani MR (2013a) Abutment scour in live-bed and clear-water using GMDH Network. Water Sci Technol 67(5):1121–1128

    Article  Google Scholar 

  • Najafzadeh M, Barani GA, Azamathulla HM (2013b) GMDH to predict scour depth around vertical piers in cohesive soils. Appl Ocean Res 40:35–41

    Article  Google Scholar 

  • Nordin CF, Sabol GV (1974) Empirical data on longitudinal dispersion in rivers. Water-resources investigations 74-20. U.S. Geological Survey, Reston

    Google Scholar 

  • Ohtani T, Ichihashi H, Miyoshi T, Nagasaka K (1998) Orthogonal and successive projection methods for the learning of neurofuzzy GMDH. Inform Sci 110:5–24

    Article  Google Scholar 

  • Onwubolu GC (2008) Design of hybrid differential evolution and group method of data handling networks for modeling and prediction. Inform Sci 178(18):3618–3634

    Article  Google Scholar 

  • Papadimitrakis I, Orphanos I (2004) Longitudinal dispersion characteristics of rivers and natural streams in Greece. Water Air Soil Pol Focus 4(4–5):289–305

    Article  Google Scholar 

  • Piasecki M, Katopodes ND (1999) Identification of stream dispersion coefficients by adjoint sensitivity method. J Hydraul Eng 125(7):714–724

    Article  Google Scholar 

  • Riahi-Madvar H, Ayyoubzadeh SA, Khadangi E, Ebadzadeh MM (2009) An expert system for predicting longitudinal dispersion coefficient in natural streams by using ANFIS. Expert Syst Appl 36(4):8589–8596

    Article  Google Scholar 

  • Rutherford JC (1994) River mixing. Wiley, Chichester

    Google Scholar 

  • Sahay RR (2011) Prediction of longitudinal dispersion coefficients in natural rivers using artificial neural network. Environ Fluid Mech 11(3):247–261

    Article  Google Scholar 

  • Sahay RR, Dutta S (2009) Prediction of longitudinal dispersion coefficients in natural rivers using genetic algorithm. Hydrol Res 40(6):544–552

    Article  Google Scholar 

  • Seo IW, Baek KO (2004) Estimation of the longitudinal dispersion coefficient using the velocity profile in natural streams. J Hydraul Eng 130(3):227–236

    Article  Google Scholar 

  • Seo IW, Cheong TS (1998) Predicting longitudinal dispersion coefficient in natural streams. J Hydraul Eng 124(1):25–32

    Article  Google Scholar 

  • Seo IW, Cheong TS (2001) Moment-based calculation of parameters for the storage zone model for river dispersion. J Hydraul Eng 127(6):453–465

    Article  Google Scholar 

  • Taylor GI (1953) Dispersion of soluble matter in solvent flow through a tube. Proc R Soc Lond Ser A 219:186–203

    Article  Google Scholar 

  • Taylor GI (1954) The dispersion of matter in turbulent flow through a pipe. Proc R Soc Lond A 223(1155):446–468

    Article  Google Scholar 

  • Toprak ZF, Cigizoglu HK (2008) Predicting longitudinal dispersion coefficient in natural streams by artificial intelligence methods. Hydrol Processes 22(20):4106–4129

    Article  Google Scholar 

  • Wang HB, Xu AJ, Ai LX, Tian NY (2012) Prediction of endpoint phosphorus content of molten steel in BOF using weighted K-means and GMDH neural network. J Iron Steel Res Int 19(1):11–16

    Article  Google Scholar 

  • Witczak M, Korbicz J, Mrugalski M, Patton RJ (2006) A GMDH neural network-based approach to robust fault diagnosis: application to the DAMADICS benchmark problem. Control Eng Pract 14(6):671–683

    Article  Google Scholar 

  • Yotsukura N, Fischer HB, Sayre WW (1970) Measurement of mixing characteristics of the Missouri River between Sioux City, Iowa and Plattsmouth, Nebraska. U.S. Geological Survey Water-supply paper 1899-G. U.S. Government Printing Office, Washington, DC

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering, Graduate University of Advanced Technology-Kerman, P.O. Box 76315-116, Kerman, Iran

    Mohammad Najafzadeh

  2. Dipartimento di Ingegneria Civile, Università della Calabria, Via P. Bucci, Cubo 42b, 87036, Rende (CS), Italy

    Ali Tafarojnoruz

Authors
  1. Mohammad Najafzadeh
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ali Tafarojnoruz
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Mohammad Najafzadeh.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Najafzadeh, M., Tafarojnoruz, A. Evaluation of neuro-fuzzy GMDH-based particle swarm optimization to predict longitudinal dispersion coefficient in rivers. Environ Earth Sci 75, 157 (2016). https://doi.org/10.1007/s12665-015-4877-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12665-015-4877-6

Keywords