Introduction

The study of disease population dynamics over space and time can help the development of efficient and sustainable strategies and tactics for disease control (Agrios 2004). For successful achievements, it is necessary for the application of methods to represent the disease gradient in space and the disease progress curve over time, considering the relationship between pathogens, hosts, environmental variables, and crop management (Campbell and Madden 1990).

By using models of spatial dependence of an array of observations in space, expressed by semivariograms, it is possible to estimate the occurrence of pest organisms with minimum variance and without bias, through kriging interpolation methodologies (Matheron 1963). Ordinary kriging was used to detect the pattern of spatial dispersion of Colletotrichum lindemuthianum in common bean field (Alves et al. 2004).

A measure of probability of occurrence of C. lindemuthianum in common bean field above or below a certain threshold, according to a control level or a critical pre-determined value, is important for disease assessment in plant pathology. In geostatistics, the indicator kriging method can be used to classify a variable response above or below an established threshold, in a 0 or 1 binary variable. After that, the new variable set is submitted to the indicator semivariogram modeling, which will be used as base for indicator kriging interpolation (Isaaks and Srivastava 1989).

In the study of space–time dynamics of diseases transmitted by seed, there are situations where the disease incidence is evaluated according to its presence or absence in plants, with 0 (absence), 1 (presence) binary code. The indicator kriging approach could be useful to characterize the probability of disease occurrence in plants adopting 0 as threshold value. This methodology can be exploited to characterize anthracnose space–time dynamics, considering the influence of tillage practices on anthracnose development and distribution in bean fields (Hall and Nasser 1996; Ntahimpera et al. 1997) and the effects of inoculum sources of bean anthracnose on yield (Fininsa and Tefera 2002).

This methodology has been already used in the study of areas with probability of occurrence of Armillaria spp. in roots of ponderosa pine, in Black Hills, SD, USA (Kallas et al. 2003). The indicator kriging was also used to study spatial and temporal progress of Phytophthora infestans genotypes in tomatoes and potatoes, in different seasons, at Del Fuerte Valley, Sinaloa, Mexico (Jaime-Garcia et al. 2001).

Thus, starting from the assumption that indicator kriging can be used to study patterns of diseases transmitted by infected seeds, we aimed at characterizing the spatial variability and to map the probability of the incidence of common bean anthracnose using indicator kriging and nonlinear regression.

Material and methods

The tests were conducted in the experimental area of the Plant Pathology Department of the Federal University of Lavras (UFLA). The climatological data were obtained from the INMET climatological station located at the UFLA campus. Before installing the experiments, measures were taken to correct the acidity and to fertilize the experimental plots. Manual weeding and applications of insecticides and fungicides were made, when necessary, to control other pest organisms than anthracnose. The experiment was conducted from April to July 1998 (drought season) and from December 1998 to March 1999 (rainy season). In the drought season, sprinkler irrigation was conducted twice a week, in the amount of 40 mm. An oxicarboxim application was performed for rust control, adopting 15 g per 20 l of water. Lots of susceptible seeds of Carioca cultivar, free of infection by C. lindemuthianum race 89 were selected, based on the roll paper method (Brasil 1992). Two seeds (0.5% of the total), artificially inoculated, considered as point-wise type inoculum source (Campbell and Madden 1990), were sown exactly in the middle of a plot of seven lines, each 6.82-m long. The spacing between lines was 0.5 m, with 11 plants per meter. The seeds were inoculated using a water restriction technique at −1 MPa, at temperature of 20°C, with a light period of 12 h and a dark period of 12 h, inside a BOD, according to Machado et al. (2004) methodology. The non-inoculated seeds were treated with benomyl + thiram before sowing.

Disease incidence assessments were held weekly, 26, 33, 40, 47, 54, and 61 days after sowing (DAS), observing all the plants of the useful area, in a total of 525 observations in each assessment period (Fig. 1).

Fig. 1
figure 1

Location of assessed common bean plants and anthracnose inoculum source

Full size image

The anthracnose incidence hard data were analyzed using geostatistics. A hard datum \( z\left( {{u_\alpha }} \right) \)is a precise measurement of the attribute of interest. There is no uncertainty at the datum location \( {u_\alpha } \); hence, the local prior probabilities are binary (hard) indicator data defined as:

$$ i\left( {{u_\alpha };{z_k}} \right) = \left\{ {\begin{array}{*{20}{c}} {1\;{\hbox{if}}\;z\left( {{u_\alpha }} \right) \leqslant {z_k}} \hfill \\{0\;{\hbox{otherwise}}} \hfill \\\end{array} } \right.\alpha = 1, \ldots, n(u) $$
(1)

The data coding procedure generates an indicator sampling set i(u; z k ) at any sampled location u using the threshold z k value, where 0 refers to absence and 1 to the presence of anthracnose above the action threshold 0.

The experimental indicator semivariogram was estimated as (Goovaerts 1997):

$$ \widehat{\gamma }I\left( {h;\,{z_k}} \right) = \frac{1}{{2N(h)}}{\sum\limits_{\alpha = 1}^{N(h)} {\left[ {i\left( {{u_\alpha };{z_k}} \right) - i\left( {{u_\alpha } + h;{z_k}} \right)} \right]}^2}, $$
(2)

where, \( \widehat{\gamma }I\left( {h;{z_k}} \right) \) is the estimated semivariogram and N(h) the number of observation pairs separated by distance h. The indicator semivariogram measures how often two z-values separated by a vector h are on opposite sides of the threshold value z k .

The empirical semivariogram was fitted by an isotropic spherical model (Olea 2003):

$$ \gamma (h) = \left\{ {\begin{array}{*{20}{c}} {C\left( {\frac{3}{2}\frac{h}{a} - \frac{1}{2}{{\left( {\frac{h}{a}} \right)}^3}} \right)} \hfill & {,0 \leqslant h < a} \hfill \\C \hfill & {,h \geqslant a,} \hfill \\\end{array}, } \right. $$
(3)

where, C is the sill, a the range, and h the distance. The spherical model exhibits a linear behavior near the origin but flattens out at larger distances and reach the sill at h = a. The scale parameter a of the spherical models coincides with the range (Isaaks and Srivastava 1989; Chilès and Delfiner 1999).

The weighted least squares method was used for semivariogram theoretical models fit according to Cressie (1985) methodology.

The spatial dependence degree index (SDDI) was estimated based on sill (C) and nugget values (C 0) using the same classification adopted by Alves et al. (2004):

$$ {\hbox{SDDI}} = \frac{{{C_0}}}{{{C_0} + C}} \times 100, $$
(4)

where when SDDI ≤25%, a strong spatial dependence is present, when 25% ≤ SDDI ≤ 75%, a moderate spatial dependence is present, when finally SDDI ≥ 75%, a weak dependence is present.

The kriging estimator can be expressed as a linear combination of indicator random variables. The indicator estimator at any location u, for a given threshold value z k (Goovaerts 1997), is given by:

$$ {\left[ {I\left( {u;{z_k}} \right)} \right]^*} - E\left\{ {I\left( {u;{z_k}} \right)} \right\} = \sum\limits_{\alpha = 1}^{n(u)} {{\lambda_\alpha }\left( {u;{z_k}} \right)\left[ {I\left( {{u_\alpha };{z_k}} \right) - E\left\{ {I\left( {{u_\alpha };{z_k}} \right)} \right\}} \right]} $$
(5)

where \( {\lambda_\alpha }\left( {u;{z_k}} \right) \) is the weight assigned to the indicator datum \( i\left( {{u_\alpha };{z_k}} \right) \), considered as a realization of the indicator random variable \( I\left( {{u_\alpha };{z_k}} \right) \).

The ordinary indicator kriging estimator can consider the local fluctuations of the indicator mean by limiting the domain of stationary of that mean to the local neighborhood W(u):

$$ E{\left\{ {I{\left( {u\prime ;{\text{z}}_{{\text{k}}} } \right)}} \right\}} = {\text{constant}}\;{\text{but}}\;{\text{unknown}}\;\forall u\prime \; \in \;{\text{W}}{\left( {\text{u}} \right)}, $$
(6)

thus, it is a linear combination of n(u) random variables \( I\left( {{u_\alpha };{z_k}} \right) \) in the neighborhood W(u) (Cressie 1993; Goovaerts 1997):

$$ \left[ {F\left( {u;{z_k}(n)} \right)} \right]_{\rm{oIK}}^{*} = \left[ {I\left( {u;{z_k}} \right)} \right]_{\rm{OK}}^* = \sum\limits_{\alpha = 1}^{n(u)} {\lambda_\alpha^{\rm{OK}}\left( {u;{z_k}} \right)I\left( {{u_\alpha };{z_k}} \right)}, $$
(7)

where the weights λ are given by an ordinary kriging system of type

$$ \left\{ {\begin{array}{*{20}{c}} {\sum\limits_{\beta = 1}^{n(u)} {\lambda _\beta ^{OK}} \left( {u;{z_k}} \right){C_I}\left( {{u_\alpha } - {u_\beta };{z_k}} \right) + {\mu _{OK}}\left( {u;{z_k}} \right) = {C_I}\left( {{u_\alpha } - u;{z_k}} \right)} \hfill \\{\;\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \alpha = 1,...,n\left( u \right)} \hfill \\{\sum\limits_{\beta = 1}^{n(u)} {\lambda _\beta ^{OK}} \left( {u;{z_k}} \right) = 1} \hfill \\\end{array} } \right. $$
(8)

where C I (h;z k ) is the covariance function of the indicator random function I I (u;z k ) at the threshold z k .

Accounting for the relation C(h) = C(0) – γ(h), the ordinary indicator kriging system was expressed in terms of semivariograms as

$$ {\begin{array}{*{20}{c}} {\sum\limits_{\beta = 1}^{n\left( u \right)} {\lambda _\beta ^{{\rm{OK}}}} \left( {u;{z_k}} \right)\left[ {C\left( 0 \right) - \gamma \left( {{u_\alpha } - {u_\beta };{z_k}} \right)} \right] + {\mu _{OK}}\left( {u;{z_k}} \right) = C\left( 0 \right) - \gamma \left( {{u_\alpha } - u;{z_k}} \right)} \hfill \\{\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \alpha = 1,...,n\left( u \right)} \hfill \\{\sum\limits_{\beta = 1}^{n\left( u \right)} {\lambda _\beta ^{{\rm{OK}}}} \left( {u;{z_k}} \right) = 1} \hfill \\\end{array} } $$
(9)

Considering the non-bias condition \( \sum\nolimits_{\beta = 1}^{n(u)} {\lambda_\beta^{OK}(u) = 1} \), the variance term C(0) cancels out from the first n(u) equations, generating the following equation:

$$ \left\{ {\begin{array}{*{20}{c}} {\sum\limits_{\beta = 1}^{n\left( u \right)} {\lambda _\beta ^{OK}} \left( {u;{z_k}} \right)\gamma \left( {{u_\alpha } - {u_\beta };{z_k}} \right) - {\mu _{OK}}\left( {u;{z_k}} \right) = \gamma \left( {{u_\alpha } - u;{z_k}} \right)} \hfill \\{\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {\kern 1pt} \quad \;\;\alpha = 1,...,n\left( u \right)} \hfill \\{\sum\limits_{\beta = 1}^{n\left( u \right)} {\lambda _\beta ^{OK}} \left( {u;{z_k}} \right) = 1} \hfill \\\end{array} } \right. $$
(10)

Kriging was performed adopting up to five neighbors with eight angular sectors of search. The indicator kriging estimates were evaluated using cross-validation analysis. The cross-validation is a powerful validation technique used to check the performance of the kriging model. It consists in removing data, one at a time, and then trying to predict it (Alves et al. 2008). Thus, the observed values can be compared to the predicted values in order to assess how well the prediction is working according to kriging system self-consistency (Alves et al. 2008; Isaaks and Srivastava 1989; Cressie 1993; Goovaerts 1997; Chilès and Delfiner 1999; Burrough and McDonnell 1998). The mean standardized (MS) prediction errors were defined by

$$ \frac{{\sum\limits_{\alpha = 1}^n {\left( {\left( {\hat{Z}\left( {{u_\alpha }} \right) - Z\left( {{u_\alpha }} \right)} \right)/\hat{\sigma }\left( {{u_\alpha }} \right)} \right)} }}{n}, $$
(11)

and the root mean square standardized prediction errors (RMS) were defined by:

$$ \sqrt {{\frac{{\sum\limits_{\alpha = 1}^n {{{\left[ {\left( {\hat{Z}\left( {{u_\alpha }} \right) - Z\left( {{u_\alpha }} \right)} \right)/\hat{\sigma }\left( {{u_\alpha }} \right)} \right]}^2}} }}{n}}}, $$
(12)

where \( \hat{Z}\left( {{u_\alpha }} \right) \) is the kriging estimation, \( Z\left( {{u_\alpha }} \right) \) is the observed value, \( \hat{\sigma }\left( {{u_\alpha }} \right) \) is the prediction standard error for \( {u_\alpha } \) location. Approximately, mean standardized prediction errors should be 0 and root mean square standardized prediction errors should be 1 (Cressie 1993).

The time series pattern of diseased plants over time was modeled with nonlinear regression. The nonlinear least squares formulation was used to fit a nonlinear model to data. In matrix form, nonlinear models are given by the equation: \( y = f\left( {X,\beta } \right) + \varepsilon \), where y is a n-by-1 vector of responses, f is a function of ß and X, ß is a m-by-1 vector of coefficients, X is the n-by-m design matrix for the model, and ε is a n-by-1 vector of errors. An iterative approach was used to fit the models coefficients involving a heuristic approach to produce reasonable starting values for the calculation of the Jacobian of f(X,B) and the estimate of the coefficients, whether the fit was improved by the trust-region algorithm. The trust-region algorithm was adopted because it can solve difficult nonlinear problems more efficiently than other algorithms, and it represents an improvement over the popular Levenberg–Marquardt algorithm (Branch et al. 1999; Marquardt 1963). The r-square (R2), adjusted r-square (adj.R 2), and root mean squared error (RMSE) statistic measures were used to verify how successful the fit was in explaining the variation of the anthracnose incidence data. The R 2 and adj.R 2 with a value closer to 1 and a RMSE value closer to 0 indicate a better model fit (Draper and Smith 1998).

Results

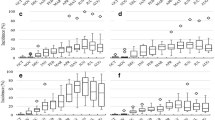
Spherical isotropic indicator semivariograms enabled to characterize the spatial pattern of anthracnose in the rainy and drought seasons at 26, 33, 40, 47, 54, and 61 days after sowing of common bean in the field. The strength of spatial dependence degree index tends to increase with time in the rainy season. Otherwise, in the drought season, the strength of spatial dependence degree oscillates with high and low values over time. The range and sill parameters of the semivariograms also tend to increase over time and were higher in drought than in rainy periods (Figs. 2 and 3).

Fig. 2
figure 2

Indicator semivariograms of incidence of anthracnose in common bean, at 26, 33, 40, 47, 54, and 61 DAS, in the rainy season. Nugget effect (C o ), sill (C), range (a), spatial dependence degree index (SDDI), mean standardized prediction errors (MS), root mean square standardized prediction errors (RMS)

Full size image
Fig. 3
figure 3

Indicator semivariograms of incidence of anthracnose in common bean, at 26, 33, 40, 47, 54, and 61 days after sowing (DAS), in the drought season. Nugget effect (C o ), sill (C), range (a), spatial dependence degree index (SDDI), mean standardized prediction errors (MS), root mean square standardized prediction errors (RMS)

Full size image

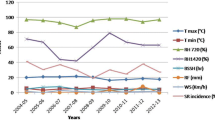
The indicator kriging technique, using the fitted range and sill parameters of isotropic indicator semivariogram, presented satisfactory performance to map the spatial variability of common bean anthracnose along the time based on kriging error coefficients, considering that the mean standardized prediction errors and the root mean square standardized prediction errors presented values near to 0 and 1, respectively, according to ideal conditions of the estimator related by Cressie (1993, p. 101; Figs. 2 and 3). Thus, the assumption of isotropy could be applied to explain the disease progress. According to kriging probability maps, the disease was disseminated around the primary inoculum source presenting strongly aggregated pattern in the rainy season (Fig. 4). In the drought period, the disease presented higher aggressiveness, spreading with secondary inoculum sources that became coalescent along the time, characterizing its polycyclic nature (Fig. 5). The influence of climatic factors, such as the favorable temperature with average value of 19.0°C, associated with sprinkler irrigation, may have favored the higher anthracnose progress in the drought period than in the rainy one. In the rainy period, the higher frequency of rainy days associated to an average temperature that reaches a maximum of 28.0°C may have induced the aggregated pattern of anthracnose in the field (Table 1).

Fig. 4
figure 4

Indicator kriging maps of probability of incidence of anthracnose in common bean, in the rainy season, at 26, 33, 40, 47, 54, and 61 days after sowing (DAS)

Full size image
Fig. 5
figure 5

Indicator kriging maps of probability of incidence of anthracnose in common bean, in the drought season, at 26, 33, 40, 47, 54, and 61 days after sowing (DAS)

Full size image
Table 1 Monthly average values of maximum, mean, and minimum air temperature (maxT, T, minT; degrees Celsius), monthly total rainfall (millimeter), monthly average relative humidity (percent), and monthly average insolation (hours) from April 1998 to March 1999, at principal INMET climatological station of Lavras, Minas Gerais
Full size table

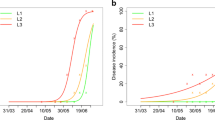
Nonlinear power regression models enabled to characterize the range parameters of the semivariograms of anthracnose in each considered period. Power models presented satisfactory fit to describe the epidemic progress, during rainy and drought seasons, based on the r-square and root mean square error coefficients. The power models enabled to characterize the disease progress curve along the time, with differences between anthracnose progress in drought and rainy periods, according to the higher values in drought than in rainy period, represented by the pattern of curves inflection (Fig. 6).

Fig. 6
figure 6

Nonlinear regression models adjusted to the range values of anthracnose incidence semivariograms at 26, 33, 40, 47, 54, and 61 DAS, in the rainy (a) and drought (b) seasons

Full size image

Discussion

The structured behavior of semivariograms can be related to the pattern of anthracnose distribution, forming clusters near the plants that became infected in the field. The increase of range and sill parameters of semivariograms along time was possibly influenced by the disease progress from the primary and secondary sources of inoculum. The range and sill parameters were higher in the drought season than in the rainy one, and this can be a consequence of the higher infection of common bean plants in the drought period. The strength of the spatial dependence degree index tended to increase with time in the rainy season and can be related to the uniformity of disease dispersion in this period, always over the primary source of inoculum established in the experimental plot. Otherwise, in the drought season, the strength of spatial dependence degree oscillated with high and low values over the time, possibly due to the formation of secondary focus of common bean diseased plants in the field. Alves et al. (2004) studied the severity of cotton ramulosis and common bean anthracnose, in the rainy season, using spherical and Gaussian semivariograms and also observed increase of range and sill parameters along time. According to the authors, the pattern of plants infection in the field was also influenced by the formation of primary and secondary sources of inoculum over the evaluated periods.

The indicator kriging maps enabled to detect the aggregated pattern of anthracnose epidemic in a similar manner as verified by Alves et al. (2004), using ordinary kriging and by Pinto et al. (2001), using quadrat maps. However, quadrats technique did not enable to study the probability of occurrence of the disease in the field, to quantify its spatial dependence degree, structure and magnitude of spatial dependence, prediction errors and to map the disease progress using a known scale of representation. Considering the present results, based on kriging probability maps, the disease was disseminated around the primary inoculum source presenting strongly aggregated pattern in the rainy season. In the drought period, the disease presented higher aggressiveness, spreading with secondary inoculum sources that became coalescent along the time, characterizing its polycyclic nature (Fig. 5). The influence of climatic factors, such as the favorable temperature with average value of 19.0°C, associated to sprinkler irrigation, may have favored higher progress of anthracnose in drought than in rainy period. In the rainy period, the major intensity of rainy days associated to average maximum temperature of 28.0°C may have induced the aggregated pattern of anthracnose in the field (Table 1). Tu (1982) also observed that bean plants inoculated with C. lindemuthianum and incubated at different conditions of temperature, presented higher severity at 20–24°C and minor severity at 16°C and 28–32°C. Araya Fernandez et al. (1987) studied the inoculation of C. lindemuthianum in common bean Manteigão Fosco 11, at Zona da Mata, Minas Gerais, in the rainy and drought season and also observed minor infected pods in the rainy season because the rainfall led the vigorous growth of common bean, determining more dense canopy and stronger protection of the pods from the rain drops. The authors verified minor vegetative growth of common bean in the drought season, exposing the pods to the inoculums and rain drops, favoring the disease progress. However, the authors did not use any kriging methodology to describe the space–time pattern of disease in the field.

In relation to the nonlinear methodology of kriging adopted in the present study, Jaime-Garcia et al. (2001) also have used indicator kriging to study the space–time progress of P. infestans in tomatoes and potatoes. According to the authors, indicator semivariograms and kriging maps enabled to observe climate effects on late blight progress, in different seasons.

Considering the distribution of anthracnose in the field along the time, power models presented satisfactory performance to describe disease progress curve with time (Fig. 6), confirming the results of the kriging maps. Similarly, Aylor and Ferrandino (1989) also have used nonlinear regression models to study temporal development of bean rust epidemics. According to the authors, the exponential law model described the increase of pustules per plant with time, during the years of 1986 and 1987, presenting r-squared values of 0.997 and 0.990, respectively.

Thus, considering that nonlinear geostatistics and nonlinear regression techniques were useful to characterize the pattern of variability of common bean in different periods of evaluation and conditions of field management, based on indicator semivariograms, probability maps and power models of disease space–time variability, the presented results could be useful to demonstrate the imminent risk of popularization in the use of seeds without proper control of health quality and can serve as a basis to establish sanitary standards for seed health analysis of common bean anthracnose. The indicator kriging can be adopted as an alternative method for disease monitoring and precision disease management, providing positive responses to overcoming the challenges, both at national and international levels, about standards of tolerance of seed-borne common bean anthracnose.

Conclusions

Space–time patterns of anthracnose progress were influenced by weather conditions and sprinkler irrigation.

Spherical semivariogram models and kriging probability maps enable to characterize anthracnose spatial variability and dynamic in the field.

Power models presented satisfactory fit to describe the progress of anthracnose along the time, based on range values, during rainy and drought seasons.