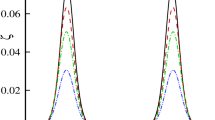Abstract
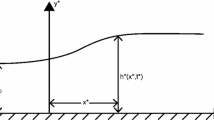
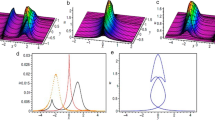
A comprehensive theoretical study on the head-on collision between two solitary waves in a thin elastic plate floating on an inviscid fluid of finite depth is investigated analytically by means of a singular perturbation method. The effects of plate compression are also taken into account. The Poincaré–Lighthill–Kuo method has been used to derive the solution up to the fourth order of the resulting nonlinear differential equation, which in principle gives the asymptotic series solution. It is found that after collision, both the hydroelastic solitary waves preserves their original shape and positions. However a collision does have imprints on colliding waves with non-uniform phase shift up to the third order which creates tilting in the wave profile. Maximum run-up amplitude, wave speed, phase shift and distortion profile have also been calculated and plotted for two colliding solitary waves.










Similar content being viewed by others
References
Forbes, L.K.: Surface waves of large amplitude beneath an elastic sheet. Part 1. High-order series solution. J. Fluid Mech. 169, 409–428 (1986)
Forbes, L.K.: Surface waves of large amplitude beneath an elastic sheet. Part 2. Galerkin solution. J. Fluid Mech. 188, 491–508 (1988)
Părău, E.I., Vanden-Broeck, J.M.: Three-dimensional waves beneath an ice sheet due to a steadily moving pressure. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 369(1947), 2973–2988 (2011)
Deike, L., Bacri, J.C., Falcon, E.: Nonlinear waves on the surface of a fluid covered by an elastic sheet. J. Fluid Mech. 733, 394–413 (2013)
Chen, X.J., Wu, Y.S., Cui, W.C., Tang, X.F.: Nonlinear hydroelastic analysis of a moored floating body. Ocean Eng. 30(8), 965–1003 (2003)
Plotnikov, P.I., Toland, J.F.: Modelling nonlinear hydroelastic waves. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 369(1947), 2942–2956 (2011)
Blyth, M.G., Pru, E.I., Vanden-Broeck, J.M.: Hydroelastic waves on fluid sheets. J. Fluid Mech. 689, 541–551 (2011)
Vanden-Broeck, J.M., Părău, E.I.: Two-dimensional generalized solitary waves and periodic waves under an ice sheet. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 369(1947), 2957–2972 (2011)
Milewski, P.A., Vanden-Broeck, J.M., Wang, Z.: Hydroelastic solitary waves in deep water. J. Fluid Mech. 679, 628–640 (2011)
Guyenne, P., Părău, E.I.: Forced and unforced flexural-gravity solitary waves. Procedia IUTAM 11, 44–57 (2014)
Alam, M.R.: Dromions of flexural-gravity waves. J. Fluid Mech. 719, 1–13 (2013)
Sorensen, M.P., Christiansen, P.L., Lomdahl, P.: Solitary waves on nonlinear elastic rods. I. J. Acoust. Soc. Am. 76(3), 871–879 (1984)
Dai, S.Q.: The interaction of two pairs of solitary waves in a two-fluid system. Sci. China Math. 81(6), 1718–1722 (1984)
Sorensen, M.P., Christiansen, P.L., Lomdahl, P., Skovgaard, O.: Solitary waves on nonlinear elastic rods. II. J. Acoust. Soc. Am. 81(6), 1718–1722 (1987)
Huang, G., Lou, S., Xu, Z.: Head-on collision between two solitary waves in a Rayleigh–Benard convecting fluid. Phys. Rev. E 47(6), R3830 (1993)
Huang, G., Velarde, M.G.: Head-on collision of two concentric cylindrical ion acoustic solitary waves. Phys. Rev. E 53(3), 2988 (1996)
Dai, H.H., Dai, S.Q., Huo, Y.: Head-on collision between two solitary waves in a compressible mooneyrivlin elastic rod. Wave Motion 32(2), 93–111 (2000)
Părău, E.I., Dias, F.: Nonlinear effects in the response of a floating ice plate to a moving load. J. Fluid Mech. 460, 281–305 (2002)
Demiray, H.: Head-on-collision of nonlinear waves in a fluid of variable viscosity contained in an elastic tube. Chaos Solitons Fract. 41(4), 1578–1586 (2009)
Ozden, A.E., Demiray, H.: Re-visiting the head-on collision problem between two solitary waves in shallow water. Int. J. Non-Linear Mech. 69, 66–70 (2015)
Laitone, E.V.: The second approximation to cnoidal and solitary waves. J. Fluid Mech. 9, 430–444 (1960)
Grimshaw, R.: The solitary wave in water of variable depth. Part 2. J. Fluid Mech. 46, 611–622 (1971)
Gardner, C.S., Greene, J.M., Kruskal, M.D., Miura, R.M.: Method for solving the Korteweg–deVries equation. Phys. Rev. Lett. 19(19), 1095 (1967)
Lighthill, M.J.: A technique for rendering approximate solutions to physical problems uniformly valid. Philosophical Magaz. Ser. 7. 40(5), 1179–1120 (1949)
Lin, C.C.: On a perturbation theory based on the method of characteristics. J. Math. Phys. 33, 117–134 (1954)
Su, C.H., Mirie, R.M.: On head-on collisions between two solitary waves. J. Fluid Mech. 98, 509–525 (1980)
Kuo, Y.H.: On the flow of an incompressible viscous fluid past a flat plate at moderate Reynolds number. J. Math. Phys. 32, 81–101 (1953)
Dai, S.Q.: Poincare–Lighthill–Kuo method and symbolic computation. Appl. Math. Mech. Engl. Ed. 22(3), 261–269 (2001)
Van Dyke, M.: Perturbation methods in fluid mechanics/annotated edition. NASA STI/Recon Technical Report A 75, 46926 (1975)
Zhu, Y., Dai, S.Q.: On head-on collision between two GKDV solitary waves in a stratified fluid. Acta Mech. Sin. 7(4), 300–308 (1991)
Zhu, Y.: Head-on collision between two mkdv solitary waves in a two-layer fluid system. Appl. Math. Mech. Engl. Ed. 13(5), 407–417 (1992)
Xia, X., Shen, H.T.: Nonlinear interaction of ice cover with shallow water waves in channels. J. Fluid Mech. Engl. Ed. 467, 259–268 (2002)
Bhatti, M.M., Lu, D.Q.: Effect of compression on the head-on collision between two hydroelastic solitary waves. In: Proceedings of the 12th International Conference on Hydrodynamics. Egmond aan Zee, The Netherlands (2016)
Guyenne, P., Părău, E.I.: Finite-depth effects on solitary waves in a floating ice sheet. J. Fluids Struct. 49, 242–262 (2014)
Acknowledgements
This research was sponsored by the National Natural Science Foundation of China under Grant No. 11472166. The authors are indebted to the reviewer for his/her critical comments that led to improvement in the work.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Equation of \(O(\epsilon ^3 )\)
Appendix B: Expressions of the Coefficients
Rights and permissions
About this article
Cite this article
Bhatti, M.M., Lu, D.Q. Head-on Collision Between Two Hydroelastic Solitary Waves in Shallow Water. Qual. Theory Dyn. Syst. 17, 103–122 (2018). https://doi.org/10.1007/s12346-017-0263-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12346-017-0263-y