Skip to main content
SpringerLink
Log in

Design and simulation of double-mass dynamic vibration absorber with residual vibration mode

  • Original Article
  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

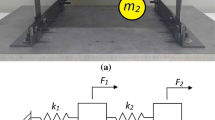
This paper presents a double-mass dynamic vibration absorber (DVA) that rapidly reduces the motion of the object to be damped (main system) and converts it to the motion of the DVA. In this way, the DVA attenuates the vibration of the main system. A DVA is usually designed to improve the resonance amplitude and convergence time of the main system vibration, and the kinetic energy of the main system is dissipated as heat in the damping element of the DVA. We describe a novel configuration consisting of two DVAs connected by a spring and an inerter. This new structure enables a rapid response reduction of the main system and residual vibration in the DVA. By tuning the responses of both the main system and the DVA, two vibration modes can be realized: a damping mode and a residual vibration mode. The proposed device is optimized using a genetic algorithm and applied to a bridge to demonstrate its performance.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

a 1n, a 2n :

Parameters for fitness function

b n :

Dimensionless evaluation value

c 1 :

Damping coefficient of the main system

c 2, c 3, c 4 :

Damping coefficients of the DVAs

f b :

Frequency of mode B

f m :

Frequency of the main system

g n :

Target value

k 1 :

Stiffness coefficient of the main system

k 2, k 3, k 4 :

Stiffness coefficients of the DVAs

m 1 :

Mass of the main system

m 2, m 3 :

Mass of the DVAs

r 1 :

Lower limit of tolerance for evaluation value

r u :

Upper limit of tolerance for evaluation value

s 1∼s 7 :

Genes of genetic algorithm

x 0 :

Absolute displacement of the motion excitation

x 1 :

Absolute displacement of the main system

x 2, x 3 :

Absolute displacements of the DVAs

y 1 :

Relative displacement of the main system

y 2, y 3 :

Relative displacements of the DVAs

μ :

Mass ratio of DVA to main system

ψ :

Inertial mass of an inerter

λ 1, λ 2 :

Component of eigenmode vector

ω b :

Non-damped natural angular frequency of mode B

ζ A1, ζ A2 :

Damping ratios of mode A

ζ B :

Damping ratio of mode B

References

  1. M. Sanati, S. E. Khadem, S. Mirzabagheri, H. Sanati and M. Y. Khosravieh, Performance evaluation of a novel rotational damper for structural reinforcement steel frames subjected to lateral excitations, Earthquake Engineering and Engineering Vibration, 13 (2014) 75–84, DOI: https://doi.org/10.1007/s11803-014-0213-5.

    Article  Google Scholar 

  2. D. Guan, X. Jing, H. Shen, L. Jing and J. Gong, Test and simulation the failure characteristics of twin tube shock absorber, Mechanical Systems and Signal Processing, 122 (2019) 707–719.

    Article  Google Scholar 

  3. T. Nakai, H. Kurino, T. Yaguchi and N. Kano, Control effect of large tuned mass damper used for seismic retrofitting of existing high-rise building, Japan Architectural Review, 2(3) (2019) 269–286.

    Article  Google Scholar 

  4. K. Watanabe, N. Miura and A. Sone, Development of active vibration damping device adjusting TMD to various periodic bands of seismic waves, Proceedings of the ASME 2019 Pressure Vessels and Piping Conference, Volume 8: Seismic Engineering, San Antonio, Texas, USA (2019).

  5. K. Takeya, E. Sasaki, H. Iwabuki, K. Nagafune, H. Hora and T. Nagoya, Development of a tuned mass generator for energy harvesting using bridge vibration, Journal of Japan Society of Civil Engineers, Ser. A1 (Structural Engineering and Earthquake Engineering (SE/EE)), 72(2) (2016) 290–301 (in Japanese).

    Google Scholar 

  6. A. Masuda and F. Zhao, Miniaturized broadband vibration energy harvester with piecewise-linear asymmetric restoring force, Proceedings of the ASME 2019 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Louisville, USA (2019).

  7. J. Ormondroyd and J. P. Den Hartog, The theory of the dynamic vibration absorber, Applied Mechanics, 50(7) (1928) 9–22.

    Google Scholar 

  8. T. Asami, Calculation of the H∞ optimized design of a single-mass dynamic vibration absorber attached to a damped primary system, Mechanical Engineering Journal, 7(5) (2020) 1–12.

    Article  Google Scholar 

  9. S. H. Crandall and W. D. Mark, Random Vibration in Mechanical Systems, Academic Press (1963) 55–101.

  10. H. Yamaguchi, Damping of transient vibration by a dynamic absorber, Transactions of the Japan Society of Mechanical Engineers Series C, 54(499) (1988) 561–568, DOI: https://doi.org/10.1299/kikaic.54.561 (in Japanese).

    Article  Google Scholar 

  11. O. Nishihara and H. Matsuhisa, Design and tuning of vibration control devices via stability criterion, Proceedings of Dynamics and Design Conference, Tokyo, Japan, 10(1) (1997) 165–168 (in Japanese).

    Google Scholar 

  12. T. Asami, K. Yamada and N. Kawaguchi, A quasi-optimal design formula of a parallel-type double-mass dynamic vibration absorber based on the stability criterion, Mechanical Engineering Journal, 8(3) (2021) 1–14, DOI: https://doi.org/10.1299/mej.20-00545.

    Google Scholar 

  13. T. Asami and K. Yamada, Numerical solutions for optimal double-mass dynamic vibration absorbers attached to a damped primary system, Mechanical Engineering Journal, 7(2) (2020) 1–20, DOI: https://doi.org/10.1299/mej.19-00051.

    Google Scholar 

  14. X. T. Nguyen, N. Miura, V. T. Nguyen and T. L. Bui, Design of multiple tuned mass damper devices and application to response control of bridge under external force, Mechanics Based Design of Structures and Machines (2021) 1–18, DOI: https://doi.org/10.1080/15397734.2021.2002163.

  15. P. Wielgos and R. Gerylo, Optimization of multiple tuned mass damper (MTMD) parameters for a primary system reduced to a single degree of freedom (SDOF) through the modal approach, Applied Sciences, 11(4) (2021) 1–28, DOI: https://doi.org/10.3390/app11041389.

    Article  Google Scholar 

  16. T. P. Huu, N. Miura and D. Iba, Multi active tuned mass dampers for earthquake-induced vibration response control of high rise building, Journal of Mechanical Science and Technology, 36 (2022) 1655–1666, DOI: https://doi.org/10.1007/s12206-022-0304-6.

    Article  Google Scholar 

  17. M. C. Smith, Synthesis of mechanical networks: the inerter, IEEE Transactions on Automatic Control, 47(10) (2002) 1648–1662, DOI: https://doi.org/10.1109/TAC.2002.803532.

    Article  MathSciNet  MATH  Google Scholar 

  18. S. Kawamata, M. Yoneda and Y. Hangai, Development of a vibration control system for structures by means of “mass pumps”, Bulletin of Earthquake Resistant Structure Research Center, University of Tokyo (1973) 1–15.

  19. R. Tuluie, Fluid Inerter, U.S. Patent 13/575017 (2010).

  20. M. C. Smith and F. C. Wang, Performance benefits in passive vehicle suspensions employing inerters, Vehicle System Dynamics, 42(4) (2004) 235–257, DOI: https://doi.org/10.1109/CDC.2003.1272

    Article  Google Scholar 

  21. F. C. Wang and W. J. Su, Impact of inerter nonlinearities on vehicle suspension control, Vehicle System Dynamics, 46(7) (2008) 575–595, DOI: https://doi.org/10.1080/00423110701519031.

    Article  Google Scholar 

  22. K. Ikago, K. Saito and N. Inoue, Seismic control of single-degree-of-freedom structure using tuned viscous mass damper, Earthquake Engineering and Structural Dynamics, 41 (2012) 453–474, DOI: https://doi.org/10.1002/eqe.1138.

    Article  Google Scholar 

  23. L. Marian and A. Giaralis, Optimal design of inerter devices combined with TMDs for vibration control of buildings exposed to stochastic seismic excitations, Proceedings of the 11th International Conference on Structural Safety and Reliability, New York, USA (2013) 1–8.

  24. D. Pietrosanti, M. De Angelis and M. Basili, Optimal design and performance evaluation of systems with tuned mass damper inerter (TMDI), Earthquake Engineering and Structural Dynamics, 46 (2017) 1367–1388, DOI: https://doi.org/10.1002/eqe.2861.

    Article  Google Scholar 

  25. A. Giaralis and A. A. Taflanidis, Optimal tuned mass-damper-inerter (TMDI) design for seismically excited MDOF structures with model uncertainties based on reliability criteria, Structural Control and Health Monitoring, 25(2) (2018) 1–22, DOI: https://doi.org/10.1002/stc.2082.

    Article  Google Scholar 

  26. I. F. Lazar, S. A. Neild and D. J. Wagg, Using an inerter-based device for structural vibration suppression, Earthquake Engineering and Structural Dynamics, 43 (2014) 1129–1147, DOI: https://doi.org/10.1002/eqe.2390.

    Article  Google Scholar 

  27. C. Pan, R. Zhang, H. Luo, C. Li and H. Shen, Demand-based optimal design of oscillator with parallel-layout viscous inerter damper, Structural Control and Health Monitoring, 25(1) (2018) 1–15, DOI: https://doi.org/10.1002/stc.2051.

    Article  Google Scholar 

  28. W. C. Tai, Optimum design of a new tuned inerter-torsional-mass-damper passive vibration control for stochastically motion-excited structures, Journal of Vibration and Acoustics, 142(1) (2020) 1–9, DOI: https://doi.org/10.1115/1.4045264.

    Article  Google Scholar 

  29. H. C. Kwon, M. C. Kim and I.W. Lee, Vibration control of bridges under moving loads, Computers and Structures, 66(4) (1998) 473–480.

    Article  MATH  Google Scholar 

  30. B. W. Jo, G. H. Tae and D. W. Lee, Structural vibration of tuned mass damper-installed three-span steel box bridge, International Journal of Pressure Vessels and Piping, 78(10) (2001) 667–675, DOI: https://doi.org/10.1016/S0308-0161(01)00081-3.

    Article  Google Scholar 

  31. X. Yin, Y. Liu, G. Song and Y. L. Mo, Suppression of bridge vibration induced by moving vehicles using pounding tuned mass dampers, Journal of Bridge Engineering, 23(7) (2018) 1–14, DOI: https://doi.org/10.1061/(ASCE)BE.1943-5592.0001256.

    Article  Google Scholar 

Download references

Acknowledgments

We thank Stuart Jenkinson, Ph.D., from Edanz (https://jp.edanz.com/ac) for editing a draft of this manuscript.

Author information

Authors and Affiliations

  1. Faculty of Mechanical Engineering, Kyoto Institute of Technology, Kyoto, 6068585, Japan

    Nanako Miura & Naoki Matsuo

  2. Faculty of Geosciences and Civil Engineering, Kanazawa University, Ishikawa, 9201192, Japan

    Saiji Fukada

  3. Civil Engineering Division, Hazama Ando Corporation, Tokyo, 1078658, Japan

    Sawako Tomioka

Authors
  1. Nanako Miura
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Naoki Matsuo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Saiji Fukada
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Sawako Tomioka
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nanako Miura.

Additional information

Nanako Miura is an Associate Professor in the Faculty of Mechanical Engineering, Kyoto Institute of Technology, Kyoto, Japan. She received her Ph.D. in engineering from Keio University. Her research interests include vibration control, structural health monitoring, and earthquake disaster countermeasures.

Naoki Matsuo is a graduate student in the Faculty of Mechanical Engineering, Kyoto Institute of Technology, Kyoto, Japan. He received his B.Eng. from Kyoto Institute of Technology. His research interests include vibration control and vibration energy harvesting.

Saiji Fukada is a Professor in the Faculty of Geosciences and Civil Engineering, Kanazawa University, Ishikawa, Japan. He received his Doctor of Engineering degree from Kanazawa University. His research interests include bridge vibration, bridge maintenance, and structural health monitoring.

Sawako Tomioka is an engineer in the Civil and Structural Engineering Department, Civil Engineering Division, Hazama Ando Corporation, Tokyo, Japan. She received her Ph.D. in engineering from Waseda University. Her research interest includes bridge design.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Miura, N., Matsuo, N., Fukada, S. et al. Design and simulation of double-mass dynamic vibration absorber with residual vibration mode. J Mech Sci Technol 37, 2771–2779 (2023). https://doi.org/10.1007/s12206-023-0505-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-023-0505-7

Keywords

Search

Navigation