Skip to main content

Advertisement

Springer Nature Link
Log in

Knowledge Integration into deep learning in dynamical systems: an overview and taxonomy

  • Invited Review Article
  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

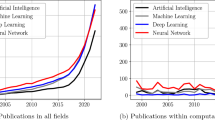
Abstract

Despite the sudden rise of AI, it still leaves a question mark to many newcomers on its widespread adoption as it exhibits a lack of robustness and interpretability. For instance, the insufficient amount of training data usually hinders its performance due to the lack of generalization, and the black box nature of deep neural networks does not allow for a precise explanation behind its mechanism preventing a new scientific discovery. Such limitations have led to the development of several branches of deep learning one of which include physics-informed neural networks that will be covered in the rest of this paper. In this overview, we defined the general concept of informed deep learning followed by an extensive literature survey in the field of dynamical systems. We hope to make a contribution to our mechanical engineering community by conveying knowledge and insights on this emerging field of study through this survey paper.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Abbreviations

θ s :

Source parameters

θ t :

Target parameters

f HPD :

Hybrid model

L PHY :

Physics-based loss

∅(k):

Convolution filter

a t :

Damage at time t

r n+1 :

Residual at n +1 step

References

  1. M. Reichstein, G. Camps-Valls, B. Stevens, M. Jung, J. Denzler and N. Carvalhais, Deep learning and process understanding for data-driven Earth system science, Nature, 566(7743) (2019) 195–204.

    Article  Google Scholar 

  2. Y. Yu, H. Yao and Y. Liu, Structural dynamics simulation using a novel physics-guided machine learning method, Engineering Applications of Artificial Intelligence, 96 (2020) 103947.

    Article  Google Scholar 

  3. A. Karpatne, W. Watkins, J. Read and V. Kumar, Physics-guided neural networks (pgnn): an application in lake temperature modeling, arXiv preprint arXiv:1710.11431 (2017).

  4. R. Zhang, Y. Liu and H. Sun, Physics-guided convolutional neural network (PhyCNN) for data-driven seismic response modeling, Engineering Structures, 215 (2020) 110704.

    Article  Google Scholar 

  5. X. Jia, J. Willard, A. Karpatne, J. Read, J. Zwart, M. Steinbach and V. Kumar, Physics guided RNNs for modeling dynamical systems: a case study in simulating lake temperature profiles, Proceedings of the 2019 SIAM International Conference on Data Mining, SIAM (2019) 558–566.

  6. M. A. Chao, B. T. Adey and O. Fink, Implicit supervision for fault detection and segmentation of emerging fault types with deep variational autoencoders, arXiv:1912.12502 (2020).

  7. R. Zhang, H. Tao, L. Wu and Y. Guan, Transfer learning with neural networks for bearing fault diagnosis in changing working conditions, IEEE Access, 5 (2017) 14347–14357.

    Article  Google Scholar 

  8. M. A. Chao, C. Kulkarni, K. Goebel and O. Fink, Fusing physics-based and deep learning models for prognostics, arXiv preprint arXiv:2003.00732 (2020).

  9. M. A. Chao, C. Kulkarni, K. Goebel and O. Fink, Hybrid deep fault detection and isolation: combining deep neural networks and system performance models, arXiv preprint arXiv:1908. 01529 (2019).

  10. J. Pfrommer, C. Zimmerling, J. Liu, L. Kärger, F. Henning and J. Beyerer, Optimisation of manufacturing process parameters using deep neural networks as surrogate models, Procedia CiRP, 72 (2018) 426–431.

    Article  Google Scholar 

  11. S. J. Leary, A. Bhaskar and A. J. Keane, A knowledge-based approach to response surface modelling in multifidelity optimization, Journal of Global Optimization, 26(3) (2003) 297–319.

    Article  MathSciNet  Google Scholar 

  12. M. Hipsey, L. Bruce and D. Hamilton, General Lake Model Overview and User Information, The University of Western Austrailia (2014).

  13. H. S. Kim, M. Koc and J. Ni, A hybrid multi-fidelity approach to the optimal design of warm forming processes using a knowledge-based artificial neural network, International Journal of Machine Tools and Manufacture, 47(2) (2007) 211–222.

    Article  Google Scholar 

  14. F. Wang and Q.-J. Zhang, Knowledge-based neural models for microwave design, IEEE Transactions on Microwave Theory and Techniques, 45(12) (1997) 2333–2343.

    Article  Google Scholar 

  15. F.-G. Yuan, S. A. Zargar, Q. Chen and S. Wang, Machine learning for structural health monitoring: challenges and opportunities, Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2020, International Society for Optics and Photonics (2020) 1137903.

  16. M. Raissi, P. Perdikaris and G. E. Karniadakis, Physics informed deep learning (part i): data-driven solutions of nonlinear partial differential equations, arXiv preprint arXiv:1711.10561 (2017).

  17. I. E. Lagaris, A. Likas and D. I. Fotiadis, Artificial neural networks for solving ordinary and partial differential equations, IEEE Transactions on Neural Networks, 9(5) (1998) 987–1000.

    Article  Google Scholar 

  18. S. Greydanus, M. Dzamba and J. Yosinski, Hamiltonian neural networks, Advances in Neural Information Processing Systems (2019) 15379–15389.

  19. N. Muralidhar, M. R. Islam, M. Marwah, A. Karpatne and N. Ramakrishnan, Incorporating prior domain knowledge into deep neural networks, 2018 IEEE International Conference on Big Data (Big Data), IEEE (2018) 36–45.

  20. R. Swischuk, L. Mainini, B. Peherstorfer and K. Willcox, Projection-based model reduction: formulations for physics-based machine learning, Computers & Fluids, 179 (2019) 704–717.

    Article  MathSciNet  Google Scholar 

  21. Y. Lu, M. Rajora, P. Zou and S. Y. Liang, Physics-embedded machine learning: case study with electrochemical micro-machining, Machines, 5(1) (2017) 4.

    Article  Google Scholar 

  22. C. Bauckhage, C. Ojeda, J. Schücker, R. Sifa and S. Wrobel, Informed machine learning through functional composition, LWDA (2018) 33–37.

  23. J. Ling, A. Kurzawski and J. Templeton, Reynolds averaged turbulence modelling using deep neural networks with embedded invariance, Journal of Fluid Mechanics, 807 (2016) 155–166.

    Article  MathSciNet  Google Scholar 

  24. C.-S. Huang, S.-L. Hung, C. Wen and T. Tu, A neural network approach for structural identification and diagnosis of a building from seismic response data, Earthquake Engineering & Structural Dynamics, 32(2) (2003) 187–206.

    Article  Google Scholar 

  25. A. Butter, G. Kasieczka, T. Plehn and M. Russell, Deep-learned top tagging with a Lorentz layer, SciPost Phys, 5(28) (2018) 1707.08966.

    Google Scholar 

  26. D. L. Bergman, Symmetry constrained machine learning, Proceedings of SAI Intelligent Systems Conference, Springer (2019) 501–512.

  27. M. Sadoughi and C. Hu, Physics-based convolutional neural network for fault diagnosis of rolling element bearings, IEEE Sensors Journal, 19(11) (2019) 4181–4192.

    Article  Google Scholar 

  28. B. Moaveni, J. P. Conte and F. M. Hemez, Uncertainty and sensitivity analysis of damage identification results obtained using finite element model updating, Computer-Aided Civil and Infrastructure Engineering, 24(5) (2009) 320–334.

    Article  Google Scholar 

  29. S. Yousefianmoghadam, I. Behmanesh, A. Stavridis, B. Moaveni, A. Nozari and A. Sacco, System identification and modeling of a dynamically tested and gradually damaged 10-story reinforced concrete building, Earthquake Engineering & Structural Dynamics, 47(1) (2018) 25–47.

    Article  Google Scholar 

  30. K. Hornik, Approximation capabilities of multilayer feedforward networks, Neural Networks, 4(2) (1991) 251–257.

    Article  MathSciNet  Google Scholar 

  31. C. Tianping and C. Hong, Approximations of continuous functions by neural networks with application to dynamic system, IEEE Transition Neural Networks, 4(6) (1993) 910–918.

    Article  Google Scholar 

  32. E. de Bezenac, A. Pajot and P. Gallinari, Deep learning for physical processes: incorporating prior scientific knowledge, Journal of Statistical Mechanics: Theory and Experiment, 2019(12) (2019) 124009.

    Article  MathSciNet  Google Scholar 

  33. Y. Zhu, N. Zabaras, P.-S. Koutsourelakis and P. Perdikaris, Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data, Journal of Computational Physics, 394 (2019) 56–81.

    Article  MathSciNet  Google Scholar 

  34. N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov, Dropout: a simple way to prevent neural networks from overfitting, The Journal of Machine Learning Research, 15(1) (2014) 1929–1958.

    MathSciNet  MATH  Google Scholar 

  35. R. King, O. Hennigh, A. Mohan and M. Chertkov, From deep to physics-informed learning of turbulence: diagnostics, arXiv preprint arXiv:1810.07785 (2018).

  36. Y. Du, Z. Liu, H. Basevi, A. Leonardis, B. Freeman, J. Tenenbaum and J. Wu, Learning to exploit stability for 3d scene parsing, Advances in Neural Information Processing Systems, 31 (2018) 1726–1736.

    Google Scholar 

  37. K.-H. Lee, G. Ros, J. Li and A. Gaidon, Spigan: Privileged adversarial learning from simulation, arXiv preprint arXiv:1810. 03756 (2018).

  38. A. Shrivastava, T. Pfister, O. Tuzel, J. Susskind, W. Wang and R. Webb, Learning from simulated and unsupervised images through adversarial training, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2017) 2107–2116.

  39. T. Cohen and M. Welling, Group equivariant convolutional networks, International Conference on Machine Learning (2016) 2990–2999.

  40. S. Dieleman, J. De Fauw and K. Kavukcuoglu, Exploiting cyclic symmetry in convolutional neural networks, arXiv preprint arXiv:1602.02660 (2016).

  41. J. Li, Z. Yang, H. Liu and D. Cai, Deep rotation equivariant network, Neurocomputing, 290 (2018) 26–33.

    Article  Google Scholar 

  42. D. E. Worrall, S. J. Garbin, D. Turmukhambetov and G. J. Brostow, Harmonic networks: deep translation and rotation equivariance, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2017) 5028–5037.

  43. R. G. Nascimento and F. A. Viana, Fleet prognosis with physics-informed recurrent neural networks, arXiv preprint arXiv: 1901.05512 (2019).

  44. A. Fatemi and L. Yang, Cumulative fatigue damage and life prediction theories: a survey of the state of the art for homogeneous materials, International Journal of Fatigue, 20(1) (1998) 9–34.

    Article  Google Scholar 

  45. D. M. Frangopol, M. J. Kallen and J. M. v. Noortwijk, Probabilistic models for life-cycle performance of deteriorating structures: review and future directions, Progress in Structural Engineering and Materials, 6(4) (2004) 197–212.

    Article  Google Scholar 

  46. A. Dourado and F. A. Viana, Physics-informed neural networks for corrosion-fatigue prognosis, Proceedings of the Annual Conference of the PHM Society (2019).

  47. A. D. Dourado and F. Viana, Physics-informed neural networks for bias compensation in corrosion-fatigue, AIAA Scitech 2020 Forum (2020) 1149.

  48. Y. Long, X. She and S. Mukhopadhyay, HybridNet: integrating model-based and data-driven learning to predict evolution of dynamical systems, arXiv preprint arXiv:1806.07439 (2018).

  49. M. Lutter, C. Ritter and J. Peters, Deep lagrangian networks: using physics as model prior for deep learning, arXiv preprint arXiv:1907.04490 (2019).

  50. J. N. Kani and A. H. Elsheikh, DR-RNN: A deep residual recurrent neural network for model reduction, arXiv preprint arXiv:1709.00939 (2017).

  51. J. Zhou, G. Cui, Z. Zhang, C. Yang, Z. Liu, L. Wang, C. Li and M. Sun, Graph neural networks: a review of methods and applications, arXiv preprint arXiv:1812.08434 (2018).

  52. A. Ortega, P. Frossard, J. Kovačević, J. M. Moura and P. Vandergheynst, Graph signal processing: overview, challenges, and applications, Proceedings of the IEEE, 106(5) (2018) 808–828.

    Article  Google Scholar 

  53. T. N. Kipf and M. Welling, Semi-supervised classification with graph convolutional networks, arXiv preprint arXiv:1609.02907 (2016).

  54. S. Seo and Y. Liu, Differentiable physics-informed graph networks, arXiv preprint arXiv:1902.02950 (2019).

  55. S. Seo, C. Meng and Y. Liu, Physics-aware difference graph networks for sparsely-observed dynamics, International Conference on Learning Representations (2019).

  56. G. Zhang, H. He and D. Katabi, Circuit-GNN: graph neural networks for distributed circuit design, International Conference on Machine Learning (2019) 7364–7373.

  57. A. Mojallal and S. Lotfifard, Multi-physics graphical modelbased fault detection and isolation in wind turbines, IEEE Transactions on Smart Grid, 9(6) (2017) 5599–5612.

    Article  Google Scholar 

  58. H. Khorasgani, A. Hasanzadeh, A. Farahat and C. Gupta, Fault detection and isolation in industrial networks using graph convolutional neural networks, 2019 IEEE International Conference on Prognostics and Health Management (ICPHM), IEEE (2019) 1–7.

  59. K. Chen, J. Hu, Y. Zhang, Z. Yu and J. He, Fault location in power distribution systems via deep graph convolutional networks, IEEE Journal on Selected Areas in Communications, 38(1) (2019) 119–131.

    Article  Google Scholar 

  60. Z. Gao, G. Lu and P. Yan, Graph-based change detection for condition monitoring of industrial machinery: an enhanced framework for non-stationary condition signals, Measurement Science and Technology, 30(11) (2019) 115002.

    Article  Google Scholar 

  61. T. Wang, G. Lu, J. Liu and P. Yan, Graph-based change detection for condition monitoring of rotating machines: techniques for graph similarity, IEEE Transactions on Reliability, 68(3) (2018) 1034–1049.

    Article  Google Scholar 

  62. D. P. Kingma and M. Welling, Auto-encoding variational bayes, arXiv preprint arXiv:1312.6114 (2013).

  63. I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville and Y. Bengio, Generative adversarial nets, Advances in Neural Information Processing Systems (2014) 2672–2680.

  64. J. E. Warner, J. Cuevas, G. F. Bomarito, P. E. Leser and W. P. Leser, Inverse estimation of elastic modulus using physics-informed generative adversarial networks, arXiv preprint arXiv: 2006.05791 (2020).

  65. L. Yang, D. Zhang and G. E. Karniadakis, Physics-informed generative adversarial networks for stochastic differential equations, SIAM Journal on Scientific Computing, 42(1) (2020) A292–A317.

    Article  MathSciNet  Google Scholar 

  66. I. Gulrajani, F. Ahmed, M. Arjovsky, V. Dumoulin and A. C. Courville, Improved training of wasserstein gans, Advances in Neural Information Processing Systems, 30 (2017) 5767–5777.

    Google Scholar 

  67. Y. Yang and P. Perdikaris, Physics-informed deep generative models, arXiv preprint arXiv:1812.03511 (2018).

  68. Y. Yang and P. Perdikaris, Adversarial uncertainty quantification in physics-informed neural networks, Journal of Computational Physics, 394 (2019) 136–152.

    Article  MathSciNet  Google Scholar 

  69. X. Jia, J. Zwart, J. Sadler, A. Appling, S. Oliver, S. Markstrom, J. Willard, S. Xu, M. Steinbach and J. Read, Physics-guided recurrent graph networks for predicting flow and temperature in river networks, arXiv preprint arXiv:2009.12575 (2020).

  70. V. H. Nguyen, J. S. Cheng, Y. Yu and V. T. Thai, An architecture of deep learning network based on ensemble empirical mode decomposition in precise identification of bearing vibration signal, Journal of Mechanical Science and Technology, 33(1) (2019) 41–50.

    Article  Google Scholar 

  71. F. de Avila Belbute-Peres, K. Smith, K. Allen, J. Tenenbaum and J. Z. Kolter, End-to-end differentiable physics for learning and control, Advances in Neural Information Processing Systems (2018) 7178–7189.

  72. A. S. Qureshi, A. Khan, A. Zameer and A. Usman, Wind power prediction using deep neural network based meta regression and transfer learning, Applied Soft Computing, 58 (2017) 742–755.

    Article  Google Scholar 

Download references

Acknowledgments

This work was partly supported by the National Research Foundation of Korea (NRF) grant funded by the Korea Government (MSIT) (No. 2020R1A2C1009744), Institute for Information & communications Technology Panning & Evaluation (IITP) grant funded by the Korea government (MSIP) (No. 2019-0-01906, Artificial Intelligence Graduate School Program (POSTECH)), the Institute of Civil Military Technology Cooperation funded by the Defense Acquisition Program Administration and Ministry of Trade, Industry and Energy of Korean government under grant No. 19-CM-GU-01, the Korea Institute of Energy Technology Evaluation and Planning (KETEP) Grant funded by the Korean Government (MOTIE) under Grant 20206610100290.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Pohang University of Science and Technology, 77 Cheongamro, Pohang, Korea

    Sung Wook Kim, Iljeok Kim, Jonghwan Lee & Seungchul Lee

  2. Graduate School of Artificial Intelligence, Pohang University of Science and Technology, 77 Cheongam-ro, Pohang, Korea

    Seungchul Lee

  3. Institute of Convergence Research and Education in Advanced Technology, Yonsei University, 50 Yonsei-ro, Seoul, Korea

    Seungchul Lee

Authors
  1. Sung Wook Kim
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Iljeok Kim
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jonghwan Lee
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Seungchul Lee
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Seungchul Lee.

Additional information

Recommended by Editor No-cheol Park

Sung Wook Kim received a B.S. degree in Mechanical Engineering from Hanyang University, Seoul, South Korea, in 2016. He then received his M.S. degree in Mechanical Engineering from Pohang University of Science and Technology, Pohang, South Korea, in 2018. He is now a Ph.D. candidate at the Industrial AI Lab. of Pohang University of Science and Technology. His research interests include industrial artificial intelligence with mechanical systems, and deep learning for smart manufacturing.

Iljeok Kim received a B.S. degree in Mechanical Engineering from Chungnam National University, Daejeon, South Korea, in 2017. He then received his M.S. degree in Mechanical Engineering from Pohang University of Science and Technology, Pohang, South Korea, in 2020. He is now a Ph.D. student at the Industrial AI Lab. of Pohang University of Science and Technology. His research interests include industrial artificial intelligence with mechanical systems, and deep learning for smart manufacturing.

Jonghwan Lee received a B.S. degree in Mechanical Engineering from Kyung-pook National University, Daegu, South Korea, in 2018. He is now a M.S. candidate at the Industrial AI Lab. of Pohang University of Science and Technology. His research interests include industrial artificial intelligence with mechanical systems, and deep learning for smart manufacturing.

Seungchul Lee received a B.S. degree from Seoul National University in 2001. He then received his M.S. and Ph.D. degrees from the University of Michigan, Ann Arbor, USA, in 2008, and 2010, respectively. He was an Assistant Professor with the Ulsan National Institute of Science and Technology, South Korea. He is currently an Assistant Professor at the Department of Mechanical Engineering at Pohang University of Science and Technology in Pohang, South Korea, since 2018. His research interests include industrial artificial intelligence with mechanical systems, deep learning for machine healthcare, and the IoT-based smart manufacturing.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kim, S.W., Kim, I., Lee, J. et al. Knowledge Integration into deep learning in dynamical systems: an overview and taxonomy. J Mech Sci Technol 35, 1331–1342 (2021). https://doi.org/10.1007/s12206-021-0342-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-021-0342-5

Keywords