Skip to main content
SpringerLink
Log in

A novel kriging based active learning method for structural reliability analysis

  • Original Article
  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

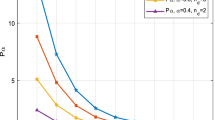
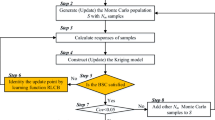
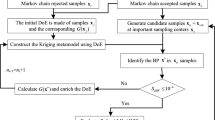
In the reliability analysis of engineering structures, there are usually implict and highly nonlinear performance function problems, which leads to the time-consuming computations. In this paper, a novel Kriging based reliability analysis method combined with the improved efficient global optimization (IEGO) and a secondary point selection strategy is proposed. Based on the IEGO algorithm, the expected improvement function is redefining, which will focus on the points both with large variance and near the limit state surface. Moreover, a secondary point selection strategy is raised to find the point with larger expected improvement and closed to the limit state surface, which can further improve the efficiency of the active learning process. Five examples indicates that the raised method has satisfactory global and local search capability, and can evaluate the probability of failure efficiently.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Y. T. Wu, Computational methods for efficient structural reliability and reliability sensitivity analysis, AIAA Journal, 32 (8) (1994) 1717–1723.

    Article  Google Scholar 

  2. S. K. Au, Reliability-based design sensitivity by efficient simulation, Computers & Structures, 83 (14) (2005) 1048–1061.

    Article  Google Scholar 

  3. C. Tong, Z. L. Sun and Q. L. Zhao, A hybrid algorithm for reliability analysis combining Kriging and subset simulation importance sampling, Journal of Mechanical Science and Technology, 29 (8) (2015) 3183–3193.

    Article  Google Scholar 

  4. B. Echard et al., A combined importance sampling and Kriging reliability method for small failure probabilities with timedemanding numerical models, Reliability Engineering and System Safety, 111 (8) (2013) 232–240.

    Article  Google Scholar 

  5. G. I. Schuller, H. J. Pradlwarter and P. S. Koutsourelakis, A critical appraisal of reliability estimation procedures for high dimensions, Probabilistic Engineering Mechanics, 19 (4) (2004) 463–473.

    Article  Google Scholar 

  6. J. Morio et al., A survey of rare event simulation methods for static input-output models, Simulation Modelling Practice and Theory, 49 (2014) 287–304.

    Article  Google Scholar 

  7. R. Rackwitz and B. Fiessler, Structural reliability under combined random load sequences, Computers & Structures, 9 (5) (1978) 489–494.

    Article  Google Scholar 

  8. F. F. Xiong et al., A double weighted stochastic response surface method for reliability analysis, Journal of Mechanical Science and Technology, 26 (8) (2012) 2573–2580.

    Article  Google Scholar 

  9. D. Q. Zhang et al., Time-dependent reliability analysis through response surface method, Journal of Mechanical Design, 139 (4) (2017) 041404.

    Article  Google Scholar 

  10. D. L. Allaix and V. I. Carbone. An improvement of the response surface method, Structural Safety, 33 (2) (2011) 165–172.

    Article  Google Scholar 

  11. H. Z. Dai et al., Structural reliability assessment by local approximation of limit state functions using adaptive markov chain simulation and support vector regression, Computer- Aided Civil and Infrastructure Engineering, 27 (9) (2012) 676–686.

    Article  Google Scholar 

  12. J. M. Bourinet, F. Deheeger and M. Lemaire, Assessing small failure probabilities by combined subset simulation and support vector machines, Structural Safety, 33 (6) (2011) 343–353.

    Article  Google Scholar 

  13. H. Z. Dai, H. Zhang and W. Wang, A support vector densitybased importance sampling for reliability assessment, Reliability Engineering & System Safety, 106 (2012) 86–93.

    Article  Google Scholar 

  14. J. Cheng et al., A new approach for solving inverse reliability problems with implicit response functions, Engineering Structures, 29 (1) (2007) 71–79.

    Article  Google Scholar 

  15. V. Papadopoulos et al., Accelerated subset simulation with neural networks for reliability analysis, Computer Methods in Applied Mechanics and Engineering, 223–224 (2012) 70–80.

    Article  MathSciNet  Google Scholar 

  16. G. B. Kingston et al., Computational intelligence methods for the efficient reliability analysis of complex flood defence structures, Structural Safety, 33 (1) (2011) 64–73.

    Article  Google Scholar 

  17. S. Choi, G. Lee and I. Lee, Adaptive single-loop reliabilitybased design optimization and post optimization using constraint boundary sampling, Journal of Mechanical Science and Technology, 32 (7) (2018) 3249–3262.

    Article  Google Scholar 

  18. S. Lee and J. H. Kim, An adaptive importance sampling method with a Kriging metamodel to calculate failure probability, Journal of Mechanical Science and Technology, 31 (12) (2017) 5769–5778.

    Article  Google Scholar 

  19. B. Echard, N. Gayton and M. Lemaire, AK-MCS: An active learning reliability method combining Kriging and Monte Carlo simulation, Structural Safety, 33 (2) (2011) 145–154.

    Article  Google Scholar 

  20. G. Matheron, The intrinsic random functions and their applications, Advances in Applied Probability, 5 (3) (1973) 439–468.

    Article  MathSciNet  Google Scholar 

  21. Z. Liu et al., Hybrid structure reliability method combining optimized Kriging model and importance sampling, Acta Aeronautica et Astronautica Sinica, 34 (6) (2013) 1347–1355.

    Google Scholar 

  22. J. Wei, J. G. Zhang and T. Qiu, Structural reliability algorithm based on improved dynamic Kriging model, Journal of Beijing University of Aeronautics and Astronautics, 45 (2) (2019) 373–380.

    Google Scholar 

  23. D. R. Jones, M. Schonlau and W. J. Welch, Efficient global optimization of expensive black-Box functions, Journal of Global Optimization, 13 (4) (1998) 455–492.

    Article  MathSciNet  Google Scholar 

  24. B. J. Bichon et al., Efficient global reliability analysis for nonlinear implicit performance functions, AIAA Journal, 46 (10) (2008) 2459–2468.

    Article  Google Scholar 

  25. Z. Y. Lv, Z. Z. Lu and P. Wang, A new learning function for Kriging and its application to solve reliability problems in engineering, Computers & Mathematics with Applications, 70 (5) (2015) 1182–1197.

    Article  MathSciNet  Google Scholar 

  26. M. Balesdent, J. Morio and J. Marzat, Kriging-based adaptive importance sampling algorithms for rare event estimation, Structural Safety, 44 (2334) (2013) 1–10.

    Article  Google Scholar 

  27. X. X. Huang, J. Q. Chen and H. P. Zhu, Assessing small failure probabilities by AK-SS: An active learning method combining Kriging and Subset simulation, Structural Safety, 59 (2016) 86–95.

    Article  Google Scholar 

  28. I. Depina et al., Reliability analysis with metamodel line sampling, Structural Safety, 60 (2016) 1–15.

    Article  Google Scholar 

  29. W. Y. Yun, Z. Z. Lu and X. Jiang, An efficient reliability analysis method combing adaptive Kriging and modified importance sampling for small failure probability, Structural and Multidisciplinary Optimization, 58 (2018) 1383–1393.

    Article  MathSciNet  Google Scholar 

  30. J. Sacks, S. B. Schiller and W. J. Welch, Design for computer experiment, Technometrics, 31 (1) (1989) 41–47.

    Article  MathSciNet  Google Scholar 

  31. H. L. Zhao et al., An efficient reliability method combining adaptive importance sampling and Kriging metamodel, Applied Mathematical Modelling, 39 (7) (2015) 1853–1866.

    Article  MathSciNet  Google Scholar 

  32. X. K. Yuan et al., A novel adaptive importance sampling algorithm based on Markov chain and low-discrepancy sequence, Aerospace Science and Technology, 29 (1) (2013) 253–261.

    Article  Google Scholar 

  33. Z. L. Sun et al., LIF: A new Kriging based learning function and its application to structural reliability analysis, Reliability Engineering & System Safety, 157 (2017) 152–165.

    Article  Google Scholar 

  34. F. Cadini, F. Santos and E. Zio, An improved adaptive Kriging-based importance technique for sampling multiple failure regions of low probability, Reliability Engineering & System Safety, 131 (8) (2014) 109–117.

    Article  Google Scholar 

  35. B. Keshtegar and Z. Meng, A hybrid relaxed first-order reliability method for efficient structural reliability analysis, Structural Safety, 66 (2017) 84–93.

    Article  Google Scholar 

  36. P. Wang, Z. Z. Lu and Z. C. Tang, An application of the Kriging method in global sensitivity analysis with parameter uncertainty, Applied Mathematical Modelling, 37 (9) (2013) 6543–6555.

    Article  MathSciNet  Google Scholar 

  37. W. Y. Yun et al., A novel step-wise AK-MCS method for efficient estimation of fuzzy failure probability under probability inputs and fuzzy state assumption, Engineering Structures, 183 (2019) 340–350.

    Article  Google Scholar 

  38. P. J. Zheng et al., A new active learning method based on the learning function U of the AK-MCS reliability analysis method, Engineering Structures, 148 (2017) 185–194.

    Article  Google Scholar 

Download references

Acknowledgments

The financial supports from the National Science and Technology Major Project of China (Grant No. 2017-V-0013-0065 and Grant No.2017-V-0010-0060) are gratefully acknowledged.

Author information

Authors and Affiliations

  1. School of Power and Energy, Northwestern Polytechnical University, Xi’an, 710072, China

    Hong Linxiong, Li Huacong, Peng Kai & Xiao Hongliang

Authors
  1. Hong Linxiong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Li Huacong
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Peng Kai
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xiao Hongliang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hong Linxiong.

Additional information

Recommended by Editor Chongdu Cho

Hong Linxiong is a Ph.D. candidate in the School of Power and Energy, Northwestern Polytechnical University. His research interests include structural reliability, aero-engine fuel system and others.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Linxiong, H., Huacong, L., Kai, P. et al. A novel kriging based active learning method for structural reliability analysis. J Mech Sci Technol 34, 1545–1556 (2020). https://doi.org/10.1007/s12206-020-0317-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-020-0317-y

Keywords

Search

Navigation