Dynamic analysis of rumor propagation model with media report and time delay on social networks

Abstract

When a rumor appears on social networks, the media of relevant departments need reaction time to make an authoritative announcement. Considering the effects of the media report and time delay on a rumor spreading, and the different attitudes of individuals towards media reports. We proposed a susceptible-expose-infective-media-remover (SEIMR) rumor propagation model with media reports and time delay. Firstly, the basic reproduction number of the model is obtained. Secondly, the positivity, boundedness and existence of the solutions of the model are analyzed. Then, the local asymptotic stability of the rumor free equilibrium and the boundary equilibriums is proved, and the global asymptotic stability of the equilibriums is proved by constructing Lyapunov function when the time delay is zero. Besides, the prevention and control effects of the media report on rumor spreading and the effect of time delay are analyzed. The shorter time delay in media report and the greater the impact of the media report, the more effective the suppression of rumors will be. Finally, the accuracy of the theoretical results as well as the effects of different parameters of the model have been verified through numerical simulations, and the effectiveness of the SEIMR model has been verified via comparative experiments.

1 Introduction

Rumors are statements that have no factual basis, but that are made up and spread through various means. Online social networks have become essential sources of information as the internet industry has grown, giving tremendous convenience to our daily lives. At the same time, rumors benefit from this as well. Unfortunately, rumors can disrupt our lives, provoke social panic, and even jeopardize national security. For example, since the epidemic of the COVID-19 outbreak, rumors about the virus and the COVID-19 vaccines have persisted unabated. The higher the immune response to the COVID-19 vaccine, the better the protective effectiveness; ivermectin, a veterinary medicine, is a “wonder drug” for the COVID-19 treatment; nucleic acid tests fail to detect the Delta virus and so on. Either alarmist or exaggerated, these rumors have become a stumbling block in the fight against the epidemic. Moreover, as the outbreak extended from Wuhan, rumors that the COVID-19 virus was a Chinese virus spread, and some overseas Chinese were treated unfairly. They were not allowed to enter specific places, and they were discriminated against even when they wore masks in public. Those rumors did bad harm to social stability and brought about bad effects on society. Therefore, how to effectively control rumor spreading on online social networks and establish an effective rumor spreading dynamic model is one of the hot issues at present [1].

The study of rumor spreading stems from the dynamics of infectious diseases, and the susceptible-infected-recovered (SIR) model [2] was the most classical infectious disease model. In 1965, the DK model [3] was proposed by Daley and Kendall, which was the most classic rumor propagation model. Subsequently, in 1973, Maki and Thomson proposed the MT model [4] based on the DK model, in which the authors considered the interaction between two rumor spreaders. Zanette [5, 6] first introduced complex network theory into rumor propagation research and studied rumor propagation on small-world networks and obtained the correlation between critical randomness and network connectivity. Nekovee and Morenno [7] derived the mean field equation to describe rumor propagation on complex networks, and the equation has been widely used in the subsequent study of teleological propagation dynamics based on complex networks.

Some scholars have considered the effects of forgetting mechanisms [8, 9] and memory mechanisms [10] on rumor spreading. Other studies considered the influence of individuals’ different attitudes toward rumors on rumor spreading [11,12,13]. Hu et al. [11] considered the effect of hesitant mechanism on rumor spreading and found that they have a positive impact on rumor spreading. Xia et al. [12] considered the individual hesitancy mechanism in consideration of the attractiveness and fuzziness of rumor content and conducted experimental simulations on artificial networks and real networks. By introducing the trust mechanism, Wang et al. [13] proposed a SIR model that divided ignorant people’s attitudes toward communicators into trust and distrust and calculated the probability of ignorant people being infected under different attitudes. In addition, there are also some scholars who study the law of rumor propagation based on information entropy theory and opinion dynamics [14,15,16]. Wang et al. [14] proposed an integrated model based on information entropy to investigate the effect of the role of memory, integration effects, differences in subjective tendencies to produce distortions and differences in the degree to which people trust each other on the spread of rumors. And then he [15] combined information distortion and polarization effects with a opinion dynamic model to investigate. Tan et al. [16] developed a model with the cross-issue solidarity and truth convergence.

Although the above research fully reveals the rules of rumor spreading, that study the spread of a single rumor without considering the influence of rumors refuting information.

As we all know, with the spread of rumors, there must be corresponding rumors refuting information or true information spread. Zhang et al. [17] added real information spreaders to rumor spreading and established a rumor spreading model, susceptible-infective-true-removed (SITR), considering people’s forgetting factors to rumors. Zan et al. [18] considered the influence of counterattacks on rumor spreading and established a susceptible-infective-counterattack-refractory (SICR) rumor spreading model. Zhang et al. [19] proposed that the complex competition mechanism between official-rumor-refuting-information (ORI) and rumors is the key to successful rumor refutation. Through the above research, the paper gain a new understanding and improve all aspects of rumor spreading.

However, much of the existing research was on static networks to study the spread of rumors and did not consider the inputs and outputs of the population [20,21,22,23]. In fact, the population of social networks changes dynamically according to the user’s registration rate and cancellation rate. Currently, there have been some studies on the influence of the dynamic evolution of the network on the transmission of infectious diseases and rumor spread [24,25,26,27,28,29,30], and affect of the network structure on rumor transmission process [31,32,33,34].

On the one hand, there are few studies on the impact of media reports on rumor spreading, and while some studies have studied the relationship between media reports and rumor spreading, they have not studied the dynamic effect. In particular, how media reports affect the transformational relationship between individuals remains unclear. In fact, if rumors spread on social networks, the media will carry out reports that refute rumors. When people choose to believe the media reports, some people may forward the information reported by the media, others will not forward the refute information, but will no longer believe rumors. Therefore, it is very important that our proposed model takes into account the role of media report in the transition mechanism between individuals. On the other hand, in the real world, authoritative media needs reaction time to make an authoritative announcement and clarify the rumor as the rumor starts to spread on social networks [35]. But few previous studies have studied the effects of media reports and time delay on rumors.

Based on the above analysis, the susceptible-expose-infective-media-remover (SEIMR) rumor spreading model is established on social network, which not only considers media reports and time-lag effects, but also considers how media reports affect the switching mechanism between individuals, especially the susceptible, the infective and the exposed are affected by media reports. The major work in the paper are as follows:

• 1. A new social network rumor propagation model with media report and time delay is proposed. The transition mechanism between individuals under media reports is considered.

• 2. The dynamic characteristics of the model are analyzed. The basic reproduction number and the equilibrium of the model are calculated, and the stability of the rumor free equilibrium and the boundary equilibrium is proved. And the global asymptotic stability of the equilibriums is proved by constructing Lyapunov function when the time delay is zero.

• 3. Simulation experiments are used to prove the theoretical results, the influence of important parameters on rumor propagation is analyzed, and the effectiveness of the model in this paper is verified by comparative experiments.

This paper is arranged as follows: In Sect. 2, a SEIMR rumor spreading model is proposed. In Sect. 3, the equilibrium and the basic reproduction number are calculated, and the stability of the SEIMR model is analyzed. In Sect. 4, some numerical simulations are given to verify the effectiveness of the theoretical results. Section 5 gives a brief summary to conclude this paper.

2 The SEIMR model formulation

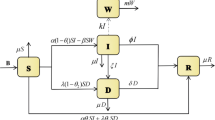
In this section, according to the characteristics of the propagation of rumors on social networks, all individuals fall into one of five categories. Susceptible (a person who has never heard of rumors), Infective (a person who heards rumors and spreads them), Expose (a person who heards rumors that does not spread them but will become the rumor carrier), Media (a authoritative media who heards the rumors but refuted them and make an authoritative announcement and clarify the rumor) and Remover (a person who knows rumors not believing and not spreading). The densities of susceptible, expose, infective, media, and remover are denoted by S(t), E(t), I(t), M(t), and R(t) at time t, respectively. N(t) represents the total number of the five categories at time t; here, $N(t)=S(t)+E(t)+I(t)+M(t)+R(t).$ In the SEIMR rumor propagation model, the conversion rules between individuals are as follows:

• 1. The number of social users will change dynamically over time when a new population is introduced or an old node is removed. Therefore, assume that the registration rate of social network users is rate A, and all new users are considered susceptible individuals; the cancellation rate of individuals in five categories is $\mu$.

• 2. The parameter $\tau$ is the lag between the rumors began to spread and the media of relevant departments make an authoritative announcement and clarify the rumor in real life.

• 3. Some studies have shown that the contact rate between individuals is affected by the density of each other, but we assume that the contact rate is a constant $\beta$ when a susceptible comes into contact with an infective. If the susceptible spreads rumors blindly with others without judgment, he/she will become infected at the rate $\alpha$; if the susceptible hears but does not spread the rumor, he/she will become exposed with rate $(1-\alpha )$. An exposed becomes an infective with the rate $\gamma$. An exposed becomes a remover with a recovery rate $\varepsilon$, and an infective becomes a remover with a recovery rate $\varepsilon$.

• 4. When a social network rumor appears, there will be many media reports about the positive information, and the rate of influence of media reports is $\delta$. When the susceptible contacts the media and hears the positive information, some of them will forward the positive information. After this behavior, we can assume that he/she has the attributes of a media. They become the media with a forward rate $\theta$, and others do not forward the positive information and become removers with a rate $(1-\theta )$. In the same way, the infected and the exposed become the media with a forward rate $\theta$, the infected and the exposed become the removers with a rate $(1-\theta )$.

• 5. The average degree of social network is $\bar{k}$, and all parameter range is between 0 and 1.

Based on the above assumptions, the status transfer process between different populations of rumor spread process is obtained, as shown in Fig. 1.

Fig. 1

Flow chart of rumor propagation under the influence of media report

According to the flow chart in Fig. 1, the Susceptible-Expose-Infective-Media-Remover (SEIMR) model of rumor propagation is established.

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{d S(t)}{dt}&{}=A-\beta \bar{k} S(t)I(t)-\delta \bar{k} S(t)M(t-\tau )-\mu S(t),\\ \frac{d E(t)}{dt}&{}=(1-\alpha )\beta \bar{k} S(t)I(t)-\delta \bar{k} E(t)M(t-\tau )- \gamma E(t)\\ &{}\quad -\varepsilon E(t)-\mu E(t),\\ \frac{d I(t)}{dt}&{}=\alpha \beta \bar{k} S(t)I(t)+\gamma E(t)-\delta \bar{k} I(t)M(t-\tau )-\varepsilon I(t)\\ &{}\quad -\mu I(t),\\ \frac{d M(t)}{dt}&{}=\delta \theta \bar{k} M(t-\tau )(S(t)+E(t)+I(t))-\mu M(t),\\ \frac{d R(t)}{dt}&{}=\delta (1-\theta ) \bar{k} M(t-\tau )(S(t)+E(t)+I(t))+\varepsilon E(t)\\ &{}\quad +\varepsilon I(t)-\mu R(t). \end{array}\right. \end{aligned}$$

(2.1)

With the initial conditions of the system(2.1) as following:

$$\begin{aligned} S(\varphi )= & {} \phi _1(\varphi ),\quad E(\varphi )=\phi _2(\varphi ),\quad I(\varphi )=\phi _3(\varphi ),\quad M(\varphi )=\phi _4(\varphi ),\quad R(t)=\phi _5(\varphi ),\nonumber \\ \phi= & {} (\phi _1, \phi _2, \phi _3, \phi _4, \phi _5)^\top \in B,\quad \phi _i(\varphi )\ge 0, \nonumber \\ \varphi\in & {} [-\tau ,0], \quad \phi _i(0)>0,\quad i=1,2,3,4,5. \end{aligned}$$

(2.2)

Where B denotes the Banach space of continuous mapping from the interval $[-\tau ,0]$ to $R^5$.

Because the first four equations of system (2.1) do not contain R(t), reduce (2.1) to the following system:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{d S(t)}{dt}=&{}A-\beta \bar{k} S(t)I(t)-\delta \bar{k} S(t)M(t-\tau )-\mu S(t),\\ \frac{d E(t)}{dt}=&{}(1-\alpha )\beta \bar{k} S(t)I(t)-\delta \bar{k} E(t)M(t-\tau )- \gamma E(t)\\ &{}-\varepsilon E(t)-\mu E(t),\\ \frac{d I(t)}{dt}=&{}\alpha \beta \bar{k} S(t)I(t)+\gamma E(t)-\delta \bar{k} I(t)M(t-\tau )-\varepsilon I(t)\\ &{}-\mu I(t),\\ \frac{d M(t)}{dt}=&{}\delta \theta \bar{k} M(t-\tau )(S(t)+E(t)+I(t))-\mu M(t),\\ \end{array} \right. \end{aligned}$$

(2.3)

Clearly, all of the solutions of system (2.3) are non-negative, which is compatible with the fact that in the actual life, the scale of the population evolution is non-negative.

3 The dynamics analysis for system (2.3)

In this section, we study the existence, positivity and boundedness of model solutions. And the basic reproduction number, the rumor-free equilibrium, boundary equilibrium, and positive equilibrium of rumor spreading on social network are calculated, and the stability of the equilibria are analyzed.

3.1 Positivity and boundedness

In order to prove the correctness of the model, we consider the positivity and boundedness of the solution of system (2.1).

Theorem 1

The solution of system (2.1) under initial condition (2.2) is positive for all $t\ge 0$.

Proof

As for the first equation of system (2.1), for $t\in [0,\tau ]$, namely, $t-\tau \in [-\tau ,0]$, according to the initial condition (2.2), we have

$$\begin{aligned} \frac{d S(t)}{dt}= & {} A-\beta \bar{k} S(t)I(t)-\delta \bar{k} S(t)M(t-\tau )-\mu S(t)\\\ge & {} -\beta \bar{k} S(t) I(t)-\delta \bar{k}S(t) M(t-\tau )-\mu S(t). \end{aligned}$$

Then we can obtain

$$\begin{aligned} S(t)\ge S(0)e^{\int _0^{t}(-\beta \bar{k}I(t)-\delta \bar{k}M(t-\varphi )- \mu )d\varphi }>0, \end{aligned}$$

for all $t\in [0,\tau ]$. By the method of induction, we make a recursive argument on $[\tau ,2\tau ], [2\tau ,3\tau ]\ldots$, and then obtain that $S(t)>0$ for all $t\ge 0$.

The following equations can be obtained separately using the same method

$$\begin{aligned} \begin{array}{ll} \frac{d E(t)}{dt}&{}=(1-\alpha )\beta \bar{k} S(t)I(t)-\delta \bar{k} E(t)M(t-\tau )- \gamma E(t)-\varepsilon E(t)-\mu E(t)\\ &{}\ge -\delta \bar{k} E(t)M(t-\tau )- \gamma E(t)-\varepsilon E(t)-\mu E(t),\\ \frac{d I(t)}{dt}&{}=\alpha \beta \bar{k} S(t)I(t)+\gamma E(t)-\delta \bar{k} I(t)M(t-\tau )-\varepsilon I(t)-\mu I(t)\\ &{}\ge -\delta \bar{k} I(t)M(t-\tau )-\varepsilon I(t)-\mu I(t),\\ \frac{d M(t)}{dt}&{}=\delta \theta \bar{k} M(t-\tau )(S(t)+E(t)+I(t))-\mu M(t)\\ &{}\ge -\mu M(t),\\ \frac{d R(t)}{dt}&{}=\delta (1-\theta ) \bar{k} M(t-\tau )(S(t)+E(t)+I(t))+\varepsilon E(t)+\varepsilon I(t)-\mu R(t)\\ &{}\ge -\mu R(t). \end{array} \end{aligned}$$

Integrating the above equations separately yields:

$$\begin{aligned} E(t)\ge & {} E(0)e^{\int _0^{t}(-\delta \bar{k} M(t-\varphi )- \gamma -\varepsilon -\mu )d\varphi }>0,\\ I(t)\ge & {} I(0)e^{\int _0^{t}(-\delta \bar{k}M(t-\varphi )-\varepsilon -\mu )d\varphi }>0,\\ M(t)\ge & {} M(0)e^{-\mu t}>0,\\ R(t)\ge & {} R(0)e^{-\mu t}>0. \end{aligned}$$

To sum up, the Theorem 1 is proven. $\square$

Theorem 2

The solution of system (2.1) under initial condition (2.2) is bounded i.e., there is a positively invariant set for (2.1).

Proof

We assume that (S(t), E(t), I(t), M(t), R(t)) is a solution with the initial condition. Let $S(t)+E(t)+I(t)+M(t)+R(t)=N(t)$. From the five equation of system (2.1), we can obtain: that the total population N(t) of the network satisfies the following equation:

$$\begin{aligned} \frac{d N(t)}{dt}=A-\mu N(t). \end{aligned}$$

(3.1)

To solve Eq. (3.1), $N(t)=(N_0-1)e^{-\mu t}+\frac{A}{\mu }$, and $N(0)=S(0)+E(0)+I(0)+M(0)+R(0)$, represents the total number individuals of the five categories at the initial moment. Thus, we have

$$\begin{aligned} \lim \limits _{t \rightarrow +\infty } N(t)=\frac{A}{\mu }. \end{aligned}$$

(3.2)

Hence, all solutions S(t), E(t), I(t), M(t), and R(t) are bounded by $\frac{A}{\mu }$. Thus, every forward variable orbit of system (2.1) eventually enters

$$\begin{aligned} D= & {} \Big \{(S(t), E(t), I(t), M(t), R(t))\in R_+^5|0 \nonumber \\{} & {} \le S(t)+E(t)+I(t)+M(t)+R(t) \le \frac{A}{\mu }\Big \}. \end{aligned}$$

(3.3)

And D is positively invariant. $\square$

3.2 Existence of the equilibria

This part will calculate equilibria of the SEIMR model. Let the right end of system (2.3) be zero.

When $I(t)=0$, $M(t)=0$ the rumor free equilibrium $E_0$ is obtained. When $I(t)=0$, $M(t)\ne 0$ the boundary equilibrium $E_1$ is obtained. And when $I\ne 0$, $M=0$ the boundary equilibrium $E_2$ is obtained. When $I(t)\ne 0, M(t)\ne 0$. the positive equilibrium $E_3^*$ is obtained.

Where

$$\begin{aligned} E_0= & {} \left( \frac{A}{\mu }, 0, 0, 0\right) ,\quad E_1=\left( \frac{\mu }{\delta \theta \bar{k}}, 0, 0, \frac{\mu (R_2-1)}{\delta \bar{k}} \right) ,\\ E_2= & {} \left( \frac{A}{\mu R_1}, \frac{A(1-\alpha )(R_1-1)}{(\varepsilon +\mu +\gamma )R_1}, \frac{\mu (R_1-1)}{\beta \bar{k}}, 0\right) . \end{aligned}$$

Next, the existence of the positive equilibrium $E_3^*=(S^*,E^*,I^*,M^*)$ will be introduced in detail.

Set $I(t)\ne 0, M(t)\ne 0$, and then $E^*, I^*,$ $M^*$ can be represented by variable $S^*$. Where

$$\begin{aligned} E^*= & {} \frac{(\delta \theta \varepsilon (A\bar{k}\delta \theta \varepsilon +\mu \varepsilon +\mu \gamma )-\beta \mu (A\bar{k}\delta \theta +\alpha \mu \varepsilon +\mu \gamma ))S^* +\delta \theta A(A\bar{k}\delta \theta +\mu \gamma +\mu \varepsilon )+A\beta \mu ^2(1-\alpha )}{\mu \beta (\delta \theta A\bar{k}+\mu \gamma )}, \end{aligned}$$

$$\begin{aligned} I^*= & {} \frac{\mu \gamma (\delta \theta \bar{k}S^*-\mu )}{\delta \theta \bar{k}((\bar{k}\alpha \beta \mu -\delta \theta \bar{k}\varepsilon )S^*-\delta \theta A\bar{k}-\mu \gamma )}, \\ M^*= & {} \frac{\delta \theta \bar{k}\varepsilon S^*+\delta \theta A \bar{k}-\mu ^2-\mu \varepsilon }{\mu \delta \bar{k}}. \end{aligned}$$

And variable $S^*$ satisfy the following equation:

$$\begin{aligned} q_2S^{*2}+q_1S^*+q_0=0, \end{aligned}$$

(3.4)

where

$$\begin{aligned} q_2= & {} \bar{k}\alpha \beta \delta \mu \theta \varepsilon -\bar{k}\delta ^2\theta ^2\varepsilon ^2,\\ q_1= & {} A\bar{k}\alpha \beta \delta \mu \theta -2A\bar{k}\delta ^2\theta ^2\varepsilon -\delta \gamma \mu \theta \varepsilon +\beta \gamma \mu ^2,\\ q_0= & {} -A^2\bar{k}\delta ^2\theta ^2-A\delta \gamma \mu \theta . \end{aligned}$$

The discriminant of Eq. (3.4) is $\Delta =A^2\bar{k}^2\alpha ^2\beta ^2\delta ^2\mu ^2\theta ^2+$ $2A\bar{k}\alpha \beta \delta ^2\gamma \mu ^2\theta ^2\varepsilon +2A\bar{k}\alpha \beta ^2\delta \gamma \mu ^3\theta$ $-4A\bar{k}\beta \delta ^2\gamma \mu ^2\theta ^2\varepsilon +(\delta \gamma \mu \theta \varepsilon -\beta \gamma \mu ^2)^2.$ The existence of positive roots of Eq. (3.4) is discussed in the following cases.

Case 1: When $\frac{\alpha \beta \mu }{\delta \theta \varepsilon }>1$, then $q_2>0$. Because $q_0<0$, then $\Delta >0$, thus, Eq. (3.4) has a unique positive root $S_{31}^*$, system (2.3) has a positive equilibrium $E_{3}^*=(S_{31}^*, E_{31}^*, I_{31}^*, M_{31}^*)$.

Case 2: When $\frac{\alpha \beta \mu }{\delta \theta \varepsilon }<1$, then $q_2<0$. When $\frac{A\bar{k}\alpha \beta \delta \mu \theta +\beta \gamma \mu ^2}{2A\bar{k}\delta ^2\theta ^2\varepsilon +\delta \gamma \mu \theta \varepsilon }>1$, then $q_1>0$. And when $\Delta >0$, Eq. (3.4) has two unique positive roots $S_{41}^*$ and $S_{51}^*$, system (2.3) has two positive equilibrium $E_{4}^*=(S_{41}^*, E_{41}^*, I_{41}^*, M_{41}^*)$, and $E_{5}^*=(S_{51}^*, E_{51}^*, I_{51}^*, M_{51}^*)$.

3.3 Basic reproduction number

To calculate the basic reproduction number of system (2.3), we consider it without delay. So, we have:

$$\begin{aligned} \begin{array}{ll} f_1=A-\beta \bar{k} S(t)I(t)-\delta \bar{k} S(t)M(t)-\mu S(t),\\ f_2=(1-\alpha )\beta \bar{k} S(t)I(t)-\delta \bar{k} E(t)M(t)- \gamma E(t)-\varepsilon E(t)-\mu E(t),\\ f_3=\alpha \beta \bar{k} S(t)I(t)+\gamma E(t)-\delta \bar{k} I(t)M(t)-\varepsilon I(t)-\mu I(t),\\ f_4=\delta \theta \bar{k} M(t)(S(t)+E(t)+I(t))-\mu M(t),\\ \end{array} \end{aligned}$$

Next, the basic reproduction number $R_0$ is calculated by using the next-generation matrix method [36, 37].

$$\begin{aligned} {{\mathscr {F}}(X)}= & {} \left( \begin{array}{ccc} \alpha \beta \bar{k} S(t)I(t)\\ (1-\alpha )\beta \bar{k} S(t)I(t) \\ \delta \theta \bar{k} M(t)S(t)\\ \end{array}\right) ,\\ {{\mathscr {V}}(X)}= & {} \left( \begin{array}{ccc} -\gamma E(t)+\delta \bar{k} I(t)M(t)+\varepsilon I(t)+\mu I(t)\\ \delta \bar{k} E(t)M(t)+ \gamma E(t)+\varepsilon E(t)+\mu E(t) \\ -\delta \theta \bar{k} M(t)(E(t)+I(t))+\mu M(t) \end{array} \right) . \end{aligned}$$

Then, the Jacobin Matrix of F(X) and V(X) are obtained at equilibrium $E_0$.

$$\begin{aligned} {F(E_0)}= & {} \left( \begin{array}{ccc} \alpha \beta \bar{k} \frac{A}{\mu } &{} 0 &{} 0\\ (1-\alpha )\beta \bar{k} \frac{A}{\mu }&{} 0 &{} 0\\ 0 &{} 0 &{} \delta \theta \bar{k}\frac{A}{\mu }\\ \end{array} \right) ,\\ {V(E_0)}= & {} \left( \begin{array}{ccc} \varepsilon +\mu &{} -\gamma &{} 0\\ 0 &{} \varepsilon +\mu +\gamma &{} 0 \\ 0 &{} 0 &{} \mu \\ \end{array} \right) . \end{aligned}$$

Thus, ${FV^{-1}}$ can be calculated as follows:

$$\begin{aligned} {FV^{-1}}= \left( \begin{array}{ccc} \frac{\alpha \beta A\bar{k}}{\mu (\varepsilon +\mu )} &{} \frac{\alpha \beta A\bar{k}\gamma }{\mu (\varepsilon +\mu )(\varepsilon +\mu +\gamma )} &{} 0\\ \frac{(1-\alpha ) \beta A\bar{k}}{\mu (\varepsilon +\mu )} &{} \frac{(1-\alpha ) \beta A\bar{k}\gamma }{\mu (\varepsilon +\mu )(\varepsilon +\mu +\gamma )} &{} 0 \\ 0 &{} 0 &{} \frac{\delta \theta A \bar{k}}{\mu ^2} \end{array}\right) , \end{aligned}$$

The maximum spectral radius of $FV^{-1}$ is the basic reproduction number of system (2.3), ie.,

$$\begin{aligned} R_0=\max \{\rho (FV^{-1})\}=\max \{R_1,R_2\}, \end{aligned}$$

where $R_1=\frac{\beta A\bar{k}(\alpha \mu +\alpha \varepsilon +\gamma )}{\mu (\varepsilon +\mu )(\varepsilon +\mu +\gamma )}$, and $R_2=\frac{\delta \theta A \bar{k}}{\mu ^2}.$

3.4 The local asymptotic stability of the equilibria

In this section, we prove the local asymptotic stability of the rumor free equilibrium $E_0$, the boundary equilibriums $E_1$ and $E_2$.

Theorem 3

The rumor free equilibrium $E_0$ of system (2.3) is locally asymptotically stable for $\tau \ge 0$ when $R_0<1$.

Proof

The Jacobian matrix of system (2.3) at the rumor free equilibrium $E_0$ is obtained as follows:

$$\begin{aligned} {J(E_0)}= \left( \begin{array}{cccc} -\mu &{} 0 &{} - \frac{\beta A \bar{k}}{\mu } &{} \frac{\delta A \bar{k}}{\mu }e^{-\lambda \tau }\\ 0 &{} -\varepsilon -\mu -\gamma &{} \frac{(1-\alpha )\beta A \bar{k}}{\mu } &{} 0 \\ 0 &{} \gamma &{} \frac{\alpha \beta A \bar{k}}{\mu }-\varepsilon -\mu &{} 0\\ 0 &{} 0 &{} 0 &{} \mu R_2 e^{-\lambda \tau } -\mu \end{array} \right) . \end{aligned}$$

Then, according to $|\lambda E-J(E_0)|$, there is obtained the corresponding characteristic equation:

$$\begin{aligned} (\lambda +\mu )(\lambda ^2+c_1\lambda +c_0)(\lambda -\mu R_2e^{-\lambda \tau }+\mu )=0, \end{aligned}$$

(3.5)

where $c_1=(\varepsilon +\mu )\left( 1-\frac{\alpha \beta A \bar{k}}{\mu (\varepsilon +\mu )}\right) +\varepsilon +\mu +\gamma$, $c_0=(\varepsilon +\mu +\gamma )(\varepsilon +\mu )(1-R_1)$.

Obviously, two eigenvalues of the characteristic equation are $\lambda _{01}=-\mu$, and $\lambda _{02}$ is the root of the equation $\lambda -\mu R_2e^{-\lambda \tau } +\mu =0$, and the other eigenvalues satisfy the equation as follows:

$$\begin{aligned} \lambda ^2+c_1\lambda +c_0=0. \end{aligned}$$

(3.6)

If $R_1<1$, ie., $R_1=\frac{\beta A\bar{k}(\alpha \mu +\alpha \varepsilon +\gamma )}{\mu (\varepsilon +\mu )(\varepsilon +\mu +\gamma )}<1$, thus $c_1>0, c_0>0$. Namely, both roots of Eq. (3.6) have negative real parts.

When $\tau =0,$ we have $\lambda _{02}=\mu (R_2 -1)$, if $R_2<1$, then $\lambda _{02}<0$. According to the Routh–Hurwitz stability criterion, the rumor free equilibrium $E_0$ of system (2.3) is locally asymptotically stable.

When $\tau >0,$ assuming that $\lambda =i\omega ,$ then

$$\begin{aligned} \left\{ \begin{array}{ll} \omega =-\mu R_2 \sin \omega \tau ,\\ \mu = \mu R_2 \cos \omega \tau .\\ \end{array} \right. \end{aligned}$$

(3.7)

By squaring both sides of Eq. (3.7) and adding them up, the following equations exist

$$\begin{aligned} \omega ^2=\mu ^2(R_2^2-1). \end{aligned}$$

(3.8)

If $R_2<1$, then $\mu ^2(R_2^2-1)<0$. This indicates that there are no positive real roots $\omega$ to satisfy Eq. (3.8). Therefore, the equilibrium $E_0$ of system (2.3) is locally asymptotically stable, and Theorem 3 is proven. $\square$

Theorem 4

The equilibrium $E_1$ of system (2.3) is locally asymptotically stable for $\tau \ge 0$ when $R_2>1$ and $\beta <\frac{\delta \theta (\delta \theta A \bar{k}+\mu \varepsilon )(\delta \theta A \bar{k}+\mu \varepsilon +\mu \gamma )}{\mu ^2(\delta \theta A \bar{k}\alpha +\alpha \varepsilon \mu +\gamma \mu )}$.

Proof

The Jacobian matrix of system (2.3) at the equilibrium $E_1$ is obtained as follows:

$$\begin{aligned} {J(E_1)}= \left( \begin{array}{cccc} -\mu R_2 &{} 0 &{} - \frac{\beta \mu }{\delta \theta } &{} -\frac{\mu }{\theta }e^{-\lambda \tau }\\ 0 &{} -\mu R_2-\gamma -\varepsilon &{} \frac{(1-\alpha )\beta \mu }{\delta \theta } &{} 0 \\ 0 &{} \gamma &{} \frac{\alpha \beta \mu }{\delta \theta }-\mu R_2-\varepsilon &{} 0\\ \mu \theta (R_2-1) &{} \mu \theta (R_2-1) &{} \mu \theta (R_2-1) &{} \mu e^{-\lambda \tau }-\mu \end{array} \right) , \end{aligned}$$

Construct a corresponding characteristic equation:

$$\begin{aligned} (\lambda ^2+p_1\lambda +p_0)(\lambda ^2+(\mu R_2+\mu -\mu e^{-\lambda \tau })\lambda +\mu ^2(R_2-e^{-\lambda \tau }))=0, \end{aligned}$$

(3.9)

where $p_1=2\frac{\delta \theta A \bar{k}}{\mu }+\gamma +2\varepsilon -\frac{\alpha \beta \mu }{\delta \theta },$

$$\begin{aligned} p_0= & {} \left( \frac{\delta \theta A \bar{k}}{\mu }\right) ^2+\frac{\delta \theta A \bar{k}\gamma }{\mu }+\frac{2\delta \theta A \bar{k} \varepsilon }{\mu }+\gamma \varepsilon +\varepsilon ^2\\{} & {} -\frac{A \bar{k}\alpha \beta \delta \theta +\alpha \beta \mu \varepsilon +\beta \gamma \mu }{\delta \theta }. \end{aligned}$$

Obviously, two eigenvalues of the characteristic equation are satisfy the equation as follows:

$$\begin{aligned} \lambda ^2+p_1\lambda +p_0=0, \end{aligned}$$

(3.10)

the other eigenvalues satisfy the following equation:

$$\begin{aligned} \lambda ^2+(\mu R_2+\mu -\mu e^{-\lambda \tau })\lambda +\mu ^2(R_2-e^{-\lambda \tau })=0. \end{aligned}$$

(3.11)

If $\beta <\frac{\delta \theta (\delta \theta A \bar{k}+\mu \varepsilon )(\delta \theta A \bar{k}+\mu \varepsilon +\mu \gamma )}{\mu ^2(\delta \theta A \bar{k}\alpha +\alpha \varepsilon \mu +\gamma \mu )}$, then $p_0>0$, and $p_1>0$. The eigenvalues of the characteristic Eq. (3.10) have negative real parts.

When $\tau =0,$ then the Eq. (3.11) can be simplified as follows:

$$\begin{aligned} \lambda ^2+\mu R_2 \lambda +\mu ^2 (R_2 -1)=0. \end{aligned}$$

(3.12)

If $R_2>1$, then $\mu ^2(R_2-1)>0$. The eigenvalues of the characteristic Eq. (3.12) have negative real parts. All eigenvalues of Eq. (3.9) have negative real parts, the equilibrium $E_1$ of system (2.3) is locally asymptotically stable.

When $\tau >0,$ assuming that $\lambda =i\omega (\omega >0)$. According to Eq. (3.11), we can obtain

$$\begin{aligned} \left\{ \begin{array}{ll} \omega ^2-\mu ^2 R_2=-\mu \omega \sin \omega \tau - \mu ^2\cos \omega \tau ,\\ (\mu R_2+\mu )\omega =\mu \omega \cos \omega \tau - \mu ^2\sin \omega \tau .\\ \end{array} \right. \end{aligned}$$

(3.13)

Squaring and adding the two equations of Eq. (3.13), then we can obtain

$$\begin{aligned} \omega ^4+\mu ^2R_2^2\omega ^2+\mu ^4(R_2^2-1)=0, \end{aligned}$$

(3.14)

assuming that $z=\omega ^2,$ then we can obtain

$$\begin{aligned} z^2+\mu ^2R_2^2z+\mu ^4(R_2^2-1)=0. \end{aligned}$$

(3.15)

If $R_2>1$, then $\mu ^4(R_2^2-1)>0$, thus, there are no any positive roots for Eq. (3.15). That is to say, there are no positive roots for Eq. (3.11). The equilibrium $E_1$ of system (2.3) is locally asymptotically stable, and Theorem 4 is proven. $\square$

Theorem 5

The equilibrium $E_2$ of system (2.3) is locally asymptotically stable for $\tau \ge 0$ when $R_1>1$, and $R_2<\frac{\beta A\bar{k}(\varepsilon +\mu +\gamma )R_1}{(\varepsilon +\mu +\gamma )\beta A\bar{k}+\mu ^2 R_1(R_1-1)+\mu \beta A\bar{k}(1-\alpha )(R_1-1)}$.

Proof

The Jacobian matrix of system (2.3) at the equilibrium $E_2$ is obtained as follows:

$$\begin{aligned} {J(E_2)}= \left( \begin{array}{cccc} \frac{-\beta \bar{k}A(1-\alpha )(R_1-1)}{(\varepsilon +\mu +\gamma )R_1}-\mu &{} 0 &{} \frac{-\beta \bar{k}A}{\mu R_1} &{} \frac{-\delta \bar{k}A}{\mu R_1}e^{-\lambda \tau }\\ \frac{(1-\alpha )\beta \bar{k}A(1-\alpha )(R_1-1)}{(\varepsilon +\mu +\gamma )R_1} &{} -\mu -\gamma -\varepsilon &{} \frac{(1-\alpha )\beta \bar{k}A}{\mu R_1} &{} \frac{-\delta \bar{k}\mu (R_1-1)}{\beta \bar{k}}e^{-\lambda \tau } \\ \frac{\alpha \beta \bar{k}A(1-\alpha )(R_1-1)}{(\varepsilon +\mu +\gamma )R_1} &{} \gamma &{} \frac{\alpha \beta \bar{k}A}{\mu R_1}-\varepsilon -\mu &{} \frac{-\delta \bar{k}A(1-\alpha )(R_1-1)}{(\varepsilon +\mu +\gamma )R_1}e^{-\lambda \tau }\\ 0 &{} 0 &{} 0 &{} {\delta \theta \bar{k}e^{-\lambda \tau }\eta -\mu } \end{array} \right) , \end{aligned}$$

Construct a characteristic equation:

$$\begin{aligned} (\lambda -\delta \theta \bar{k}\eta e^{-\lambda \tau }+\mu )(\lambda ^3+b_2\lambda ^2+b_1\lambda +b_0)=0, \end{aligned}$$

(3.16)

One of the characteristic roots of Eq. (3.16) is $\lambda _{21}=\delta \theta \bar{k}\eta e^{-\lambda \tau }-\mu$, where

$$\begin{aligned} \begin{aligned} \eta =\frac{(\varepsilon +\mu +\gamma )(\beta A\bar{k}+\mu ^2(R_1-1)R_1)+\beta \bar{k}\mu A (1-\alpha )(R_1-1)}{\beta \bar{k}\mu (\varepsilon +\mu +\gamma )R_1}. \end{aligned} \end{aligned}$$

The rest of the characteristic roots satisfy the equation:

$$\begin{aligned} \lambda ^3+b_2\lambda ^2+b_1\lambda +b_0=0, \end{aligned}$$

(3.17)

where

$$\begin{aligned} b_2= & {} (\varepsilon +\mu )\left( 1-\frac{W}{R_1}\right) +(\varepsilon +\mu +\gamma )+\mu R_1,\\ b_1= & {} \mu (\varepsilon +\mu )\left( R_1-\frac{W}{R_1}\right) +\mu (\varepsilon +\mu +\gamma )R_1,\\ b_0= & {} \mu (\varepsilon +\mu )(\varepsilon +\mu +\gamma )(R_1-1),\\ W= & {} \frac{\alpha \beta A \bar{k}}{\mu (\varepsilon +\mu )}. \end{aligned}$$

Then,

$$\begin{aligned} \Delta _1= & {} b_2=(\varepsilon +\mu )\left( 1-\frac{W}{R_1}\right) +(\varepsilon +\mu +\gamma )+\mu R_1,\\ {\Delta _2}= & {} \bigg |\begin{array}{ccc} b_2 &{} 1 \\ b_0 &{} b_1 \end{array} \bigg |=b_2 b_1 -b_0=(\varepsilon +\mu )^2\left( 1-\frac{W}{R_1}\right) \left( R_1-\frac{W}{R_1}\right) \\{} & {} +\mu (\varepsilon +\mu )(\varepsilon +\mu +\gamma )(\varepsilon +\mu +\gamma )(R_1-W)\\{} & {} +\mu (\varepsilon +\mu +\gamma )^2R_1+\mu ^2(\varepsilon +\mu )(R_1^2-W)+\mu ^2(\varepsilon +\mu +\gamma )R_1^2\\{} & {} +\mu (\varepsilon +\mu )(\varepsilon +\mu +\gamma )\left( 1-\frac{W}{R_1}\right) . \end{aligned}$$

According to the Routh–Hurwitz stability criterion, if $R_1>1$, then $W=\frac{\alpha \beta A \bar{k}}{\mu (\varepsilon +\mu )}<R_1$, thus $b_2>0, b_1>0$ and $b_0>0$, and further $\Delta _1>0$ and $\Delta _2>0$ hold. Thus, there are no any positive roots for Eq. (3.17).

When $\tau =0,$ if $R_2<\frac{\beta A\bar{k}(\varepsilon +\mu +\gamma )R_1}{(\varepsilon +\mu +\gamma )\beta A\bar{k}+\mu ^2 R_1(R_1-1)+\mu \beta A\bar{k}(1-\alpha )(R_1-1)}$, then $\lambda _{21}=\delta \theta \bar{k}\eta -\mu <0$ Thus, there are no any positive roots for Eq. (3.16). The equilibrium $E_2$ of system (2.3) is locally asymptotically stable.

When $\tau >0,$ assuming that $\lambda _{21}=i\omega (\omega >0)$, then

$$\begin{aligned} \left\{ \begin{array}{ll} \omega =-\delta \theta \bar{k}\eta \sin \omega \tau ,\\ \mu =\delta \theta \bar{k}\eta \cos \omega \tau .\\ \end{array} \right. \end{aligned}$$

(3.18)

By squaring both sides of Eq. (3.18), and adding them up, the following equations exist:

$$\begin{aligned} \omega ^2=\mu ^2\left( \left( \frac{\delta \theta \bar{k}\eta }{\mu }\right) ^2-1\right) . \end{aligned}$$

(3.19)

If $R_2<\frac{\beta A\bar{k}(\varepsilon +\mu +\gamma )R_1}{(\varepsilon +\mu +\gamma )\beta A\bar{k}+\mu ^2 R_1(R_1-1)+\mu \beta A\bar{k}(1-\alpha )(R_1-1)}$, we have $\frac{\delta \theta \bar{k}\eta }{\mu }<1$, then $\left( \frac{\delta \theta \bar{k}\eta }{\mu }\right) ^2-1<1$. Thus, there is Eq. (3.19) has no positive roots, namely, $\lambda _{21}$ is a constant negative. Thus, the equilibrium $E_2$ of system (2.3) is locally asymptotically stable, and Theorem 5 is proven. $\square$

3.5 The globally asymptotic stability of the equilibria

When $\tau =0$, we know that the basic reproduction number $R_0$, the rumor free equilibrium $E_0$, and the boundary equilibriums $E_1$, $E_2$, and positive equilibrium $E_3^{*}$ of system (2.1) will not change. In this section, when $\tau \ge 0$, we prove the globally asymptotic stability of the equilibrium $E_0$. when $\tau =0$, we prove the globally asymptotic stability of the equilibria $E_1$, $E_2$, and $E_3^{*}$.

Theorem 6

When $R_{11},R_{21}\le 1$, the rumor free equilibrium $E_0$ of system (2.3) is globally asymptotic stable when $\tau \ge 0$.

Proof

Let (S(t), E(t), I(t), M(t)) be any positive solution of system (2.3) with the initial condition (2.2). Define

$$\begin{aligned} V(t)=S-S^*-S^*\ln \frac{S}{S^*}+E+I+M+\int _{t-\tau }^{t}\delta \bar{k}S^*M(t)dt, \end{aligned}$$

where $S^*=\frac{A}{\mu }$. Calculating the derivative of V(t) along positive solutions of system(2.3), we have

$$\begin{aligned} \begin{aligned} \frac{dV}{dt}&= \left( 1-\frac{S^*}{S}\right) (A-\beta \bar{k} SI-\delta \bar{k} SM(t-\tau )+\mu (S^*-S))\\&\quad + (1-\alpha )\beta \bar{k} SI-\delta \bar{k} EM(t-\tau )- \gamma E-\varepsilon E-\mu E\\&\quad + \alpha \beta \bar{k} SI+\gamma E-\delta \bar{k} IM(t-\tau )-\varepsilon I-\mu I\\&\quad + \delta \theta \bar{k} M(t-\tau )(S+E+I)-\mu M\\&\quad +\delta \bar{k}S^*M-\delta \bar{k}S^*M(t-\tau ) \end{aligned} \end{aligned}$$

Noting that $S^*=\frac{A}{\mu }$, we have

$$\begin{aligned} \begin{aligned} \frac{dV}{dt}&= -\frac{\mu }{S}(S-S^*)^2+\beta \bar{k} S^*I+\delta \bar{k} S^*M(t-\tau )+\mu S^*\left( 2-\frac{S}{S^*}-\frac{S^*}{S}\right) \\&\quad -(1-\theta )\delta \bar{k}(S+E+I)M(t-\tau )-\varepsilon E-\mu E-\varepsilon I-\mu I-\mu M\\&\quad +\delta \bar{k}S^*M(t)-\delta \bar{k}S^*M(t-\tau )\\&\le \beta \bar{k} S^*I-(\varepsilon +\mu )I-(\varepsilon +\mu )E-(\mu -\delta \bar{k}S^*)M\\&=\left( \frac{\beta \bar{k}A}{\mu (\varepsilon +\mu )}-1\right) I-(\varepsilon +\mu )E-\left( 1-\frac{\delta \bar{k}A}{\mu ^2}\right) M\\&=(R_{11}-1)I-(\varepsilon +\mu )E-(1-R_{21})M \end{aligned} \end{aligned}$$

Define $R_{11}=\frac{\beta \bar{k}A}{\mu (\varepsilon +\mu )}$, and $R_{21}=\frac{\delta \bar{k}A}{\mu ^2}$. When $R_{11}\le 1$, and $R_{21}\le 1$ ensures $\frac{dV}{dt}\le 0$ for all $E(t), I(t), M(t)\ge 0$. The equation $\frac{dV}{dt}=0$ holds if and only if $E(t)=0, I(t)=0, M(t)=0$. According to the LaSelles Invariance Principle [38], when $R_{11},R_{21}\le 1$, the rumor free equilibrium of $E_0$ of system (2.3) is globally asymptotically stable. $\square$

Theorem 7

When $R_2>1$ and $\beta <\frac{\delta \theta (\delta \theta A \bar{k}+\mu \varepsilon )}{\mu ^2}$, the equilibrium $E_1$ of system (2.3) is globally asymptotic stable.

Proof

Let

$$\begin{aligned} V_1(t)= & {} S-S^*-S^*\ln \frac{S}{S^*},\\ V_2(t)= & {} M-M^*-M^*\ln \frac{M}{M^*},\\ V_3(t)= & {} E,V_4(t)=I. \end{aligned}$$

The derivatives of the above equations along the trajectory of system (2.3) are

$$\begin{aligned} \frac{dV_1}{dt}{} & {} = \left( 1-\frac{S^*}{S}\right) S{'}\\{} & {} =\left( 1-\frac{S^*}{S}\right) \left( -\beta \bar{k}SI+\delta \bar{k}S^*M^*\left( 1-\frac{SM}{S^*M^*}\right) +\mu (S^*-S)\right) \\{} & {} =-\beta \bar{k}SI+\beta \bar{k}S^*I+\delta \bar{k}S^*M^*\left( 1-\frac{S^*}{S}-\frac{SM}{S^*M^*}+ \frac{M}{M^*}\right) \\{} & {} \quad +\mu S^*\left( 2-\frac{S}{S^*}-\frac{S^*}{S}\right) ,\\ \frac{dV_2}{dt}{} & {} = \left( 1-\frac{M^*}{M}\right) M{'}\\{} & {} =\left( 1-\frac{M^*}{M}\right) \left( \delta \theta \bar{k}\left( MS-M^*S^*\frac{M}{M^*}\right) \right. \\{} & {} \quad \left. +\mu \left( M^*\frac{M}{M^*}-M\right) +\delta \theta \bar{k}M(E+I)\right) \\{} & {} = \delta \theta \bar{k}M^*S^*\left( \frac{MS}{M^*S^*}-\frac{S}{S^*}-\frac{M}{M^*}+1\right) +\left( 1-\frac{M^*}{M}\right) \delta \theta \bar{k}M(E+I),\\ \frac{dV_3}{dt}{} & {} = E{'}= (1-\alpha )\beta \bar{k}SI-\delta \bar{k}ME-\gamma E-\varepsilon E-\mu E,\\ \frac{dV_4}{dt}{} & {} = I{'}= \alpha \beta \bar{k}SI+\gamma E-\delta \bar{k}MI-\varepsilon I-\mu I. \end{aligned}$$

We construct the following Liapunov function:

$$\begin{aligned} \begin{aligned} V=V_1+\frac{1}{\theta }V_2+V_3+V_4, \end{aligned} \end{aligned}$$

Thus, we can obtain

$$\begin{aligned} \frac{dV}{dt}= & {} \frac{dV_1}{dt}+\frac{1}{\theta }\frac{dV_2}{dt}+\frac{dV_3}{dt}+\frac{dV_4}{dt}\\\le & {} \beta \bar{k}S^*I-\delta \bar{k}M^*(E+I)-\varepsilon (E+I)-\mu (E+I) \\= & {} \left( \frac{\beta \mu }{\delta \theta }-\mu R_2-\varepsilon \right) I-(\mu R_2+\varepsilon )E. \end{aligned}$$

When $\beta <\frac{\delta \theta (\delta \theta A \bar{k}+\mu \varepsilon )}{\mu ^2}$,then $\frac{\beta \mu }{\delta \theta }-\mu R_2-\varepsilon <0$, thus $\frac{dV}{dt}\le 0$. According to LaSalles Invariance Principle [38], $E_1$ of system (2.3) is globally asymptotically stable when $R_2>1$ and $\beta <\frac{\delta \theta (\delta \theta A \bar{k}+\mu \varepsilon )}{\mu ^2}$. $\square$

Theorem 8

When $R_1>1$, and $R_2<\frac{\beta A\bar{k}(\varepsilon +\mu +\gamma )R_1}{(\varepsilon +\mu +\gamma )\beta A\bar{k}+\mu ^2 R_1(R_1-1)+\mu \beta A\bar{k}(1-\alpha )(R_1-1)}$, the equilibrium $E_2$ of system (2.3) is globally asymptotic stable.

Proof

Let

$$\begin{aligned} V_1(t)= & {} S-S^*-S^*\ln \frac{S}{S^*},\\ V_2(t)= & {} M,\\ V_3(t)= & {} E-E^*-E^*\ln \frac{E}{E^*},\\ V_4(t)= & {} I-I^*-I^*\ln \frac{I}{I^*}. \end{aligned}$$

The derivatives of the above equations along the trajectory of system (2.3) are

$$\begin{aligned} \frac{dV_1}{dt}= & {} \left( 1-\frac{S^*}{S}\right) \left( -\beta \bar{k}SI+\beta \bar{k}S^*I^*-\delta \bar{k}SM+\mu (S^*-S)\right) \\= & {} \left( 1-\frac{S^*}{S}\right) \left( \beta \bar{k}S^*I^*\left( 1-\frac{SI}{S^*I^*}\right) -\delta \bar{k}SM+\mu (S^*-S)\right) \\= & {} \beta \bar{k}S^*I^*\left( 1-\frac{S^*}{S}+\frac{I}{I^*}-\frac{SI}{S^*I^*}\right) -\delta \bar{k}SM\left( 1-\frac{S^*}{S}\right) \\{} & {} +\mu S^*\left( 2-\frac{S^*}{S}-\frac{S}{S^*}\right) ,\\ \frac{dV_2}{dt}= & {} \delta \bar{k}\theta M (S+E+I)-\mu M,\\ \frac{dV_3}{dt}= & {} \left( 1-\frac{E^*}{E}\right) E^{'}\\= & {} \left( 1-\frac{E^*}{E}\right) \left( (1-\alpha )\beta \bar{k}\left( SI-S^*I^*\frac{E}{E^*}\right) -\delta \bar{k}EM\right) \\= & {} (1-\alpha )\beta \bar{k}S^*I^*\left( \frac{SI}{S^*I^*}-\frac{SEI}{S^*E^*I^*}-\frac{E}{E^*}+1\right) -\delta \bar{k}EM\left( 1-\frac{E^*}{E}\right) ,\\ \frac{dV_4}{dt}= & {} \left( 1-\frac{I^*}{I}\right) I^{'}\\= & {} \left( 1-\frac{I^*}{I}\right) \left( \alpha \beta \bar{k}\left( SI-S^*I^*\frac{I}{I^*}\right) +\left( \gamma E-\gamma E^*\frac{I}{I^*}\right) -\delta \bar{k}IM\right) \\= & {} \alpha \beta \bar{k}S^*I^*\left( \frac{SI}{S^*I^*}-\frac{I}{I^*}-\frac{S}{S^*}+1\right) +\gamma E^*\left( \frac{E}{E^*}-\frac{EI}{E^*I^*}-\frac{I}{I^*}+1\right) \\{} & {} -\delta \bar{k}IM\left( 1-\frac{I^*}{I}\right) . \end{aligned}$$

We set,

$$\begin{aligned} \begin{aligned} (1-\alpha )V_1^{'}+V_3^{'}&= (1-\alpha )\beta \bar{k}S^*I^*\left( 2-\frac{S^*}{S}+\frac{I}{I^*}-\frac{E}{E^*}-\frac{SIE^*}{S^*I^*E}\right) \\&\quad -(1-\alpha )\delta \bar{k}SM\left( 1-\frac{S^*}{S}\right) +(1-\alpha )\mu S^*\left( 2-\frac{S^*}{S}-\frac{S}{S^*}\right) \\&\quad - \delta \bar{k}EM\left( 1-\frac{E^*}{E}\right) ,\\ \alpha V_1^{'}+V_4^{'}&=\alpha \beta \bar{k}\left( 2-\frac{S^*}{S}-\frac{S}{S^*}\right) +\gamma E^*\left( \frac{E}{E^*}-\frac{EI}{E^*I^*}-\frac{I}{I^*}+1\right) \\&\quad -\delta \bar{k}IM\left( 1-\frac{I^*}{I}\right) -\delta \alpha \bar{k}SM\left( 1-\frac{S^*}{S}\right) \\&\quad +\alpha \mu S^*\left( 2-\frac{S^*}{S}-\frac{S}{S^*}\right) . \end{aligned} \end{aligned}$$

Then,

$$\begin{aligned} V^{*}{} & {} =\frac{1}{\alpha \beta \bar{k}S^*I^*+\gamma E^*}(V_1^{'}+V_3^{'}+V_4^{'}) \\{} & {} \le \left( 2-\frac{S^*}{S}+\frac{I}{I^*}-\frac{E}{E^*}-\frac{SIE^*}{S^*I^*E}\right) +\frac{(1-\alpha )\delta \bar{k}SM}{\alpha \beta \bar{k}S^*I^*+\gamma E^*}\left( \frac{S^*}{S}-1\right) \\{} & {} \quad +\left( \frac{E}{E^*}-\frac{EI}{E^*I^*}-\frac{I}{I^*}+1\right) +\frac{\delta \bar{k}IM}{\alpha \beta \bar{k}S^*I^*+\gamma E^*}\left( \frac{I^*}{I}-1\right) \\{} & {} \quad +\frac{\alpha \delta \bar{k}SM}{\alpha \beta \bar{k}S^*I^*+\gamma E^*}\left( \frac{S^*}{S}-1\right) +\frac{\delta \bar{k}EM}{\alpha \beta \bar{k}S^*I^*+\gamma E^*}\left( \frac{E^*}{E}-1\right) \\{} & {} \le \left( \ln \frac{S^*}{S}-\frac{S^*}{S}+\frac{I}{I^*}-\ln \frac{I}{I^*}+\frac{E}{E^*}-\ln \frac{E}{E^*}\right) \\{} & {} \quad + \frac{\delta \bar{k}SM}{\alpha \beta \bar{k}S^*I^*+\gamma E^*}\left( \frac{S^*}{S}-1\right) +\left( \frac{E}{E^*}-\ln \frac{E}{E^*}+\ln \frac{I}{I^*}-\frac{I}{I^*}\right) \\{} & {} \quad +\frac{\delta \bar{k}IM}{\alpha \beta \bar{k}S^*I^*+\gamma E^*}\left( \frac{I^*}{I}-1\right) +\frac{\delta \bar{k}EM}{\alpha \beta \bar{k}S^*I^*+\gamma E^*}\left( \frac{E^*}{E}-1\right) \\{} & {} \le \frac{\delta \bar{k}}{\alpha \beta \bar{k}S^*I^*+\gamma E^*}\left( SM\left( \frac{S^*}{S}-1\right) +IM\left( \frac{I^*}{I}-1\right) +EM\left( \frac{E^*}{E}-1\right) \right) . \end{aligned}$$

Thus, we construct the following Liapunov function:

$$\begin{aligned} \begin{aligned} V=\frac{A}{\mu ^2}V_2+\frac{1}{\alpha \beta \bar{k}S^*I^*+\gamma E^*}(V_1+V_2+V_4), \end{aligned} \end{aligned}$$

Thus, we can obtain

$$\begin{aligned} \frac{dV}{dt}= & {} \frac{A}{\mu ^2}\frac{dV_2}{dt}+\frac{1}{\alpha \beta \bar{k}S^*I^*+\gamma E^*}\left( \frac{dV_1}{dt}+\frac{dV_3}{dt}+\frac{dV_4}{dt}\right) \\= & {} \frac{A}{\mu ^2}(\delta \bar{k}\theta M (S+E+I)-\mu M)+V^*\\{} & {} \le \frac{\delta \bar{k}}{\alpha \beta \bar{k}S^*I^*+\gamma E^*}\left( SM(\frac{S^*}{S}-1)+IM\left( \frac{I^*}{I}-1\right) +EM\left( \frac{E^*}{E}-1\right) \right) \\{} & {} + M\left( R_2(S+E+I)-\frac{A}{\mu }\right) . \end{aligned}$$

When $R_2<\frac{\beta A\bar{k}(\varepsilon +\mu +\gamma )R_1}{(\varepsilon +\mu +\gamma )\beta A\bar{k}+\mu ^2 R_1(R_1-1)+\mu \beta A\bar{k}(1-\alpha )(R_1-1)}$, then $R_2(S+E+I)-\frac{A}{\mu }<0$, thus $\frac{dV}{dt}\le 0$. Furthermore, $\frac{dV}{dt}=0$ if and only if $S=S^*, E=E^*, I=I^*, M=M^*$. According to LaSalles Invariance Principle [38], $E_2$ of system (2.3) is globally asymptotically stable when $R_1>1$. $\square$

Next, we study the global asymptotic stability of positive equilibrium. When $R_0>1$, there is at least one positive equilibrium in system (2.3) and is uniformly persistent. Define $D_0=\{(S(t),E(t),I(t),M(t))\in D \mid$ At least one of E(t), I(t), and M(t) is greater than 0$\}$.

Theorem 9

When $R_0>1$, the positive equilibrium $E_3^{*}=(S^*,E^*,I^*,M^*)$ of system (2.3) is globally asymptotic stable in $D_0$.

Proof

Let

$$\begin{aligned} V_1(t)= & {} S-S^*-S^*\ln \frac{S}{S^*},\\ V_2(t)= & {} M-M^*-M^*\ln \frac{M}{M^*},\\ V_3(t)= & {} E-E^*-E^*\ln \frac{E}{E^*},\\ V_4(t)= & {} I-I^*-I^*\ln \frac{I}{I^*}. \end{aligned}$$

The derivatives of the above equations along the trajectory of system (2.3) are

$$\begin{aligned} \frac{dV_1}{dt}= & {} \left( 1-\frac{S^*}{S}\right) (A-\beta \bar{k}SI-\delta \bar{k}SM-\mu S)\\= & {} \left( 1-\frac{S^*}{S}\right) \left( \beta \bar{k}S^*I^*\left( 1-\frac{SI}{S^*I^*}\right) -\delta \bar{k}S^*M^*\left( 1-\frac{SM}{S^*M^*}\right) +\mu (S^*-S)\right) \\= & {} \beta \bar{k}S^*I^*\left( 1-\frac{S^*}{S}+\frac{I}{I^*}-\frac{SI}{S^*I^*}\right) -\delta \bar{k}S^*M^*\left( 1-\frac{S^*}{S}+\frac{M}{M^*}-\frac{SM}{S^*M^*}\right) \\{} & {} +\mu S^*\left( 2-\frac{S^*}{S}-\frac{S}{S^*}\right) ,\\ \frac{dV_2}{dt}= & {} \left( 1-\frac{M^*}{M}\right) \delta \bar{k}\theta M (S+E+I)-\mu M\\= & {} \left( 1-\frac{M^*}{M}\right) \bigg (\delta \theta \bar{k}\left( MS-M^*S^*\frac{M}{M^*}\right) \\{} & {} +\delta \theta \bar{k}\left( ME-M^*E^*\frac{M}{M^*}\right) +\delta \theta \bar{k}\left( MI-M^*I^*\frac{M}{M^*}\right) \bigg )\\= & {} \left( 1-\frac{M^*}{M}\right) \bigg (\delta \theta \bar{k}M^*S^*\left( \frac{MS}{M^*S^*}-\frac{M}{M^*}\right) +\delta \theta \bar{k}M^*E^*\left( \frac{ME}{M^*E^*}-\frac{M}{M^*}\right) \\{} & {} +\delta \theta \bar{k}M^*I^*\left( \frac{MI}{M^*I^*}-\frac{M}{M^*}\right) \bigg )=\delta \theta \bar{k}M^*S^*\left( \frac{MS}{M^*S^*}-\frac{S}{S^*}-\frac{M}{M^*}+1\right) \\{} & {} +\delta \theta \bar{k}M^*E^*\left( \frac{ME}{M^*E^*}-\frac{E}{E^*}-\frac{M}{M^*}+1\right) \\{} & {} +\delta \theta \bar{k}M^*I^*\left( \frac{MI}{M^*I^*}-\frac{I}{I^*}-\frac{M}{M^*}+1\right) ,\\ \frac{dV_3}{dt}= & {} \left( 1-\frac{E^*}{E}\right) ((1-\alpha )\beta \bar{k}SI-\delta \bar{k}EM-\gamma E-\varepsilon E- \mu E) \\= & {} \left( 1-\frac{E^*}{E}\right) \left( (1-\alpha )\beta \bar{k}\left( SI-S^*I^*\frac{E}{E^*}\right) -\delta \bar{k}\left( E^*M^*\frac{E}{E^*}-EM\right) \right) \\= & {} \left( 1-\frac{E^*}{E}\right) \left( (1-\alpha )\beta \bar{k}S^*I^*\left( \frac{SI}{S^*I^*}-\frac{SI}{S^*I^*}-\frac{E}{E^*}\right) \right. \\{} & {} \left. +\delta \bar{k}E^*M^*\left( \frac{E}{E^*}-\frac{EM}{E^*M^*}\right) \right) \\= & {} (1-\alpha )\beta \bar{k}S^*I^*\left( \frac{SI}{S^*I^*}-\frac{SEI}{S^*E^*I^*}-\frac{E}{E^*}+1\right) \\{} & {} -\delta \bar{k}E^*M^*\left( \frac{E}{E^*}-\frac{EM}{E^*M^*}+\frac{M}{M^*}-1\right) ,\\ \frac{dV_4}{dt}= & {} \left( 1-\frac{I^*}{I}\right) (\alpha \beta \bar{k} SI+\gamma E-\delta \bar{k} IM-\varepsilon I-\mu I)\\= & {} \left( 1-\frac{I^*}{I}\right) \left( \alpha \beta \bar{k}S^*I^*\left( \frac{SI}{S^*I^*}-\frac{I}{I^*}\right) +\gamma E^*\left( \frac{E}{E^*}-\frac{I}{I^*}\right) \right. \\{} & {} \left. -\delta \bar{k}I^*M^*\left( \frac{I}{I^*}-\frac{IM}{I^*M^*}\right) \right) \\= & {} \alpha \beta \bar{k}S^*I^*\left( \frac{SI}{S^*I^*}-\frac{I}{I^*}-\frac{S}{S^*}+1\right) \\{} & {} +\gamma E^*\left( \frac{E}{E^*}-\frac{EI}{E^*I^*}-\frac{I}{I^*}+1\right) \\{} & {} -\delta \bar{k}I^*M^*\left( \frac{I^*}{I}-1-\frac{IM}{I^*M^*}+\frac{M}{M^*}\right) . \end{aligned}$$

We construct the following Liapunov function:

$$\begin{aligned} \begin{aligned} V=\frac{1}{(1-\alpha )\beta \bar{k}S^*I^*+\gamma E^*}\left( V_1+\frac{1}{\theta }V_2+V_3+V_4\right) , \end{aligned} \end{aligned}$$

Where

$$\begin{aligned} V_1+\frac{1}{\theta }V_2+V_3+V_4\le & {} (1-\alpha )\beta \bar{k}S^*I^*\\{} & {} \left( \ln \frac{S^*}{S}-\frac{S^*}{S}+\frac{I}{I^*}-\ln \frac{I}{I^*}+\ln \frac{E}{E^*}-\frac{E}{E^*}\right) \\{} & {} \quad +\gamma E^*\left( \frac{E}{E^*}-\ln \frac{E}{E^*}+\ln \frac{I}{I^*}-\frac{I}{I^*}\right) \end{aligned}$$

Then we can obtain

$$\begin{aligned} \begin{aligned} \frac{dV}{dt}= \frac{1}{(1-\alpha )\beta \bar{k}S^*I^*+\gamma E^*}\left( \ln \frac{S^*}{S}-\frac{S^*}{S}\right) \le 0. \end{aligned} \end{aligned}$$

Furthermore, $\frac{dV}{dt}=0$ if and only if $S=S^*, E=E^*, I=I^*, M=M^*$. According to LaSalles Invariance Principle [38], $E_3^{*}$ of system (2.3) is globally asymptotically stable in the region $D_0$ when $R_0>1$. $\square$

4 Numerical simulation

In this section, the theoretical results and the influence of the key parameters of model are verified by numerical simulations, and the influence of time delay on rumor propagation for system (2.3) is analyzed. Finally, the results showed that the SEIMR model is more realistic and conforms to the rules of rumor spreading by comparative experiments.

4.1 Stability simulation and analysis for system (2.3)

Considering system (2.3) with the parameters in Data 1 of Table 1, $R_0 \approx 0.67<1$ can be obtained, and they satisfy the stability condition of $E_0$. Based on Theorem 3, the equilibrium $E_0$ is locally asymptotically stable. The time series graph in Fig. 2a depicts the density of S(t), E(t), I(t),  and M(t) as a function of time from system (2.3). From Fig. 2b, in the case of different initial values, the trajectories change the process of the density of S(t), I(t),  and M(t). The five initial values selected from Data 1 of Table 2. As can be seen from Fig. 2, when $R_0<1$, the density of expose, infective, media, and remover finally changes to 0, and there is no rumor spreader in the system. And the change of the initial value does not affect the system.

Table 1 Parameters for the local stability of $E_0, E_1, E_2$, and $E_{3}^*$

Table 2 Different initial conditions of S(0), E(0), I(0), and M(0).

Fig. 2

Equilibrium $E_0$: a time series graph of S(t), E(t), I(t), and M(t), b Phase plan of five different initial values

Fig. 3

Equilibrium $E_1$: a Time series graph of S(t), E(t), I(t), and M(t), b Phase plan of five different initial values

Considering system (2.3) with parameters in Data 2 of Table 1, then $R_2=2.24>1$ and $\beta =0.6<\frac{\delta \theta (\delta \theta A \bar{k}+\mu \varepsilon )(\delta \theta A \bar{k}+\mu \varepsilon +\mu \gamma )}{\mu ^2(\delta \theta A \bar{k}\alpha +\alpha \varepsilon \mu +\gamma \mu )}\approx 4.45$ and they satisfy the stability condition of $E_1$. Based on Theorem 4, the equilibrium $E_1$ is locally asymptotically stable. As shown in Fig. 3a, system (2.3) finally reaches a stable state. From Fig. 3b, in the case of different initial values, the trajectories change the density of S(t), I(t),  and M(t). The five initial values are selected from Data 2 of Table 2. As shown in Fig. 3, when the condition of Theorem 4 is established, the density of infective first increases and decreases to 0, and the density of media reports gradually increases and finally reaches a steady state. Finally, only media reports and susceptible exist in the system.

Fig. 4

Equilibrium $E_2$: a Time series graph of S(t), E(t), I(t), and M(t), b Phase plan of five different initial values

Considering system (2.3) with parameters in Data 3 of Table 1, then $R_1\approx 1.1>1$, $R_2\approx 0.1<\frac{\beta A\bar{k}(\varepsilon +\mu +\gamma )R_1}{(\varepsilon +\mu +\gamma )\beta A\bar{k}+\mu ^2 R_1(R_1-1)+\mu \beta A\bar{k}(1-\alpha )(R_1-1)}\approx 1.1$ and they satisfy the stability condition of $E_2$. Based on Theorem 5, the equilibrium $E_2$ is locally asymptotically stable. As shown in Fig. 4a, system (2.3) finally reaches a stable state. From Fig. 4b, in the case of different initial values, the trajectories change the density of S(t), I(t),  and M(t). The five initial values are selected from Data 3 of Table 2. As shown in Fig. 4, when the condition of Theorem 5 is established, the density of infective and exposed gradually increases and finally reaches a steady state, and the density of media report gradually decreases to 0. Finally, only susceptible, exposed and infective exist in the system. And the change of the initial value does not affect the final state of the system.

Finally, in Fig. 5, the existence of positive equilibrium of system (2.3) is verified with the parameters in Data 4 of Table 1, then $\frac{\alpha \beta \mu }{\delta \theta \varepsilon }\approx 0.002>0$, and they satisfy the existence condition of $E_{3}^*$. From Fig. 5a, in the case of different initial values, the trajectories change the density of S(t), I(t),  and M(t). The five initial values are selected from Data 4 of Table 2. As shown in Fig. 5, when the existence condition of $E_{31}^*$ is satisfy, the density of susceptible, infective, exposed, and media reports gradually increases and finally reaches a steady state, which verifies the existence of equilibrium $E_{3}^*$ in the system.

Fig. 5

Equilibrium $E_{3}^*$: a Time series graph of S(t), E(t), I(t), and M(t), b Phase plan of five different initial values

4.2 Influence of important parameters for system (2.3)

In this section, we will analyze the influence of different contact rates $\beta$, rumor spread infection rate $\alpha$, media report influence $\delta$, $\theta$, network average $\bar{k}$ and initial value of media report M(0) on rumor spread.

Table 3 Parameters of important influencing for rumor propagation

Fig. 6

The densities evolution of I(t) with different $\beta$ and $\alpha$

Fig. 7

The densities evolution of I(t) with different $\delta$ and $\theta$

From Fig. 6, the peak of I(t) becomes larger as the rates $\beta$, and $\alpha$ increase. As the infection rate and blind forwarding rate increase, rumor spreaders will become more numerous, and the longer the rumor spreads, the higher the peak of rumor spreaders will be, and eventually become stable.

From Fig. 7, the peak of I(t) becomes smaller as the rate $\delta$, and $\theta$ increase. As the rate of media coverage and crowd forwarding increases, more people become aware of the true information. The increased willingness of people to forward information about the refuted rumor information from media reports. Thus, fewer people spread rumors, resulting in a lower peak of rumor spreaders and a reduction in the duration of rumor spreading.

Fig. 8

a The densities evolution of I(t) with different $\bar{k}$, b The densities evolution of I(t) with different initial values of M(0)

Table 4 Parameters for SEIMR and SEIR models

Figure 8a reflects the density evolution of rumor spread for different values of $\bar{k}$. The simulation results show that with the increase of $\bar{k}$ value, the rumor spreaders will reach a higher peak in a shorter period of time. And the network average degree $\bar{k}$ indicates the closeness of the relationship between network users, so if the contact between users in the social network is closer, it will further promote the spread of rumors.

Figure 8b reflects the density evolution of rumor spread for different values of M(0). A higher initial value of media reports means that there will be more information to dispel rumors, the peak of rumor spreaders will be reduced, and the rumor propagation time will be shortened. It can be seen that more initial values of media reports will be more beneficial to control the scale of rumor propagation.

4.3 Influence of time delay for system (2.3)

In this section, the influence of time delay on rumor propagation is discussed. Selecting Data 1 of Table 1, then $R_1 \approx 0.9<1$; thus, system (2.3) has equilibrium $E_0$. As shown in Fig. 9a, the longer the reaction time of media reports, the greater the peak of rumor spreading. On the other hand, selecting Data 2 of Table 1, then $R_2=2.24>1$ and $\beta =0.6<\frac{\delta \theta (\delta \theta A \bar{k}+\mu \varepsilon )(\delta \theta A \bar{k}+\mu \varepsilon +\mu \gamma )}{\mu ^2(\delta \theta A \bar{k}\alpha +\alpha \varepsilon \mu +\gamma \mu )}\approx 4.45$, thus system (2.3) has equilibrium $E_1$. As shown in Fig. 9b, we can find that not only does the peak of rumor propagation increase with the increase of time delay, but the rumor duration also becomes longer. From a rumor control perspective, the sooner rumors are accurately refuted and authoritative reports are released, the better the results will be, so that the harm caused to society by rumors can be reduced.

Fig. 9

Influence of time delay $\tau$ for system (2.3)

4.4 Compare of SEIMR and SEIR models

In this section, the effectiveness of the SEIMR model has been verified via the comparative experiments. Except for the media influence rate $\delta$ and the rate $\theta$, the other parameters of the SEIMR model are the same and all parameters of the SEIR model. Table 4 lists the specific parameter values.

Fig. 10

Comparison of the SEIMR model and the SEIR model

From Fig. 10, by selecting different parameter values, two groups of experimental results can be obtained. Data 1 and Data 2 of Table 4 correspond to Fig. 10a and b. From Fig. 10a, the density of rumor spreaders in ours model increases first and then decreases to 0, while in the traditional SEIR model, the density of rumor spreaders increases first and then tends to steady state. From Fig. 10b, the density of rumor spreaders in ours model increases first and then decreases and gradually tends to a steady state. However, the density of rumor spreaders in the traditional SEIR model gradually increases and tends to steady state. To sum up, the model in this paper is more consistent with the spreading rules of rumors after the addition of media reports, and it can be obtained by comparing with the experimental results of the traditional model. The model in this paper can provide theoretical support for the rumor prevention and control of government departments.

5 Conclusion

In this paper, a SEIMR rumor propagation model on social networks is proposed. The influence of media reports and time delay on rumor spreading is studied. Firstly, the basic reproduction number $R_0$ of the model is obtained. Secondly, the positivity, boundness, and existence of the solutions of the model are analyzed. Then, the local asymptotic stability of the rumor free equilibrium $E_0$ and the boundary equilibriums $E_1$ and $E_2$ is proved, and the global asymptotic stability of the equilibriums $E_0$, $E_1$, $E_2$, $E_3^{*}$ is proved by constructing the Lyapunov function. Finally, the accuracy of the theoretical results as well as the effects of different parameters of the model have been verified through numerical simulations, and the effectiveness of the SEIMR model has been verified via comparative experiments. The research shows that in the process of rumor spreading, the influence of media reports is very consistent with reality. In addition, by increasing the initial number of rumor-refuting media and increasing the reaction speed of the authoritative media to refute rumors, i.e., decreasing the time delay $\tau$, the harm brought by rumor spreading to society can be reduced.

Through the mathematical test of the rumor spreading model, it is found that rumor spreading is a very complicated process. Mathematical analysis can provide a theoretical basis for controlling the spread of rumors and reducing their harmful effects. This paper does not consider the influence of network structure on rumor spread and the more complex behavior of rumor refuting. In the future, we will study the dynamic law of rumor propagation evolution under the joint effect of external rumor refutation information reported by the media and individual rumor refutation behavior, and the evolution law of rumors under different network structures.