1 Introduction

Over the last several decades, infectious disease models have gained increasing recognition as a powerful tool to reveal the mechanism spread of diseases. Based on systems design with deterministic and stochastic models, there are a lot of literatures to investigate the transmission rates of diseases, see [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27] and the references therein. One of classic epidemic models is the SEIR model, which subdivides a homogeneous host population into categories containing susceptible, exposed, infectious and recovered individuals, with their population sizes denoted by S, E, I and R, respectively. Anderson and May [2] first used a system of ordinary differential equations (ODEs) to describe a classical SEIR epidemic model in 1991. Later, ODEs, IDEs, PDEs and SDEs are heavily employed to investigate SEIR epidemic models and many good results are obtained, for details to see [3, 22,23,24,25,26,27,28,29,30]. In particular, Zhao et al. [30] established and studied an SEIR model with non-communicability in incubation period. But, for some diseases, such as COVID-19, the incubation period is infectious [31], and the COVID-19 outbreak control in China shows that both physical protection [32,33,34] and social isolation [35,36,37] play important roles in controlling the epidemic in the present absence of vaccines for the virus. With the idea of infectivity in incubation period, Jiao et al. [38] proposed a deterministic SEIR epidemic model with homestead–isolation on the susceptible

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle {\dot{S}}(t)=\Lambda -\beta (1-\theta _1)S(t)[I(t)+\theta _{2}E(t)]-\mu S(t),\\ {\dot{E}}(t)=\beta (1-\theta _1)S(t)[I(t)+\theta _{2}E(t)]-(\delta +\mu )E(t),\\ {\dot{I}}(t)=\delta E(t)-(\gamma +\alpha +\mu )I(t),\\ {\dot{R}}(t)=(\gamma +\theta _{3}\alpha )I(t)-\mu R(t), \end{array} \right. \end{aligned}$$
(1.1)

where \(\delta >\theta _2(\gamma +\alpha +\mu )\), and the biological meanings of the parameters of model (1.1) are shown in Table 1 below.

Table 1 The biological significance of each parameter for model (1.1)
Full size table

Since the variable R in the fourth equation is not involved in the first three equations of model (1.1), a reasonable idea is to consider the following model

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle {\dot{S}}(t)=\Lambda -\beta (1-\theta _1)S(t)[I(t)+\theta _{2}E(t)]-\mu S(t),\\ {\dot{E}}(t)=\beta (1-\theta _1)S(t)[I(t)+\theta _{2}E(t)]-(\delta +\mu )E(t),\\ {\dot{I}}(t)=\delta E(t)-(\gamma +\alpha +\mu )I(t). \end{array} \right. \end{aligned}$$
(1.2)

It follows from [38] that the basic reproduction number is \(R_0=\frac{\Lambda \beta (1-\theta _1)[\delta +\theta _2(\gamma +\alpha +\mu )]}{\mu (\gamma +\delta +\mu )(\delta +\mu )}\), and the threshold dynamics results of model (1.2) are summarized as follows:

\(\bullet \) The positive equilibrium (denoted by \(P^*\)) is globally asymptotically stable if \(R_0>1\);

\(\bullet \) The disease-free equilibrium (denoted by \(P^0\)) is globally asymptotically stable provided that \(R_0<1\).

Admittedly, deterministic model has significant advantages in simplifying the complex system and facilitating the theoretical analysis, whereas there exist some limitations in describing the population dynamics by this modeling method, especially when the external interference is relatively large and the population number decreases dramatically due to large-scale natural disasters including hurricanes, tsunamis, volcanoes, earthquakes such that the law of large numbers becomes no longer available and the dynamical behaviors have changed even more radically compared with the corresponding deterministic models [39,40,41]. For example, Arnold et al. [39] found that the real environmental white noise could make the stable Lotka-Volterra system no longer stable, even a stationary solution no longer exists. Zhou et al. [40] revealed that random effects may lead the disease to extinction in scenarios where the deterministic model exhibits persistence. Since the fluctuations in the randomly varying environment, such as humidity, temperature, food supply, season, etc., constantly affect the biological population densities [42], which embodies the objectivity and universality of the stochasticity. Accordingly, some researchers have argued that stochastic differential equations (SDEs) should be used to model epidemic systems because they are inevitably affected by the environmental noises, thus their stochastic dynamics have been intensively studied, for example, persistence and extinction [12, 16,17,18,19,20, 23], asymptotic stability [24, 25], positive recurrent [20, 23], stationary distribution [6, 16,17,18,19, 43, 44], periodic solution [43, 44], optimal vaccination strategy [14] and so on.

In the last few years, numerous good works [23, 45,46,47,48] on stochastic SEIR epidemic model have sprung up that focused on the effects of stochastic perturbation on their transmission dynamics. In particular, Yang and Mao [23] observed that the dynamical behaviors of the perturbed SEIR models be considerably different from that of the deterministic counterpart, namely, large perturbations can accelerate the extinction of epidemics regardless of the magnitude of the basic reproduction number \(R_0\). Applying Lyapunov method Zhang and Wang [45] achieved the conditions for the stochastic stability, persistence and extinction of an SEIR model driven simultaneously by white and Lévy noises (termed jumps) which can capture the wide spread of infectious diseases caused by medical negligence. More recently, Boukanjime et al. [46] utilized a stochastic SEIR model to describe the COVID-19 transmission dynamics affected by mixture of white and telegraph noises and investigated the extinction and persistence in the mean of the COVID-19 epidemic in Indian states in terms of the stochastic threshold \(R_0\).

It should also be mentioned that several possible approaches incorporating stochastic effects into the epidemic models have been proposed and extensively studied. Thereinto, one well-known approach to construct the discrete-time or continuous-time Markov chain models [49,50,51], which are conducive to estimating parameters and exploring the implications of the models by using statistical methods and simulation (e.g., seeing [50, 51]). Artalejo and his coauthors [50] formulated a stochastic SEIR model described by a continuous-time Markov chain and developed efficient computational procedures for the distribution of the duration of an outbreak. Another frequently used approach is to incorporate the noises (such as the white, color, Lévy, telegraph noises or the coupling noises between them) into certain deterministic epidemic models [20, 43,44,45,46]. This approach is mainly involved in the following several different forms of perturbations: the noises may perturb model parameters [23, 52,53,54,55,56], or be proportional to the distance between the state variables and the endemic equilibria of the deterministic models [24, 57, 58], or proportional to the state variables measuring population densities [19, 25, 43, 47, 59], with the advantage of good understanding the stochastic dynamics in long time of these models from the theoretical analysis perspective. For instance, Liu et al. [25] analyzed asymptotic behaviors of the equilibria of a stochastic delayed nonlinear SEIR epidemic model via Lyapunov functions.

This contribution is interested in probing into stochastic dynamics of model (1.2) incorporating random perturbations by thorough mathematical analysis. Therefore, following [25, 47, 59], we suppose that random perturbations are proportional to the variables S, E and I in model (1.2) under the influence of white noises and get a stochastic model

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle dS(t)=[\Lambda -\beta (1-\theta _1)S(t)(I(t)+\theta _{2}E(t))-\mu S(t)]dt+\sigma _{1}S(t)dB_{1}(t),\\ dE(t)=[\beta (1-\theta _1)S(t)(I(t)+\theta _{2}E(t))-(\delta +\mu )E(t)]dt+\sigma _{2}E(t)dB_{2}(t), \\ dI(t)=[\delta E(t)-(\gamma +\alpha +\mu )I(t)]dt+\sigma _{3}I(t)dB_{3}(t), \end{array} \right. \qquad \end{aligned}$$
(1.3)

where \({\dot{B}}_i(t)\) are the white noises which are regarded as the derivative of mutually independent standard Brownian motions \(B_i(t)\ (i=1,2,3)\). \(\sigma _i^2>0\ (i=1,2,3)\) are the intensities of the noises and \(B_i(t)\) are defined on the complete probability space \((\Omega ,{\mathcal {F}},\{{\mathcal {F}}_t\}_{t\ge 0},{\mathbb {P}})\). Also, we assign \({\mathbb {R}}_+^n=\{x\in {\mathbb {R}}^n: x_j>0,1\le j\le n\}\).

Our main purpose of this work is to investigate the effects of environmental noises on the stochastic dynamics of model (1.3) and reveal whether the noises can inhibit the disease or not by comparing with the global dynamical results of model (1.2) established in [38]. The rest organization is as follows. Section 2 focuses on the extinction and strong persistence in the mean of the disease. Section 3 discusses the existence of a unique ergodic stationary distribution. Numerical simulations are conducted to substantiate our analytical results in Sect. 4. A brief biological discussion is provided in the final section.

2 Survival results of the disease

The section focuses on the survival results of the disease, and we first give the following two lemmas (Lemmas 2.1 and 2.2).

Lemma 2.1

For initial value \((S(0),E(0),I(0))\in {\mathbb {R}}_+^3\), there is a unique solution (S(t), E(t), I(t)) of model (1.3) on \(t\ge 0\) and the solution remains in \({\mathbb {R}}_+^3\) with probability one.

Assign \(W(S,E,I)=(S-a-a\ln \frac{S}{a})+(E-1-\ln E)+\frac{a\beta (1-\theta _1)}{\mu +\alpha +\gamma }(I-1-\ln I)\), where \(a=(\delta +\mu )/[\beta (1-\theta _1)(\theta _2+\frac{\delta }{(\mu +\gamma +\alpha )})]\), the rest proof is similar to Theorem 2.1 in [25], and we omit it here.

The following Lemma 2.2 is useful for the proofs of Theorems 2.1–2.2.

Lemma 2.2

Let (S(t), E(t), I(t)) be the solution of (1.3), then \(\lim \sup _{t\rightarrow +\infty }(S(t)+E(t)+I(t))<+\infty \), \(\lim _{t\rightarrow +\infty }S(t)/t=0\), \(\lim _{t\rightarrow +\infty }E(t)/t=0\), \(\lim _{t\rightarrow +\infty }I(t)/t=0\), \(\lim _{t\rightarrow +\infty }\ln S(t)/t=0\), \(\lim _{t\rightarrow +\infty }\ln E(t)/t=0\), \(\lim _{t\rightarrow +\infty }\ln I(t)/t=0\), a.s. And \(\lim _{t\rightarrow +\infty }\int _0^t S(r)dB_1(r)/t=0\), \(\lim _{t\rightarrow +\infty }\int _0^t E(r)dB_2(r)/t=0\), \(\lim _{t\rightarrow +\infty }\int _0^t I(r)dB_3(r)/t=0\), a.s.

Proof

It follows from (1.3) that

$$\begin{aligned} d(S+E+I)= & {} [\Lambda -\mu (S+E+I)-(\alpha +\gamma )I]dt\nonumber \\&+\sigma _1SdB_1+\sigma _2EdB_2+\sigma _3IdB_3, \end{aligned}$$
(2.1)

and we obtain, by solving the above equation (2.1), that

$$\begin{aligned}&S(t)+E(t)+I(t)\nonumber \\&\quad =\frac{\Lambda }{\mu }+\left( S(0)+E(0)+I(0)-\frac{\Lambda }{\mu }\right) e^{-\mu t} -(\alpha +\gamma )\int _0^t I(r)e^{-\mu (t-r)}dr\nonumber \\&\qquad +\sigma _1\int _0^t S(r)e^{-\mu (t-r)}dB_1(r)+\sigma _2\int _0^t E(r)e^{-\mu (t-r)}dB_2(r)\nonumber \\&\qquad +\sigma _3\int _0^t I(r)e^{-\mu (t-r)}dB_3(r)\nonumber \\&\quad \le \frac{\Lambda }{\mu }+\left( S(0)+E(0)+I(0)-\frac{\Lambda }{\mu }\right) e^{-\mu t}+\sigma _1\int _0^t S(r)e^{-\mu (t-r)}dB_1(r)\nonumber \\&\qquad +\sigma _2\int _0^t E(r)e^{-\mu (t-r)}dB_2(r)+\sigma _3\int _0^t I(r)e^{-\mu (t-r)}dB_3(r). \end{aligned}$$
(2.2)

Let

$$\begin{aligned} M(t)= & {} \sigma _1\int _0^t S(r)e^{-\mu (t-r)}dB_1(r)+\sigma _2\int _0^t E(r)e^{-\mu (t-r)}dB_2(r)\\&+\sigma _3\int _0^t I(r)e^{-\mu (t-r)}dB_3(r). \end{aligned}$$

Clearly, M(t) is a continuous local martingale with \(M(0)=0\).

Define

$$\begin{aligned} X(t)=X(0)+H(t)-Y(t)+M(t), \end{aligned}$$

where

$$\begin{aligned} X(0)= & {} S(0)+E(0)+I(0), H(t)=\frac{\Lambda }{\mu }(1-e^{-\mu t}),\\ Y(t)= & {} (S(0)+E(0)+I(0))(1-e^{-\mu t}). \end{aligned}$$

It follows from (2.2) that \(S(t)+E(t)+I(t)\le X(t)\) for all \(t>0\). Obviously, H(t) and Y(t) are continuous adapted increasing processes on \(t\ge 0\) with \(H(0)=Y(0)=0\). Applying Theorem 3.9 in [60], we obtain \(\lim _{t\rightarrow +\infty }X(t)<+\infty \). Hence

$$\begin{aligned} \limsup _{t\rightarrow +\infty }(S(t)+E(t)+I(t))<+\infty . \end{aligned}$$
(2.3)

Thus, one easily derives

$$\begin{aligned}&\displaystyle \lim _{t\rightarrow +\infty }\frac{S(t)}{t}=0,\lim _{t\rightarrow +\infty }\frac{E(t)}{t}=0, \lim _{t\rightarrow +\infty }\frac{I(t)}{t}=0,\\&\displaystyle \lim _{t\rightarrow +\infty }\frac{\ln S(t)}{t}=0,\lim _{t\rightarrow +\infty }\frac{\ln E(t)}{t}=0,\lim _{t\rightarrow +\infty }\frac{\ln I(t)}{t}=0. \end{aligned}$$

Assign

$$\begin{aligned} M_{1}(t)=\int _0^t S(r)dB_{1}(r),\ \ M_{2}(t)=\int _0^t E(r)dB_{2}(r),\ \ M_{3}(t)=\int _0^t I(r)dB_{3}(r). \end{aligned}$$

It follows from the quadratic variations that

$$\begin{aligned} \langle M_{1}(t),M_{1}(t)\rangle =\int _0^t S^{2}(r)dr\le \left( \sup _{t\ge 0}S^{2}(t)\right) t. \end{aligned}$$

By the large number theorem for martingale (see [60]) and (2.3), one has

$$\begin{aligned} \lim _{t\rightarrow +\infty }\frac{\int _0^t S(r)dB_1(r)}{t}=0. \end{aligned}$$

Similarly, we have

$$\begin{aligned} \lim _{t\rightarrow +\infty }\frac{\int _0^t E(r)dB_2(r)}{t}=0,\ \ \lim _{t\rightarrow +\infty }\frac{\int _0^t I(r)dB_3(r)}{t}=0. \end{aligned}$$

The proof of the desired conclusions is finished. \(\square \)

Next, we consider the extinction of the disease.

Theorem 2.1

If \({\hat{R}}_{0}=\frac{2\Lambda \beta (1+\theta _2)(1-\theta _1)(\delta +\mu )^2}{\mu [(\delta +\mu )^{2} (\gamma +\alpha +\mu +\frac{1}{2}\sigma _3^2)\wedge \frac{1}{2}\delta ^{2}\sigma _2^2]}<1\), then the disease I(t) will be extinct.

Proof

Integrating both sides of (2.1) over the interval [0, t] and dividing by t lead to

$$\begin{aligned}&\frac{1}{t}\int ^t_0d(S(s)+E(s)+I(s))\\&\quad \le \Lambda -\frac{\mu }{t}\int ^t_0(S(s)+E(s)+I(s))ds+\sigma _1\frac{1}{t}\int ^t_0S(s)dB_1(s)\\&\qquad +\sigma _2\frac{1}{t}\int ^t_0E(s)dB_2(s)+\sigma _3\frac{1}{t}\int ^t_0I(s)dB_3(s), \end{aligned}$$

from which we conclude that

$$\begin{aligned}&\frac{S(t)+E(t)+I(t)}{t}-\frac{S(0)+E(0)+I(0)}{t}\\&\quad \le \Lambda -\frac{\mu }{t}\int ^t_0(S(s)+E(s)+I(s))ds +\sigma _1\frac{1}{t}\int ^t_0S(s)dB_1(s)\\&\qquad +\sigma _2\frac{1}{t}\int ^t_0E(s)dB_2(s) +\sigma _3\frac{1}{t}\int ^t_0I(s)dB_3(s). \end{aligned}$$

We can know from Lemma 2.2 that

$$\begin{aligned} \limsup \limits _{t\rightarrow +\infty }\frac{1}{t}\int ^t_0(S(s)+E(s)+I(s))ds\le \Lambda /\mu . \end{aligned}$$
(2.4)

Let \(A(t)=\delta E(t)+(\delta +\mu )I(t)\). Applying Itô’s formula yields

$$\begin{aligned}&d\ln A(t)\nonumber \\&\quad =\left[ \frac{\beta (1-\theta _1)\delta SI}{\delta E+(\delta +\mu )I}+\frac{\beta (1-\theta _1)\delta \theta _2SE}{\delta E+(\delta +\mu )I}-\frac{(\delta +\mu )(\gamma +\alpha +\mu )I}{\delta E+(\delta +\mu )I}\right. \nonumber \\&\qquad \left. -\frac{\delta ^{2}\sigma _{2}^{2}E^{2}+(\delta +\mu )^{2}\sigma _{3}^{2}I^{2}}{2(\delta E +(\delta +\mu )I)^2}\right] dt\nonumber \\&\qquad +\frac{\delta \sigma _2 E}{\delta E+(\delta +\mu )I}dB_{2}(t) +\frac{(\delta +\mu )\sigma _3 I}{\delta E+(\delta +\mu )I}dB_{3}(t)\nonumber \\&\quad \le \beta (1-\theta _1)(1+\theta _2)Sdt-\frac{1}{(\delta E+(\delta +\mu )I)^2}\nonumber \\&\quad \qquad \left\{ \left[ (\delta +\mu )^{2}(\gamma +\alpha +\mu )+\frac{1}{2}(\delta +\mu )^{2}\sigma _3^2\right] I^{2}\right. \nonumber \\&\qquad \left. +\frac{1}{2}\delta ^{2}\sigma _2^2E^2\right\} dt+\frac{\delta \sigma _2 E}{\delta E+(\delta +\mu )I}dB_{2}(t) +\frac{(\delta +\mu )\sigma _3 I}{\delta E+(\delta +\mu )I}dB_{3}(t)\nonumber \\&\quad \le \beta (1-\theta _1)(1+\theta _2)Sdt-\frac{1}{2(\delta +\mu )^2}\nonumber \\&\quad \qquad \left[ (\delta +\mu )^{2} \left( \gamma +\alpha +\mu +\frac{1}{2}\sigma _3^2\right) \wedge \frac{1}{2}\delta ^{2}\sigma _2^2\right] dt\nonumber \\&\qquad \displaystyle +\frac{\delta \sigma _2 E}{\delta E+(\delta +\mu )I}dB_{2}(t)+\frac{(\delta +\mu )\sigma _3 I}{\delta E+(\delta +\mu )I}dB_{3}(t). \end{aligned}$$
(2.5)

Integrating both sides of (2.5) over the interval [0, t], dividing by t, and combining with (2.4) and Lemma 2.2, we have

$$\begin{aligned}&\liminf \limits _{t\rightarrow +\infty }\sup \frac{\ln A(t)}{t} \le \frac{\Lambda \beta (1-\theta _1)(1+\theta _2)}{\mu }\\&\qquad -\frac{1}{2(\delta +\mu )^2} \left[ (\delta +\mu )^{2}\left( \gamma +\alpha +\mu +\frac{1}{2}\sigma _3^2\right) \wedge \frac{1}{2}\delta ^{2}\sigma _2^2\right] \\&\quad =\frac{1}{2(\delta +\mu )^2}\left[ (\delta +\mu )^{2}\left( \gamma +\alpha +\mu +\frac{1}{2}\sigma _3^2\right) \wedge \frac{1}{2}\delta ^{2}\sigma _2^2\right] ({\hat{R}}_0-1)<0, \end{aligned}$$

which implies that

$$\begin{aligned} \lim _{t\rightarrow +\infty }I(t)=0,\ \ \lim _{t\rightarrow +\infty }E(t)=0. \end{aligned}$$

Thus, the disease I(t) will be extinct. \(\square \)

Assumption A

\(R_0^s =\frac{\beta (1-\theta _1)\Lambda \delta }{\left( \frac{1}{2}\sigma _1^{2}+\mu \right) \left( \frac{1}{2}\sigma _3^{2}+\mu +\gamma +\alpha \right) \left( \frac{1}{2}\sigma _2^{2} +\mu +\delta \right) }>1\).

Finally, we give the persistence of the disease.

Theorem 2.2

If Assumption A holds, then the disease I(t) will be strong persistent in the mean, and

$$\begin{aligned} \liminf \limits _{t\rightarrow +\infty }\frac{1}{t}\int _0^t I(s)ds\ge \frac{(\delta +\mu +\frac{1}{2}\sigma _2^2)(R_0^s-1)}{c_1\beta (1-\theta _1) +c_2\beta (1-\theta _1)\theta _2\frac{\gamma +\alpha +\mu }{\delta }}>0. \end{aligned}$$

Proof

Integrating on both sides of the last equation of (1.3) over the interval [0, t] and dividing by t lead to

$$\begin{aligned} \frac{I(t)-I(0)}{t}=\frac{\delta }{t}\int ^t_0E(s)ds -\frac{\gamma +\alpha +\mu }{t}\int ^t_0I(s)ds+\frac{\sigma _3}{t}\int _0^t I(s)dB_{3}(s). \end{aligned}$$

We computer that

$$\begin{aligned} \frac{1}{t}\int ^t_0E(s)ds=\frac{\gamma +\alpha +\mu }{\delta t}\int ^t_0I(s)ds+\psi (t), \end{aligned}$$
(2.6)

where

$$\begin{aligned} \psi (t)=\frac{1}{\delta }\Bigl [\frac{I(t)-I(0)}{t}-\frac{\sigma _3}{t}\int _0^t I(s)dB_{3}(s)\Bigr ]. \end{aligned}$$

It follows from Lemma 2.2 that we have

$$\begin{aligned} \lim _{t\rightarrow +\infty }\psi (t)=0. \end{aligned}$$
(2.7)

Assign

$$\begin{aligned} U(S,E,I)=-c_1\ln S-c_2\ln I-\ln E, \end{aligned}$$

where

$$\begin{aligned} c_1=\frac{\beta (1-\theta _1)\delta \Lambda }{\left( \mu +\frac{1}{2}\sigma _1^2)^2(\gamma +\alpha +\mu +\frac{1}{2}\sigma _3^2\right) },\ \ c_2=\frac{\beta (1-\theta _1)\delta \Lambda }{\left( \mu +\frac{1}{2}\sigma _1^2)(\gamma +\alpha +\mu +\frac{1}{2}\sigma _3^2\right) ^2}. \end{aligned}$$

Applying Itô’s formula to U, one obtains

$$\begin{aligned} dU=LUdt-c_1\sigma _1dB_1(t)-c_2\sigma _3dB_3(t)-\sigma _2dB_2(t), \end{aligned}$$

where

$$\begin{aligned} LU= & {} -c_1\frac{\Lambda }{S}+c_1\beta (1-\theta _1)I+c_1\beta (1-\theta _1)\theta _2E\nonumber \\&+c_1\mu +\frac{1}{2}c_1\sigma _1^2-c_2\delta \frac{E}{I}\\&+c_2\left( \gamma +\alpha +\mu \right) +\frac{1}{2}c_2\sigma _3^2-\beta (1-\theta _1)\frac{SI}{E}\\&-\beta (1-\theta _1) \theta _2S+\delta +\mu +\frac{1}{2}\sigma _2^2\\\le & {} -3\root 3 \of {c_1c_2\beta (1-\theta _1)\delta \Lambda }+c_1\left( \mu +\frac{1}{2}\sigma _1^2\right) \\&+c_2\left( \gamma +\alpha +\mu +\frac{1}{2}\sigma _3^2\right) +c_1\beta (1-\theta _1)I\\&+c_1\beta (1-\theta _1)\theta _2E+\delta +\mu +\frac{1}{2}\sigma _2^2\\= & {} -\left( \delta +\mu +\frac{1}{2}\sigma _2^2\right) (R_0^s-1)+c_1\beta (1-\theta _1)I+c_1\beta (1-\theta _1)\theta _2E. \end{aligned}$$

Thus

$$\begin{aligned}&dU \le [-(\delta +\mu +\frac{1}{2}\sigma _2^2)(R_0^s-1)+c_1\beta (1-\theta _1)I+c_1\beta (1-\theta _1)\theta _2E]dt\nonumber \\&\quad -c_1\sigma _1dB_1(t)-c_2\sigma _3dB_3(t)-\sigma _2dB_2(t). \end{aligned}$$
(2.8)

Integrating (2.8) over the interval [0, t] and then dividing by t on both sides, we have

$$\begin{aligned} \frac{U(t)-U(0)}{t}\le & {} -\left( \delta +\mu +\frac{1}{2}\sigma _2^2\right) (R_0^s-1)+\frac{c_1\beta (1-\theta _1)}{t}\int ^t_0I(s)ds\nonumber \\+ & {} \frac{c_1\beta (1-\theta _1)\theta _2}{t}\int ^t_0E(s)ds\nonumber \\&\quad -\,c_1\sigma _1t^{-1}\int _0^tdB_1(s)-c_2\sigma _3t^{-1}\int _0^tdB_3(s)-\sigma _2t^{-1}\int _0^tdB_2(s). \nonumber \\ \end{aligned}$$
(2.9)

Taking the superior limit on both sides of (2.9) and combining with (2.6), (2.7) and Lemma 2.2, we have

$$\begin{aligned} \liminf _{t\rightarrow +\infty }\frac{1}{t}\int _0^t I(s)ds \ge \frac{\left( \delta +\mu +\frac{1}{2}\sigma _2^2\right) (R_0^s-1)}{c_1\beta (1-\theta _1) +c_1\beta (1-\theta _1)\theta _2\frac{\gamma +\alpha +\mu }{\delta }}>0. \end{aligned}$$

The proof is complete. \(\square \)

3 Stationary distribution

In this section, we further study the stationary distribution for model (1.3) by using the theory of Hasminskii [61]. Let X(t) be a regular time-homogeneous Markov process in \({\mathbb {R}}^d\) described by

$$\begin{aligned} dX(t)=b(X)dt+\sum _{r=1}^kg_rdB_r(t), \end{aligned}$$

and the corresponding diffusion matrix is defined as follows

$$\begin{aligned} A(X)=(a_{ij}(x)),\ a_{ij}(x)=\sum _{r=1}^kg_r^i(x)g_r^j(x). \end{aligned}$$

Lemma 3.1

[61] The Markov process X(t) has a unique ergodic stationary distribution \(\pi (\cdot )\) if there exists a bounded domain \(U\subset {\mathbb {R}}^d\) with regular bounded \(\Gamma \) and

  1. (i):

    A positive number M satisfied that \(\sum _{i,j=1}^{d}a_{ij}(x)\xi _1\xi _2\ge M|\xi |^2, x\in U, \xi \in {\mathbb {R}}^d \).

  2. (ii):

    There exists V ( V is a nonnegative \(C^2\)-function) such that LV is negative for any \({\mathbb {R}}^d\setminus U\). If \(f(\cdot )\) is a function integrable with respect to the measure \(\pi \), then

    $$\begin{aligned} {\mathbb {P}}_x\left\{ \lim _{T\rightarrow +\infty }\frac{1}{T}\int _0^t f(X(t))dt=\int _{{\mathbb {R}}^d} f(x)\pi (dx)\right\} =1 \end{aligned}$$

    for all \(x\in {\mathbb {R}}^d\).

Theorem 3.1

If Assumption A holds, model (1.3) owns a unique ergodic stationary distribution \(\pi (\cdot )\).

Proof

We only need to verify the assumptions \((i){-}(ii)\) in Lemma 3.1. We first consider the diffusion matrix of model (1.3)

$$\begin{aligned} A=\left( \begin{array}{ccc} \sigma _1^2S^2&{} 0 &{} 0\\ 0 &{} \sigma _2^2E^2 &{} 0\\ 0 &{} 0 &{} \sigma _3^2I^2\\ \end{array} \right) . \end{aligned}$$

Assign \(M=\min _{(S,E,I)\in {\overline{U}}\subset {\mathbb {R}}_+^3}\{\sigma _1^2S^2,\sigma _2^2E^2,\sigma _3^2I^2\}\), then

$$\begin{aligned}&\sum _{i,j=1}^3a_{ij}(S,E,I)\xi _i\xi _j=\sigma _1^2S^2\xi _1^2+\sigma _2^2E^2\xi _2^2+\sigma _3^2I^2\xi _3^3 \ge M|\xi |^2,(S,E,I)\in {\overline{U}},\\&\quad \xi =(\xi _1,\xi _2,\xi _3)\in {\mathbb {R}}^3, \end{aligned}$$

which implies that (i) in Lemma 3.1 is satisfied.

Now, we continue to verify (ii). Consider a \(C^2\)-function \({\tilde{V}}: {\mathbb {R}}_+^3\rightarrow {\mathbb {R}}\) with

$$\begin{aligned} {\tilde{V}}(S,E,I)= & {} {\mathcal {M}}\left( -\ln S-a_1\ln E-a_2\ln I-\frac{\beta (1-\theta _1)\theta _2}{\delta }I\right) \\&+\frac{1}{q+1}(S+E+I)^{q+1}-\ln S-\ln E, \end{aligned}$$

where \(a_1\), \(a_2\) are positive constants to be chosen later, \(0<q<1\) is a constant satisfying \(\kappa :=\mu -\frac{q}{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2)>0\) and the constant \({\mathcal {M}}>0\) is sufficient large such that \(g_1^u+g_2^u-\eta {\mathcal {M}}\le -2\), where \(\eta :=(\mu +\frac{1}{2}\sigma _1^2)(R_0^s-1)\),

$$\begin{aligned} g_1^u= & {} \sup _{S\in (0,+\infty )}\left\{ F-\frac{1}{2}\kappa S^{q+1}-\frac{\Lambda }{S}\right\} ,\ \\ g_2^u= & {} \sup _{E\in (0,+\infty )}\left\{ -\frac{1}{2}\kappa E^{q+1}+\beta (1-\theta _1)\theta _2E\right\} . \end{aligned}$$

In addition, \({\tilde{V}}(S,E,I)\) is continuous and tends to \(+\infty \) when (S, E, I) is close to the boundary of \({\mathbb {R}}_+^3\). Therefore, it has lower bounded and reaches the lower bound at this point \((S_0,E_0,I_0)\) in the interior of \({\mathbb {R}}_+^3\). Let us consider a nonnegative \(C^2\)-function \(V:{\mathbb {R}}_+^3\rightarrow {\mathbb {R}}_+\) with

$$\begin{aligned} V(S,E.I)= & {} {\tilde{V}}(S,E,I)-{\tilde{V}}(S_0,E_0,I_0)\\= & {} {\mathcal {M}}\left( -\ln S-a_1\ln E-a_2\ln I-\frac{\beta (1-\theta _1)\theta _2}{\delta }I\right) \\&+\frac{1}{q+1}(S+E+I)^{q+1}-\ln S\\&-\ln E-{\tilde{V}}(S_0,E_0,I_0)\\= & {} {\mathcal {M}}(V_1+V_2)+V_3+V_4, \end{aligned}$$

where \((S,E,I)\in (\frac{1}{k},k)\times (\frac{1}{k},k)\times (\frac{1}{k},k)\) and \(k>1\) is a sufficiently large integer, \(V_1=-\ln S-a_1\ln E-a_2\ln I,V_2=-\frac{\beta (1-\theta _1)\theta _2}{\delta }I,V_3=\frac{1}{q+1}(S+E+I)^{q+1},V_4=-\ln S-\ln E-{\tilde{V}}(S_0,E_0,I_0)\), and

$$\begin{aligned} a_1= & {} \frac{\beta (1-\theta _1)\delta \Lambda }{\left( \mu +\delta +\frac{1}{2}\sigma _2^2\right) ^2\left( \gamma +\alpha +\mu +\frac{1}{2}\sigma _3^2\right) },\\ a_2= & {} \frac{\beta (1-\theta _1)\delta \Lambda }{\left( \mu +\delta +\frac{1}{2}\sigma _2^2\right) \left( \gamma +\alpha +\mu +\frac{1}{2}\sigma _3^2\right) ^2}. \end{aligned}$$

Applying Itô’s formula, one has

$$\begin{aligned} LV_1= & {} -\frac{\Lambda }{S}+\beta (1-\theta _1)I+\beta (1-\theta _1)\theta _2E\nonumber \\&+\mu +\frac{1}{2}\sigma _1^2-a_1\beta (1-\theta _1)\frac{SI}{E}\nonumber \\&-a_1\beta (1-\theta _1)\theta _2S+a_1\left( \mu +\delta +\frac{1}{2}\sigma _2^2\right) \nonumber \\&-a_2\frac{\delta E}{I}+a_2\left( \gamma +\alpha +\mu +\frac{1}{2}\sigma _3^2\right) \nonumber \\\le & {} -3\root 3 \of {a_1a_2\Lambda \beta (1-\theta _1)\delta }+a_1\left( \mu +\delta +\frac{1}{2}\sigma _2^2\right) \nonumber \\&+a_2\left( \gamma +\alpha +\mu +\frac{1}{2}\sigma _3^2\right) \nonumber \\&+\mu +\frac{1}{2}\sigma _1^2+\beta (1-\theta _1)I+\beta (1-\theta _1)\theta _2E\nonumber \\= & {} -\left( \mu +\frac{1}{2}\sigma _1^2\right) (R_0^s-1)+\beta (1-\theta _1)I+\beta (1-\theta _1)\theta _2E\nonumber \\= & {} -\eta +\beta (1-\theta _1)I+\beta (1-\theta _1)\theta _2E. \end{aligned}$$
(3.1)

Similarly,

$$\begin{aligned} LV_2=-\beta (1-\theta _1)\theta _2E+\frac{\beta (1-\theta _1)\theta _2(\gamma +\alpha +\mu )}{\delta }I, \end{aligned}$$
(3.2)

and

$$\begin{aligned} LV_3= & {} (S+E+I)^q[\Lambda -\mu S-\mu E-(\gamma +\alpha +\mu )I]\nonumber \\&+\frac{q}{2}(S+E+I)^{q-1}(\sigma _1^2S^2+\sigma _2^2E^2+\sigma _3^2I^2)\nonumber \\\le & {} \Lambda (S+E+I)^q-\mu (S+E+I)^{q+1}\nonumber \\&+\frac{q}{2}(S+E+I)^{q-1} (\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2)(S^2+E^2+I^2)\nonumber \\\le & {} \Lambda (S+E+I)^q-\mu (S+E+I)^{q+1}\nonumber \\&+\frac{q}{2}(S+E+I)^{q+1} (\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2)\nonumber \\= & {} \Lambda (S+E+I)^q-\left( \mu -\frac{q}{2}\left( \sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\right) \right) (S+E+I)^{q+1}\nonumber \\= & {} \Lambda (S+E+I)^q-\frac{1}{2}\kappa (S+E+I)^{q+1}-\frac{1}{2}\kappa (S+E+I)^{q+1}\nonumber \\\le & {} Q-\frac{1}{2}\kappa (S+E+I)^{q+1}, \end{aligned}$$
(3.3)

where

$$\begin{aligned} Q=\sup _{(S,E,I)\in {\mathbb {R}}_+^3}\left\{ -\frac{1}{2}\kappa (S+E+I)^{q+1}+\Lambda (S+E+I)^q\right\} . \end{aligned}$$

In addition, we can obtain

$$\begin{aligned} LV_4= & {} -\frac{\Lambda }{S}+\beta (1-\theta _1)I+\beta (1-\theta _1)\theta _2E+\mu +\frac{1}{2}\sigma _1^2\nonumber \\&-\beta (1-\theta _1)\frac{SI}{E}-\beta (1-\theta _1)\theta _2S+\delta +\mu +\frac{1}{2}\sigma _2^2. \end{aligned}$$
(3.4)

Combining with (3.1)–(3.4), we have

$$\begin{aligned} LV\le & {} -\eta {\mathcal {M}}+{\mathcal {M}}\left[ \beta (1-\theta _1)+\frac{\beta (1-\theta _1) \theta _2(\gamma +\alpha +\mu )}{\delta }\right] I+Q\nonumber \\&-\frac{\kappa }{2}(S+E+I)^{q+1}-\frac{\Lambda }{S}+\beta (1-\theta _1)I+\beta (1-\theta _1) \theta _2E\nonumber \\&-\beta (1-\theta _1) \frac{SI}{E}-\beta (1-\theta _1)\theta _2S+2\mu +\delta +\frac{1}{2}\sigma _1^2+\frac{1}{2}\sigma _2^2\nonumber \\\le & {} -\eta {\mathcal {M}}-\frac{1}{2}\kappa I^{q+1}+{\mathcal {M}}\left[ \beta (1-\theta _1) +\frac{\beta (1-\theta _1)\theta _2(\gamma +\alpha +\mu )}{\delta }\right] I\nonumber \\&+\beta (1-\theta _1)I-\frac{1}{2}\kappa E^{q+1}+\beta (1-\theta _1)\theta _2E -\frac{1}{2}\kappa S^{q+1}-\frac{\Lambda }{S}\nonumber \\&-\beta (1-\theta _1)\frac{SI}{E}+Q+2\mu +\delta +\frac{1}{2}\sigma _1^2++\frac{1}{2}\sigma _2^2\nonumber \\= & {} g_1(S)+g_2(E)+g_3(I)-\beta (1-\theta _1)\frac{SI}{E}, \end{aligned}$$
(3.5)

where

$$\begin{aligned} g_1(S)= & {} F-\frac{1}{2}\kappa S^{q+1}-\frac{\Lambda }{S},\\ F= & {} Q+2\mu +\delta +\frac{1}{2}\sigma _1^2+\frac{1}{2}\sigma _2^2,\\ g_2(E)= & {} -\frac{1}{2}\kappa E^{q+1}+\beta (1-\theta _1)\theta _2E,\\ g_3(I)= & {} -\frac{1}{2}\kappa I^{q+1}+{\mathcal {M}}\left\{ -\eta +\left[ \beta (1-\theta _1) +\frac{\beta (1-\theta _1)\theta _2(\gamma +\alpha +\mu )}{\delta }\right] I\right\} \\&+\beta (1-\theta _1)I. \end{aligned}$$

Assign a bounded closed set as follows

$$\begin{aligned} U=\left\{ \varepsilon \le S\le \frac{1}{\varepsilon },\ \varepsilon ^3\le E\le \frac{1}{\varepsilon ^3},\ \varepsilon \le I\le \frac{1}{\varepsilon }\right\} , \end{aligned}$$

where \(\varepsilon >0\) is a suitably small constant satisfying the following inequalities

$$\begin{aligned}&\displaystyle F+g_2^u+g_3^u-\frac{\Lambda }{\varepsilon }\le -1, \end{aligned}$$
(3.6)
$$\begin{aligned}&g_1^u+g_2^u+{\mathcal {M}}\left\{ -\eta +\left[ \beta (1-\theta _1)+\frac{\beta (1-\theta _1) \theta _2(\gamma +\alpha +\mu )}{\delta }\right] \varepsilon \right\} \nonumber \\&\quad +\beta (1-\theta _1)\varepsilon \le -1, \end{aligned}$$
(3.7)
$$\begin{aligned}&g_1^u+g_2^u+g_3^u-\beta (1-\theta _1)\frac{1}{\varepsilon }\le -1, \end{aligned}$$
(3.8)
$$\begin{aligned}&F+g_2^u+g_3^u-\frac{\kappa }{2}\frac{1}{\varepsilon ^{q+1}}\le -1, \end{aligned}$$
(3.9)
$$\begin{aligned}&g_1^u+g_2^u+C_1-\frac{\kappa }{4}\frac{1}{\varepsilon ^{q+1}}\le -1, \end{aligned}$$
(3.10)
$$\begin{aligned}&g_1^u+g_3^u+C_2-\frac{\kappa }{4}\frac{1}{\varepsilon ^{3(q+1)}}\le -1, \end{aligned}$$
(3.11)

where

$$\begin{aligned} g_3^u= & {} \sup _{I\in (0,+\infty )}\left\{ -\frac{1}{2}\kappa I^{q+1}+{\mathcal {M}}\left\{ -\eta +\left[ \beta (1-\theta _1) +\frac{\beta (1-\theta _1)\theta _2(\gamma +\alpha +\mu )}{\delta }\right] I\right\} \right. \\&\left. +\beta (1-\theta _1)I\right\} , \end{aligned}$$

and we will determine the two positive constants \(C_1\), \(C_2\) later. For convenience, we first divide \({\mathbb {R}}_+^3\setminus U\) into six domains with the forms

$$\begin{aligned} U_1= & {} \{(S,E,I)\in {\mathbb {R}}_+^3,0<S<\varepsilon \},\ \ U_2=\{(S,E,I)\in {\mathbb {R}}_+^3,0<I<\varepsilon \},\\ U_3= & {} \{(S,E,I)\in {\mathbb {R}}_+^3,S>\varepsilon ,I>\varepsilon ,0<E<\varepsilon ^3\},\\ U_4= & {} \left\{ (S,E,I)\in {\mathbb {R}}_+^3,S>\frac{1}{\varepsilon }\right\} ,\\ U_5= & {} \left\{ (S,E,I)\in {\mathbb {R}}_+^3,I>\frac{1}{\varepsilon }\right\} ,\ \ U_6=\left\{ (S,E,I)\in {\mathbb {R}}_+^3,E>\frac{1}{\varepsilon ^3}\right\} . \end{aligned}$$

Clearly, \({\mathbb {R}}_+^3\setminus U=U_1\cup U_2\cup U_3\cup U_4\cup U_5\cup U_6\). By verifying the above six cases, we will prove that \(LV(S,E,I)\le -1\) on \({\mathbb {R}}_+^3\setminus U\).

Case 1 When \((S,E,I)\in U_1\), then (3.5) and (3.6) imply that \(LV\le F+g_2^u+g_3^u-\frac{\Lambda }{\varepsilon }\le -1\).

Case 2 When \((S,E,I)\in U_2\), it follows from (3.5) and (3.7) that

$$\begin{aligned} LV\le & {} g_1^u+g_2^u+{\mathcal {M}}\left\{ -\eta +\left[ \beta (1-\theta _1) +\frac{\beta (1-\theta _1)\theta _2(\gamma +\alpha +\mu )}{\delta }\right] \varepsilon \right\} \\&+\beta (1-\theta _1)\varepsilon \le -1. \end{aligned}$$

Case 3 When \((S,E,I)\in U_3\), we obtain from (3.5) and (3.8) that \(LV\le g_1^u+g_2^u+g_3^u-\beta (1-\theta _1)\frac{1}{\varepsilon }\le -1\).

Case 4 When \((S,E,I)\in U_4\), (3.5) and (3.9) imply that \(LV\le F+g_2^u+g_3^u-\frac{\kappa }{2}\frac{1}{\varepsilon ^{q+1}}\le -1\).

Case 5 When \((S,E,I)\in U_5\), it follows from (3.5) and (3.10) that \(LV\le g_1^u+g_2^u+C_1-\frac{\kappa }{4}\frac{1}{\varepsilon ^{q+1}}\le -1\), where

$$\begin{aligned} C_1= & {} \sup _{I\in (0,+\infty )}\Bigg \{-\frac{\kappa }{4}I^{q+1}+{\mathcal {M}}\left\{ -\eta +\left[ \beta (1-\theta _1) +\frac{\beta (1-\theta _1)\theta _2(\gamma +\alpha +\mu )}{\delta }\right] I\right\} \\&+\beta (1-\theta _1)I\Bigg \}. \end{aligned}$$

Case 6 When \((S,E,I)\in U_6\), one obtains from (3.5) and (3.11) that \(LV\le g_1^u+g_3^u+C_2-\frac{\kappa }{4}\frac{1}{\varepsilon ^{3(q+1)}}\le -1\), where \(C_2=\sup _{E\in (0,+\infty )}\{-\frac{\kappa }{4}E^{q+1}+\beta (1-\theta _1)\theta _2E\}\).

From the above discussion, we obtain that \(LV\le -1\) on \({\mathbb {R}}_+^3\setminus U\), which implies that (ii) in Lemma 3.1 also holds. This completes the proof. \(\square \)

4 Numerical simulations

In this section, our analytical results will be verified by numerical simulations. Let us choose initial value \((S(0),E(0),I(0))\!=\!(20,15,10)\), and the parameter values are kept the same as in [38], see Table 2.

Table 2 Parameter values used in model (1.2)
Full size table
Fig. 1
figure 1

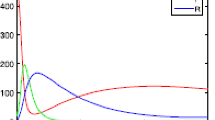
a \(\theta _1=0.7\), \(R_0=1.7619>1\), then the positive equilibrium \(P^*\) of deterministic model (1.2) is globally asymptotically stable. b \(\theta _1=0.9\), \(R_0=0.5873<1\), then its disease-free equilibrium \(P^0\) is globally asymptotically stable

Full size image

\(\bullet \) Jiao et al. [38] discussed the effect of \(\theta _1\) (see Fig. 1a and b), that is, the disease I(t) of deterministic model (1.2) will die out if \(\theta _1\) is large, and however the disease I(t) will be persistent if \(\theta _1\) is relative small. This fact shows that the strategy of the homestead–isolation on the susceptible is very important in the epidemics of infectious diseases.

\(\bullet \) We choose \(\sigma _1=0.4\), \(\sigma _2=3.5\), \(\sigma _3=1.3\) and the same \(\theta _1=0.9\) as Fig. 1b, then \({\hat{R}}_0\approx 0.957823<1\). It follows from Theorem 2.1 that the disease goes to extinction (see Fig. 2). Compared with Fig. 1b, we can see that the noise will accelerate the extinction of the disease although the disease tends to be extinct in deterministic model (1.2).

Fig. 2
figure 2

a The disease of stochastic model (1.3) is extinct. b Frequency histogram at time 100

Full size image

\(\bullet \) To illustrate the threshold of disease and the effect of the environment white noises. To compare with Fig. 1a, we continue to select the same \(\theta _1=0.7\) as Fig. 1a, and smaller noises with \(\sigma _1=0.1\), \(\sigma _2=0.08\), \(\sigma _3=0.05\). For the stochastic model (1.3), a calculation shows that \(R_0^s\approx 1.3952064>1\), then the conditions of Theorems 2.2 and 3.1 are satisfied. As observed in Fig. 3 the disease of model (1.3) goes to strong persistence in the mean, and moreover the conditions support model (1.3) owns an ergodic stationary distribution, see Fig. 4. Recalling Fig. 1a, we know that the disease will persist if \(\theta _1=0.7\), and Figs. 3 and 4 shows that although it is affected by environmental noise, the disease will persist if the noise intensity is relatively low.

Fig. 3
figure 3

a The disease of stochastic model (1.3) will be strongly persistent in the mean. b Frequency histogram at time 100

Full size image
Fig. 4
figure 4

a Solution of stochastic model (1.3). b Blue line frequency histogram of stochastic model (1.3) at time 100; Red line the probability density function (PDF) of its corresponding stationary distribution simulated by 3000 sample trajectories. (Color figure online)

Full size image

5 Discussions

In this paper, based on a deterministic SEIR epidemic model with infectivity in incubation period and homestead–isolation on the susceptible proposed by Jiao et al. [38], we incorporate white noise into the above model and establish a stochastic version. We first discuss the extinction and strong persistence in the mean of the disease, and later the stationary distribution is investigated by using Hasminskiis method and Lyapunov function. Let us recall Theorems 2.1, 2.2 and 3.1, we reveal the biological conclusions as follows:

\(\bullet \) Theorem 2.1 shows that the disease will be extinct when \({\hat{R}}_{0}<1\). This fact implies that if the noise intensities \(\sigma _i^2(i=1,2,3)\) are suitably large and the cooperation from the homestead–isolation rate \(\theta _1\) is enough while the infective rate of the exposed in incubation period \(\theta _2\) is relatively small, then the disease I(t) is extinct. That is, increasing the noise intensity and homestead–isolation rate are advantageous for the extinction of the disease while increasing the infective rate of the exposed in incubation period is harmful for it.

\(\bullet \) It follows from \(R_0^s>1\) (see Theorem 2.2) that if the noise intensities \(\sigma _i^2(i=1,2,3)\) are small and the cooperation from the homestead–isolation rate \(\theta _1\) is inadequate, then the disease I(t) will be strong persistent in the mean.

\(\bullet \) When \(R_0^s>1\), Theorem 3.1 shows that model (1.3) has a unique stationary distribution \(\pi (\cdot )\) which is ergodic. This result indicates that decreasing the noise intensities \(\sigma _i^2(i=1,2,3)\) and the homestead–isolation rate \(\theta _1\) may result in a high prevalence level of the disease, and hence the governments should strictly implement the isolation system to make every effort to curb propagation of disease.

In the end, it should be pointed out that, in order to compare with the global dynamical results of model (1.2) established in [38], this work is only concerned with the stochastic dynamics of the variables S, E, I in model (1.3) under the three noises \({\dot{B}}_i(t)\), \(i=1,2,3\), however it also would deserve to introduce a noise into the variable R in the fourth equation of model (1.1) and investigate the four-dimension stochastic model. In addition, we would like to develop more complicated models by incorporating other forms of stochastic perturbations (e.g., perturbed parameters [23, 52,53,54,55,56]), Lévy jump [14, 45] or regime switching [62], and we leave these interesting and challenging issues for future consideration.