Diploidy and the selective advantage for sexual reproduction in unicellular organisms

Abstract

This article develops mathematical models describing the evolutionary dynamics of both asexually and sexually reproducing populations of diploid unicellular organisms. The asexual and sexual life cycles are based on the asexual and sexual life cycles in Saccharomyces cerevisiae, Baker’s yeast, which normally reproduces by asexual budding, but switches to sexual reproduction when stressed. The mathematical models consider three reproduction pathways: (1) Asexual reproduction, (2) self-fertilization, and (3) sexual reproduction. We also consider two forms of genome organization. In the first case, we assume that the genome consists of two multi-gene chromosomes, whereas in the second case, we consider the opposite extreme and assume that each gene defines a separate chromosome, which we call the multi-chromosome genome. These two cases are considered to explore the role that recombination has on the mutation-selection balance and the selective advantage of the various reproduction strategies. We assume that the purpose of diploidy is to provide redundancy, so that damage to a gene may be repaired using the other, presumably undamaged copy (a process known as homologous recombination repair). As a result, we assume that the fitness of the organism only depends on the number of homologous gene pairs that contain at least one functional copy of a given gene. If the organism has at least one functional copy of every gene in the genome, we assume a fitness of 1. In general, if the organism has l homologous pairs that lack a functional copy of the given gene, then the fitness of the organism is κ _l . The κ _l are assumed to be monotonically decreasing, so that κ₀ = 1 > κ₁ > κ₂ > ⋯ > κ_∞ = 0. For nearly all of the reproduction strategies we consider, we find, in the limit of large N, that the mean fitness at mutation-selection balance is $\hbox{max}\{2 e^{-\mu}-1, 0\} ,$ where N is the number of genes in the haploid set of the genome, ε is the probability that a given DNA template strand of a given gene produces a mutated daughter during replication, and μ = Nε. The only exception is the sexual reproduction pathway for the multi-chromosomed genome. Assuming a multiplicative fitness landscape where κ _l  = α^l for α ∈ (0, 1), this strategy is found to have a mean fitness that exceeds the mean fitness of all the other strategies. Furthermore, while other reproduction strategies experience a total loss of viability due to the steady accumulation of deleterious mutations once μ exceeds $\ln 2 ,$ no such transition occurs in the sexual pathway. Indeed, in the limit as α → 1 for the multiplicative landscape, we can show that the mean fitness for the sexual pathway with the multi-chromosomed genome converges to e ^−2μ, which is always positive. We explicitly allow for mitotic recombination in this study, which, in contrast to previous studies using different models, does not have any advantage over other asexual reproduction strategies. The results of this article provide a basis for understanding the selective advantage of the specific meiotic pathway that is employed by sexually reproducing organisms. The results of this article also suggest an explanation for why unicellular organisms such as Saccharomyces cerevisiae (Baker’s yeast) switch to a sexual mode of reproduction when stressed. While the results of this article are based on modeling mutation-propagation in unicellular organisms, they nevertheless suggest that, in more complex organisms with significantly larger genomes, sex is necessary to prevent the loss of viability of a population due to genetic drift. Finally, and perhaps most importantly, the results of this article demonstrate a selective advantage for sexual reproduction with fewer and much less restrictive assumptions than those of previous studies.

Appendices

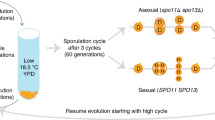
Appendix A: Derivation of the evolutionary dynamics equations for asexual reproduction

Two-chromosomed genome

The dynamical equations governing the evolution of the asexually replicating, two-chromosomed unicellular population, are given by

$$ \begin{aligned} & {\frac{d n_{\{\sigma_1, \sigma_2\}}}{dt}} = -\kappa_{\{\sigma_1, \sigma_2\}} n_{\{\sigma_1, \sigma_2\}} + \sum_{\{\sigma_1^{\prime}, \sigma_2^{\prime}\}} \kappa_{\{\sigma_1^{\prime}, \sigma_2^{\prime}\}} n_{\{\sigma_1^{\prime}, \sigma_2^{\prime}\}} \\ & \times \sum_{\sigma_{11}^{\prime}} \sum_{\sigma_{12}^{\prime}} \sum_{\sigma_{21}^{\prime}} \sum_{\sigma_{22}^{\prime}} p(\sigma_1^{\prime}, \sigma_{11}^{\prime}) p(\sigma_1^{\prime}, \sigma_{12}^{\prime}) p(\sigma_2^{\prime}, \sigma_{21}^{\prime}) p(\sigma_2^{\prime}, \sigma_{22}^{\prime}) \\ & \times \left[r_i (\delta_{\{\sigma_{11}^{\prime}, \sigma_{12}^{\prime}\}, \{\sigma_1, \sigma_2\}} + \delta_{\{\sigma_{21}^{\prime}, \sigma_{22}^{\prime}\}, \{\sigma_1, \sigma_2\}}) \right.\\ & \left.+ {\frac{1}{2}} (1 - r_i) (\delta_{\{\sigma_{11}^{\prime}, \sigma_{21}^{\prime}\}, \{\sigma_1, \sigma_2\}} + \delta_{\{\sigma_{12}^{\prime}, \sigma_{22}^{\prime}\}, \{\sigma_1, \sigma_2\}}) \right.\\ & \left.+ {\frac{1}{2}} (1 - r_i) (\delta_{\{\sigma_{11}^{\prime}, \sigma_{22}^{\prime}\}, \{\sigma_1, \sigma_2\}} + \delta_{\{\sigma_{12}^{\prime}, \sigma_{21}^{\prime}\}, \{\sigma_1, \sigma_2\}})\right] \end{aligned} $$

(58)

where $\delta_{\{\sigma_1, \sigma_2\}, \{\sigma_3, \sigma_4\}} =1$ if $\{\sigma_1, \sigma_2\} =\{\sigma_3, \sigma_4\} ,$ and 0 otherwise.

The above equation may be expanded into separate terms, which may then be collected and simplified to give

$$ \begin{aligned} & {\frac{d n_{\{\sigma_1, \sigma_2\}}}{dt}} = -\kappa_{\{\sigma_1, \sigma_2\}} n_{\{\sigma_1, \sigma_2\}} + r_i \sum_{\{\sigma_1^{\prime}, \sigma_2^{\prime}\}} \kappa_{\{\sigma_1^{\prime}, \sigma_2^{\prime}\}} n_{\{\sigma_1^{\prime}, \sigma_2^{\prime}\}} \\ & \times\sum_{(\sigma_1^{\prime\prime}, \sigma_2^{\prime\prime}), \{\sigma_1^{\prime\prime}, \sigma_2^{\prime\prime}\} = \{\sigma_1, \sigma_2\}} \left[p(\sigma_1^{\prime}, \sigma_1^{\prime\prime}) p(\sigma_1^{\prime}, \sigma_2^{\prime\prime}) + p(\sigma_2^{\prime}, \sigma_1^{\prime\prime}) p(\sigma_2^{\prime}, \sigma_2^{\prime\prime})\right] \\ & + 2 (1 - r_i) \sum_{\{\sigma_1^{\prime}, \sigma_2^{\prime}\}} \kappa_{\{\sigma_1^{\prime}, \sigma_2^{\prime}\}} n_{\{\sigma_1^{\prime}, \sigma_2^{\prime}\}} \sum_{(\sigma_1^{\prime\prime}, \sigma_2^{\prime\prime}), \{\sigma_1^{\prime\prime}, \sigma_2^{\prime\prime}\} = \{\sigma_1, \sigma_2\}} p(\sigma_1^{\prime}, \sigma_1^{\prime\prime}) p(\sigma_2^{\prime}, \sigma_2^{\prime\prime}) \end{aligned} $$

(59)

Converting to the ordered strand-pair representation we have, for σ₁ ≠ σ₂,

$$ \begin{aligned} & {\frac{d n_{(\sigma_1, \sigma_2)}}{dt}} = -\kappa_{(\sigma_1, \sigma_2)} n_{(\sigma_1, \sigma_2)} + 2 r_i \sum_{\{\sigma_1^{\prime}, \sigma_2^{\prime}\}, \sigma_1^{\prime} \neq \sigma_2^{\prime}} \kappa_{(\sigma_1^{\prime}, \sigma_2^{\prime})} n_{(\sigma_1^{\prime}, \sigma_2^{\prime})} \\ & \times[p(\sigma_1^{\prime}, \sigma_1) p(\sigma_1^{\prime}, \sigma_2) + p(\sigma_2^{\prime}, \sigma_1) p(\sigma_2^{\prime}, \sigma_2)] \\ & + 2 r_i \sum_{\{\sigma^{\prime}, \sigma^{\prime}\}} \kappa_{(\sigma^{\prime}, \sigma^{\prime})} n_{(\sigma^{\prime}, \sigma^{\prime})} p(\sigma^{\prime}, \sigma_1) p(\sigma^{\prime}, \sigma_2) \\ & + 2 (1 - r_i) \sum_{\{\sigma_1^{\prime}, \sigma_2^{\prime}\}, \sigma_1^{\prime} \neq \sigma_2^{\prime}} \kappa_{(\sigma_1^{\prime}, \sigma_2^{\prime})} n_{(\sigma_1^{\prime}, \sigma_2^{\prime})} [p(\sigma_1^{\prime}, \sigma_1) p(\sigma_2^{\prime}, \sigma_2) + p(\sigma_2^{\prime}, \sigma_1) p(\sigma_1^{\prime}, \sigma_2)] \\ & + 2 (1 - r_i) \sum_{\{\sigma^{\prime}, \sigma^{\prime}\}} \kappa_{(\sigma^{\prime}, \sigma^{\prime})} n_{(\sigma^{\prime}, \sigma^{\prime})} p(\sigma^{\prime}, \sigma_1) p(\sigma^{\prime}, \sigma_2) \\ & = -\kappa_{(\sigma_1, \sigma_2)} n_{(\sigma_1, \sigma_2)} + 2 r_i \sum_{(\sigma_1^{\prime}, \sigma_2^{\prime})} \kappa_{(\sigma_1^{\prime}, \sigma_2^{\prime})} n_{(\sigma_1^{\prime}, \sigma_2^{\prime})} p(\sigma_1^{\prime}, \sigma_1) p(\sigma_1^{\prime}, \sigma_2) \\ & + 2 (1 - r_i) \sum_{(\sigma_1^{\prime}, \sigma_2^{\prime})} \kappa_{(\sigma_1^{\prime}, \sigma_2^{\prime})} n_{(\sigma_1^{\prime}, \sigma_2^{\prime})} p(\sigma_1^{\prime}, \sigma_1) p(\sigma_2^{\prime}, \sigma_2) \\ \end{aligned} $$

(60)

We also have

$$ \begin{aligned} & {\frac{d n_{(\sigma, \sigma)}}{dt}} = -\kappa_{(\sigma, \sigma)} n_{(\sigma, \sigma)} + 2 r_i \sum_{\{\sigma_1^{\prime}, \sigma_2^{\prime}\}, \sigma_1^{\prime} \neq \sigma_2^{\prime}} \kappa_{(\sigma_1^{\prime}, \sigma_2^{\prime})} n_{(\sigma_1^{\prime}, \sigma_2^{\prime})} \\ & [p(\sigma_1^{\prime}, \sigma) p(\sigma_1^{\prime}, \sigma) + p(\sigma_2^{\prime}, \sigma) p(\sigma_2^{\prime}, \sigma)] \\ & + 2 r_i \sum_{\{\sigma^{\prime}, \sigma^{\prime}\}} \kappa_{(\sigma^{\prime}, \sigma^{\prime})} n_{(\sigma^{\prime}, \sigma^{\prime})} p(\sigma^{\prime}, \sigma) p(\sigma^{\prime}, \sigma) \\ & + 2 (1 - r_i) \sum_{\{\sigma_1^{\prime}, \sigma_2^{\prime}\}, \sigma_1^{\prime} \neq \sigma_2^{\prime}} \kappa_{(\sigma_1^{\prime}, \sigma_2^{\prime})} n_{(\sigma_1^{\prime}, \sigma_2^{\prime})} [p(\sigma_1^{\prime}, \sigma) p(\sigma_2^{\prime}, \sigma) + p(\sigma_2^{\prime}, \sigma) p(\sigma_1^{\prime}, \sigma)] \\ & + 2 (1 - r_i) \sum_{\{\sigma^{\prime}, \sigma^{\prime}\}} \kappa_{(\sigma^{\prime}, \sigma^{\prime})} n_{(\sigma^{\prime}, \sigma^{\prime})} p(\sigma^{\prime}, \sigma) p(\sigma^{\prime}, \sigma) \\ & = -\kappa_{(\sigma, \sigma)} n_{(\sigma, \sigma)} + 2 r_i \sum_{(\sigma_1^{\prime}, \sigma_2^{\prime})} \kappa_{(\sigma_1^{\prime}, \sigma_2^{\prime})} n_{(\sigma_1^{\prime}, \sigma_2^{\prime})} p(\sigma_1^{\prime}, \sigma) p(\sigma_2^{\prime}, \sigma) \\ & + 2 (1 - r_i) \sum_{(\sigma_1^{\prime}, \sigma_2^{\prime})} \kappa_{(\sigma_1^{\prime}, \sigma_2^{\prime})} n_{(\sigma_1^{\prime}, \sigma_2^{\prime})} p(\sigma_1^{\prime}, \sigma) p(\sigma_2^{\prime}, \sigma) \\ \end{aligned} $$

(61)

and so, converting from population numbers to population fractions, we obtain,

$$ \begin{aligned} & {\frac{d x_{(\sigma_1, \sigma_2)}}{dt}} = -(\kappa_{(\sigma_1, \sigma_2)} + \bar{\kappa}(t)) x_{(\sigma_1, \sigma_2)} \\ & + 2 r_i \sum_{(\sigma_1^{\prime}, \sigma_2^{\prime})} \kappa_{(\sigma_1^{\prime}, \sigma_2^{\prime})} x_{(\sigma_1^{\prime}, \sigma_2^{\prime})} p(\sigma_1^{\prime}, \sigma_1) p(\sigma_1^{\prime}, \sigma_2) \\ & + 2 (1 - r_i) \sum_{(\sigma_1^{\prime}, \sigma_2^{\prime})} \kappa_{(\sigma_1^{\prime}, \sigma_2^{\prime})} x_{(\sigma_1^{\prime}, \sigma_2^{\prime})} p(\sigma_1^{\prime}, \sigma_1) p(\sigma_2^{\prime}, \sigma_2) \end{aligned} $$

(62)

where $x_{({\sigma_1,}\sigma_2)} {\equiv}n_{({\sigma_1,}\sigma_2)}/(n =\sum_{(\sigma_1^{\prime}, \sigma_2^{\prime})} n_{(\sigma_1^{\prime}, \sigma_2^{\prime})}) ,$ and $\bar{\kappa}(t) = (1/n) (dn/dt) = \sum_{(\sigma_1, \sigma_2)} \kappa_{(\sigma_1, \sigma_2)} x_{(\sigma_1, \sigma_2)} .$

In order to convert this to a set of equations in terms of the $z_{l_{10}, l_{01}, l_{00}}$ population fractions, we proceed as follows: Given a daughter-ordered strand-pair (σ₁, σ₂) characterized by the parameters, l ₁₀, l ₀₁, l ₀₀, and given a parent-ordered strand-pair (σ′₁, σ′₂), we let $l_{i_1 i_2 j_1 j_2}$ denote the number of positions where σ₁ is i ₁, σ₂ is i ₂, σ′₁ is j ₁, and σ′₂ is j ₂. We then have,

$$ \begin{aligned} & p(\sigma_1^{\prime}, \sigma_1) = p^{l_{1111} + l_{1110} + l_{1011} + l_{1010}} (1 - p)^{l_{0111} + l_{0110} + l_{0011} + l_{0010}} \delta_{l_{1101} + l_{1100} + l_{1001} + l_{1000}, 0} \\ & p(\sigma_1^{\prime}, \sigma_2) = p^{l_{1111} + l_{1110} + l_{0111} + l_{0110}} (1 - p)^{l_{1011} + l_{1010} + l_{0011} + l_{0010}} \delta_{l_{1101} + l_{1100} + l_{0101} + l_{0100}, 0} \\ & p(\sigma_2^{\prime}, \sigma_2) = p^{l_{1111} + l_{1101} + l_{0111} + l_{0101}} (1 - p)^{l_{1011} + l_{1001} + l_{0011} + l_{0001}} \delta_{l_{1110} + l_{1100} + l_{0110} + l_{0100}, 0} \end{aligned} $$

(63)

Taking into account degeneracies, we then have

$$ \begin{aligned} & {\frac{d z_{l_{10}, l_{01}, l_{00}}}{dt}} = -(\kappa_{l_{00}} + \bar{\kappa}(t)) z_{l_{10}, l_{01}, l_{00}} + 2 r_i {\frac{N!}{l_{10}! l_{01}! l_{00}! (N - l_{10} - l_{01} - l_{00})!}} \\ & \times \sum_{l_{1110} = 0}^{N - l_{10} - l_{01} - l_{00}} \sum_{l_{1101} = 0}^{N - l_{10} - l_{01} - l_{00} - l_{1110}} \sum_{l_{1100} = 0}^{N - l_{10} - l_{01} - l_{00} - l_{1110} - l_{1101}} \sum_{l_{1010} = 0}^{l_{10}} \sum_{l_{1001} = 0}^{l_{10} - l_{1010}} \sum_{l_{1000} = 0}^{l_{10} - l_{1010} - l_{1001}} \\ & \sum_{l_{0110} = 0}^{l_{01}} \sum_{l_{0101} = 0}^{l_{01} - l_{0110}} \sum_{l_{0100} = 0}^{l_{01} - l_{0110} - l_{0101}} \sum_{l_{0010} = 0}^{l_{00}} \sum_{l_{0001} = 0}^{l_{00} - l_{0010}} \sum_{l_{0000} = 0}^{l_{00} - l_{0010} - l_{0001}} \kappa_{l_{1100} + l_{1000} + l_{0100} + l_{0000}} \\ & \times\frac{z_{l_{1110} + l_{1010} + l_{0110} + l_{0010}, l_{1101} + l_{1001} + l_{0101} + l_{0001}, l_{1100} + l_{1000} + l_{0100} + l_{0000}}}{\left( \begin{array}{l} N\\ l_{1110} + l_{1010} + l_{0110} + l_{0010}\\ \end{array}\right) \left(\begin{array}{l}N - l_{1110} - l_{1010} - l_{0110} - l_{0010}\\ l_{1101} + l_{1001} + l_{0101} + l_{0001}\\ \end{array}\right) \left(\begin{array}{l} N - l_{1110} - l_{1010} - l_{0110} - l_{0010} - l_{1101} - l_{1001} - l_{0101} - l_{0001}\\ l_{1100} + l_{1000} + l_{0100} + l_{0000}\end{array}\right)}\\ & \times {\left(\begin{array}{l} N - l_{10} - l_{01} - l_{00}\\ l_{1110}\\ \end{array}\right) \left(\begin{array}{l} N - l_{10} - l_{01} - l_{00} - l_{1110}\\ l_{1101}\\ \end{array}\right) \left(\begin{array}{l} N - l_{10} - l_{01} - l_{00} - l_{1110} - l_{1101}\\ l_{1100}\\ \end{array}\right)} \\ & \times {\left(\begin{array}{l}l_{10}\\ l_{1010}\\ \end{array}\right) \left(\begin{array}{l}l_{10} - l_{1010}\\ l_{1001}\\ \end{array}\right) \left(\begin{array}{l}l_{10} - l_{1010} - l_{1001}\\ l_{1000}\\ \end{array}\right) \left(\begin{array}{l}l_{01}\\ l_{0110}\\ \end{array}\right) \left(\begin{array}{l}l_{01} - l_{0110}\\ l_{0101}\\ \end{array}\right) \left(\begin{array}{l}l_{01} - l_{0110} - l_{0101}\\ l_{0100}\\ \end{array}\right)}\\ & \times {\left(\begin{array}{l} l_{00}\\ l_{0010}\\ \end{array}\right) \left(\begin{array}{l} l_{00} - l_{0010}\\ l_{0001}\\ \end{array}\right) \left(\begin{array}{l} l_{00} - l_{0010} - l_{0001}\\ l_{0000}\\ \end{array}\right)} \\ & \times p^{l_{1111} + l_{1110} + l_{1011} + l_{1010}} (1 - p)^{l_{0111} + l_{0110} + l_{0011} + l_{0010}} \delta_{l_{1101} + l_{1100} + l_{1001} + l_{1000}, 0} \\ & \times p^{l_{1111} + l_{1110} + l_{0111} + l_{0110}} (1 - p)^{l_{1011} + l_{1010} + l_{0011} + l_{0010}} \delta_{l_{1101} + l_{1100} + l_{0101} + l_{0100}, 0} \\ & + 2 (1 - r_i) {\frac{N!}{l_{10}! l_{01}! l_{00}! (N - l_{10} - l_{01} - l_{00})!}} \\ & \times \sum_{l_{1110} = 0}^{N - l_{10} - l_{01} - l_{00}} \sum_{l_{1101} = 0}^{N - l_{10} - l_{01} - l_{00} - l_{1110}} \sum_{l_{1100} = 0}^{N - l_{10} - l_{01} - l_{00} - l_{1110} - l_{1101}} \sum_{l_{1010} = 0}^{l_{10}} \sum_{l_{1001} = 0}^{l_{10} - l_{1010}} \sum_{l_{1000} = 0}^{l_{10} - l_{1010} - l_{1001}} \\ & \sum_{l_{0110} = 0}^{l_{01}} \sum_{l_{0101} = 0}^{l_{01} - l_{0110}} \sum_{l_{0100} = 0}^{l_{01} - l_{0110} - l_{0101}} \sum_{l_{0010} = 0}^{l_{00}} \sum_{l_{0001} = 0}^{l_{00} - l_{0010}} \sum_{l_{0000} = 0}^{l_{00} - l_{0010} - l_{0001}} \kappa_{l_{1100} + l_{1000} + l_{0100} + l_{0000}} \\ & \times \frac{z_{l_{1110} + l_{1010} + l_{0110} + l_{0010}, l_{1101} + l_{1001} + l_{0101} + l_{0001}, l_{1100} + l_{1000} + l_{0100} + l_{0000}}} {\left(\begin{array}{l}N\\ l_{1110} + l_{1010} + l_{0110} + l_{0010}\\ \end{array}\right) \left(\begin{array}{l}N - l_{1110} - l_{1010} - l_{0110} - l_{0010}\\ l_{1101} + l_{1001} + l_{0101} + l_{0001}\\ \end{array}\right) \left(\begin{array}{l} N - l_{1110} - l_{1010} - l_{0110} - l_{0010} - l_{1101} - l_{1001} - l_{0101} - l_{0001}\\ l_{1100} + l_{1000} + l_{0100} + l_{0000}\end{array}\right)} \\ & \times {\left(\begin{array}{l} N - l_{10} - l_{01} - l_{00}\\ l_{1110}\\ \end{array}\right) \left(\begin{array}{l} N - l_{10} - l_{01} - l_{00} - l_{1110}\\ l_{1101}\\ \end{array}\right) \left(\begin{array}{l} N - l_{10} - l_{01} - l_{00} - l_{1110} - l_{1101}\\ l_{1100}\\ \end{array}\right) } \\ & \times {\left(\begin{array}{l}l_{10}\\ l_{1010}\\ \end{array}\right) \left(\begin{array}{l}l_{10} - l_{1010}\\ l_{1001}\\ \end{array}\right) \left(\begin{array}{l}l_{10} - l_{1010} - l_{1001}\\ l_{1000}\\ \end{array}\right) \left(\begin{array}{l}l_{01}\\ l_{0110}\\ \end{array}\right) \left(\begin{array}{l}l_{01} - l_{0110}\\ l_{0101}\\ \end{array}\right) \left(\begin{array}{l}l_{01} - l_{0110} - l_{0101}\\ l_{0100}\\ \end{array}\right)}\\ & \times {\left(\begin{array}{l} l_{00}\\ l_{0010}\\ \end{array}\right) \left(\begin{array}{l} l_{00} - l_{0010}\\ l_{0001}\\ \end{array}\right) \left(\begin{array}{l} l_{00} - l_{0010} - l_{0001}\\ l_{0000}\\ \end{array}\right)}\\ & \times p^{l_{1111} + l_{1110} + l_{1011} + l_{1010}} (1 - p)^{l_{0111} + l_{0110} + l_{0011} + l_{0010}} \delta_{l_{1101} + l_{1100} + l_{1001} + l_{1000}, 0} \\ & \times p^{l_{1111} + l_{1101} + l_{0111} + l_{0101}} (1 - p)^{l_{1011} + l_{1001} + l_{0011} + l_{0001}} \delta_{l_{1110} + l_{1100} + l_{0110} + l_{0100}, 0} \\ \end{aligned} $$

After some manipulations, we obtain that

$$ \begin{aligned} & {\frac{d z_{l_{10}, l_{01}, l_{00}}}{dt}} = -(\kappa_{l_{00}} + \bar{\kappa}(t)) z_{l_{10}, l_{01}, l_{00}} + 2 r_i \sum_{l_{1110} = 0}^{N - l_{10} - l_{01} - l_{00}} \sum_{l_{1010} = 0}^{l_{10}} \sum_{l_{0110} = 0}^{l_{01}} \sum_{l_{0010} = 0}^{l_{00}} \sum_{l_{0001} = 0}^{l_{00} - l_{0010}} \sum_{l_{0000} = 0}^{l_{00} - l_{0010} - l_{0001}} \kappa_{l_{0000}} \\ & \times z_{l_{1110} + l_{1010} + l_{0110} + l_{0010}, l_{0001}, l_{0000}} {\frac{(l_{1110} + l_{1010} + l_{0110} + l_{0010})!}{l_{1110}! l_{1010}! l_{0110}! l_{0010}!}} (1 - \epsilon)^{2 l_{1110}} [\epsilon (1 - \epsilon)]^{l_{1010}} [\epsilon (1 - \epsilon)]^{l_{0110}} \epsilon^{2 l_{0010}} \\ & \times {\frac{(N - l_{1110} - l_{1010} - l_{0110} - l_{0010} - l_{0001} - l_{0000})!}{(l_{10} - l_{1010})! (l_{01} - l_{0110})! (l_{00} - l_{0010} - l_{0001} - l_{0000})! (N - l_{10} - l_{01} - l_{00} - l_{1110})!}} \\ & \times [\epsilon (1 - \epsilon)]^{l_{10} - l_{1010}} [\epsilon (1 - \epsilon)]^{l_{01} - l_{0110}} \epsilon^{2 (l_{00} - l_{0010} - l_{0001} - l_{0000})} (1 - \epsilon)^{2 (N - l_{10} - l_{01} - l_{00} - l_{1110})} \\ & + 2 (1 - r_i) \sum_{l_{1010} = 0}^{l_{10}} \sum_{l_{0101} = 0}^{l_{01}} \sum_{l_{0010} = 0}^{l_{00}} \sum_{l_{0001} = 0}^{l_{00} - l_{0010}} \sum_{l_{0000} = 0}^{l_{00} - l_{0010} - l_{0001}} \kappa_{l_{0000}} z_{l_{1010} + l_{0010}, l_{0101} + l_{0001}, l_{0000}} \\ & \times {\frac{(l_{1010} + l_{0010})!}{l_{1010}! l_{0010}!}} (1 - \epsilon)^{l_{1010}} \epsilon^{l_{0010}} {\frac{(l_{0101} + l_{0001})!}{l_{0101}! l_{0001}!}} (1 - \epsilon)^{l_{0101}} \epsilon^{l_{0001}} \\ & \times {\frac{(N - l_{1010} - l_{0101} - l_{0010} - l_{0001} - l_{0000})!}{(l_{10} - l_{1010})! (l_{01} - l_{0101})! (l_{00} - l_{0010} - l_{0001} - l_{0000})! (N - l_{10} - l_{01} - l_{00})!}} \\ & \times [\epsilon (1 - \epsilon)]^{l_{10} - l_{1010}} [\epsilon (1 - \epsilon)]^{l_{01} - l_{0101}} \epsilon^{2 (l_{00} - l_{0010} - l_{0001} - l_{0000})} (1 - \epsilon)^{2 (N - l_{10} - l_{01} - l_{00})} \\ \end{aligned} $$

(64)

which is equivalent to Eq. 1.

Multi-chromosomed genome

In order to derive the evolutionary dynamics equations for the multi-chromosomed genomes reproducing asexually, we label each of the daughter cells from a given parent as a “left” cell and a “right” cell. We then first wish to determine the probability that a given daughter cell, either left or right, has a particular genome. As the homologous pairs segregate into the daughter cells independently of one another, we may compute the probability of a given segregation pattern for each homologous pair, and then multiply the appropriate probabilities together for a given daughter genome.

For this analysis, we will consider the left daughter cells only, since the arguments are analogous for the right daughter cells. Then, we wish to compute the probability p(rs → xy), where rs, xy = 11, 10, 00, which is the probability that a homologous pair, in which one gene is of type r and the other gene is of type s, produces the homologous pair xy in the left daughter cell. We handle each case in turn:

$\underline{ 11 \rightarrow 11}$: As each daughter chromosome is the daughter of a 1 parent, the probability that a given daughter chromosome is 1 is p, so the probability that both are 1 is p ².

$\underline {11 \rightarrow 10}$: The probability that a given daughter chromosome is 1 is p, and the probability that a daughter chromosome is 0 is 1 − p. As it does not matter which daughter is 1 and which is 0, we obtain an overall probability of 2p (1 − p).

$\underline{11 \rightarrow 00}$: The probability for this pathway is (1 − p)².

$\underline{ 10 \rightarrow 11}$: The 0 parent always forms two 0 daughters, while the 1 parent may form either a 11, 10, or a 00 daughter pair. In order to form a 11 daughter cell, the 1 parent must produce a 11 daughter pair, which occurs with probability p ². Furthermore, the two 1 daughters must co-segregate. As they are derived from the same parent, this occurs with probability r _i . Finally, the two co-segregating 1 daughters must co-segregate into the left cell, which occurs with probability of 1/2. The overall probability is then r _i p ²/2.

$\underline{ 10 \rightarrow 10}$: If the 1 parent forms two 1 daughters, then the two 1 daughters cannot co-segregate, as, otherwise, this would produce a 11 pair in one cell and a 00 pair in the other cell. Therefore, we want each 1 to co-segregate with a 0 derived from the other parent gene, which occurs with probability 1 − r _i . The probability of this particular segregation pattern is (1 − r _i )p ².

The 1 parent forms one 1 and one 0 daughter with probability 2p(1 − p). This produces a 10 pair in one cell, and a 00 pair in the other cell, so the probability that the left cell receives the 10 pair is 1/2, giving an overall probability of p(1 − p).

Adding the probabilities together, we obtain an overall probability of p(1 − r _i p).

$\underline{ 10 \rightarrow 00}$: The probability for this pathway is 1 − p(1 − r _i p) − r _i p ²/2 = 1 − p(1 − r _i p + r _i p/2) = 1 − p(1 − r _i p/2).

$\underline{ 00 \rightarrow 00}$: The probability for this pathway is 1.

Given a daughter diploid characterized by the parameters l ₁₀, l ₀₀, and given a parent diploid, let $l_{i_1 i_2 j_1 j_2}$ denote the number of homologous gene pairs where the daughter is i ₁, i ₂ and the parent is j ₁, j ₂. The probability that the parent diploid produces the daughter diploid as the left daughter is,

$$ p^{2 l_{1111}} [2 p (1 - p)]^{l_{1011}} (1 - p)^{2 l_{0011}} \left({\frac{r_i}{2}} p^2\right)^{l_{1110}} [p (1 - r_i p)]^{l_{1010}} \left[1 - p \left(1 - {\frac{r_i}{2}} p \right)\right]^{l_{0010}} \delta_{l_{1100} + l_{1000}, 0} $$

(65)

Taking into account degeneracies, we obtain that the evolutionary dynamics equations are then,

$$ \begin{aligned} & {\frac{d z_{l_{10}, l_{00}}}{dt}} = -(\kappa_{l_{00}} + \bar{\kappa}(t)) z_{l_{10}, l_{00}} + 2 {\frac{N!}{l_{10}! l_{00}! (N - l_{10} - l_{00})!}} \\ & \times \sum_{l_{1110} = 0}^{N - l_{10} - l_{00}} \sum_{l_{1100} = 0}^{N - l_{10} - l_{00} - l_{1110}} \sum_{l_{1010} = 0}^{l_{10}} \sum_{l_{1000} = 0}^{l_{10} - l_{1010}} \sum_{l_{0010} = 0}^{l_{00}} \sum_{l_{0000} = 0}^{l_{00} - l_{0010}} \kappa_{l_{1100} + l_{1000} + l_{0000}} \\ & \times {\frac{z_{l_{1110} + l_{1010} + l_{0010}, l_{1100} + l_{1000} + l_{0000}}} {{\left(\begin{array}{l} N\\ l_{1110} + l_{1010} + l_{0010}\\ \end{array}\right)} {\left(\begin{array}{l} N - l_{1110} - l_{1010} - l_{0010}\\ l_{1100} + l_{1000} + l_{0000}\\ \end{array}\right)}}} \\ & \times {\left(\begin{array}{l} N - l_{10} - l_{00}\\ l_{1110}\\ \end{array}\right)} {\left(\begin{array}{l} N - l_{10} - l_{00} - l_{1110}\\ l_{1100}\\ \end{array}\right)} {\left(\begin{array}{l} l_{10}\\ l_{1010}\\ \end{array}\right)} {\left(\begin{array}{l} l_{10} - l_{1010}\\ l_{1000}\\ \end{array}\right)} {\left(\begin{array}{l}l_{00}\\ l_{0010}\\ \end{array}\right)} {\left(\begin{array}{l} l_{00} - l_{0010}\\ l_{0000}\\ \end{array}\right)}\\ & \times p^{2 l_{1111}} [2 p (1 - p)]^{l_{1011}} (1 - p)^{2 l_{0011}} ({\frac{r_i}{2}} p^2)^{l_{1110}} [p(1 - r_i p)]^{l_{1010}} \left[1 - p \left(1 - {\frac{r_i}{2}} p\right)\right]^{l_{0010}} \delta_{l_{1100} + l_{1000},0}\\ & = -(\kappa_{l_{00}} + \bar{\kappa}(t)) z_{l_{10}, l_{00}} + 2 \sum_{l_{1110} = 0}^{N - l_{10} - l_{00}} \sum_{l_{1010} = 0}^{l_{10}} \sum_{l_{0010} = 0}^{l_{00}} \sum_{l_{0000} = 0}^{l_{00} - l_{0010}} \kappa_{l_{0000}} z_{l_{1110} + l_{1010} + l_{0010}, l_{0000}} \\ & \times {\frac{(l_{1110} + l_{1010} + l_{0010})!}{l_{1110}! l_{1010}! l_{0010}!}} \left[{\frac{r_i}{2}} (1 - \epsilon)^2\right]^{l_{1110}} [1 - \epsilon - r_i (1 - \epsilon)^2]^{l_{1010}} \left[\epsilon + {\frac{r_i} {2}} (1 - \epsilon)^2\right]^{l_{0010}} \\ & \times {\frac{(N - l_{1110} - l_{1010} - l_{0010} - l_{0000})!}{(l_{10} - l_{1010})! (l_{00} - l_{0010} - l_{0000})! (N - l_{10} - l_{00} - l_{1110})!}} \\ & \times [2 \epsilon (1 - \epsilon)]^{l_{10} - l_{1010}} \epsilon^{2 (l_{00} - l_{0010} - l_{0000})} (1 - \epsilon)^{2 (N - l_{10} - l_{00} - l_{1110})} \\ \end{aligned} $$

(66)

which is identical to Eq. 15.

Appendix B: Derivation of the evolutionary dynamics equations for self-fertilization for the multi-chromosomed genome

In order to develop the evolutionary dynamics equations for self-fertilization with random mating, we proceed as follows: Given a parent diploid cell, we assume that it splits into a left diploid and a right diploid. The left diploid then splits into two haploids, haploid 1 on the left and haploid 2 on the right, while the right diploid also splits into two haploids, haploid 3 on the left and haploid 4 on the right.

We then have the following pairings, all with equal probability because of random mating: (1) 1 ↔ 2, 3 ↔ 4. (2) 1 ↔ 3, 2 ↔ 4. (3) 1 ↔ 4, 2 ↔ 3. Each of the three possible pairing schemes have a probability of 1/3 of occurrence.

We may consider each pairing scheme in turn. Our goal is to determine, for a given parent diploid, the probability of obtaining a specific daughter diploid as the left daughter cell.

We consider the various probabilities in order.

$$ 1 \leftrightarrow 2, 3 \leftrightarrow 4 $$

$\underline{ 11 \rightarrow 11}$: If a homologous pair in the parent diploid is 11, then each daughter gene in the final left diploid is the daughter of a 1 parent. As the probability that a given daughter of a 1 parent is itself 1 is p, the probability that both daughters are 1 is p ².

$\underline{ 11 \rightarrow 10}$: As with the previous case, the probability that a given daughter of a 1 parent is itself 1 is p, while the probability that the daughter is 0 is 1 − p. Therefore, the probability that a given daughter of a 1 parent is 1 and the other daughter of a 1 parent is 0 is p(1 − p). As it does not matter which daughter is 1 and which is 0, we obtain a total probability of 2p(1 − p).

$\underline{ 11 \rightarrow 00}$: The probability of this pathway is 1 − p ² − 2p(1 − p) = (1 − p)².

$\underline{ 10 \rightarrow 11}$: The probability that a 10 pair produces two 1 daughters and two 0 daughters is p ². As these two 1 daughters are from the same 1 parent, the probability that they co-segregate into the left diploid is r _i /2, giving a total probability of r _i p ²/2.

$\underline{ 10 \rightarrow 10}$: The probability that a 10 pair produces 2 1 daughters and 2 0 daughters is p ². As these two 1 daughters are from the same 1 parent, and since the two 0 daughters are from the same 0 parent, the only way to obtain a 10 left daughter cell is for the daughter chromosomes of a given parent not to co-segregate. As this occurs with probability 1 − r _i , we obtain an overall probability of (1 − r _i )p ².

The probability that a 10 pair produces 1 1 daughter and 3 0 daughters is 2 p(1 − p). As the probability that the 1 chromosome ends up in the left daughter cell is 1/2, we obtain an overall probability of p(1 − p).

The total probability is then (1 − r _i )p ² + p(1 − p) = p(1 − r _i p).

$\underline{10 \rightarrow 00 }$: The probability for this pathway is 1 − r _i p ²/2 − p(1 − r _i p) = 1 − p(1 − r _i p/2).

$\underline{00 \rightarrow 00}$: Because of the neglect of backmutations, this occurs with probability 1.

$$ 1 \leftrightarrow 3, 2 \leftrightarrow 4 $$

$\underline{11 \rightarrow 11, 10, 00 }$: Adopting a similar line of reasoning to the one used above, we obtain an identical corresponding set of transition probabilities.

$\underline{10 \rightarrow 11}$: The 1 parent must produce two 1 daughters with probability p ². These 1 daughters must segregate into distinct diploids, with a probability of 1 − r _i . The probability that these 1 daughters then end up in haploids 1 and 3, respectively, is 1/4, for a total probability of (1 − r _i )p ²/4.

$\underline{10 \rightarrow 10}$: The 1 parent produces two 1 daughters with probability p ², while the 0 parent produces two 0 daughters with probability 1. If the 1 daughters and the 0 daughters each co-segregate, which occurs with probability r _i , then the 1 haploid and the 3 haploid will together form a 10 pair. If the daughters of each parent do not co-segregate, with probability 1 − r _i , then we form two 10 diploids. The probability that the 1 haploid has a 1 and the 3 haploid a 0 is 1/4, and the probability that the 1 haploid has a 0 and the 3 haploid a 1 is 1/4, giving an overall probability of p ²(r _i  + (1 − r _i )/2) = (1 + r _i ) p ²/2.

The 1 parent produces one 1 daughter and one 0 daughter with probability 2p(1 − p). The probability that this 1 daughter ends up in either haploid 1 or 3 is 1/2, for an overall probability of p(1 − p).

The total probability is then p[1 − p + (1 + r _i )p/2] = p [1 − (1 − r _i )p/2].

$\underline{10 \rightarrow 00}$: The probability of this pathway is 1 − (1 − r _i )p ²/4 − p(1 − (1 − r _i )p/2) = 1 − p[1 − (1 − r _i )p/4].

$\underline{00 \rightarrow 00}$: The probability for this pathway is simply 1.

$$ 1 \leftrightarrow 4, 2 \leftrightarrow 3 $$

This case is symmetric to Case 2, so that all of the probabilities are identical.

Given a diploid parent and a diploid daughter cell, where the daughter is characterized by l ₁₀, l ₀₀, let $l_{i_1 i_2 j_1 j_2}$ denote the number of positions where the daughter is i ₁, i ₂ and the parent is j ₁, j ₂. The probability that the parent diploid produces the daughter diploid as the left daughter cell is then

$$ \begin{aligned} & p^{2 l_{1111}} [2 p (1 - p)]^{l_{1011}} (1 - p)^{2 l_{0011}} \left({\frac{r_i}{2}} p^2\right)^{l_{1110}} [p (1 - r_i p)]^{l_{1010}} [1 - p(1 - r_i p/2)]^{l_{0010}} \delta_{l_{1100} + l_{1000}, 0}, \\ & \hbox{for\;the}\;1 \leftrightarrow 2, 3 \leftrightarrow 4\; \hbox{mating\;pattern}.\\ & p^{2 l_{1111}} [2 p (1 - p)]^{l_{1011}} (1 - p)^{2 l_{0011}}\left({\frac{1 - r_i}{4}} p^2\right)^{l_{1110}} \left[p \left(1-{\frac{1 - r_i}{2}} p\right)\right]^{l_{1010}}\left[1 - p \left(1 - {\frac{1 - r_i}{4}} p\right)\right]^{l_{0010}} \delta_{l_{1100} + l_{1000}, 0}, \\ & \hbox{for\;the}\; 1 \leftrightarrow 3, 2 \leftrightarrow 4\;\hbox{and}\; 1 \leftrightarrow 4, 2 \leftrightarrow 3\; \hbox{mating\; patterns}. \end{aligned} $$

(67)

Taking into account degeneracies and the probabilities for the various mating patterns, we obtain

$$ \begin{aligned} & {\frac{d z_{l_{10}, l_{00}}}{dt}} = -(\kappa_{l_{00}} + \bar{\kappa}(t)) z_{l_{10}, l_{00}} + 2 {\frac{N!}{l_{10}! l_{00}! (N - l_{10} - l_{00})!}} \\ & \times \sum_{l_{1110} = 0}^{N - l_{10} - l_{00}} \sum_{l_{1100} = 0}^{N - l_{10} - l_{00} - l_{1110}} \sum_{l_{1010} = 0}^{l_{10}} \sum_{l_{1000} = 0}^{l_{10} - l_{1010}} \sum_{l_{0010} = 0}^{l_{00}} \sum_{l_{0000} = 0}^{l_{00} - l_{0010}} \kappa_{l_{1100} + l_{1000} + l_{0000}} {\frac{z_{l_{1110} + l_{1010} + l_{0010}, l_{1100} + l_{1000} + l_{0000}}} {{\left(\begin{array}{l}N\\ l_{1110} + l_{1010} + l_{0010}\\ \end{array}\right)} {\left(\begin{array}{l}N - l_{1110} - l_{1010}- l_{0010}\\ l_{1100} + l_{1000} + l_{0000}\\ \end{array}\right)}}} \\ & \times{\left(\begin{array}{l} N - l_{10} - l_{00}\\ l_{1110}\\ \end{array}\right)} {\left(\begin{array}{l} N - l_{10} - l_{00} - l_{1110}\\ l_{1100}\\ \end{array}\right)} {\left(\begin{array}{l} l_{10}\\ l_{1010}\\ \end{array}\right)} {\left(\begin{array}{l}l_{10} - l_{1010}\\ l_{1000}\\ \end{array}\right)}\times {\left(\begin{array}{l} l_{00}\\ l_{0010}\\ \end{array}\right)} {\left(\begin{array}{l} l_{00} - l_{0010}\\ l_{0000}\end{array}\right)} \\ & \times{\frac{1}{3}} [p^{2 l_{1111}} [2 p (1 - p)]^{l_{1011}} (1 - p)^{2 l_{0011}} \left({\frac{r_i}{2}} p^2\right)^{l_{1110}} [p (1 - r_i p)]^{l_{1010}} [1 - p(1 - r_i p/2)]^{l_{0010}} \delta_{l_{1100} + l_{1000}, 0}\\ & + 2 p^{2 l_{1111}} [2 p (1 - p)]^{l_{1011}} (1 - p)^{2 l_{0011}} \left({\frac{1 - r_i}{4}} p^2\right)^{l_{1110}} \left[p (1 - {\frac{1 - r_i}{2}} p)\right]^{l_{1010}} \left[1 - p (1 - {\frac{1 - r_i}{4}} p)\right]^{l_{0010}} & \times \delta_{l_{1100} + l_{1000}, 0}] \\ & = -(\kappa_{l_{00}} + \bar{\kappa}(t)) z_{l_{10}, l_{00}} + {\frac{2}{3}} \sum_{l_{1110} = 0}^{N - l_{10} - l_{00}} \sum_{l_{1010} = 0}^{l_{10}} \sum_{l_{0010} = 0}^{l_{00}} \sum_{l_{0000} = 0}^{l_{00} - l_{0010}} \kappa_{l_{0000}} z_{l_{1110} + l_{1010} + l_{0010}, l_{0000}} \\ & \times{\frac{(l_{1110} + l_{1010} + l_{0010})!}{l_{1110}! l_{1010}! l_{0010}!}} \\ &\times \left[\left[{\frac{r_i}{2}} (1 - \epsilon)^2\right]^{l_{1110}} [1 - \epsilon - r_i (1 - \epsilon)^2]^{l_{1010}} \left[\epsilon + {\frac{r_i}{2}} (1 - \epsilon)^2\right]^{l_{0010}} \right.\\ & \left.+ 2 \left[{\frac{1 - r_i}{4}} (1 - \epsilon)^2\right]^{l_{1110}} [1 - \epsilon - {\frac{1 - r_i}{2}} (1 - \epsilon)^2]^{l_{1010}} \left[\epsilon + {\frac{1 - r_i}{4}} (1 - \epsilon)^2\right]^{l_{0010}}\right] \\ &\times {\frac{(N - l_{1110} - l_{1010} - l_{0010} - l_{0000})!}{(l_{10} - l_{1010})! (l_{00} - l_{0010} - l_{0000})! (N - l_{10} - l_{00} - l_{1110})!}} \\ & \times[2 \epsilon (1 - \epsilon)]^{l_{10} - l_{1010}} \epsilon^{2 (l_{00} - l_{0010} - l_{0000})} (1 - \epsilon)^{2 (N - l_{10} - l_{00} - l_{1110})} \\ \end{aligned} $$

(68)

which is identical to Eq. (23).

Appendix C: Derivation of the evolutionary dynamics equations for sexual reproduction

Two-chromosomed genome

For sexual reproduction with random mating, the dynamical equations are:

$$ \begin{aligned} & {\frac{d n_{\{\sigma_1, \sigma_2\}}}{dt}} = -\kappa_{\{\sigma_1, \sigma_2\}} n_{\{\sigma_1, \sigma_2\}} + \left({\frac{\gamma}{V}}\right) n_{\sigma_1} n_{\sigma_2},\; \hbox{for}\; \sigma_1 \neq \sigma_2 \\ & {\frac{d n_{\{\sigma, \sigma\}}}{dt}} = -\kappa_{\{\sigma, \sigma\}} n_{\{\sigma, \sigma\}} + {\frac{1}{2}} \left({\frac{\gamma} {V}}\right) n_{\sigma}^2 \end{aligned} $$

(69)

$$ \begin{aligned} & {\frac{d n_{\sigma}}{dt}} = -\left({\frac{\gamma}{V}}\right) n_{\sigma} n_{H} + \sum_{\{\sigma_1, \sigma_2\}} \kappa_{\{\sigma_1, \sigma_2\}} n_{\{\sigma_1, \sigma_2\}} \\ & \times \sum_{\sigma_{11}} \sum_{\sigma_{12}} \sum_{\sigma_{21}} \sum_{\sigma_{22}} p(\sigma_1, \sigma_{11}) p(\sigma_1, \sigma_{12}) p(\sigma_2, \sigma_{21}) p(\sigma_2, \sigma_{22}) \\ & \times [\delta_{\sigma_{11}, \sigma} + \delta_{\sigma_{12}, \sigma} + \delta_{\sigma_{21}, \sigma} + \delta_{\sigma_{22}, \sigma}] \\ & = -\left({\frac{\gamma}{V}}\right) n_{\sigma} n_H + 2 \sum_{\{\sigma_1, \sigma_2\}} \kappa_{\{\sigma_1, \sigma_2\}} n_{\{\sigma_1, \sigma_2\}} [p(\sigma_1, \sigma) + p(\sigma_2, \sigma)] \\ & = -\left({\frac{\gamma}{V}}\right) n_{\sigma} n_H + 4 \sum_{\{\sigma_1, \sigma_2\}, \sigma_1 \neq \sigma_2} \kappa_{(\sigma_1, \sigma_2)} n_{(\sigma_1, \sigma_2)} [p(\sigma_1, \sigma) + p(\sigma_2, \sigma)]\\ & + 4 \sum_{\{\sigma^{\prime}, \sigma^{\prime}\}} \kappa_{(\sigma^{\prime}, \sigma^{\prime})} n_{(\sigma^{\prime}, \sigma^{\prime})} p(\sigma^{\prime}, \sigma) \\ & = -\left({\frac{\gamma}{V}}\right) n_{\sigma} n_H + 4 \sum_{(\sigma_1, \sigma_2)} \kappa_{(\sigma_1, \sigma_2)} n_{(\sigma_1, \sigma_2)} p(\sigma_1, \sigma) \end{aligned} $$

(70)

Defining the diploid ordered strand-pair population fractions via $x_{({\sigma_1,}\sigma_2)} =n_{({\sigma_1,}\sigma_2)}/n,$ and the haploid population fractions via x _σ = n _σ/(2n), we obtain, after converting from population numbers to population fractions, and using the fact that ρ = n/V, the dynamical equations,

$$ \begin{aligned} & {\frac{d x_{(\sigma_1, \sigma_2)}}{dt}} = -(\kappa_{(\sigma_1, \sigma_2)} + \bar{\kappa}(t)) x_{(\sigma_1, \sigma_2)} + 2 \gamma \rho x_{\sigma_1} x_{\sigma_2} \\ & {\frac{d x_{\sigma}}{dt}} = -\bar{\kappa}(t) x_{\sigma} - 2 \gamma \rho x_{\sigma} x_H + 2 \sum_{(\sigma_1, \sigma_2)} \kappa_{(\sigma_1, \sigma_2)} x_{(\sigma_1, \sigma_2)} p(\sigma_1, \sigma) \end{aligned} $$

(71)

In order to develop the evolutionary dynamics equations in terms of the $z_{l_{10}, l_{01}, l_{00}}$ and $z_{l_0} ,$ we proceed as follows: Given a haploid with genome σ, let l ₁ and l ₀ denote the number of positions where σ is 1 and 0, respectively. Given some (σ₁, σ₂), let $l_{i j_1 j_2}$ denote the number of positions where σ is i, σ₁ is j ₁, and σ₂ is j ₂. We then have

$$ p(\sigma_1, \sigma) = p^{l_{111} + l_{110}} (1 - p)^{l_{011} + l_{010}} \delta_{l_{101} + l_{100}, 0} $$

(72)

The evolutionary dynamics equations for the diploid population fractions $z_{l_{10}, l_{01}, l_{00}}$ are given by

$$ \begin{aligned} & {\frac{d z_{l_{10}, l_{01}, l_{00}}}{dt}} = -(\kappa_{l_{00}} + \bar{\kappa}(t)) z_{l_{10}, l_{01}, l_{00}} + 2 \gamma \rho {\frac{N!}{l_{10}! l_{01}! l_{00}! (N - l_{10} - l_{01} - l_{00})!}} {\frac{z_{l_{01} + l_{00}}}{{\left(\begin{array}{l}N\\ l_{01} + l_{00}\\ \end{array}\right)}}}\,{\frac{z_{l_{10} + l_{00}}}{{\left(\begin{array}{l} N\\ l_{10} + l_{00}\\ \end{array}\right)}}}\\ & = -(\kappa_{l_{00}} + \bar{\kappa}(t)) z_{l_{10}, l_{01}, l_{00}} + 2 \gamma \rho {\frac{(l_{10} + l_{00})! (l_{01} + l_{00})!} {l_{10}! l_{01}! l_{00}!}} \\ & \times{\frac{(N - l_{01} - l_{00})!}{(N - l_{10} - l_{01} - l_{00})!}}\,{\frac{(N - l_{10} - l_{00})!}{N!}} z_{l_{10} + l_{00}} z_{l_{01} + l_{00}} \\ & = -(\kappa_{l_{00}} + \bar{\kappa}(t)) z_{l_{10}, l_{01}, l_{00}} + 2 \gamma \rho {\frac{(l_{10} + l_{00})! (l_{01} + l_{00})!} {l_{10}! l_{01}! l_{00}!}} \\ & \times \left(\prod_{k = 1}^{l_{10}}{\frac{N - l_{10} - l_{01} - l_{00} + k} {N - l_{10} - l_{00} + k}}\right) \left(\prod_{k = 1}^{l_{00}}{\frac{1}{N - l_{00} + k}}\right) z_{l_{10} + l_{00}} z_{l_{01} + l_{00}} \end{aligned} $$

(73)

which is identical to the first equation in Eq. 28.

Taking into account the transition probabilities and various degeneracies, then for the haploids, we have

$$ \begin{aligned} \frac{d z_{l_0}}{dt} & = -\bar{\kappa}(t) z_{l_0} - 2 \gamma \rho z_{l_0} z_H + 2 \left(\begin{array}{l}N\\l_0\\\end{array}\right) \sum_{l_{110} = 0}^{N - l_0} \sum_{l_{101} = 0}^{N - l_0 - l_{110}} \sum_{l_{100} = 0}^{N - l_0 - l_{110} - l_{101}} \sum_{l_{010} = 0}^{l_0} \sum_{l_{001} = 0}^{l_0 - l_{010}} \sum_{l_{000} = 0}^{l_0 - l_{010} - l_{001}} \kappa_{l_{100} + l_{000}} \\ & \times{\frac{z_{l_{110} + l_{010}, l_{101} + l_{001}, l_{100} + l_{000}}}{{\left(\begin{array}{l}N\\ l_{110} + l_{010}\\ \end{array}\right)} {\left(\begin{array}{l} N - l_{110} - l_{010}\\ l_{101} + l_{001}\\ \end{array}\right)} {\left(\begin{array}{l}N - l_{110} - l_{010} - l_{101} - l_{001}\\ l_{100} + l_{000}\\ \end{array}\right)}}} \\ &\times {\left(\begin{array}{l}N - l_0 \\ l_{110}\\ \end{array}\right)} {\left(\begin{array}{l} N - l_0 - l_{110}\\ l_{101}\\ \end{array}\right)} {\left(\begin{array}{l}N - l_0 - l_{110} - l_{101}\\ l_{100}\\ \end{array}\right)} {\left(\begin{array}{l}l_0\\ l_{010}\end{array}\right)} {\left(\begin{array}{l}l_0 - l_{010}\\ l_{001}\end{array}\right)} {\left(\begin{array}{l}l_0 - l_{010} - l_{001}\\ l_{000}\end{array}\right)} \\ &\times p^{l_{111} + l_{110}} (1 - p)^{l_{011} + l_{010}} \delta_{l_{101} + l_{100}, 0} \\ & = -\bar{\kappa}(t) z_{l_0} - 2 \gamma \rho z_H z_{l_0} + 2 \sum_{l_{110} = 0}^{N - l_0} \sum_{l_{010} = 0}^{l_0} \sum_{l_{001} = 0}^{l_0 - l_{010}} \sum_{l_{000} = 0}^{l_0 - l_{010} - l_{001}} \kappa_{l_{000}} z_{l_{110} + l_{010}, l_{001}, l_{000}} \\ & \times{\frac{(l_{110} + l_{010})!}{l_{110}! l_{010}!}} (1 - \epsilon)^{l_{110}} \epsilon^{l_{010}} {\frac{(N - l_{110} - l_{010} - l_{001} - l_{000})!}{(l_0 - l_{010} - l_{001} - l_{000})! (N - l_0 - l_{110})!}} \epsilon^{l_0 - l_{010} - l_{001} - l_{000}} (1 - \epsilon)^{N - l_0 - l_{110}} \\ \end{aligned} $$

(74)

which is identical to the second equation in Eq. 28.

Multi-chromosomed genome

In order to derive the quasispecies equations for sexual replication with random mating for the multi-chromosome case, we proceed as follows: We assume that a diploid produces four haploids that may be lined up and labelled “1,” “2,” “3,” “4.” We wish to determine the probability that haploid “1” receives a certain genome from a given parent diploid. As with the asexual case, since each of the homologous pairs segregate independently of one another, we may consider the probabilities of the various segregation patterns for a given homologous pair. We consider each case in turn:

$\underline{ 11 {\rightarrow}1 }:$ If a given homologous pair in a parent diploid is 11, then the corresponding gene in the daughter haploid labeled “1” is the daughter of a 1 parent, so the probability that this daughter is itself a 1 is p. Therefore, the 11 → 1 probability is simply p.

$\underline{ 11 \rightarrow 0}$: Adopting a similar argument to the one given above, we obtain that the 11 → 0 probability is 1 − p.

$\underline{ 10 \rightarrow 1}$: If a given homologous pair in a parent diploid is 10, then since a 0 parent gene produces two 0 daughters, the corresponding gene in the daughter haploid labeled “1” can only be 1 if it is the daughter of the 1 parent. By the symmetry of the chromosome segregation, the probability that the haploid gene is the daughter of the 1 parent is 1/2. As the probability that a daughter of the 1 parent is itself a 1 is p, we obtain an overall probability of p/2.

$\underline{10 \rightarrow 0}$: As the probability of a 10 → 1 pathway is p/2 , the probability of the 10 → 0 pathway is 1 − p/2.

$\underline{00 \rightarrow 0}$: The probability of this pathway is 1.

Suppose a diploid is characterized by the parameters l ₁₀, l ₀₀. Suppose that two haploids, with sequences σ₁ and σ₂ fuse. If σ₁ ≠ σ₂, then the diploid production rate is given by (γ/V)$n_{\sigma_1}n_{\sigma_2},$ whereas if σ₁ = σ₂, then the diploid production rate is given by (1/2) (γ/V)$n_{\sigma_1}n_{\sigma_2}.$

If we let $\hat{\sigma} = (\{s_{11}, s_{12}\}, \ldots, \{s_{N1}, s_{N2}\})$ denote the genome of the diploid, where {s _i1, s _i2} = {1, 1}, {1, 0}, {0, 0}, and if we let $\hat{\sigma}^{\prime}$ denote the genome formed by the fusion of haploids with genomes σ₁ and σ₂, then we have

$$ \begin{aligned} \frac{d n_{\hat{\sigma}}}{dt} = & -\kappa_{\hat{\sigma}} n_{\hat{\sigma}} + \frac{\gamma}{V}\sum_{\{\sigma_1, \sigma_2\}, \sigma_1 \neq \sigma_2, \hat{\sigma}^{\prime} = \hat{\sigma}} n_{\sigma_1} n_{\sigma_2} + \frac{1}{2} \frac{\gamma}{V} \sum_{\{\sigma, \sigma\}, \hat{\sigma}^{\prime} = \hat{\sigma}} n_{\sigma}^2 \\ = & -\kappa_{\hat{\sigma}} n_{\hat{\sigma}} + \frac{1}{2} \frac{\gamma}{V}\sum_{(\sigma_1, \sigma_2), \hat{\sigma}^{\prime} = \hat{\sigma}} n_{\sigma_1} n_{\sigma_2} \end{aligned} $$

(75)

Now, where $\hat{\sigma}$ is {1, 1}, we must have that both σ₁ and σ₂ are 1, where $\hat{\sigma}$ is {0, 0}, we must have that both σ₁ and σ₂ are 0. Where $\hat{\sigma}$ is {1, 0}, we must have that σ₁ is 1 and σ₂ is 0, or σ₁ is 0 and σ₂ is 1. Let l denote the number of spots where σ₁ is 1 and σ₂ is 0. As we want the fusion of σ₁ and σ₂ to produce $\hat{\sigma} ,$ then the number of spots where σ₁ is 0 and σ₂ is 1 is l ₁₀ − l.

Taking into account degeneracies, and converting from population numbers to population fractions, we then have,

$$ \begin{aligned} \frac{d z_{l_{10}, l_{00}}}{dt} &= -(\kappa_{l_{00}} + \bar{\kappa}(t)) z_{l_{10}, l_{00}} + 2 \gamma \rho \frac{N!} {l_{10}! l_{00}! (N - l_{10} - l_{00})!} \sum_{l = 0}^{l_{10}} \left(\begin{array}{l} l_{10} \\ l\\ \end{array}\right) \frac{z_{l_{10} - l + l_{00}}} {\left(\begin{array}{l} N\\ l_{10} - l + l_{00} \end{array}\right)} \frac{z_{l + l_{00}}}{\left( \begin{array}{l} N \\ l + l_{00} \end{array}\right)}\\ & = -(\kappa_{l_{00}} + \bar{\kappa}(t)) z_{l_{10}, l_{00}} + 2 \gamma \rho \sum_{l = 0}^{l_{10}} \frac{(l + l_{00})! (l_{10} - l +l_{00})!}{l! (l_{10} - l)! l_{00}!}\\ & \times\left(\prod_{k =1}^{l}\frac{N - l_{10} - l_{00} + k}{N - l - l_{00} + k} \right) \left(\prod_{k = 1}^{l_{00}}\frac{1}{N - l_{00} + k}\right) z_{l + l_{00}}z_{l_{10}-l + l_{00}} \end{aligned} $$

(76)

which is identical to the first equation in Eq. 41.

In order to derive the haploid equations, suppose a haploid is characterized by the parameter l ₀. Given some parent diploid, let $l_{i j_1 j_2}$ denote the number of positions where the haploid is i and the diploid is j ₁, j ₂. We then have a total transition probability of

$$ p^{l_{111}} (1 - p)^{l_{011}}\left(\frac{p}{2}\right)^{l_{110}}\left(1 - \frac{p}{2}\right)^{l_{010}} \delta_{l_{100},0} $$

(77)

and so, taking into account degeneracies, we obtain

$$\begin{aligned} \frac{d z_{l_0}}{dt} &= -\bar{\kappa}(t) z_{l_0}- 2 \gamma \rho z_{l_0} z_H + 2\frac{N!}{l_0! (N - l_0)!}\sum_{l_{110} = 0}^{N - l_0}\sum_{l_{100} = 0}^{N - l_0 - l_{110}} \sum_{l_{010} = 0}^{l_0}\sum_{l_{000} = 0}^{l_0 - l_{010}}\kappa_{l_{100} + l_{000}}\frac{z_{l_{110} + l_{010}, l_{100} + l_{000}}}{ \left( \begin{array}{l} N\\ l_{110} + l_{010}\\ \end{array} \right) \left( \begin{array}{l} N - l_{110} - l_{010}\\ l_{100} + l_{000} \end{array} \right)}\\ &\times \left( \begin{array}{l} N - {l_{0}} \\ l_{110}\\ \end{array}\right) \left(\begin{array}{l} N - l_0 - l_{110}\\ l_{100}\\ \end{array} \right) \left(\begin{array}{l} l_0 \\ l_{010}\\ \end{array} \right) \left(\begin{array}{l} l_0 - l_{010}\\ l_{000}\\ \end{array} \right) p^{l_{111}}(1 - p)^{l_{011}} \left(\frac{p}{2}\right)^{l_{110}}\left(1 - \frac{p} {2}\right)^{l_{010}}\delta_{l_{100},0}\\ & = -\bar{\kappa}(t)z_{l_0} - 2 \gamma \rho z_H z_{l_0} + 2 \sum_{l_{110} = 0}^{N - l_0} \sum_{l_{010} = 0}^{l_0} \sum_{l_{000} = 0}^{l_0 - l_{010}} \kappa_{l_{000}} z_{l_{110} + l_{010}, l_{000}} \frac{(l_{110} + l_{010})!}{l_{110}! l_{010}!}\left(\frac{1 - \epsilon}{2}\right)^{l_{110}}\left(\frac{1 +\epsilon}{2}\right)^{l_{010}}\\ & \times \frac{(N - l_{110} - l_{010} - l_{000})!}{(l_0 - l_{010} - l_{000})! (N - l_0 - l_{110})!}\epsilon^{l_0 - l_{010} - l_{000}}(1 - \epsilon) ^{N - l_0 - l_{110}} \end{aligned} $$

(78)

which is identical to the second equation in Eq. 41.

Appendix D: Derivation of the dynamical equations for w _l (β₁, β₂, t) for asexual reproduction in the two-chromosomed genome

For asexual reproduction in the two-chromosomed genome, we have

$$ \begin{aligned} &\frac{\partial w_l}{\partial t} = -(\kappa_l + \bar{\kappa}(t))w_l + 2r_i \sum_{l_1 = 0}^{N - l} \sum_{l_2 = 0}^{N - l - l_1} \sum_{l_1^{\prime} = 0}^{N - l - l_1 - l_2} \sum_{l_2^{\prime} = 0}^{l_1} \sum_{l_3^{\prime} = 0}^{l_2} \sum_{l_4^{\prime} = 0}^{l} \sum_{l_5^{\prime} = 0}^{l - l_4^{\prime}} \sum_{l_6^{\prime} = 0}^{l - l_4^{\prime} - l_5^{\prime}} \kappa_{l_6^{\prime}} z_{l_1^{\prime} + l_2^{\prime} + l_3^{\prime} + l_4^{\prime}, l_5^{\prime}, l_6^{\prime}}\\ &\times \frac{(l_1^{\prime} + l_2^{\prime} + l_3^{\prime} + l_4^{\prime})!}{l_1^{\prime}! l_2^{\prime}! l_3^{\prime}! l_4^{\prime}!}[(1 - \epsilon)^2]^{l_1^{\prime}} [\beta_1 \epsilon (1 - \epsilon)]^{l_2^{\prime}} [\beta_2 \epsilon (1 - \epsilon)]^{l_3^{\prime}} (\epsilon^2)^{l_4^{\prime}}\\ &\times \frac{(N - l_1^{\prime} - l_2^{\prime} - l_3^{\prime} - l_4^{\prime} - l_5^{\prime} - l_6^{\prime})!}{(l_1 - l_2^{\prime})! (l_2 - l_3^{\prime})! (l - l_4^{\prime} - l_5^{\prime} - l_6^{\prime})! (N - l - l_1 - l_2 - l_1^{\prime})!}\\ &\times[\beta_1 \epsilon (1 - \epsilon)]^{l_1 - l_2^{\prime}} [\beta_2 \epsilon (1 - \epsilon)]^{l_2 - l_3^{\prime}} (\epsilon^2)^{l - l_4^{\prime} - l_5^{\prime} - l_6^{\prime}} [(1 - \epsilon)^2]^{N - l - l_1 - l_2 - l_1^{\prime}} \\ & + 2 (1 - r_i) \sum_{l_1 = 0}^{N - l} \sum_{l_2 = 0}^{N - l - l_1} \sum_{l_1^{\prime} = 0}^{l_1} \sum_{l_2^{\prime} = 0}^{l_2} \sum_{l_3^{\prime} = 0}^{l} \sum_{l_4^{\prime} = 0}^{l - l_3^{\prime}} \sum_{l_5^{\prime} = 0}^{l - l_3^{\prime} - l_4^{\prime}} \kappa_{l_5^{\prime}} z_{l_1^{\prime} + l_3^{\prime}, l_2^{\prime} + l_4^{\prime}, l_5^{\prime}} \\ &\times \frac{(l_1^{\prime} + l_3^{\prime})!}{l_1^{\prime}! l_3^{\prime}!}[\beta_1 (1 - \epsilon)]^{l_1^{\prime}} \epsilon^{l_3^{\prime}} \frac{(l_2^{\prime} + l_4^{\prime})!}{l_2^{\prime}! l_4^{\prime}!} [\beta_2 (1 - \epsilon)]^{l_2^{\prime}} \epsilon^{l_4^{\prime}}\\ &\times \frac{(N - l_1^{\prime} - l_2^{\prime} - l_3^{\prime} - l_4^{\prime} - l_5^{\prime})!}{(l_1 - l_1^{\prime})! (l_2 - l_2^{\prime})! (l - l_3^{\prime} - l_4^{\prime} - l_5^{\prime})! (N - l - l_1 - l_2)!}\\ &\times [\beta_1 \epsilon (1 - \epsilon)]^{l_1 - l_1^{\prime}} [\beta_2 \epsilon (1 - \epsilon)]^{l_2 - l_2^{\prime}} (\epsilon^2)^{l - l_3^{\prime} - l_4^{\prime} - l_5^{\prime}} [(1 - \epsilon)^2]^{N - l - l_1 - l_2}\\ & = -(\kappa_l + \bar{\kappa}(t)) w_l \\ & + 2 r_i \sum_{l_6^{\prime} = 0}^{l} \sum_{l_5^{\prime} = 0}^{l - l_6^{\prime}} \sum_{l_4^{\prime} = 0}^{l - l_5^{\prime} - l_6^{\prime}} \sum_{l_1^{\prime} = 0}^{N - l} \sum_{l_2^{\prime} = 0}^{N - l - l_1^{\prime}} \sum_{l_3^{\prime} = 0}^{N - l - l_1^{\prime} - l_2^{\prime}} \sum_{l_1 - l_2^{\prime} = 0}^{N - l - l_1^{\prime} - l_2^{\prime} - l_3^{\prime}}\sum_{l_2 - l_3^{\prime} = 0}^{N - l - l_1^{\prime} - l_2^{\prime} - l_3^{\prime} - (l_1 - l_2^{\prime})} \kappa_{l_6^{\prime}} z_{l_1^{\prime} + l_2^{\prime} + l_3^{\prime} + l_4^{\prime}, l_5^{\prime}, l_6^{\prime}}\\ &\times \frac{(l_1^{\prime} + l_2^{\prime} + l_3^{\prime} + l_4^{\prime})!}{l_1^{\prime}! l_2^{\prime}! l_3^{\prime}! l_4^{\prime}!} [(1 - \epsilon)^2]^{l_1^{\prime}} [\beta_1 \epsilon (1 - \epsilon)]^{l_2^{\prime}} [\beta_2 \epsilon (1 - \epsilon)]^{l_3^{\prime}} (\epsilon^2)^{l_4^{\prime}} \\ &\times \frac{(N - l_1^{\prime} - l_2^{\prime} - l_3^{\prime} - l_4^{\prime} - l_5^{\prime} - l_6^{\prime})!}{(l_1 - l_2^{\prime})! (l_2 - l_3^{\prime})! (l - l_4^{\prime} - l_5^{\prime} - l_6^{\prime})! (N - l - l_1 - l_2 - l_1^{\prime})!}\\ &\times [\beta_1 \epsilon (1 - \epsilon)]^{l_1 - l_2^{\prime}} [\beta_2 \epsilon (1 - \epsilon)]^{l_2 - l_3^{\prime}} (\epsilon^2)^{l - l_4^{\prime} - l_5^{\prime} - l_6^{\prime}} [(1 - \epsilon)^2]^{N - l - l_1 - l_2 - l_1^{\prime}} \\ &+ 2 (1 - r_i)\sum_{l_5^{\prime} = 0}^{l} \sum_{l_4^{\prime} = 0}^{l - l_5^{\prime}} \sum_{l_3^{\prime} = 0}^{l - l_4^{\prime} - l_5^{\prime}} \sum_{l_1^{\prime} = 0}^{N - l} \sum_{l_2^{\prime} = 0}^{N - l - l_1^{\prime}} \sum_{l_1 - l_1^{\prime} = 0}^{N - l - l_1^{\prime} - l_2^{\prime}} \sum_{l_2 - l_2^{\prime} = 0}^{N - l - l_1^{\prime} - l_2^{\prime} - (l_1 - l_1^{\prime})} \kappa_{l_5^{\prime}} z_{l_1^{\prime} + l_3^{\prime}, l_2^{\prime} + l_4^{\prime}, l_5^{\prime}} \\ &\times \frac{(l_1^{\prime} + l_3^{\prime})!}{l_1^{\prime}! l_3^{\prime}!}[\beta_1 (1 - \epsilon)]^{l_1^{\prime}} \epsilon^{l_3^{\prime}} \frac{(l_2^{\prime} + l_4^{\prime})!} {l_2^{\prime}! l_4^{\prime}!} [\beta_2 (1 -\epsilon)]^{l_2^{\prime}} \epsilon^{l_4^{\prime}}\\ & \times \frac{(N - l_1^{\prime} - l_2^{\prime} - l_3^{\prime} - l_4^{\prime} - l_5^{\prime})!}{(l_1 - l_1^{\prime})! (l_2 - l_2^{\prime})! (l - l_3^{\prime} - l_4^{\prime} - l_5^{\prime})! (N - l - l_1 - l_2)!}\\ & \times [\beta_1 \epsilon (1 - \epsilon)]^{l_1 - l_1^{\prime}} [\beta_2 \epsilon (1 - \epsilon)]^{l_2 - l_2^{\prime}} (\epsilon^2)^{l - l_3^{\prime} - l_4^{\prime} - l_5^{\prime}} [(1 - \epsilon)^2]^{N - l - l_1 - l_2}\\ & \geq -(\kappa_l + \bar{\kappa}(t)) w_l + 2 r_i \kappa_l \sum_{l_1^{\prime} = 0}^{N - l} \sum_{l_2^{\prime} = 0}^{N - l - l_1^{\prime}} \sum_{l_3^{\prime} = 0}^{N - l - l_1^{\prime} - l_2^{\prime}} \sum_{l_1 - l_2^{\prime} = 0}^{N - l - l_1^{\prime} - l_2^{\prime} - l_3^{\prime}} \sum_{l_2 - l_3^{\prime} = 0}^{N - l - l_1^{\prime} - l_2^{\prime} - l_3^{\prime} - (l_1 - l_2^{\prime})} z_{l_1^{\prime} + l_2^{\prime} + l_3^{\prime}, 0, l} \\ &\times \frac{(l_1^{\prime} + l_2^{\prime} + l_3^{\prime})!}{l_1^{\prime}! l_2^{\prime}! l_3^{\prime}!}[(1 - \epsilon)^2]^{l_1^{\prime}} [\beta_1 \epsilon (1 - \epsilon)]^{l_2^{\prime}} [\beta_2 \epsilon (1 - \epsilon)]^{l_3^{\prime}} \\ &\times \frac{(N - l - l_1^{\prime} - l_2^{\prime} - l_3^{\prime})!}{(l_1 - l_2^{\prime})! (l_2 - l_3^{\prime})! (N - l - l_1 - l_2 - l_1^{\prime})!} [\beta_1 \epsilon (1 - \epsilon)]^{l_1 - l_2^{\prime}} [\beta_2 \epsilon (1 - \epsilon)]^{l_2 - l_3^{\prime}} [(1 - \epsilon)^2]^{N - l - l_1 - l_2 - l_1^{\prime}} \\ & + 2 (1 - r_i) \kappa_l \sum_{l_1^{\prime} = 0}^{N - l} \sum_{l_2^{\prime} = 0}^{N - l - l_1^{\prime}} \sum_{l_1 - l_1^{\prime} = 0}^{N - l - l_1^{\prime} - l_2^{\prime}} \sum_{l_2 - l_2^{\prime} = 0}^{N - l - l_1^{\prime} - l_2^{\prime} - (l_1 - l_1^{\prime})} z_{l_1^{\prime}, l_2^{\prime}, l} [\beta_1 (1 - \epsilon)]^{l_1^{\prime}} [\beta_2 (1 - \epsilon)]^{l_2^{\prime}}\\ &\times \frac{(N - l - l_1^{\prime} - l_2^{\prime})!}{(l_1 - l_1^{\prime})! (l_2 - l_2^{\prime})! (N - l - l_1 - l_2)!}[\beta_1 \epsilon (1 - \epsilon)]^{l_1 - l_1^{\prime}} [\beta_2 \epsilon (1 - \epsilon)]^{l_2 - l_2^{\prime}} [(1 - \epsilon)^2]^{N - l - l_1 - l_2}\\ & = \kappa_l \left[2 ((\beta_1 + \beta_2) \epsilon (1 - \epsilon) + (1 - \epsilon)^2)^{N - l} \right.\\ & \left.\times \left(r_i w_l(1, 0, t) + (1 - r_i) w_l\left(\frac{\beta_1 (1 - \epsilon)}{(\beta_1 + \beta_2) \epsilon (1 - \epsilon) + (1 - \epsilon)^2}, \frac{\beta_2 (1 - \epsilon)}{(\beta_1 + \beta_2) \epsilon (1 - \epsilon) + (1 - \epsilon)^2}, t\right)\right) - w_l(\beta_1, \beta_2, t)\right] \\ & - \bar{\kappa}(t) w_l(\beta_1, \beta_2, t) \end{aligned} $$

(79)

where strict equality holds for l = 0, or if $z_{l_1, l_2, l_3} =0$ for l ₃ < l.

Appendix E: Mathematical details for the solution of the sexual reproduction pathways in the limit of large N

Two-chromosomed genome

We begin our analysis by deriving the limiting form of the expression:

$$ \frac{(l_1 + l_3)! (l_2 + l_3)!}{l_1! l_2! l_3!} \prod_{k = 1}^{l_1} \frac{N - l_1 - l_2 - l_3 + k}{N - l_1 - l_3 + k} \prod_{k = 1}^{l_3} \frac{1}{N - l_3 + k} $$

(80)

in the limit of large N, under the assumption that l ₁, l ₂ scale as $\sqrt{N},$ and l ₃ is finite as N → ∞.

We begin by re-writing the expression as

$$ \frac{1}{l_3!} \prod_{k = 1}^{l_3} \frac{(l_1 + k) (l_2 + k)} {N - l_3 + k}\prod_{k = 1}^{l_1} \frac{1 + \frac{k - l_1 - l_2 - l_3} {N}}{1 - \frac{l_1 + l_3 - k}{N}} $$

(81)

In the limit of large N, we obtain

$$ \begin{aligned} &\frac{1}{l_3!} \prod_{k = 1}^{l_3}\frac{\left(\frac{l_1}{\sqrt{N}} + \frac{k}{\sqrt{N}}\right) \left(\frac{l_2}{\sqrt{N}} + \frac{k} {\sqrt{N}}\right)}{1 + \frac{k - l_3}{N}}\prod_{k = 1}^{l_1} \left(1 + \frac{k - l_1 - l_2 - l_3}{N}\right)\left(1 + \frac{l_1 + l_3 - k}{N}\right) \\ & \rightarrow \frac{1}{l_3!}\left(\frac{l_1 l_2}{N}\right)^{l_3} \left(1 - \frac{l_2}{N}\right)^{l_1} \rightarrow \frac{1}{l_3!} \left(\frac{l_1 l_2}{N}\right)^{l_3} \left[\left(1 - \frac{l_2} {N}\right)^{-\,\frac{N}{l_2}}\right]^{-\frac{l_1 l_2}{N}} \rightarrow \frac{1}{l_3!}\left(\frac{l_1 l_2}{N}\right)^{l_3} e^{-\,\frac{l_1 l_2} {N}} \end{aligned} $$

(82)

Also, as is given in Eq. 35, we have

$$ \tilde{z}_l = 2 e^{-\mu} \sum_{k = 0}^{l} \frac{\mu^{k}}{k!} \tilde{z}_{l - k} \sum_{l_4 = 0}^{l - k} \frac{\kappa_{l_4}} {\bar{\kappa} + \kappa_{l_4}}\sum_{l_1 = 0}^{N - l} \frac{1} {l_4!}\left(\frac{l_1 (l - l_4 - k)}{N}\right)^{l_4} e^{-\,\frac{l_1 (l - l_4 - k)}{N}}\tilde{z}_{l_1 + l_4} $$

(83)

Now, in the limit of large N, we have observed from simulations that the $\tilde{z}_l$ converge to a Gaussian distribution with a mean that is proportional to $\sqrt{N}$ and a standard deviation that is proportional to N ^1/4. While this observation is not a proof, we may nevertheless make an ansatz that the $\tilde{z}_l$ do indeed converge to a Gaussian in the limit of large N, and see if this allows us to solve for the steady state of this reproduction pathway. If this ansatz leads to a self-consistent set of equations that may be used to solve for the steady state in the limit of large N, then we may assume that it is a correct assumption.

If the mean of the Gaussian scales as $\sqrt{N},$ then we may write that the mean of the Gaussian is given by ${\lambda}\sqrt{N}.$ If the standard deviation of the Gaussian scales as N ^1/4, then we may write that the standard deviation is γN ^1/4. As a result, we may transform from a discrete representation in terms of the $\tilde{z}_l$ into a continuous representation, denoted by p(x), where $x =l/\sqrt{N}.$ Conservation of probability implies that $\tilde{z}_l = p(x)/\sqrt{N} \Rightarrow p(x) = \sqrt{N} \tilde{z}_l .$

In these re-scaled coordinates, the Gaussian has a mean of λ and a standard deviation of γN ^−1/4. As a result, we obtain that

$$ p(x) = \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} e^{-\,\frac{\sqrt{N}(x - \lambda)^2}{2 \gamma^2}} $$

(84)

We then have

$$ \begin{aligned} & p(x) = 2 e^{-\mu}\sum_{l_4 = 0}^{x \sqrt{N}}\frac{1}{l_4!} \frac{\kappa_{l_4}}{\bar{\kappa} + \kappa_{l_4}}\sum_{k = 0}^{x \sqrt{N} - l_4}\frac{\mu^{k}}{k!} p\left(x - \frac{k}{\sqrt{N}}\right)\\ &\times \sum_{l_1 = 0}^{N - x \sqrt{N}}\frac{1}{\sqrt{N}} \left(\frac{l_1}{\sqrt{N}} \left(x - \frac{l_4 + k} {\sqrt{N}}\right)\right)^{l_4} e^{-\,\frac{l_1}{\sqrt{N}}\left(x - \frac{l_4 + k}{\sqrt{N}}\right)} p\left(\frac{l_1}{\sqrt{N}} + \frac{l_4}{\sqrt{N}}\right) \end{aligned} $$

(85)

Defining $x_1 =l_1/\sqrt{N}$ we have, in the limit of large N, that

$$ \begin{aligned} & p(x) = 2 e^{-\mu} \sum_{l_4 = 0}^{\infty} \frac{1}{l_4!} \frac{\kappa_{l_4}}{\bar{\kappa} + \kappa_{l_4}}\sum_{k = 0}^{\infty} \frac{\mu^{k}}{k!} p\left(x - \frac{k}{\sqrt{N}}\right)\\ &\times \int\limits_{0}^{\infty} d x_1 (x_1 x)^{l_4} \left(1 - \frac{l_4 + k} {\sqrt{N} x}\right)^{l_4} e^{-x_1 x} e^{x_1 \frac{l_4 + k}{\sqrt{N}}} p\left(x_1 + \frac{l_4}{\sqrt{N}}\right) \end{aligned} $$

(86)

In the limit of large N, we can evaluate the integral out to order $1/\sqrt{N}.$ The idea is that the integrand is a product of two functions of x ₁, where one of the functions is a Gaussian that converges to a δ-function centered at λ. The integral is then evaluated to order $1/\sqrt{N}$ by expanding the other function out to second order in x ₁ − λ, and integrating under the narrow Gaussian envelope. In the Taylor expansion, we may ignore any terms containing an $x_1^n/\sqrt{N}$ where n ≥ 1, since such terms either vanish or contribute a term of order at least 1/N.

According to these guidelines, the integral becomes

$$\begin{aligned}& \lambda^{l_4}\left(1 + \lambda\frac{l_4 + k}{\sqrt{N}}\right) x^{l_4} \left(1 -\frac{l_4 (l_4 + k)}{\sqrt{N} x}\right) e^{-\lambda x} \int\limits_{0}^{\infty} dx_1 \left[1 + l_4\frac{x_1 - \lambda}{\lambda} + \frac{l_{4} (l_{4} - 1)}{2} \left(\frac{x_1 -\lambda}{\lambda}\right)^2\right]\\ & \times \left[1 - x (x_1 - \lambda) + \frac{1}{2} x^2(x_1 - \lambda)^2\right]\frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2}\left(x_1 - \lambda + \frac{l_4}{\sqrt{N}}\right)^2\right]\end{aligned}$$

(87)

Defining x′₁ = x ₁ − λ, this becomes

$$ \begin{aligned} \,&\lambda^{l_4} \left(1 + \lambda \frac{l_4 + k}{\sqrt{N}}\right) x^{l_4} \left(1 - \frac{l_4 (l_4 + k)}{\sqrt{N} x}\right) e^{-\lambda x} \int\limits_{-\infty}^{\infty} d x_1^{\prime} \left[1 + \frac{l_4}{\lambda} x_1^{\prime} + \frac{l_4 (l_4 - 1)}{2 \lambda^2} x_1^{\prime 2}\right]\\ &\quad\times \left[1 - x x_1^{\prime} + \frac{1}{2} x^2 x_1^{\prime 2}\right] \hbox{exp} \left[-x_{1}^{\prime} \frac{l_{4}}{\gamma^2}\right] \hbox{exp}\left[-\frac{l_4^2}{2 \sqrt{N} \gamma^2}\right]\frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} x_1^{\prime 2}\right] \\ &\quad = \lambda^{l_4}\left(1 + \lambda \frac{l_4 + k}{\sqrt{N}}\right) \left(1 - \frac{l_4^2}{2 \sqrt{N} \gamma^2}\right) x^{l_4} \left(1 - \frac{l_4 \left(l_4 + k\right)}{\sqrt{N} x}\right) e^{-\lambda x} \\ &\quad\times \int\limits_{-\infty}^{\infty} d x_1^{\prime} \left[1 + \left(\frac{l_4}{\lambda} - x\right) x_1^{\prime} + \left(\frac{1}{2} x^2 - \frac{l_4}{\lambda} x + \frac{l_4 \left(l_4 - 1\right)}{2 \lambda^2}\right) x_1^{\prime 2}\right] \\ &\quad\times \left[1 - \frac{l_4}{\gamma^2} x_1^{\prime} + \frac{l_4^2}{2 \gamma^4} x_1^{\prime 2}\right] \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} x_1^{\prime 2}\right]\\ &\quad = \lambda^{l_4} \left[1 + \frac{1}{\sqrt{N}} \left(\lambda (l_4 + k) - \frac{l_4^2}{2 \gamma^2} - \frac{l_4 (l_4 + k)}{x}\right)\right] x^{l_4} e^{-\lambda x}\\ &\quad\times \int\limits_{-\infty}^{\infty} d x_1^{\prime} \left[1 + \left(\frac{l_4^2} {2 \gamma^4} - \frac{l_4}{\gamma^2}\left(\frac{l_4} {\lambda} - x\right) + \frac{1}{2} x^2 - \frac{l_4}{\lambda} x + \frac{l_4(l_4 - 1)}{2 \lambda^2}\right) x_1^{\prime 2}\right] \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} x_1^{\prime 2}\right] \\ &\quad = \lambda^{l_4} x^{l_4} e^{-\lambda x} \left[1 + \frac{1}{\sqrt{N}} \left(\lambda(l_4 + k) - \frac{l_4 (l_4 + k)}{x} - l_4 \left(\frac{l_4} {\lambda} - x\right) + \frac{1}{2} \gamma^2 x^2 - \frac{l_4 \gamma^2} {\lambda} x + \frac{l_4 (l_4 - 1) \gamma^2}{2 \lambda^2}\right)\right] \end{aligned} $$

(88)

Now, instead of working with p(x) directly, we work with its Laplace Transform, P(s) ≡ ∫ ^∞₀ p(x)e ^−sx d x. By Taylor expanding out to second order in x − λ, we have that, to first order in $1/\sqrt{N},$ the Laplace Transform of p(x) is given by

$$ \begin{aligned} P(s) &= e^{-s \lambda} \int\limits_{0}^{\infty} d x \left(1 - s (x - \lambda) + \frac{1}{2} s^2 (x - \lambda)^2\right) \frac{N^{1/4}}{\gamma \sqrt{2 \pi}}\hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} (x - \lambda)^2\right]\\ & = e^{-s \lambda} \int\limits_{-\infty}^{\infty} \left[1 - s x^{\prime} + \frac{1}{2} s^2 x^{\prime 2}\right] \frac{N^{1/4}}{\gamma \sqrt{2 \pi}}\hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} x^{\prime 2}\right] \\ & = e^{-s \lambda} \left(1 + \frac{\gamma^2}{2 \sqrt{N}}s^2\right) \end{aligned} $$

(89)

We also have

$$ \begin{aligned} & P(s) = 2 e^{-\mu} \sum_{l_4 = 0}^{\infty} \frac{1}{l_4!} \frac{\lambda^{l_4}\kappa_{l_4}}{\bar{\kappa} + \kappa_{l_4}} \sum_{k = 0}^{\infty} \frac{\mu^{k}}{k!}\int\limits_{0}^{\infty} d x e^{-s x} x^{l_4} e^{-\lambda x}\\ &\times \left[1 + \frac{1}{\sqrt{N}} \left(\lambda (l_4 + k) - \frac{l_4 (l_4 + k)}{x} - l_4 \left(\frac{l_4}{\lambda} - x\right) + \frac{1}{2} \gamma^2 x^2 - \frac{l_4 \gamma^2}{\lambda}x +\frac{l_4 (l_4 - 1) \gamma^2}{2 \lambda^2}\right)\right]\\ &\times \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} \left(x - \lambda - \frac{k} {\sqrt{N}}\right)^2\right]\\ & = 2 e^{-\mu} e^{-s \lambda} e^{-\lambda^2} \sum_{l_4 = 0}^{\infty} \frac{1}{l_{4}!}\frac{\lambda^{2 l_4}\kappa_{l_4}}{\bar{\kappa} + \kappa_{l_4}}\sum_{k = 0}^{\infty} \frac{\mu^{k}}{k!}\\ &\times \int\limits_{-\infty}^{\infty} d x^{\prime}\left(1 - s x^{\prime} + \frac{1}{2} s^2 x^{\prime 2}\right)\left(1 + \frac{l_4}{\lambda} x^{\prime} + \frac{l_4(l_4-1)}{2 \lambda^2} x^{\prime 2}\right) \left(1 - \lambda x^{\prime} + \frac{1}{2} \lambda^2 x^{\prime 2}\right) \\ &\times \left[1 + \frac{1}{\sqrt{N}}\left(\lambda (l_4 + k) - \frac{l_4 (l_4 + k)}{\lambda} - l_4 \left(\frac{l_4}{\lambda} - \lambda\right) + \frac{1}{2}\gamma^2 \lambda^2 - l_4 \gamma^2 + \frac{l_4 (l_4 - 1) \gamma^2}{2 \lambda^2}\right)\right]\\ &\times \hbox{exp}\left[-\frac{k^2}{2 \sqrt{N} \gamma^2}\right] \hbox{exp}\left[\frac{k x^{\prime}}{\gamma^2}\right] \frac{N^{1/4}}{\gamma \sqrt{2 \pi}}\hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} x^{\prime 2}\right]\\ & = 2 e^{-\mu} e^{-s \lambda} e^{-\lambda^2} \sum_{l_4 = 0}^{\infty} \frac{1}{l_4!}\frac{\lambda^{2 l_4} \kappa_{l_4}} {\bar{\kappa} + \kappa_{l_4}}\sum_{k = 0}^{\infty} \frac{\mu^{k}}{k!}\\ &\times \left[1 + \frac{1}{\sqrt{N}} \left(\lambda(l_4 + k) - \frac{l_4 (l_4 + k)}{\lambda} - l_4\left(\frac{l_4}{\lambda} - \lambda\right) + \frac{1}{2} \gamma^2 \lambda^2 - l_4 \gamma^2 + \frac{l_4 (l_4 - 1) \gamma^2}{2 \lambda^2} - \frac{k^2}{2\gamma^2}\right)\right]\\ &\times \int\limits_{-\infty}^{\infty} d x^{\prime} \left[1 + \left(\frac{l_4}{\lambda} - s\right) x^{\prime} + \left(\frac{1}{2} s^2 - \frac{l_4 s}{\lambda} + \frac{l_4 (l_4 - 1)}{2 \lambda^2}\right) x^{\prime 2}\right]\\ &\times \left[1 + \left(\frac{k}{\gamma^2} - \lambda\right) x^{\prime} + \left(\frac{1}{2} \lambda^2 - \frac{k \lambda}{\gamma^2} + \frac{k^2}{2 \gamma^4}\right) x^{\prime 2}\right] \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2\gamma^2} x^{\prime 2}\right]\\ & = 2 e^{-\mu} e^{-s \lambda} e^{-\lambda^2} \sum_{l_4 = 0}^{\infty} \frac{1}{l_4!}\frac{\lambda^{2 l_4} \kappa_{l_4}}{\bar{\kappa} + \kappa_{l_4}}\sum_{k = 0}^{\infty} \frac{\mu^{k}}{k!}\\ &\times \left[1 + \frac{1}{\sqrt{N}}\left(\lambda (l_4 + k) - \frac{l_4 (l_4 + k)}{\lambda} - l_4\left(\frac{l_4}{\lambda} - \lambda\right) +\frac{1}{2} \gamma^2 \lambda^2 - l_4 \gamma^2 + \frac{l_4 (l_4 - 1) \gamma^2}{2 \lambda^2} - \frac{k^2}{2 \gamma^2}\right)\right]\\ &\times \int\limits_{-\infty}^{\infty} d x^{\prime} \left[1 + \left(\frac{1}{2} s^2 - \frac{l_4 s}{\lambda} + \frac{l_4 (l_4 - 1)}{2 \lambda^2} + \left(\frac{l_4}{\lambda} - s\right) \left(\frac{k} {\gamma^2} - \lambda\right) + \frac{1}{2} \lambda^2 - \frac{k\lambda}{\gamma^2} + \frac{k^2}{2 \gamma^4}\right) x^{\prime 2}\right] \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} x^{\prime 2}\right]\\ & = 2 e^{-\mu} e^{-s \lambda} e^{-\lambda^2} \sum_{l_4 = 0}^{\infty} \frac{1}{l_4!} \frac{\lambda^{2 l_4} \kappa_{l_4}}{\bar{\kappa} + \kappa_{l_4}} \sum_{k = 0}^{\infty} \frac{\mu^{k}}{k!}\\ &\times \left[1 + \frac{1}{\sqrt{N}}\left(\left(\lambda - \frac{l_4}{\lambda}\right) (2 l_4 + k) + \gamma^2 (\lambda^2 - l_4) + \frac{l_4 (l_4 - 1) \gamma^2}{\lambda^2} + \frac{l_4}{\lambda} (k - \lambda \gamma^2) - k \lambda \right.\right.\\ &\left.\left. + \left(\lambda \gamma^2 - k - \frac{l_4 \gamma^2}{\lambda}\right) s + \frac{1}{2} \gamma^2 s^2\right)\right] \\ & = 2 e^{-s \lambda} e^{-\lambda^2} \sum_{l_4 = 0}^{\infty} \frac{1} {l_4!} \frac{\lambda^{2 l_4} \kappa_{l_4}}{\bar{\kappa} + \kappa_{l_4}}\\ &\times \left[1 + \frac{1}{\sqrt{N}} \left(\left(\lambda - \frac{l_4}{\lambda}\right) (2 l_4 + \mu) + \gamma^2 (\lambda^2 - l_4) + \frac{l_4 (l_4 - 1) \gamma^2}{\lambda^2} + \frac{l_4}{\lambda} (\mu - \lambda \gamma^2) - \lambda \mu \right.\right.\\ & + \left.\left.\left(\lambda \gamma^2 - \mu - \frac{l_4 \gamma^2} {\lambda}\right)s + \frac{1}{2} \gamma^2 s^2\right)\right] \end{aligned} $$

(90)

Matching powers of s between the two expressions for P(s) gives:

$$ \begin{aligned} 1 &= 2 e^{-\lambda^2} \sum_{l_4 = 0}^{\infty} \frac{1}{l_4!} \frac{\lambda^{2 l_4} \kappa_{l_4}}{\bar{\kappa} + \kappa_{l_4}} \left[1 + \frac{1}{\sqrt{N}} \left((\lambda - \frac{l_4}{\lambda})(2 l_4 + \mu) + \gamma^2 (\lambda^2 - l_4) \right.\right.\\ & \left.\left.+ \frac{l_4 (l_4 - 1) \gamma^2}{\lambda^2} + \frac{l_4}{\lambda} (\mu - \lambda \gamma^2) - \lambda \mu\right)\right] \\ 0 &= 2 e^{-\lambda^2} \sum_{l_4 = 0}^{\infty} \frac{1}{l_4!} \frac{\lambda^{2 l_4} \kappa_{l_4}}{\bar{\kappa} + \kappa_{l_4}} \left[\lambda \gamma^2 - \mu - \frac{l_4 \gamma^2}{\lambda}\right]\\ 1 &= 2 e^{-\lambda^2} \sum_{l_4 = 0}^{\infty} \frac{1}{l_4!} \frac{\lambda^{2 l_4} \kappa_{l_4}}{\bar{\kappa} + \kappa_{l_4}} \end{aligned} $$

(91)

As N → ∞, the $1/\sqrt{N}$ term in the first equality becomes negligible, and so the first and the third equalities become identical to one another. As a result, we obtain the pair of equations:

$$ \begin{aligned} 1 &= 2 e^{-\lambda^2} \sum_{l_4 = 0}^{\infty} \frac{1}{l_4!} \frac{\lambda^{2 l_4} \kappa_{l_4}}{\bar{\kappa} + \kappa_{l_4}}\\ \mu &= \lambda \gamma^2 \left(1 - 2 e^{-\lambda^2} \sum_{l_4 = 0}^{\infty} \frac{1}{l_4!} \frac{\lambda^{2 l_4} \kappa_{l_4 + 1}}{\bar{\kappa} + \kappa_{l_4 + 1}}\right) \end{aligned} $$

(92)

Note that these equations are not sufficient by themselves to solve for $\bar{\kappa}, {\lambda,}{\gamma}.$ However, they show that the assumption of a Gaussian profile leads to a self-consistent set of equations that allows us to solve for the steady state of the system in the limit of large N. This validates the analysis carried out in the main text, which leads us to the large N result of $\bar{\kappa} = \hbox{max}\{2 e^{-\mu} - 1, 0\} .$

Multi-chromosomed genome

We may transform Eq. (47) into its continuous analogue as follows. We first note that the binomial probability distribution $2^{-N}\left(\begin{array}{l}N\\ n\\ \end{array}\right)$ approaches a Gaussian in the limit of large N, with a mean of N/2 and a variance σ² = N/4. As a normalized Gaussian is given by

$$ \frac{1}{\sigma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{(x-\bar{x})^2}{2 \sigma^2}\right] $$

(93)

we obtain, in the limit of large N, that

$$ 2^{-N} \left(\begin{array}{l}N\\n\\\end{array}\right) \rightarrow \sqrt{\frac{2}{\pi N}} \hbox{exp}\left[-2 \frac{\left(n - \frac{N}{2}\right)^2}{N}\right] $$

(94)

Therefore, we have that

$$ \begin{aligned} &\tilde{z}_l = 2 e^{-\mu} \sum_{l_3 = 0}^{l} \frac{1}{l_3!} \frac{\kappa_{l_3}}{\bar{\kappa} + \kappa_{l_3}} \sum_{k = 0}^{l - l_3} \frac{\mu^{k}}{k!} \sum_{l_{1} = 0}^{N - l} {\sqrt{\frac{2}{\pi (l_1 + l - l_3 - k)}}} \hbox{exp}\left[-\frac{(l_1 - l + l_3 + k)^2} {2 (l_1 + l - l_3 - k)}\right]\\ &\times \sum_{l_4 = 0}^{l_1 + l - l_3 - k} \left(\frac{l_4 (l_1 + l - l_4 - l_3 - k)}{N}\right)^{l_3} e^{-\frac{l_4 (l_1 + l - l_4 - l_3 - k)}{N}} \tilde{z}_{l_4 + l_3} \tilde{z}_{l_1 + l - l_4 - k} \end{aligned} $$

(95)

Defining $x =l/\sqrt{N} , x_1 =l_1/\sqrt{N} , x_4 = l_4/\sqrt{N} ,$ we obtain

$$ \begin{aligned} & p(x) = 2 e^{-\mu} \sum_{l_3 = 0}^{x \sqrt{N}} \frac{1}{l_3!} \frac{\kappa_{l_3}}{\bar{\kappa} + \kappa_{l_3}} \sum_{k = 0}^{x \sqrt{N} - l_3} \frac{\mu^{k}}{k!}\\ &\times \sum_{l_1 = 0}^{N - l} \frac{1}{\sqrt{N}} N^{1/4} {\sqrt{\frac{2}{\pi (x_1 + x)}}} \left[1 - \frac{l_3 + k}{\sqrt{N} (x_1 + x)}\right]^{-1/2} \\ &\times \hbox{exp}\left[-\frac{\sqrt{N} (x_1 - x)^2 + 2 (l_3 + k) (x_1 - x) + \frac{(l_3 + k)^2}{\sqrt{N}}}{2 (x_1 + x) \left(1 - \frac{l_3 + k}{\sqrt{N} (x_1 + x)}\right)}\right]\\ &\times \sum_{l_4 = 0}^{\sqrt{N} (x_1 + x - \frac{l_3 + k} {\sqrt{N}})}\frac{1}{\sqrt{N}} \left(x_4 \left(x_1 + x - x_4 - \frac{l_3 + k} {\sqrt{N}}\right)\right)^{l_3} \\ &\times e^{-x_4 \left(x_1 + x - x_4 - \frac{l_3 + k}{\sqrt{N}}\right)} p\left(x_4 + \frac{l_3}{\sqrt{N}}\right) p\left(x_1 + x - x_4 -\frac{k}{\sqrt{N}}\right) \end{aligned} $$

(96)

and so, for very large N, keeping terms up to order $1/\sqrt{N},$ we obtain

$$\begin{aligned}& p(x) = 2 e^{-\mu} \sum_{l_3 = 0}^{\infty} \frac{1}{l_3!} \frac{\kappa_{l_3}}{\bar{\kappa} + \kappa_{l_3}}\sum_{k = 0}^{\infty} \frac{\mu^{k}}{k!} \int\limits_{0}^{\infty} d x_1 \left(1 + \frac{l_3 + k}{2 \sqrt{N} (x_1 + x)}\right) N^{1/4} {\sqrt{\frac{2}{\pi (x_1 + x)}}}\\ &\times \hbox{exp}\left[-\left(\frac{\sqrt{N} (x_1 - x)^2}{2 (x_1 + x)} + \frac{(l_3 + k) (x_1 - x)}{x_1 + x} + \frac{(l_3 + k)^2}{2 \sqrt{N}(x_1 + x)}\right)\left(1 + \frac{l_3 + k}{\sqrt{N} (x_1 + x)} + \frac{(l_3 + k)^2}{N (x_1 + x)^2}\right)\right]\\ &\times \int\limits_{0}^{x_1 + x} d x_4 [x_4 (x_1 + x - x_4)]^{l_3} \left(1 - \frac{l_3 + k}{\sqrt{N} (x_1 + x - x_4)}\right)^{l_3} e^{-x_4 (x_1 + x - x_4)} e^{x_4 \frac{l_3 + k}{\sqrt{N}}}\\ &\times p\left(x_4 + \frac{l_3}{\sqrt{N}}\right) p\left(x_1 + x - x_4 - \frac{k}{\sqrt{N}}\right)\end{aligned}$$

(97)

Instead of working with p(x) directly, we will work with its Laplace Transform. To this end, we define P(s) = ∫ ^∞₀ p(x)e ^−sx dx. As with the two-chromosomed genome, our strategy will be to take the Laplace Transform of both sides of the above equation, and expand out to order $1/\sqrt{N} .$ This will provide a set of equalities that must be satisfied in the limit of large N, which will allow us to solve for $\bar{\kappa}$ in the N → ∞ limit.

In order to begin, since, in the large N limit, we are assuming that the $\tilde{z}_l$ converge to a Gaussian distribution with a mean that scales as $\sqrt{N}$ and a standard deviation that scales as N ^1/4, we may let ${\lambda}\sqrt{N}$ denote the mean of the distribution and γN ^1/4 denote the standard deviation. If we switch from the l to the x representation, then the Gaussian distribution has a mean of λ and a standard deviation of γN ^−1/4, so that we obtain:

$$ p(x) =\frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\sqrt{N}\frac{(x - \lambda)^2}{2 \gamma^2}\right] $$

(98)

As with the two-chromosomed genome, we have

$$ P(s) = e^{-s \lambda} \left(1 + \frac{\gamma^2}{2 \sqrt{N}} s^2\right) $$

(99)

However, from Eq. 97 we also have that

$$\begin{aligned}& P(s) = 2 e^{-\mu} \sum_{l_3 = 0}^{\infty} \frac{1}{l_3!} \frac{\kappa_{l_3}}{\bar{\kappa} + \kappa_{l_3}} \sum_{k = 0}^{\infty} \frac{\mu^{k}}{k!} \int\limits_{0}^{\infty} dx e^{-s x} \\ &\times \int\limits_{0}^{\infty} d x_1 \left(1 + \frac{l_3 + k}{2 \sqrt{N} (x_1 + x)}\right) N^{1/4} {\sqrt{\frac{2}{\pi (x_1 + x)}}} \hbox{exp}\left[-\frac{\sqrt{N}(x_1 - x)^2}{2 (x_1 + x)}\right]\\ &\times \hbox{exp}\left[-\frac{(l_3 + k) (x_1 - x)}{x_1 + x}\right] \hbox{exp}\left[-\frac{(l_3 + k)^2}{2 \sqrt{N} (x_1 + x)}\right]\hbox{exp}\left[-\frac{(l_3 + k)(x_1 - x)^2}{2 (x_1 + x)^2}\right]\\ &\times \hbox{exp}\left[-\frac{(l_3 + k)^2(x_1 - x)}{\sqrt{N} (x_1 + x)^2}\right] \hbox{exp}\left[-\frac{(l_3 + k)^2 (x_1 - x)^2}{2 \sqrt{N} (x_1 + x)^3}\right]\\ &\times \int\limits_{0}^{x_1 + x} d x_4 [x_4 (x_1 + x - x_4)]^{l_3} \left(1 - \frac{l_3 (l_3 + k)}{\sqrt{N} (x_1 + x - x_4)}\right) e^{-x_4 (x_1 + x - x_4)} \left(1 + x_4 \frac{l_3 + k}{\sqrt{N}}\right)\\ &\times \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2}\left(x_4 - \lambda + \frac{l_3}{\sqrt{N}}\right)^2\right] \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} \left(x_1 + x - x_4 - \lambda - \frac{k}{\sqrt{N}}\right)^2\right] \end{aligned}$$

(100)

Now, define y = x ₁ + x, so that

$$ \begin{aligned} P(s) &= 2 e^{-\mu} \sum_{l_3 = 0}^{\infty} \frac{1}{l_3!} \frac{\kappa_{l_3}}{\bar{\kappa} + \kappa_{l_3}} \sum_{k = 0}^{\infty} \frac{\mu^{k}}{k!} \int\limits_{0}^{\infty} dy\\ &\times \int\limits_{0}^{y} d x e^{-s (x - \frac{y}{2})} e^{-s \frac{y}{2}} \left(1 + \frac{l_3 + k}{2 \sqrt{N} y}\right) N^{1/4} {\sqrt{\frac{2}{\pi y}}} \hbox{exp}\left[-\frac{2 \sqrt{N} (x - \frac{y} {2})^2}{y}\right]\\ &\times \hbox{exp}\left[\frac{2 (l_3 + k)(x - \frac{y}{2})}{y}\right] \hbox{exp}\left[-\frac{(l_3 + k)^2}{2 \sqrt{N} y}\right] \hbox{exp}\left[-\frac{2 (l_3 + k) (x - \frac{y}{2})^2}{y^2}\right]\\ &\times \hbox{exp}\left[\frac{2 (l_3 + k)^2 (x - \frac{y}{2})}{\sqrt{N} y^2}\right] \hbox{exp}\left[-\frac{2 (l_3 + k)^2 (x - \frac{y}{2})^2} {\sqrt{N} y^3}\right]\\ &\times \int\limits_{0}^{y} d x_4 [x_4 (y - x_4)]^{l_3}\left(1 - \frac{l_3 (l_3 + k)}{\sqrt{N}(y - x_4)}\right) \left(1 + x_4 \frac{l_3 + k} {\sqrt{N}}\right) e^{-x_4 (y - x_4)} \\ &\times \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} \left((x_4 - \lambda)^2 + 2 \frac{l_3 (x_4 - \lambda)} {\sqrt{N}} + \frac{l_3^2}{N}\right)\right]\\ &\times \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}} {2 \gamma^2} \left((y - x_4 - \lambda)^2 - 2 \frac{k (y - x_4 - \lambda)}{\sqrt{N}} + \frac{k^2}{N}\right)\right] \end{aligned} $$

(101)

Defining x′ = x − y/2, we obtain, in the limit of large N, that

$$ \begin{aligned} & P(s) = 2 e^{-\mu} \sum_{l_3 = 0}^{\infty} \frac{1}{l_3!}\,\frac{\kappa_{l_3}}{\bar{\kappa} + \kappa_{l_3}} \sum_{k = 0}^{\infty} \frac{\mu^{k}}{k!} \int\limits_{0}^{\infty} dy e^{-s \frac{y}{2}} \left(1 - \frac{(l_3 + k)(l_3 + k - 1)}{2 \sqrt{N} y}\right)\\ &\times \int\limits_{-\infty}^{\infty} d x^{\prime} \left(1 - s x^{\prime} + \frac{1}{2} s^2 x^{\prime 2}\right) \left(1 + \frac{2 (l_3 + k)}{y} x^{\prime} + \frac{2 (l_3 + k)^2}{y^2} x^{\prime 2}\right) \left(1 - \frac{2 (l_3 + k)} {y^2} x^{\prime 2}\right)\\ &\times N^{1/4} {\sqrt{\frac{2}{\pi y}}} \hbox{exp}\left[-\frac{2 \sqrt{N} x^{\prime 2}}{y}\right]\\ &\times \int\limits_{0}^{y} d x_4 [x_4 (y - x_4)]^{l_3} \left(1 - \frac{l_3 (l_3 + k)}{\sqrt{N} (y - x_4)}\right) \left(1 + x_4 \frac{l_3 + k}{\sqrt{N}}\right) e^{-x_4 (y - x_4)}\\ &\times \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}} {2 \gamma^2} \left((x_4 - \lambda)^2 + 2 \frac{l_3 (x_4 - \lambda)}{\sqrt{N}} + \frac{l_3^2}{N}\right)\right]\\ &\times \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} \left((y - x_4 - \lambda)^2 - 2 \frac{k (y - x_4 - \lambda)}{\sqrt{N}} + \frac{k^2}{N}\right)\right] \end{aligned} $$

(102)

In order to evaluate the x′-integral to order $1/\sqrt{N},$ we note that only terms up to $x^{{\prime} {2}}$ will give a contribution that is up to order $1/\sqrt{N},$ and terms of order x′ will integrate out to 0. The integral is then

$$ \begin{aligned} & \int\limits_{-\infty}^{\infty} d x^{\prime} \left(1 + \left(\frac{2 (l_3 + k)^2}{y^2} - \frac{2 (l_3 + k)}{y} s + \frac{1}{2} s^2 - \frac{2 (l_3 + k)}{y^2}\right) x^{\prime 2}\right) N^{1/4} {\sqrt{\frac{2}{\pi y}}}\,\hbox{exp}\left[-\frac{2 \sqrt{N} x^{\prime 2}}{y}\right]\\ & = 1 + \frac{1}{\sqrt{N}} \left(\frac{y}{8} s^2 - \frac{(l_3 + k)}{2} s + \frac{(l_3 + k) (l_3 + k - 1)}{2 y}\right)\\ \end{aligned} $$

(103)

and therefore,

$$ \begin{aligned} & P(s) = 2 e^{-\mu} \sum_{l_3 = 0}^{\infty} \frac{1}{l_3!} \frac{\kappa_{l_3}}{\bar{\kappa} + \kappa_{l_3}} \sum_{k = 0}^{\infty} \frac{\mu^{k}}{k!} \int\limits_{0}^{\infty} d y e^{-s \frac{y} {2}} \left(1 - \frac{(l_3 + k) (l_3 + k - 1)}{2 \sqrt{N} y}\right)\\ &\times \left(1 + \frac{1}{\sqrt{N}} \left(\frac{y}{8} s^2 - \frac{l_3 + k}{2} s + \frac{(l_3 + k) (l_3 + k - 1)}{2 y}\right)\right)\\ &\times \int\limits_{0}^{y} d x_4 [x_4 (y - x_4)]^{l_3} \left(1 - \frac{l_3 (l_3 + k)}{\sqrt{N} (y - x_4)}\right) \left(1 + x_4 \frac{l_3 + k}{\sqrt{N}}\right) e^{-x_4 (y - x_4)}\\ &\times \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} \left((x_4 - \lambda)^2 + 2 \frac{l_3 (x_4 - \lambda)}{\sqrt{N}} + \frac{l_3^2}{N}\right)\right]\\ &\times \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2}\left((y - x_4 - \lambda)^2 - 2 \frac{k (y - x_4 - \lambda)}{\sqrt{N}} + \frac{k^2}{N}\right)\right] \end{aligned} $$

(104)

Defining x ₅ = y − x ₄, we obtain that the double integral over y and x ₄ is,

$$ \begin{aligned} & \int\limits_{0}^{\infty} \int\limits_{0}^{\infty} d x_4 d x_5 e^{-s \frac{x_4 + x_5}{2}} \left(1 + \frac{1}{\sqrt{N}} \left(\frac{x_4 + x_5}{8} s^2 - \frac{l_3 + k}{2} s + x_4 (l_3 + k) - \frac{l_3 (l_3 + k)}{x_5}\right)\right)\\ &\times (x_4 x_5)^{l_3} e^{-x_4 x_5}\\ &\times \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} \left((x_4 - \lambda)^2 + 2 \frac{l_3 (x_4 - \lambda)}{\sqrt{N}} + \frac{l_3^2}{N}\right)\right]\\ &\times \frac{N^{1/4}}{\gamma \sqrt{2 \pi}}\hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} \left((x_5 - \lambda)^2 - 2 \frac{k (x_5 - \lambda)}{\sqrt{N}} +\frac{k^2}{N}\right)\right] \end{aligned} $$

(105)

Now, defining x′₄ = x ₄ − λ, and x′₅ = x ₅ − λ, we have, in the limit of large N, that the integral from −λ to ∞ may be taken to be an integral from −∞ to ∞, because of the narrowness of the Gaussian distribution. Also, any term containing an x ₄ or x ₅ that is coupled to a $1/\sqrt{N}$ factor may have the x ₄ and x ₅ replaced with λ, since for an integral involving x′₄ or x′₅ to survive, it must be on the order of at least $x{^{{\prime} {2}} _{4}}$ or $x{^{{\prime} {2}} _{5}}$. As such integrals produce a $1/\sqrt{N}$ factor or higher, the overall term is of order at least 1/N, which is beyond the order of the expansion we are seeking.

We therefore have that the integral is given by

$$ \begin{aligned} & e^{-s \lambda} e^{-\lambda^2} \lambda^{2 l_3} \left(1 + \frac{1} {\sqrt{N}} \left(\frac{\lambda}{4} s^2 - \frac{l_3 + k}{2} s + \lambda (l_3 + k) - \frac{l_3 (l_3 + k)}{\lambda}\right)\right)\\ &\times \int\limits_{-\infty}^{\infty} \int\limits_{-\infty}^{\infty} d x_4^{\prime} d x_5^{\prime} e^{-s \frac{x_4^{\prime} + x_5^{\prime}}{2}} \left(1 + \frac{x_4^{\prime}}{\lambda}\right)^{l_3} \left(1 + \frac{x_5^{\prime}}{\lambda}\right)^{l_3} e^{-\lambda x_4^{\prime}} e^{-\lambda x_5^{\prime}} e^{-x_4^{\prime} x_5^{\prime}}\\ &\times \hbox{exp}\left[-\frac{l_3 x_4^{\prime}}{\gamma^2}\right] \hbox{exp}\left[-\frac{l_3^2}{2 \sqrt{N} \gamma^2}\right] \hbox{exp}\left[\frac{k x_5^{\prime}}{\gamma^2}\right] \hbox{exp}\left[-\frac{k^2}{2 \sqrt{N} \gamma^2}\right]\\ &\times \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} x_4^{\prime 2}\right] \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} x_5^{\prime 2}\right] \end{aligned} $$

(106)

In order to evaluate this integral, we expand the functions that do not converge to δ-functions in a Taylor series. As we are only interested in terms up to order $1/\sqrt{N},$ we only expand out to order x′ ²₄ or x′ ²₅ . Furthermore, we may neglect any cross terms of $x {^{\prime}_{4}}$ and $x {^{\prime}_{5}}$. The reason for this is that, for such terms to survive, the $x {^{\prime}_{4}}$ term must be coupled to at least another $x {^{\prime}_{4}}$ term, and similarly for the $x {^{\prime}_{5}}$ term. This produces an integral which is of order at least $1/\sqrt{N} {\times}1/\sqrt{N} =1/N ,$ and so may be neglected.

The integral is then

$$ \begin{aligned} & \left(1 - \frac{l_3^2 + k^2}{2 \sqrt{N} \gamma^2}\right) \int\limits_{-\infty}^{\infty} \int\limits_{-\infty}^{\infty} d x_4^{\prime} d x_5^{\prime} \left(1 - \frac{1}{2} \left(x_4^{\prime} + x_5^{\prime}\right) s + \frac{1}{8} \left(x_4^{\prime 2} + x_5^{\prime 2}\right) s^2\right)\\ &\times \left(1 + \frac{l_3}{\lambda} x_4^{\prime} + \frac{l_3 (l_3 - 1)}{2 \lambda^2} x_4^{\prime 2}\right) \left(1 - \lambda x_4^{\prime} + \frac{1}{2} \lambda^2 x_4^{\prime 2}\right) \left(1 - \frac{l_3}{\gamma^2} x_4^{\prime} + \frac{l_3^2}{2 \gamma^4} x_4^{\prime 2}\right)\\ &\times \left(1 +\frac{l_3}{\lambda} x_5^{\prime} + \frac{l_3 (l_3 - 1)} {2 \lambda^2} x_5^{\prime 2}\right) \left(1 - \lambda x_5^{\prime} + \frac{1}{2} \lambda^2 x_5^{\prime 2}\right) \left(1 + \frac{k}{\gamma^2} x_5^{\prime} + \frac{k^2}{2 \gamma^4} x_5^{\prime 2}\right)\\ &\times \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} x_4^{\prime 2}\right] \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} x_5^{\prime 2}\right]\\ & = \left(1 - \frac{l_3^2 + k^2}{2 \sqrt{N} \gamma^2}\right) \int\limits_{-\infty}^{\infty} \int\limits_{-\infty}^{\infty} d x_4^{\prime} d x_5^{\prime} \left(1 - \frac{1}{2} (x_4^{\prime} + x_5^{\prime}) s + \frac{1}{8} (x_4^{\prime 2} + x_5^{\prime 2}) s^2\right)\\ &\times \left(1 + \left(\frac{l_3}{\lambda} - \lambda - \frac{l_3}{\gamma^2}\right) x_4^{\prime} + \left(\frac{l_3^2}{2 \gamma^4} - \frac{l_3^2}{\lambda \gamma^2} + \frac{l_3 \lambda}{\gamma^2} + \frac{1}{2} \lambda^2 - l_3 + \frac{l_3 (l_3 - 1)}{2 \lambda^2}\right) x_4^{\prime 2}\right) \\ &\times \left(1 + \left(\frac{l_3}{\lambda} - \lambda + \frac{k}{\gamma^2}\right) x_5^{\prime} + \left(\frac{k^2}{2 \gamma^4} + \frac{l_3 k}{\lambda \gamma^2} - \frac{k \lambda}{\gamma^2} + \frac{1}{2} \lambda^2 - l_3 + \frac{l_3 (l_3 - 1)}{2 \lambda^2}\right) x_5^{\prime 2}\right)\\ &\times \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}} {2 \gamma^2} x_4^{\prime 2}\right] \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} x_5^{\prime 2}\right] \\ & = \left(1 -\frac{l_3^2 + k^2}{2 \sqrt{N} \gamma^2}\right) \int\limits_{-\infty}^{\infty} \int\limits_{-\infty}^{\infty} d x_4^{\prime} d x_5^{\prime} \left(1 - \frac{1}{2} s x_4^{\prime} + \frac{1}{8} s^2 x_4^{\prime 2} - \frac{1}{2} s x_5^{\prime} + \frac{1}{8} s^2 x_5^{\prime 2}\right)\\ &\times \left(1 + \left(\frac{l_3}{\lambda} - \lambda - \frac{l_3}{\gamma^2}\right) x_4^{\prime} + \left(\frac{l_3^2}{2 \gamma^4} - \frac{l_3^2}{\lambda \gamma^2} + \frac{l_3 \lambda}{\gamma^2} + \frac{1}{2} \lambda^2 - l_3 + \frac{l_3 (l_3 - 1)}{2 \lambda^2}\right) x_4^{\prime 2}\right. \\ & \left.+ \left(\frac{l_3}{\lambda} - \lambda + \frac{k}{\gamma^2}\right) x_5^{\prime} + \left(\frac{k^2}{2 \gamma^4} + \frac{l_3 k}{\lambda \gamma^2} - \frac{k \lambda}{\gamma^2} + \frac{1}{2} \lambda^2 - l_3 + \frac{l_3 (l_3 - 1)}{2 \lambda^2}\right) x_5^{\prime 2}\right)\\ &\times \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} x_4^{\prime 2}\right]\frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} x_5^{\prime 2}\right]\\ & = \left(1 -\frac{l_3^2 + k^2}{2 \sqrt{N} \gamma^2}\right) \int\limits_{-\infty}^{\infty} \int\limits_{-\infty}^{\infty} d x_4^{\prime} d x_5^{\prime}\\ &\times \left(1 + \left(\frac{l_3^2}{2 \gamma^4} - \frac{l_3^2}{\lambda \gamma^2} + \frac{l_3 \lambda}{\gamma^2} + \frac{1}{2} \lambda^2 - l_3 + \frac{l_3 (l_3 - 1)}{2 \lambda^2} - \frac{1}{2} s \left(\frac{l_3}{\lambda} - \lambda - \frac{l_3}{\gamma^2}\right) + \frac{1}{8} s^2\right) x_4^{\prime 2}\right. \\ & \left.+ \left(\frac{k^2}{2\gamma^4} + \frac{l_3 k}{\lambda \gamma^2} - \frac{k\lambda}{\gamma^2} + \frac{1}{2} \lambda^2 - l_3 + \frac{l_3 (l_3 - 1)}{2 \lambda^2} - \frac{1}{2} s \left(\frac{l_3}{\lambda} - \lambda + \frac{k}{\gamma^2}\right) + \frac{1}{8} s^2\right) x_5^{\prime 2}\right)\\ &\times \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} x_4^{\prime 2}\right] \frac{N^{1/4}}{\gamma \sqrt{2 \pi}} \hbox{exp}\left[-\frac{\sqrt{N}}{2 \gamma^2} x_5^{\prime 2}\right]\\ & = 1 + \frac{1}{\sqrt{N}} \left[\frac{l_3 k - l_3^2}{\lambda} + (l_3 - k) \lambda + \lambda^2 \gamma^2 - 2 l_3 \gamma^2 + \frac{l_3 (l_3 - 1) \gamma^2}{\lambda^2}\right] \\ &+ \frac{1}{\sqrt{N}} s \left[\gamma^2 (\lambda - \frac{l_3}{\lambda}) + \frac{1}{2} (l_3 - k)\right] + \frac{1}{\sqrt{N}} \frac{\gamma^2}{4} s^2 \end{aligned} $$

(107)

Going back to Eq. 106, we then have that the overall integral is given by,

$$ \begin{aligned} &e^{-s \lambda} e^{-\lambda^2} \lambda^{2 l_3} \left(1 + \frac{1}{\sqrt{N}}\left [2 l_3 \left(\lambda - \frac{l_3}{\lambda}\right) + \gamma^2 (\lambda^2 - 2 l_3) + \frac{l_3 (l_3 - 1) \gamma^2} {\lambda^2}\right]\right.\\ &\left.+ \frac{1}{\sqrt{N}} \left[\gamma^2 \left(\lambda - \frac{l_3}{\lambda}\right) - k\right] s + \frac{1}{\sqrt{N}} \frac{\lambda + \gamma^2}{4} s^2\right) \end{aligned} $$

(108)

Now, noting that ∑ ^∞ _k=0  μ^k/k! = e ^μ and ∑ ^∞ _{k =0} kμ^k/k! = μe ^μ, we obtain

$$ \begin{aligned} & P(s) = 2 e^{-s \lambda} e^{-\lambda^2} \sum_{l_3 = 0}^{\infty} \frac{1}{l_3!} \frac{\lambda^{2 l_3} \kappa_{l_3}}{\bar{\kappa} + \kappa_{l_3}} \left[1 + \frac{1}{\sqrt{N}} \left(2 l_3 \left(\lambda - \frac{l_3}{\lambda}\right) + \gamma^2 (\lambda^2 - 2 l_3) + \frac{l_3 (l_3 - 1) \gamma^2}{\lambda^2}\right)\right]\\ & + \frac{s}{\sqrt{N}} 2 e^{-s \lambda} e^{-\lambda^2} \sum_{l_3 = 0}^{\infty} \frac{1}{l_3!} \frac{\lambda^{2 l_3} \kappa_{l_3}} {\bar{\kappa} + \kappa_{l_3}} \left[\gamma^2 \left(\lambda - \frac{l_3}{\lambda}\right) - \mu\right] \\ +& \frac{s^2}{\sqrt{N}} \frac{\lambda + \gamma^2}{4} 2 e^{-s \lambda} e^{-\lambda^2} \sum_{l_3 = 0}^{\infty} \frac{1}{l_3!} \frac{\lambda^{2 l_3} \kappa_{l_3}}{\bar{\kappa} + \kappa_{l_3}} \end{aligned} $$

(109)

However, given that, to first order in $1/\sqrt{N},$ we have $P(s) =e^{-s \lambda} (1+\gamma^2/(2 \sqrt{N}) s^2),$ matching powers of s gives us that

$$ \begin{aligned} &1 = 2 e^{-\lambda^2} \sum_{l_3 = 0}^{\infty} \frac{1}{l_3!}\frac{\lambda^{2 l_3} \kappa_{l_3}}{\bar{\kappa} + \kappa_{l_3}}\\ &\times \left[1 + \frac{1}{\sqrt{N}} \left(2 l_3 \left(\lambda - \frac{l_3}{\lambda}\right) + \gamma^2(\lambda^2 - 2 l_3) + \frac{l_3 (l_3 - 1) \gamma^2}{\lambda^2}\right)\right]\\ & 0 = \sum_{l_3 = 0}^{\infty} \frac{1}{l_3!}\frac{\lambda^{2 l_3} \kappa_{l_3}}{\bar{\kappa} + \kappa_{l_3}} \left[\gamma^2 \left(\lambda - \frac{l_3}{\lambda}\right) - \mu\right] \\ & \gamma^2 = (\lambda + \gamma^2) e^{-\lambda^2} \sum_{l_3 = 0}^{\infty} \frac{1}{l_3!} \frac{\lambda^{2 l_3} \kappa_{l_3}}{\bar{\kappa} + \kappa_{l_3}} \end{aligned} $$

(110)

In the limit of large N, the $1/\sqrt{N}$ factor in the first equality becomes negligible, and so we obtain:

$$ \begin{aligned} & 1 = 2 e^{-\lambda^2} \sum_{l_3 = 0}^{\infty} \frac{1}{l_3!} \frac{\lambda^{2 l_3} \kappa_{l_3}}{\bar{\kappa} + \kappa_{l_3}}\\ & 0 = \sum_{l_3 = 0}^{\infty} \frac{1}{l_3!} \frac{\lambda^{2 l_3} \kappa_{l_3}}{\bar{\kappa} + \kappa_{l_3}} \left[\gamma^2 (\lambda - \frac{l_3}{\lambda}) - \mu\right] \\ & \gamma^2 = \frac{\lambda +\gamma^2}{2} \end{aligned} $$

(111)

The last equality implies that γ² = λ, and so, we have that, in the limit of large N, the mean fitness $\bar{\kappa}$ may be obtained by solving the pair of equations,

$$ \begin{aligned} 1 &= 2 e^{-\lambda^2} \sum_{l_3 = 0}^{\infty} \frac{1}{l_3!} \frac{\lambda^{2 l_3} \kappa_{l_3}}{\bar{\kappa} + \kappa_{l_3}}\\ \mu &= \lambda^2 \left(1 - 2 e^{-\lambda^2} \sum_{l_3 = 0}^{\infty} \frac{1}{l_3!} \frac{\lambda^{2 l_3} \kappa_{l_3 + 1}} {\bar{\kappa} + \kappa_{l_3 + 1}} \right)\end{aligned} $$

(112)

As a final calculation for this subsection, we compute, in the limit of large N, the probability that the fusion of two haploids produces a diploid with l homologous gene pairs lacking a functional copy of the given gene. Therefore, suppose two haploids with n defective genes overlap. In order to determine the probability that the overlap produces a diploid with exactly l homologous gene pairs lacking a functional copy of the given gene, we note that, given a haploid, there are $\left(\begin{array}{l}n\\l\\ \end{array}\right)$ ways of placing defective genes in the other haploid so that the diploid has l homologous gene pairs lacking a functional copy of the given gene. The remaining n − l defective genes in the other haploid must be in the N − n slots where the first haploid has a functional copy of the gene. As there are $\left(\begin{array}{l}N - n\\n-l\\ \end{array}\right)$ ways of placing these genes, we obtain that there are a total of $\left(\begin{array}{l}n\\l\\ \end{array}\right)\left(\begin{array}{l}N - n\\n-l\\ \end{array}\right)$ distinct haploid sequences which can fuse with the given haploid to produce a diploid with l homologous gene pairs lacking a functional copy of the given gene. As there are a total of $\left(\begin{array}{l}N\\n\\\end{array}\right)$ distinct haploids having n defective genes, the probability that haploid fusion will lead to a diploid that has exactly l homologous pairs lacking a functional copy of the given gene is,

$$ \frac{\left(\begin{array}{l}n\\ l\\ \end{array}\right)\left(\begin{array}{l} N - n \\ n - l\end{array}\right)} {\left(\begin{array}{l}N\\ n\\ \end{array}\right)} = \frac{1}{l!} \prod_{k = 1}^{l} \frac{(n - l + k)^2}{N - l + k} \prod_{k = 1}^{n - l} \frac{1 + \frac{l + k - 2 n}{N}}{1 - \frac{n - k}{N}} $$

(113)

In the limit of large N, with $n {\rightarrow}{\lambda}\sqrt{N},$ the above expression becomes:

$$ \frac{1}{l!} \lambda^{2 l} \left(1 - \frac{n - l}{N}\right)^{n - l} = \frac{1}{l!} \lambda^{2 l} \left[\left(1 - \frac{n - l}{N}\right)^{-\,\frac{N}{n - l}}\right]^{-\,\frac{(n - l)^2}{N}} \rightarrow \frac{1}{l!} \lambda^{2 l} e^{-\lambda^2} $$

(114)