Introduction

Nowadays, a cleaner and more comfortable living environment is in increasing demand (Almeida-Silva et al. 2020; EzhilKumar et al. 2021). However, the rapid increase in urban population density and consequent urban development cause various problems (Du et al. 2017; Ng 2009). In order to build more buildings in a limited space, modern urban design is developing toward densification-high-rise (Sin et al. 2022; Chen and Mak 2021a). Such a dense urban structure suppresses fresh air circulation and produces a considerable negative impact on citizens (Ming et al. 2021; López-Pérez et al. 2019). First of all, in the crowded street canyon, pedestrians are experiencing thermal discomfort due to the low wind speed (Roth and Chow 2012; Yang et al. 2013; Li et al. 2018; Weerasuriya et al. 2020). In particular, in tropical cities including Hong Kong, many residents are living under severe heat stress due to continuous global warming (Ng and Cheng 2012; Yang and Li 2009). In addition, the low airflow circulation of the street canyon strengthens the stagnation of air pollutants and thus proves disadvantageous in removing traffic pollutants generated in the street (Ai and Mak 2015; Vicente et al. 2018; Li and Gernand 2019). Next, poor ventilation characteristics accelerate the spread of infectious diseases like the COVID-19 pandemic, which poses a great threat to people’s health (Xu et al. 2020; Ahmadi et al. 2020; Pani et al. 2020). Since the above phenomena lead to undesirable and serious consequences for the health of urban residents, a new street canyon design with high airflow circulation capacity is in urgent need. Therefore, improving thermal discomfort and low traffic pollution circulation in urban canyons has been raised as a hot spot problem in recent years (Liu et al. 2016; Du et al. 2018; Huang et al. 2017).

Previous studies reveal that the street canyon structure has a positive effect on airflow circulation inside the canyon (Issakhov et al. 2020; Cui et al. 2021, 2020; Reiminger et al. 2020; Llaguno-Munitxa et al. 2017; Huang et al. 2020, 2022; Zhi et al. 2020). The asymmetric street structure results in weak canyon ventilation capacity, especially in the step-down canyon (Assimakopoulos et al. 2003; Gallagher et al. 2012; Sin et al. 2022; Reiminger et al. 2020). Some studies investigating the effects of street geometric properties (street width ratio and building height ratio) (Xie et al. 2006; Reiminger et al. 2020), street trees (Shen et al. 2022; Sun and Zhang 2018), viaduct (Hao et al. 2019), and solar radiation (Li et al. 2020) on traffic pollution dispersion conclude that street geometric structures have a significant influence on the airflow and pollutant distribution pattern inside the street canyon. Furthermore, the “void deck” building design greatly changes the pedestrian-level wind environment in the canyon and favors the spread of pollutants, providing a cleaner living environment for people (Zhang et al. 2017; Tse et al. 2017; Du et al. 2018; Sha et al. 2018; Chen and Mak 2021a). A void deck is a spatial structure mainly used to relieve heat stress in tropical cities. In this paper, it means an empty space on the first floor of a “lift-up” building. Chew and Norford (2018) conducted a water channel experiment and numerical approaches to study the effect of the first-floor void deck on the wind speed at the pedestrian level in a symmetric street canyon. The results reveal that the street canyon (H/W = 1) with 2–6 m void decks can increase the wind speed at the pedestrian level by 1.2–2.1 times of a regular canyon (0.28 m/s). Thereafter, they reported that the increase in the height of the void deck leads to an increase in wind speed at the pedestrian level, while the effect of increasing the building height on wind speed is insignificant (Chew and Norford 2019). Doubling the height of a building leads to a pedestrian-level wind speed increase of less than 10%. Also, the 4 m void deck is sufficient to improve the pedestrian-level wind speed. Zhang et al. (2019) investigated the effect of void decks on the first and second floors on the personal intake fraction (P_IF) in deep-short street canyons and reported that the first-floor void deck of a high-rise building (H/W = 5) reduced the NO concentration by more than two orders. Chen and Mak (2021b) evaluated pedestrian-level wind comfort around the “lift-up” buildings with non-traditional various configurations. The results showed that void decks can dramatically improve wind comfort around the buildings, and the effect varies greatly depending on the wind direction (0°, 90°, 180°) and building shape. Huang et al. (2022) carried out a 2D numerical simulation for symmetric street canyons and revealed that void decks have significant effects on the airflow structure and pollutant diffusion inside the street canyon. Comparing with the regular street canyon with a main clockwise vortex, the void deck can cause several vortices when a strong stream of air passes through the canyon. This strong airflow provides the most conducive condition to pollutant removal when void decks are located at both buildings. Sin et al. (2022) found that for symmetric canyons, void decks significantly reduce contaminant levels in the canyon. In the void deck canyon, the pollutants are moved by air flowing through the void deck, and in particular, the increased building height produces a more pronounced pollutant removal effect. In this way, the “lift-up” structure not only provides a very advantageous space for people to relax and socialize (Muhsin et al. 2017; Moosavi et al. 2014), but also proves conducive to relieving heat stress and preventing the spread of pollutants and virus transmission by strengthening the wind speed at the pedestrian level (Zhang et al. 2020). As global warming continues, this street design has promising application prospects in improving the ventilation capacity of street canyons in various areas, not limited to tropical areas.

However, there are still many problems to be resolved in the design and application of the “void deck” canyon. Although the actual street canyons are mostly asymmetric canyons, almost all studies have focused on improving the wind speed at the pedestrian respiration level around a single building or in symmetric canyons. The introduction of a void deck in the symmetric street canyon can greatly improve the pollutant ventilation capacity of the canyon, but there are still unclear points for the asymmetric street canyon. Given that more work is needed to find out the extent to which the canyon ventilation capacity is improved according to the void deck location and height in the asymmetrical street structure, and the extent to which the risk of pollutants facing the residents is reduced, this study is to quantitatively explore the in-canyon pollutant ventilation and the exposure risk to the residents according to the height and location of the void deck in the asymmetric street canyon. The indicators that have been thoroughly evaluated here include air exchange rate (ACH), net escape rate (NEV*), mean pollutant concentration (K) for evaluation of the pollutant removal capacity of the canyon with void decks, and the risk level for residents.

Methodology

Street canyon configurations

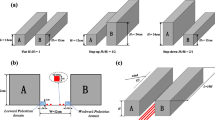
In this study, the 3D regular step-up canyon (R-SUC) and regular step-down canyon (R-SDC) are selected as the reference models for the CFD model validation. Figure 1 illustrates the detailed configurations of the 1:150-scaled regular canyons (RCs). The heights of the two buildings are H and 2H (z direction), respectively, and the width (W, x direction) and length (L, y direction) are the same (W = H = 0.12 m, L = 10H, at the model scale) (Fig. 1a). The street canyon is set as the space between two parallel buildings, where the street width is equal to the building width. That is, the model size (H × W × L) of the street canyon is H × H × 10H. Also, both pedestrian respiration planes (B-PRPs) are set at z = 0.084H (1.5 m at the full scale) inside the canyon. The width of B-PRPs is 0.167H (3 m at the full scale) from both walls of the canyon (Fig. 1b). To mimic traffic exhaust, four-line sources are placed at the distances of 0.23H and 0.35H from both walls, respectively, from which sulfur hexafluoride (SF6) is emitted as a tracer gas. The width and height of each line source are the same (0.042H), and the length is extended by 0.92H each on both laterals to account for vehicle exhaust on the lateral street intersections (Sin et al. 2022; Salim et al. 2011). The wind direction is perpendicular to the canyon (positive x direction). Based on the regular canyons (RCs) mentioned above, taking into account the void deck (VD) location (leeward side, windward side, and both sides) and heights (Hv = H/6 or H/4), 12 asymmetric VD canyons are configured as follows (Fig. 2): the step-up canyon with leeward void deck (L-VD SUC) (Fig. 2a); the step-up canyon with windward void deck (W-VD SUC) (Fig. 2b); the step-up canyon with both void decks (B-VDs SUC) (Fig. 2c); the step-down canyon with leeward void deck (L-VD SDC) (Fig. 2d); the step-down canyon with windward void deck (W-VD SDC) (Fig. 2e); the step-down canyon with both void decks (B-VDs SDC) (Fig. 2f).

Fig. 1
figure 1

Schematic diagram of the regular asymmetric canyon configurations: a R-SUC and R-SDC configurations; b location of B-PRPs and the four-line sources

Full size image
Fig. 2
figure 2

Sketches of the cross-section of the asymmetric VD canyons (Hv = H/6 or H/4): a L-VD SUC; b W-VD SUC; c B-VDs SUC; d L-VD SDC; e W-VD SDC; f B-VDs SDC

Full size image

CFD simulation setups

The CFD domain follows the recommendations in Tominaga et al. (2008) (Fig. 3) and is meshed with the hexahedral grid for all simulation cases. The in-canyon region is meshed by the fine grids (Δx = 0.021H, Δy = 0.083H, and Δz = 0.021H), and the out-canyon region is meshed by the coarser grids, where the maximum grid expansion rate is limited to 1.05. Therefore, the total grid number is approximately 4.5 million. The governing equation for assessing the gas pollutant transport is defined by Eq. (1) (Huang et al. 2022):

$$\overline{{u }_{j}}\frac{\partial C}{{\partial x}_{j}}=\frac{\partial }{{\partial x}_{j}}\left(\left({D}_{m}+{D}_{j}\right)\frac{\partial C}{{\partial x}_{j}}\right)+S$$
(1)

where C is the time-averaged pollutant concentration, and Dm and Dt (Dt = vt/Sct) are respectively the molecular and turbulent diffusivity. Sct is the turbulent Schmidt number and S is the pollutant source term. In this paper, the RANS equations coupled with the standard k-ɛ turbulence model which can well predict the airflow and pollutant dispersion in the 3D long street canyon are chosen (Chew and Norford 2018; Hang et al. 2012; Cui et al. 2016), where Sct is set to 0.3 (Gromke et al. 2008; Huang et al. 2019b; Sin et al. 2022). For Eq. (1), boundary conditions are shown in Fig. 3 and given in Table 1. The residuals below 10−6 are adopted for all variables.

Fig. 3
figure 3

Sketches of the computational domain and boundary conditions

Full size image
Table 1 Summary of boundary conditions
Full size table

CFD validation study by WT experiments

The wind tunnel (WT) experiments are performed in the environmental wind tunnel (length 25 m × height 1.8 m × width 2.5 m) at the University of Shanghai for Science and Technology, with the wind speed control range of 0.1–20 m/s (Fig. 4a). A 3D constant temperature hot-film anemometer (TSI IFA300, ± 0.1% accuracy) is used to provide the atmospheric boundary condition (velocity profile and turbulence intensity) applied to the numerical simulations. Also, the 1:150-scaled isolated canyon model, identical to the one configured in the numerical simulations, is placed in the test section (Fig. 4b). Therefore, reference Re in this study satisfies the Re-independence as 37, 450 (Uehara et al. 2003). As shown in Fig. 4c, WT experimental measurements are taken at the 14 points (1, 2, 3, 5, 7, 9, and 11 cm apart from the floor, respectively) of both walls. The sampling rate of the tracer gas SF6 is adjusted to 0.5 L/min. The SF6 concentration is measured using a SF6 quantitative detector (DB-600T, ± 0.1% accuracy), and is normalized as follows (Huang et al. 2019a):

$$K=\frac{CU\left({z}_{ref}\right)H}{Q/l}$$
(2)

where K is the dimensionless pollutant concentration, C is the SF6 concentration, Q is the emission rate of SF6 (0.83 × 10−5 m3/s), and l is the pollutant injection length. The comparison of WT-measured and CFD-simulated K profiles at 14 measurement points is given in Fig. 5. As shown in Fig. 5, the WT test values on the leeward wall are slightly lower than the numerical simulation values, while it is the opposite on the windward wall. However, CFD and WT simulation results show a relatively satisfactory agreement. From this, it can be noted that the current CFD models and setups (RANS standard k-ɛ model with Sct = 0.3 and 4.5 million grid cells) can guarantee the numerical simulation accuracy. In addition, statistical validation is conducted to evaluate the model performance in the present work. From Table 2 and Table 3, it can be seen that all statistical indicators are within acceptable ranges (Ganguly and Broderick 2010; Santiago et al. 2022). As a result, the present CFD models can sufficiently satisfy the pollutant dispersion within the asymmetric VD canyons.

Fig. 4
figure 4

a Side view of the wind tunnel in the Environmental Wind Tunnel Laboratory of the University of Shanghai for Science and Technology; b SDC model placed on the turntable; c setup of measuring points

Full size image
Fig. 5
figure 5

Comparisons between the WT-measured and CFD-simulated values along the vertical central lines of the leeward wall and windward wall: a R-SUC; b R-SDC

Full size image
Table 2 Summary of statistical indicators for the CFD model performance (the case of R-SUC)
Full size table
Table 3 Summary of statistical indicators for the CFD model performance (the case of R-SDC)
Full size table

Results and discussion

ACH of the canyons

In this paper, the ACH is adopted to evaluate the ventilation capacity of the VD canyons. The ACH has been employed in many previous studies to quantitatively evaluate the amount of air exchanged per unit of time between the canyon and the free stream (Huang et al. 2019a). Here, the ACH of the asymmetric VD canyons is evaluated as follows according to the method proposed by Sin et al. (2022):

$$ACH+=\left({ACH}_{\mathrm{Top}}+\right)+\left({ACH}_{\mathrm{Side}1}+\right)+\left({ACH}_{\mathrm{side}2}+\right)+\left({ACH}_{\mathrm{L}-\mathrm{VD}}+\right)+\left({ACH}_{\mathrm{W}-\mathrm{VD}}+\right)$$
(3)
$$ACH-=\left({ACH}_{\mathrm{Top}}-\right)+\left({ACH}_{\mathrm{Side}1}-\right)+\left({ACH}_{\mathrm{side}2}-\right)+\left({ACH}_{\mathrm{L}-\mathrm{VD}}-\right)+\left({ACH}_{\mathrm{W}-\mathrm{VD}}-\right)$$
(4)

where ACHTop, ACHSide1, ACHSide2, ACHL-VD, and ACHW-VD are the ACH values on the canyon top plane, both sides, and the interfaces between the canyon and void decks where air exchange takes place, respectively. The positive symbol ( +) and negative symbol (-) represent the airflow exiting from the canyon or entering the canyon. The ACH is also divided into the mean component \(\left(\overline{ACH }\right)\) and the turbulence component (ACH′), where the turbulence component (ACH′) is given as follows (Li et al. 2005):

$$ACH=\overline{ACH }+{ACH}^{^{\prime}}$$
(5)
$${ACH}_{\mathrm{Top}}^{^{\prime}}+=-{ACH}_{\mathrm{Top}}^{^{\prime}}-=\frac{1}{\sqrt{6}}\underset{{\Gamma }_{1}}{\overset{}{\int }}{\sqrt{kd\Gamma }}_{1}$$
(6)
$${ACH}_{\mathrm{Side}1}^{^{\prime}}+=-{ACH}_{\mathrm{Side}1}^{^{\prime}}-=\frac{1}{\sqrt{6}}\underset{{\Gamma }_{2}}{\overset{}{\int }}{\sqrt{kd\Gamma }}_{2}$$
(7)
$${ACH}_{\mathrm{Side}2}^{^{\prime}}+=-{ACH}_{\mathrm{Side}2}^{^{\prime}}-=\frac{1}{\sqrt{6}}\underset{{\Gamma }_{3}}{\overset{}{\int }}{\sqrt{kd\Gamma }}_{3}$$
(8)
$${ACH}_{\mathrm{L}-\mathrm{VD}}^{^{\prime}}+=-{ACH}_{\mathrm{L}-\mathrm{VD}}^{^{\prime}}-=\frac{1}{\sqrt{6}}\underset{{\Gamma }_{4}}{\overset{}{\int }}{\sqrt{kd\Gamma }}_{4}$$
(9)
$${ACH}_{\mathrm{W}-\mathrm{VD}}^{^{\prime}}+=-{ACH}_{\mathrm{W}-\mathrm{VD}}^{^{\prime}}-=\frac{1}{\sqrt{6}}\underset{{\Gamma }_{5}}{\overset{}{\int }}{\sqrt{kd\Gamma }}_{5}$$
(10)

where Γ1 = L × W, Γ2 = Γ3 = H × W, Γ4 = Γ5 = Hv × L are the areas of each air exchange plane. Figure 6 displays the change in the ACH of the asymmetric VD canyons. Table 4 and Table 5 tabulate the positive and negative dimensionless ACH values. From Fig. 6, the following characteristics are obtained from the ACH change of asymmetric canyons according to different VD locations and heights.

Fig. 6
figure 6

ACH of the asymmetric VD canyons

Full size image
Table 4 Positive dimensionless ACH + values of the asymmetric VD canyons
Full size table
Table 5 Negative dimensionless ACH- values of the asymmetric VD canyons
Full size table
  1. 1.

    The ACH values of the asymmetric VD canyons are significantly increased compared to the RCs (except for the case of L-VD SUCs), especially for the SDCs (Fig. 6). For the case of the SUCs, the ACH values of B-VDs SUCs have the greatest increase, followed by the W-VD SUCs. When the VD height is H/6, the ACH values of B-VDs SUC and W-VD SUC increase significantly compared to the R-SUC (Table 5). For the W-VD SUC (Hv = H/6), the airflow component (ACHTOP-) is the highest compared to the R-SUC, but the airflow component (ACHW-VD) is much lower than the airflow component (ACHL-VD-) of B-VDs SUC (Table 5). Therefore, the ACH (148.1% of the R-SUC) of the B-VD SUC is slightly higher than that (139.6%) of W-VD SUC and has the maximum ACH. For the L-VD SUC, although there is airflow entering through the L-VD, the airflow component (ACHTOP-) is much smaller than the R-SUC (Table 5). Therefore, the ACH of the L-VD SUC stays at the minimum level (94.5% of the R-SUC). For the SDCs, the ACH values of the L-VD SDCs and B-VDs SDCs increase dramatically. For the L-VD SDC (Hv = H/6), the airflow components (ACHTOP- and ACHL-VD-) increase substantially compared to that of the R-SDC (Table 5). The ACH of the L-VD SDC is the largest, 310.9% of the R-SDC. For B-VD SDC (Hv = H/6), the airflow component (ACHL-VD-) is almost equal to that of the L-VD SDC, but the airflow component (ACHTOP-) is lower. The ACH is smaller than that of the L-VDC (278.8% of the R-SDC). The W-VD SDC (Hv = H/6) has the lowest ACH value (132.9%) because the airflow components (ACHTOP- and ACHW-VD-) are much lower than the above two cases.

  2. 2.

    The ACH values of the asymmetric VD canyons increase significantly as the VD height increases (Fig. 6). The effect of increasing the VD height is evident for the W-VD SUC and B-VDs SUC, and remains inconspicuous for the L-VD SUC. For the W-VD SUC and B-VDs SUC (Hv = H/4), the airflow components entering through the canyon top plane and VDs grow significantly, compared to the corresponding canyons with lower VD height (Hv = H/6) (Table 5). However, for the L-VD SUC (Hv = H/4), the airflow component (ACHTOP-) decreases, while the airflow component (ACHL-VD-) increases. Therefore, the ACH values of W-VD SUC and B-VDs SUC increase dramatically by 157.2% and 177.4%, respectively, compared to the R-SUC, whereas for the L-VD SUC, ACH increases slightly (101%). The effect of increasing the VD height is pronounced for the L-VD SDC and B-VDs SDC and weak for the W-VD SDC. For the L-VD SDC (Hv = H/4), the airflow component (ACHTOP-) is lower compared to that of the L-VD SDC (Hv = H/6), but the airflow component (ACHL-VD-) is much higher. For B-VDs SDC (Hv = H/4), the airflow components (ACHTOP- and ACHW-VD-) are much higher compared to that of B-VDs SDC (Hv = H/6). However, for the W-VD SDC (Hv = H/4), compared to the W-VD SDC (Hv = H/6), the airflow component (ACHTOP-) decreases, while the airflow component (ACHW-VD-) increases. Therefore, when the VD height is H/4, the ACH values of the L-VD SDC, W-VD SDC, and B-VDs SDC are 390.3%, 161.5%, and 392.5% of the R-SDC, respectively, presenting more significant increases than when the VD height is H/6.

  3. 3.

    The turbulence component (ACH′) of the asymmetric VD canyons (except for the case of L-VD SUCs) declines compared to the RCs, especially for the SDCs (Table 4). For the W-VD SUC and B-VDs SUC, the mean components entering through the canyon top plane and VDs grow remarkably compared to the R-SUC. However, for the L-VD SUC, the mean component \(\left({\overline{ACH} }_{\mathrm{TOP}-}\right)\) is much lower than that of the R-SUC. Therefore, the turbulence components (ACH′) decrease for the W-VD SUC and B-VDs SUC and increase for the L-VD SUCs. For the SUCs, the mean component \(\left(\overline{ACH }-\right)\) is the highest for the case of B-VDs, followed by the case of the W-VD. For the W-VD SDCs, the mean component \(\left({\overline{ACH} }_{\mathrm{TOP}-}\right)\) is lower than the R-SDC (for the L-VD SDC and B-VDs SDC, the mean components are much higher than the R-SDC), but the mean component \(\left({\overline{ACH} }_{\mathrm{W}-\mathrm{VD}-}\right)\) is much higher, so the mean component \(\left(\overline{ACH }-\right)\) increases while the turbulence component (ACH′) decreases. For the SDCs, the mean component is the highest for the case of the L-VD (Hv = H/6) and B-VDs (Hv = H/4).

As shown in Fig. 6, the ACH values are similar for B-VDs SDC and L-VD SDC (for the case of Hv = H/4). However, there is a significant difference in the residual amount of pollutants in the canyon, as can be seen from Figs. 7, 8, and 9e and g and Figs. 10, 11, and 12e and g, suggesting that ACH explains well the mean flow and turbulence flow entering or exiting the canyon, but not pollutant transport. This is because, for the asymmetric VD canyons (especially B-VDs canyons), pollutants are directly affected by the airflow entering or exiting through VDs. Therefore, in the next subsection, the pollutant ventilation capacity of canyons with VDs is quantitatively evaluated.

Fig. 7
figure 7

NEV* of the asymmetric VD canyons

Full size image
Fig. 8
figure 8figure 8

Airflow and K patterns at the vertical central planes of the SUCs: a R-SUC; b L-VD SUC & Hv = H/6; c W-VD SUC & Hv = H/6; d B-VDs SUC & Hv = H/6; e L-VD SUC & Hv = H/4; f W-VD SUC & Hv = H/4; g B-VDs SUC & Hv = H/4

Full size image
Fig. 9
figure 9figure 9

Airflow and K patterns at the vertical central planes of the SDCs: a R-SDC; b L-VD SDC & Hv = H/6; c W-VD SDC & Hv = H/6; d B-VDs SDC & Hv = H/6; e L-VD SDC & Hv = H/4; f W-VD SDC & Hv = H/4; g B-VDs SDC & Hv = H/4

Full size image
Fig. 10
figure 10

The mean K ( KL and KW) on B-PRPs of the asymmetric VD canyons: a L-PRP; b W-PRP

Full size image
Fig. 11
figure 11

Airflow and K patterns at the pedestrian respiration height of the SUCs: a R-SUC; b L-VD SUC & Hv = H/6; c W-VD SUC & Hv = H/6; d B-VDs SUC & Hv = H/6; e L-VD SUC & Hv = H/4; f W-VD SUC & Hv = H/4; g B-VDs SUC & Hv = H/4

Full size image
Fig. 12
figure 12

Airflow and K patterns at the pedestrian respiration height of the SDCs: a R-SDC; b L-VD SDC & Hv = H/6; c W-VD SDC & Hv = H/6; d B-VDs SDC & Hv = H/6; e L-VD SDC & Hv = H/4; f W-VD SDC & Hv = H/4; g B-VDs SDC & Hv = H/4

Full size image

NEV* of the canyons

The NEV concept was first proposed by Lim et al. (2013), as an index representing the pollutant transport effects from a target point considering both convection and diffusion. Thereafter, NEV was modified by Hang et al. (2015) as the normalized escape velocity (NEV*) of pollutants removed/diluted from the street canyon as follows:

$${NEV}^{*}=\frac{S\bullet V\bullet A}{<c>\bullet {U}_{ref}}$$
(11)

where S is the pollutant emission rate, V is the canyon volume, A is the area of the canyon top plane, and < c > is the volume-average pollutant concentration of the entire canyon. Figure 7 illustrates the change in NEV* of the asymmetric street canyons according to the VD location and height. The NEV* of asymmetric VD canyons is significantly increased compared to the RCs. For the SUCs, the NEV* of B-VDs canyons have the greatest increase, followed by the W-VD canyons. When the VD height is H/6, the NEV* of B-VDs SUC, W-VD SUC, and L-VD SUC are 4.17 times, 1.69 times, and 1.17 times, respectively. For the SDCs, the growth of NEV* is the highest (9.16 times) for B-VDs SDC, followed by the L-VD SDC (3.63 times), and the lowest (1.76 times) for the W-VD SDC. In other words, B-VDs canyons have the best pollutant ventilation capacity. Additionally, the NEV* of the asymmetric VD canyons increases along with the VD height, with the most significant growth for B-VDs canyons. When the VD height is H/4, the NEV* of B-VDs SUC goes up by 5.95 times, the W-VD SUC by 2.01 times, and the L-VD SUC by 1.4 times, compared to the RCs. For the SDCs, the NEV* of B-VDs SDC increases by 12.7 times, the L-VD SDC by 5.11 times, and the W-VD SDC by 2.11 times. As seen in the NEV* analysis, VDs can significantly improve the pollutant ventilation capacity of asymmetric canyons, which is especially suitable for SDCs with poor ventilation conditions.

Airflow and pollutant distributions on the canyon vertical central plane

Figures 8 and 9 show the airflow and pollutant distribution patterns at the vertical central plane of the asymmetric VD canyons. For the R-SUC, most of the pollutants are accumulated near the leeward wall due to the large clockwise vortex formed inside the canyon, and for the R-SDC, pollutants are mostly accumulated near the windward wall due to the counterclockwise vortex (Figs. 8a and 9a). Moreover, the ACH of the R-SDC is much lower than that of the R-SUC (Fig. 6), so more pollutants accumulate inside the R-SDC. From Figs. 8 and 9, it can be seen that the airflow and pollutant distribution in the asymmetric VD canyons are significantly different from those of the RCs.

  1. 1.

    The VD location has a great impact on the airflow and pollutant distribution inside the asymmetric canyons, and the pollutant concentration (K) at the vertical central plane of the canyons declines substantially compared to the RCs. As shown in Figs. 8 and 9, the asymmetric VD canyons have lower K than the RCs because they facilitate pollutant movement by allowing additional airflow entering/exiting the canyon through the VDs. Also, in all asymmetric VD canyons, except for the W-VD SUCs, the pollutants generated from the canyon floor are transported by the airflow that comes in through the VDs. For B-VDs canyons (Fig. 8d and g, Fig. 9d and g), pollutants are removed from the canyon by strong airflow (as shown in Table 5, in these cases, the airflow component entering through the L-VD is the highest compared to other cases) passing the shortest section through B-VDs. Therefore, the K of B-VDs canyons is the lowest. For the L-VD SUCs (Fig. 8b and e), pollutants move upward the canyon by the airflow coming through the L-VD, and for the W-VD SUCs (Fig. 8c and f), pollutants move toward the leeward wall by a clockwise vortex formed in the canyon. For the two cases, the K of the W-VD SUCs is lower than that of the L-VD SUCs. This is because, for the L-VD SUCs, the airflow flowing upward the canyon through the L-VD and the airflow entering the canyon through the canyon top plane are opposite in direction, thus suppressing the elimination of pollutants from the canyon. For the L-VD SDCs (Fig. 9b and e), pollutants are moved to the windward wall by the strong airflow coming through the L-VD and then easily removed out of the canyon as the downwind building is low. However, for the W-VD SDCs (Fig. 9c and g), the diffusion of pollutants by the relatively weak airflow (back-airflow of the free stream) coming through the W-VD is suppressed by the airflow coming through the canyon top plane. Therefore, the K of the L-VD SDCs is lower than that of the W-VD SDCs.

  2. 2.

    The K on the vertical central plane of the canyons reduces slightly as the VD height increases. From Figs. 8 and 9, it can be seen that the increased VD height brings about slightly stronger airflow entering or exiting through VDs. For the L-VD SUC (Hv = H/4), a part of the airflow entering through the L-VD flows upward the canyon along the windward wall due to the increase in the airflow strength. Therefore, the K is slightly lower than that of the L-VD SUC (Hv = H/6) (Fig. 8b and e). For the W-VD SUC (Hv = H/4), as a result of the strong airflow out of the canyon through the W-VD after passing over the roof of the upwind building, the vortex strength inside the canyon is slightly stronger, so the K is reduced as the VD height goes up (Fig. 8c and f). For B-VD SUC (Hv = H/4), the airflow exiting through the W-VD is stronger and the K inside the canyon is lower accordingly (Fig. 8d and g). Likewise, for the SDCs with VDs (Fig. 9b–g), the airflow strength entering or exiting through the VDs grows as the VD height rises, and thus the K inside the canyons is lower than that in cases with lower VD height (Hv = H/6).

Pollutant distribution at the pedestrian respiration level

From Fig. 10, the mean K changes on both pedestrian respiration planes (B-PRPs) of the asymmetric VD canyons are characterized as follows:

  1. 1.

    For the SUCs, the KL is reduced compared to the R-SUC and drops to almost zero when VDs are at the upwind building or both buildings. The KW decreases slightly when VDs are at the downwind building or both buildings and increases significantly for the L-VD SUCs. As shown in Fig. 11a, for the R-SUC, more pollutants are accumulated on the L-PRP than on the W-PRP due to the large clockwise vortex formed inside the canyon. However, for the L-VD SUC (Hv = H/6), pollutants are accumulated near the windward wall by the airflow that enters through the L-VD and then flows toward the downwind building (Fig. 11b). Therefore, the KA is almost equal to zero, while the KB increases compared to the R-SUC (404.5%). For the W-VD SUC (Hv = H/6), the airflow near the windward wall splits in two directions by the airflow exiting through the W-VD and the vortex component created inside the canyon (Fig. 11c). Part of the pollutants are removed from the canyon by the airflow exiting through the W-VD, and the rest are carried to the leeward wall by the vortex component. As a result, the K on B-PRPs goes down compared to the R-SUC (KA = 63%, KB = 79.1%, respectively). For B-VDs SUC (Hv = H/6), the airflow entering through the L-VD goes out of the canyon directly through the W-VD, removing almost all the pollutants from the canyon (Fig. 11d). Therefore, the KA is almost equal to zero, and the KB slightly decreases compared to the R-SUC (KB = 97%).

  2. 2.

    For the SDCs, the K is almost zero when VDs are at the upwind building or both buildings, and for the W-VD SDCs, it increases significantly in contrast with the R-SDC. The KB is more significantly reduced than that of the R-SDC. For the R-SDC (Fig. 12a), more pollutants are accumulated on the windward wall than on the leeward wall by the counterclockwise vortex formed inside the canyon, meaning that the KB is higher than the KA. However, for the L-VD SDC (Hv = H/6), the strong airflow entering through the L-VD moves the pollutants toward the windward wall and then moves upward toward the canyon (Figs. 12b and 9b). Hence, the KA is almost equal to zero and the KB is significantly reduced compared to the R-SDC (KB = 42.4%). For the W-VD SDC (Hv = H/6), pollutants are moved toward the leeward wall by the airflow entering through the W-VD (Figs. 12c and 9c), resulting in an increased KA compared to the R-SDC and a dramatically reduced KB (KA = 208.2%, KB = 1.4%, respectively). For B-VDs SDC (Hv = H/6), pollutants are removed from the canyon by the strong airflow passing through B-VDs (Figs. 12d and 9d), and accordingly, the KA is almost equal to zero and the KB is also significantly reduced compared to the R-SDC (KB = 16.1%).

  3. 3.

    The increase in the VD height reduces significantly the K on B-PRPs of the asymmetric VD canyons. For asymmetric VD canyons, pollutants are removed from the canyon by the airflow passing the canyon bottom, with the exception of the W-VD SUCs (see Figs. 8 and 9). Therefore, as the VD height increases, the airflow entering the canyon through VDs becomes stronger (Table 4), thus eliminating more pollutants and resulting in the lower K on B-PRPs of the canyon. As shown in Fig. 10a, the KLW of the W-VD SUCs and W-VD SDCs decreases with increasing VD height. For the W-VD SUCs (Fig. 8c and f), the airflow exiting through the W-VD grows stronger as the VD height increases and brings about a stronger vortex. The pollutants accumulating near the leeward wall are reduced by the enhanced clockwise vortex, and the KA goes down from 63% of the R-SUC to 53.9%. For the W-VD SDCs, the airflow entering through the W-VD becomes stronger as the VD height increases, allowing more pollutants to be removed from the canyon along the leeward wall (Fig. 9c and f). Accordingly, the KA decreases from 208.2% of the R-SDC to 159.8%. The KB of the asymmetric VD canyons decreases with increasing VD height, as shown in Fig. 10b. The KB of the W-VD SUCs is affected by the airflow downward the windward wall before it exits through the W-VD (Fig. 8c and f). The strength of this airflow grows along with the VD height, removing more pollutants from the canyon and further reducing the KB.

Figure 13 displays the change in the K on the W-VD pedestrian respiration planes of the W-VD canyons and B-VD canyons. For these cases, the pollutants are partially accumulated under the downwind building by the airflows entering the W-VD. Most pollutants accumulate near the leeward wall for the W-VD canyons (Fig. 11c and d, Fig. 12c and d), whereas most pollutants are moved toward the W-VD for B-VDs canyons. Therefore, the mean K on the W-VD pedestrian respiration planes of B-VDs canyons is higher than that of the W-VD canyons, and the mean K on the W-VD pedestrian respiration planes decreases as the VD height increases due to the stronger airflow exiting through the W-VD.

Fig. 13
figure 13

Mean K on the W-VD pedestrian respiration planes

Full size image

Pollutant distribution on the canyon walls

Figure 14 presents the mean K on both walls of the asymmetric VD canyons. Figures 15 and 16 display the K patterns on both walls of the asymmetric VD canyons. From Fig. 14, it can be seen that the K on both walls changes significantly with VD locations, and the K on both walls decreases due to the enhanced airflow entering the canyon as the VD height increases.

  1. 1.

    The K on both walls of the SUCs is significantly reduced compared to the R-SUC, except for the KWW of the L-VD SUCs (Fig. 14). From Fig. 15a, for the R-SUC, the KLW are higher than the KWW because more pollutants accumulate on the leeward wall due to the clockwise vortex. However, for the L-VD SUCs (Fig. 15b and e), pollutants are removed upward the canyon by the airflow going upward the windward wall after entering through the L-VD. Therefore, compared to the R-SUC, the KLW diminishes by 23.8% and 17.2%, respectively. On the contrary, the KWW increases by 457.1% and 419.0%, since pollutants cannot be easily removed beyond the canyon due to the taller downwind building. For the W-VD SUCs (Fig. 15c and f), the KLW is higher than the KWW as pollutants are moved toward the leeward wall by the clockwise vortex. However, since most pollutants are removed from the canyon through the W-VD, the K on both walls is reduced compared to the R-SUC (KLW = 56.3%, 46.4%; KWW = 33.3%, 23.8%). For B-VDs SUCs (Fig. 15d and g), the K on both walls is lowest compared to the R-SUC, as pollutants are removed by the airflow going out of the canyon directly through B-VDs (KLW = 6.6%, 3.3%; KWW = 19.0%, 9.5%).

  2. 2.

    The K on both walls of the SDCs significantly decreases compared to the R-SDC, except for the KLW of the W-VD SDCs (Fig. 14). For the R-SDC (Fig. 16a), the KWW is higher than the KLW due to the counterclockwise vortex inside the canyon. For the L-VD SDCs (Fig. 16b and e), pollutants are moved upward the canyon by an airflow that enters through the L-VD and then flows upward the canyon along the windward wall. Therefore, the KLW is substantially reduced (47.3%, 29.7%) compared to the R-SDC and the KWW is also reduced (48.1%, 35.0%) because pollutants are easily carried upward the canyon as a result of the low height of the downwind building. For the W-VD SDCs (Fig. 16c and f), most pollutants accumulate on the leeward wall due to the weak airflow entering through the W-VD. Therefore, the KWW is significantly reduced (19.4%, 14.3%), but the KLW (224.3%, 187.8%) is higher than that of the R-SDC. This is attributable to the fact that the pollutants can hardly be carried upward the canyon by the airflow due to the taller upwind building. For B-VDs SDCs (Fig. 16d and g), pollutants are removed by the airflow passing through B-VDs, so the K on both walls is significantly diminished in contrast with the R-SDC (KLW = 14.9%, 10.8%; KWW = 11.8%, 7.2%).

Fig. 14
figure 14

Mean K at both walls of the asymmetric VD canyons: a leeward wall; b windward wall

Full size image
Fig. 15
figure 15

Mean K patterns on the leeward wall (A) and windward wall (B) of the SUCs: a R-SUC; b L-VD SUC & Hv = H/6; c W-VD SUC & Hv = H/6; d B-VDs SUC & Hv = H/6; e L-VD SUC & Hv = H/4; f W-VD SUC & Hv = H/4; g B-VDs SUC & Hv = H/4

Full size image
Fig. 16
figure 16

Mean K patterns at the leeward wall (A) and windward wall (B) of the SDCs: a R-SDC; b L-VD SDC & Hv = H/6; c W-VD SDC & Hv = H/6; d B-VDs SDC & Hv = H/6; e L-VD SDC & Hv = H/4; f W-VD SDC & Hv = H/4; g B-VDs SDC & Hv = H/4

Full size image

Conclusions

In this paper, we have evaluated the effects of VD height and location on ventilation and pollutant dispersion in asymmetric street canyons. Numerical simulation results show that VDs have significant effects on canyon ventilation and pollutant dispersion. The major findings are summarized as follows:

  1. 1.

    VDs can significantly improve the ventilation performance of the asymmetric canyons by introducing more fresh air compared to the RCs. In contrast with the RCs, the ACH values (147.9%, 177.3%; 270.9%, 380.9%) and NEV* (416.7%, 595.2%; 915.8%, 1268.4%) of B-VDs SUCs and SDCs undergo the greatest increase, followed by W-VD SUCs and L-VD SDCs. In particular, the VD proves suitable for the design of the SDC because it can dramatically enhance the ventilation capacity of the SDC.

  2. 2.

    Depending on the VD location, the flow field inside the asymmetric canyons has a distinct modification. For the asymmetric VD canyons, the K on the building wall and PRP in which VDs are located is very low because pollutants are removed by the airflow entering or exiting through VDs. Therefore, among the three VD locations, B-VDs can provide an optimal living environment for pedestrians and near-road residents, followed by W-VD SUCs and L-VD SDCs.

  3. 3.

    Increases in the VD height could enhance the airflow entering or exiting from the canyon, thus offering a more favorable environment for pollutant dispersion inside the canyons. The higher VD height results in better canyon ventilation and lower K on the canyon walls and B-PRPs. Therefore, the K on B-PRPs and both walls is significantly reduced as the VD height increases and remains at a very low level for B-VDs canyons. The 3–4.5 m high VD can greatly improve the ventilation capacity of asymmetric canyons and significantly reduce the pollutant exposure risk level of pedestrians and residents.

  4. 4.

    Similar to the symmetric canyons (Sin et al. 2022), the ventilation capacity of asymmetric canyons increases significantly with increasing VD height and the pollutant exposure risk levels are greatly reduced. In addition, for the symmetric canyons, the canyon with B-VDs has the highest ACH and NEV*, followed by the canyon with the L-VD. However, for the step-up canyons, the canyon with B-VDs has the highest ACH and NEV*, followed by the canyon with W-VD.

This paper provides a scientific foundation for building healthy and sustainable urban environments by presenting quantitative evaluations of the asymmetric street canyon design, which can significantly mitigate the traffic pollutant risk for pedestrians and residents in cities located in tropical regions, such as Hong Kong and Singapore.