Skip to main content

Advertisement

Springer Nature Link
Log in

A Critical Review of Surrogate Assisted Robust Design Optimization

  • Original Paper
  • Published:
Archives of Computational Methods in Engineering Aims and scope Submit manuscript

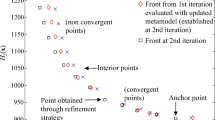
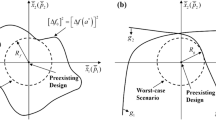
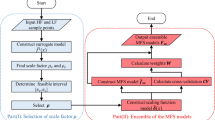
Abstract

Robust design optimization (RDO) has been eminent, ascertaining optimal configuration of engineering systems in presence of uncertainties. However, computational aspect of conventional RDO can often get computationally intensive as neighborhood assessments of every solution are required to compute the performance variance and ensure feasibility. Surrogate assisted optimization is one of the efficient approaches in order to mitigate this issue of computational expense. However, the performance of a surrogate model plays a key factor in determining the optima in multi-modal and highly non-linear landscapes, in presence of uncertainties. In other words, the approximation accuracy of the model is principal in yielding the actual optima and thus, avoiding any misguide to the decision maker on the basis of false or, local optimum points. Therefore, an extensive survey has been carried out by employing most of the well-known surrogate models in the framework of RDO. It is worth mentioning that the numerical study has revealed consistent performance of a model out of all the surrogates utilized. Finally, the best performing model has been utilized in solving a large-scale practical RDO problem. All the results have been compared with that of Monte Carlo simulation results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Jin R, Du X, Chen W (2003) The use of metamodeling techniques for optimization under uncertainty. Struct Multidiscip Optim 25:99–116

    Google Scholar 

  2. Zang C, Friswell MI, Mottershead JE (2005) A review of robust optimal design and its application in dynamics. Comput Struct 83:315–326

    Google Scholar 

  3. Beyer H-G, Sendhoff B (2007) Robust optimization: a comprehensive survey. Comput Methods Appl Mech Eng 196:3190–3218

    MathSciNet  MATH  Google Scholar 

  4. Chen W, Allen J, Tsui K, Mistree F (1996) Procedure for robust design: minimizing variations caused by noise factors and control factors. J Mech Des Trans ASME 118:478–485

    Google Scholar 

  5. Du X, Chen W (2000) Towards a better understanding of modeling feasibility robustness in engineering design. J Mech Des Trans ASME 122:385–394

    Google Scholar 

  6. Huang B, Du X (2007) Analytical robustness assessment for robust design. Struct Multidiscip Optim 34:123–137

    Google Scholar 

  7. Phadke M (1989) Quality engineering using robust design. Prentice Hall, Englewood Cliffs, NJ

    Google Scholar 

  8. Taguchi G (1987) System of experimental design: engineering methods to optimize quality and minimize costs, vol 1, UNIPUB/Kraus International Publications, White Plains, NY

    Google Scholar 

  9. Taguchi G (1986) Quality engineering through design optimization. Krauss International Publications, White Plains, NY

    Google Scholar 

  10. Alexandrov N, Lewis R (2002) Analytical and computational aspects of collaborative optimization for multidisciplinary design. AIAA J 40:301–309

    Google Scholar 

  11. Hicks R, Henne PA (1978) Wing design by numerical optimization. J Aircr 15:407–412

    Google Scholar 

  12. Sobieszczanski-Sobieski J, Haftka R (1997) Multidisciplinary aerospace design optimization: survey of recent developments. Struct Optim 14:1–23

    Google Scholar 

  13. Fang J, Gao Y, Sun G, Li Q (2013) Multiobjective reliability-based optimization for design of a vehicle door. Finite Elem Anal Des 67:13–21

    Google Scholar 

  14. Hwang K, Lee K, Park G (2001) Robust optimization of an automobile rearview mirror for vibration reduction. Struct Multidiscip Optim 21:300–308

    Google Scholar 

  15. Sun G, Li G, Zhou S, Li H, Hou S, Li Q (2010) Crashworthiness design of vehicle by using multiobjective robust optimization. Struct Multidiscip Optim 44:99–110

    Google Scholar 

  16. Diez M, Peri D (2010) Robust optimization for ship conceptual design. Ocean Eng 37:966–977

    Google Scholar 

  17. Hart CG, Vlahopoulos N (2009) An integrated multidisciplinary particle swarm optimization approach to conceptual ship design. Struct Multidiscip Optim 41:481–494

    Google Scholar 

  18. Parsons M, Scott R (2004) Formulation of multicriterion design optimization problems for solution with scalar numerical optimization methods. J Sh Res 48:61–76

    Google Scholar 

  19. Doltsinis I, Kang Z (2004) Robust design of structures using optimization methods. Comput Methods Appl Mech Eng 193:2221–2237

    MATH  Google Scholar 

  20. Lagaros ND, Plevris V, Papadrakakis M (2007) Reliability based robust design optimization of steel structures. Int J Simul Multidiscip Des Optim 1:19–29

    Google Scholar 

  21. Lee SH, Chen W, Kwak BM (2009) Robust design with arbitrary distributions using Gauss-type quadrature formula. Struct Multidiscip Optim 39:227–243

    MathSciNet  MATH  Google Scholar 

  22. Cheng J, Liu Z, Wu Z, Li X, Tan J (2014) Robust optimization of structural dynamic characteristics based on adaptive Kriging model and CNSGA. Struct Multidiscip Optim 51:423–437

    Google Scholar 

  23. Roy BK, Chakraborty S (2015) Robust optimum design of base isolation system in seismic vibration control of structures under random system parameters. Struct Saf 55:49–59

    Google Scholar 

  24. Lee T, Jung J (2006) Metamodel-based shape optimization of connecting rod considering fatigue life. Key Eng Mater 211:306–308

    Google Scholar 

  25. Li F, Meng G, Sha L, Zhou L (2011) Robust optimization design for fatigue life. Finite Elem Anal Des 47:1186–1190

    Google Scholar 

  26. McDonald M, Heller M (2004) Robust shape optimization of notches for fatigue-life extension. Struct Multidiscip Optim 28:55–68

    Google Scholar 

  27. Lee I, Choi KK, Du L, Gorsich D (2008) Dimension reduction method for reliability-based robust design optimization. Comput Struct 86:1550–1562

    MATH  Google Scholar 

  28. Ramakrishnan B, Rao S (1996) A general loss function based optimization procedure for robust design. Eng Optim 25:255–276

    Google Scholar 

  29. Schuëller GI, Jensen HA (2008) Computational methods in optimization considering uncertainties—an overview. Comput Methods Appl Mech Eng 198:2–13

    MATH  Google Scholar 

  30. Bhattacharjya S (2010) Robust optimization of structures under uncertainty, Ph.D. Thesis, Department of Civil Engineering. Bengal Engineering and Science University, Shibpur

    Google Scholar 

  31. Kleijnen JPC (1987) Statistical tools for simulation practitioners. Marcel Dekker Inc., New York

    MATH  Google Scholar 

  32. Jin R, Chen W, Simpson T (2001) Comparative studies of metamodeling techniques under multiple modeling criteria. Struct Multidiscip Optim 23:1–13

    Google Scholar 

  33. Sudret B (2012) Meta-models for structural reliability and uncertainty quantification. In: Proc. 5th Asian-Pacific Symp. Stuctural Reliab. Its Appl. (APSSRA, 2012), Singapore, pp 53–76

  34. Kim S-H, Na S-W (1997) Response surface method using vector projected sampling points. Struct Saf 19:3–19

    Google Scholar 

  35. Kang S-C, Koh H-M, Choo JF (2010) An efficient response surface method using moving least squares approximation for structural reliability analysis. Probabilistic Eng Mech 25:365–371

    Google Scholar 

  36. Jacquelin E, Adhikari S, Sinou J, Friswell MI (2014) Polynomial chaos expansion and steady-state response of a class of random dynamical systems. J Eng Mech 141:04014145

    Google Scholar 

  37. Rabitz H, Aliş ÖF (1999) General foundations of high-dimensional model representations. J Math Chem 25:197–233

    MathSciNet  MATH  Google Scholar 

  38. Kaymaz I (2005) Application of kriging method to structural reliability problems. Struct Saf 27:133–151

    Google Scholar 

  39. Deng J (2006) Structural reliability analysis for implicit performance function using radial basis function network. Int J Solids Struct 43:3255–3291

    MATH  Google Scholar 

  40. Mareš T, Janouchová E, Kučerová A (2016) Artificial neural networks in the calibration of nonlinear mechanical models. Adv Eng Softw 95:68–81

    Google Scholar 

  41. Richard B, Cremona C, Adelaide L (2012) A response surface method based on support vector machines trained with an adaptive experimental design. Struct Saf 39:14–21

    Google Scholar 

  42. Friedman JH (1991) Multivariate adaptive regression splines. Ann Stat 19:1–67

    MathSciNet  MATH  Google Scholar 

  43. Simpson T, Mauery T, Korte J, Mistree F (1998) Comparison of response surface and kriging models for multidisciplinary design optimization. In: 7th AIAA/USAF/NASA/ISSMO Symp. Multidiscip. Anal. Optim, St. Louis, MO, pp 381–391

  44. Giunta A, Watson L, Koehler J (1998) A comparison of approximation modeling techniques: polynomial versus interpolating models. In: Proc. Seventh AIAA/USAF/NASA/ISSMO Symp. Multidiscip. Anal. Optim. AIAA-98-4758. pp 1–13

  45. Ray T, Smith W (2006) A surrogate assisted parallel multiobjective evolutionary algorithm for robust engineering design. Eng Optim 38:997–1011

    Google Scholar 

  46. Chowdhury R, Rao BN, Prasad AM (2008) High dimensional model representation for piece-wise continuous function approximation. Commun Numer Methods Eng 24:1587–1609

    MathSciNet  MATH  Google Scholar 

  47. Chowdhury R, Rao BN, Prasad AM (2009) High-dimensional model representation for structural reliability analysis. Commun Numer Methods Eng 25:301–337

    MathSciNet  MATH  Google Scholar 

  48. Alis ÖF, Rabitz H (2001) Efficient implementation of high dimensional model representations. J Math Chem 29:127–142

    MathSciNet  MATH  Google Scholar 

  49. Chastaing G, Gamboa F, Prieur C (2011) Generalized hoeffding-sobol decomposition for dependent variables-application to sensitivity analysis. Electron J Stat 6:2420–2448

    MathSciNet  MATH  Google Scholar 

  50. Ho T-S, Rabitz H (2003) Reproducing kernel Hilbert space interpolation methods as a paradigm of high dimensional model representations: application to multidimensional potential energy surface construction. J Chem Phys 119:6433

    Google Scholar 

  51. Sobol IM (1993) Sensitivity estimates for nonlinear mathematical models. Math Model Comput Exp 1:407–414

    MathSciNet  MATH  Google Scholar 

  52. Wiener N (1938) The homogeneous Chaos. Am J Math 60:897. doi:10.2307/2371268

    MathSciNet  MATH  Google Scholar 

  53. Xiu D, Karniadakis GE (2002) The Wiener–Askey polynomial Chaos for stochastic differential equations. SIAM J Sci Comput 24:619–644

    MathSciNet  MATH  Google Scholar 

  54. Hampton J, Doostan A (2015) Coherence motivated sampling and convergence analysis of least squares polynomial chaos regression. Comput Methods Appl Mech Eng 290:73–97

    MathSciNet  MATH  Google Scholar 

  55. Filomeno Coelho R, Lebon J, Bouillard P (2011) Hierarchical stochastic metamodels based on moving least squares and polynomial chaos expansion. Struct Multidiscip Optim 43:707–729

    MathSciNet  MATH  Google Scholar 

  56. Madankan R, Singla P, Patra A, Bursik M, Dehn J, Jones M et al (2012) Polynomial chaos quadrature-based minimum variance approach for source parameters estimation. Procedia Comput Sci 9:1129–1138

    Google Scholar 

  57. Zheng Zhang TA, El-Moselhy IM, Elfadel L, Daniel (2014) Calculation of generalized polynomial-chaos basis functions and Gauss quadrature rules in hierarchical uncertainty quantification. IEEE Trans Comput Des Integr Circuits Syst 33:728–740

    Google Scholar 

  58. Zhao F, Tian Z (2012) Gear remaining useful life prediction using generalized polynomial chaos collocation method. In: Pham H (ed), Proc. 18TH ISSAT Int. Conf. Reliab. Qual. Des. pp 217–221

  59. Hosder S, Walters RW, Balch M (2012) Point-collocation nonintrusive polynomial chaos method for stochastic computational fluid dynamics. AIAA J 48:2721–2730

    Google Scholar 

  60. Blatman G, Sudret B (2010) An adaptive algorithm to build up sparse polynomial chaos expansions for stochastic finite element analysis. Probabilistic Eng Mech 25:183–197

    Google Scholar 

  61. Blatman G, Sudret B (2011) Adaptive sparse polynomial chaos expansion based on least angle regression. J Comput Phys 230:2345–2367

    MathSciNet  MATH  Google Scholar 

  62. Xiu D, Karniadakis GE (2002) Modeling uncertainty in steady state diffusion problems via generalized polynomial chaos. Comput Methods Appl Mech Eng 191:4927–4948

    MathSciNet  MATH  Google Scholar 

  63. Xiu D, Karniadakis GE (2003) Modeling uncertainty in flow simulations via generalized polynomial chaos. J Comput Phys 187:137–167

    MathSciNet  MATH  Google Scholar 

  64. Sudret B (2008) Global sensitivity analysis using polynomial chaos expansions. Reliab Eng Syst Saf 93:964–979

    Google Scholar 

  65. Pascual B, Adhikari S (2012) A reduced polynomial chaos expansion method for the stochastic finite element analysis. Sadhana-Acad Proc Eng Sci 37:319–340

    MathSciNet  MATH  Google Scholar 

  66. Pascual B, Adhikari S (2012) Combined parametric-nonparametric uncertainty quantification using random matrix theory and polynomial chaos expansion. Comput Struct 112:364–379

    Google Scholar 

  67. Craven P, Wahba G (1978) Smoothing noisy data with spline functions. Numer Math 31:377–403

    MathSciNet  MATH  Google Scholar 

  68. Sudjianto A, Juneja L, Agrawal H, Vora M (1998) Computer aided reliability and robustness assessment. Int J Reliab Qual Saf Eng 05:181–193

    Google Scholar 

  69. Wang X, Liu Y, Antonsson EK (1999) Fitting functions to data in high dimensionsal design space. In: ASME Des. Eng. Tech. Conf., Las Vegas, p DETC99/DAC-8622

  70. Krishnamurthy T (2003) Response surface approximation with augmented and compactly supported radial basis functions. In: 44th AIAA/ASME/ASCE/AHS/ASC Struct. Struct. Dyn. Mater. Conf., American Institute of Aeronautics and Astronautics, Reston, Virigina

    Google Scholar 

  71. Hardy RL (1971) Multiquadric equations of topography and other irregular surfaces. J Geophys Res 76:1905–1915

    Google Scholar 

  72. Buhmann MD (2000) Radial basis functions. Acta Numer 9:1–38

    MathSciNet  MATH  Google Scholar 

  73. Volpi S, Diez M, Gaul NJ, Song H, Iemma U, Choi KK et al (2015) Development and validation of a dynamic metamodel based on stochastic radial basis functions and uncertainty quantification. Struct Multidiscip Optim 51:347–368

    Google Scholar 

  74. Dai HZ, Zhao W, Wang W, Cao ZG (2011) An improved radial basis function network for structural reliability analysis. J Mech Sci Technol 25:2151–2159

    Google Scholar 

  75. Chau MQ, Han X, Jiang C, Bai YC, Tran TN, Truong VH (2014) An efficient PMA-based reliability analysis technique using radial basis function. Eng Comput 31:1098–1115

    Google Scholar 

  76. Chau MQ, Han X, Bai YC, Jiang C (2012) A structural reliability analysis method based on radial basis function. C Comput Mater Contin 27:128–142

    Google Scholar 

  77. Kriesel D (2010) A brief introduction to neural network

  78. Hagan MT, Demuth HB, Beale MH, Jesús OD (2008) Neural network design, 2nd edn. Cengage Learning, New Delhi

    Google Scholar 

  79. Shu S, Gong W (2016) An artificial neural network-based response surface method for reliability analyses of c-φ slopes with spatially variable soil, China. Ocean Eng 30:113–122

    Google Scholar 

  80. Dai H, Zhang H, Wang W (2015) A multiwavelet neural network-based response surface method for structural reliability analysis. Comput Civ Infrastruct Eng 30:151–162

    Google Scholar 

  81. Peng W, Zhang J, You L (2015) The hybrid uncertain neural network method for mechanical reliability analysis. Int J Aeronaut Sp Sci 16:510–519

    Google Scholar 

  82. Zio E (2006) A study of the bootstrap method for estimating the accuracy of artificial neural networks in predicting nuclear transient processes. IEEE Trans Nucl Sci 53:1460–1478

    Google Scholar 

  83. Vapnik VN (1998) Statistical learning theory. Wiley, New York

    MATH  Google Scholar 

  84. Goldstein H (1986) Classical mechanics. Addison-Wesley, Reading, MA

    MATH  Google Scholar 

  85. Z. Guo, G. Bai, Application of least qquares support vector machine for regression to reliability analysis. Chin J Aeronaut 22 (2009) 160–166

    Google Scholar 

  86. Lins ID, Droguett EL, das Chagas Moura M, Zio E, Jacinto CM (2015) Computing confidence and prediction intervals of industrial equipment degradation by bootstrapped support vector regression. Reliab Eng Syst Saf 137:120–128

    Google Scholar 

  87. Liu J, Vitelli V, Zio E, Seraoui R (2015) A novel dynamic-weighted probabilistic support vector regression-based ensemble for prognostics of time series fata. IEEE Trans Reliab 64:1203–1213

    Google Scholar 

  88. Gunn SR (1997) Support vector machines for classification and regression, Technical report, image speech and intelligent systems research group. Southampton, UK

  89. Xiao M, Gao L, Xiong H, Luo Z (2015) An efficient method for reliability analysis under epistemic uncertainty based on evidence theory and support vector regression. J Eng Des 26:340–364

    Google Scholar 

  90. Zhao W, Tao T, Zio E, Wang W (2016) A novel hybrid method of parameters tuning in support vector regression for reliability prediction: particle Swarm optimization combined With analytical selection. IEEE Trans Reliab 1–13

  91. Zhao W, Tao T, Zio E (2013) Parameters tuning in support vector regression for reliability forecasting. Chem Eng Trans 33:523–528

    Google Scholar 

  92. Coen T, Saeys W, Ramon H, De Baerdemaeker J (2006) Optimizing the tuning parameters of least squares support vector machines regression for NIR spectra. J Chemom 20:184–192

    Google Scholar 

  93. Olea RA (2011) Optimal contour mapping using Kriging. J Geophys Res 79:695–702

    Google Scholar 

  94. Warnes JJ (1986) A sensitivity analysis for universal kriging. Math Geol 18:653–676

    MathSciNet  Google Scholar 

  95. Krige DG (1951) A Statistical approach to some basic mine valuation problems on the witwatersrand. J Chem Metall Min Soc South Africa 52:119–139

    Google Scholar 

  96. Krige DG (1951) A statisitcal approach to some mine valuations and allied problems at the Witwatersrand. University of Witwatersrand

  97. Joseph VR, Hung Y, Sudjianto A (2008) Blind Kriging: a new method for developing metamodels. J Mech Des 130:031102

    Google Scholar 

  98. Hung Y (2011) Penalized blind kriging in computer experiments. Stat Sin 21:1171–1190

    MathSciNet  MATH  Google Scholar 

  99. Couckuyt I, Forrester A, Gorissen D, De Turck F, Dhaene T (2012) Blind Kriging: implementation and performance analysis. Adv Eng Softw 49:1–13

    Google Scholar 

  100. Kennedy M, O’Hagan A (2000) Predicting the output from a complex computer code when fast approximations are available. Biometrika 87:1–13

    MathSciNet  MATH  Google Scholar 

  101. Wang B, Bai J, Gea HC (2013) Stochastic Kriging for random simulation metamodeling with finite sampling. In: Vol. 3B 39th Des. Autom. Conf., ASME, p V03BT03A056. doi:10.1115/DETC2013-13361

  102. Qu H, Fu MC (2014) Gradient extrapolated Stochastic Kriging. ACM Trans Model Comput Simul 24:1–25

    MathSciNet  MATH  Google Scholar 

  103. Kamiński B (2015) A method for the updating of stochastic kriging metamodels. Eur J Oper Res 247:859–866

    MathSciNet  MATH  Google Scholar 

  104. Bhattacharyya B (2017) A critical appraisal of design of experiments for uncertainty quantification. Arch Comput Methods Eng. doi:10.1007/s11831-017-9211-x

    MATH  Google Scholar 

  105. Rivest M, Marcotte D (2012) Kriging groundwater solute concentrations using flow coordinates and nonstationary covariance functions. J Hydrol 472–473:238–253

    Google Scholar 

  106. Putter H, Young GA (2001) On the effect of covariance function estimation on the accuracy of Kriging predictors. Bernoulli 7:421–438

    MathSciNet  MATH  Google Scholar 

  107. Biscay Lirio R, Camejo DG, Loubes J-M, Muñiz Alvarez L (2013) Estimation of covariance functions by a fully data-driven model selection procedure and its application to Kriging spatial interpolation of real rainfall data. Stat Methods Appt 23:149–174

    MathSciNet  MATH  Google Scholar 

  108. Cleveland W (1979) Robust locally weighted regression and smoothing scatterplots. J Am Stat Assoc 74:829–836

    MathSciNet  MATH  Google Scholar 

  109. Hastie T, Loader C (1993) Local regression: automatic kernel carpentry (with discussion). Stat Sci 8:120–143

    Google Scholar 

  110. Fan J, Gijbels I (1992) Variable bandwidth and local linear regression smoothers. Ann Stat 20:196–216

    MathSciNet  MATH  Google Scholar 

  111. Cleveland W, Devlin S (1988) Locally weighted regression: an approach to regression analysis by local fitting. J Am Stat Assoc 83:596–610

    MATH  Google Scholar 

  112. Cleveland W, Devlin S, Grosse E (1988) Regression by local fitting. J Econom 37:87–114

    Google Scholar 

  113. M. Wand, M. Jones (1995) Kernel smoothing, CRC Press, Boca Raton, FL

    MATH  Google Scholar 

  114. Fan J, Gijbels I (1996) Local polynomial modelling and its applications, Chapman and Hall

  115. Schucany W (1995) Adaptive bandwidth choice for kernel regression. J Am Stat Assoc 90:535–540

    MathSciNet  MATH  Google Scholar 

  116. Fan J, Gijbels I (1995) Adaptive order polynomial fitting: bandwidth robustification and bias reduction. J Comput Graph Stat 4:213–227

    Google Scholar 

  117. Lall U, Moon Y, Kwon H, Bosworth K (2006) Locally weighted polynomial regression: parameter choice and application to forecasts of the Great Salt Lake. Water Resour Res 42

  118. Fan J (1993) Local linear regression smoothers and their minimax efficiencies. Ann Stat 21:196–216

    MathSciNet  MATH  Google Scholar 

  119. Fan J, Gasser T, Gijbels I, Brockmann M, Engel J (1997) Local polynomial regression: optimal kernels and asymptotic minimax efficiency. Ann Inst Stat Math 49:79–99

    MathSciNet  MATH  Google Scholar 

  120. Cheng M, Fan J, Marron J (1997) On automatic boundary corrections. Ann Stat 25:1691–1708

    MathSciNet  MATH  Google Scholar 

  121. Fan J, Marron J (1994) Fast implementations of nonparametric curve estimators, J Comput Graph Stat 3:35–56

    Google Scholar 

  122. Hall P, Wand M (1996) On the accuracy of binned kernel density estimators. J Multivar Anal 56:165–184

    MathSciNet  MATH  Google Scholar 

  123. Seifert B, Brockmann M, Engel J, Gasser T (1994) Fast algorithms for nonparametric curve estimation. J Comput Graph Stat 3:192–213

    MathSciNet  Google Scholar 

  124. Seifert B, Gasser T (2000) Data adaptive ridging in local polynomial regression. J Comput Graph Stat 9:338–360

    MathSciNet  Google Scholar 

  125. Li Q, Lu X, Ullah A (2003) Multivariate local polynomial regression for estimating average derivatives. J Nonparametr Stat 15:607–624

    MathSciNet  MATH  Google Scholar 

  126. Kai B, Li R, Zou H (2010) Local composite quantile regression smoothing: an efficient and safe alternative to local polynomial regression, J R Stat Soc Ser B-Stat Methodol 72:49–69

    MathSciNet  Google Scholar 

  127. McKay MD, Beckman RJ, Conover WJ (1979) A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 2:239–245

    MathSciNet  MATH  Google Scholar 

  128. Deb K (2001) Multi-objective optimization using evolutionary algorithms. Wiley, Chichester

    MATH  Google Scholar 

  129. Regis RG (2014) Evolutionary programming for high-dimensional constrained expensive black-box optimization using radial basis functions. IEEE Trans Evol Comput 18:326–347

    Google Scholar 

  130. Deb K, Gupta S, Daum D, Branke J, Mall AK, Padmanabhan D (2009) Reliability-Based Optimization Using Evolutionary Algorithms. IEEE Trans Evol Comput 13:1054–1074

    Google Scholar 

  131. DeLand S (2012) Solving large-scale optimization problems with MATLAB: A hydroelectric flow example

Download references

Acknowledgements

TC acknowledges the support of MHRD, Government of India and RC acknowledges the support of CSIR via Grant No. 22(0712)/16/EMR-II.

Author information

Authors and Affiliations

  1. Department of Civil Engineering, Indian Institute of Technology Roorkee, Roorkee, 247667, India

    Tanmoy Chatterjee & Rajib Chowdhury

  2. Department of Aerospace and Mechanical Engineering, University of Notre Dame, Notre Dame, IN, 46556, USA

    Souvik Chakraborty

Authors
  1. Tanmoy Chatterjee
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Souvik Chakraborty
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Rajib Chowdhury
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Tanmoy Chatterjee.

Ethics declarations

Conflict of interest

On behalf of all the authors, the corresponding author states that there is no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chatterjee, T., Chakraborty, S. & Chowdhury, R. A Critical Review of Surrogate Assisted Robust Design Optimization. Arch Computat Methods Eng 26, 245–274 (2019). https://doi.org/10.1007/s11831-017-9240-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11831-017-9240-5