Shape testing in varying coefficient models

Abstract

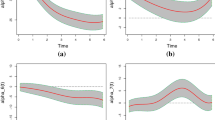
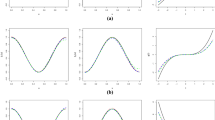
We consider varying coefficient models which are an extension of the classical linear regression models in the sense that the regression coefficients are replaced by functions in certain variables (often time). Varying coefficient models have been popular in longitudinal data and panel data studies, and have been applied in fields, such as finance and health sciences. We estimate the coefficient functions by splines. An important question in a varying coefficient model is whether a coefficient function is monotone or convex. We develop consistent testing procedures for monotonicity and convexity. Moreover, we provide procedures to test simultaneously the shapes of certain coefficient functions in a varying coefficient model. The tests use constrained and unconstrained regression splines. The performances of the proposed tests are illustrated on simulated data. We also give a real data application.

Appendices

Appendix A: Notation

In this paper, two submultiplicative matrix norms are considered. For a real matrix $\mathbf {A}\in \mathbb {R}^{n_1 \times n_2}$, $\Vert \mathbf {A}\Vert _2$ denotes the Frobenius norm: $\Vert \mathbf {A}\Vert _2=\sqrt{\sum _{i=1}^{n_1}\sum _{j=1}^{n_2}\mathbf {A}_{ij}^2}$. The norm $\Vert \cdot \Vert _\infty$ is defined by $\Vert \mathbf {A}\Vert _\infty =\max _{i=1,\ldots ,n_1}\sum _{j=1}^{n_2}|\mathbf {A}_{ij}|$. Furthermore, we use the notation

$$\begin{aligned} \mathbf {Y}_i= & {} (Y_{i1},\ldots ,Y_{iN_i})^\top \quad \mathbf {Y}=(\mathbf {Y}_{1},\ldots ,\mathbf {Y}_{n})^\top \\ \mathbf {B}(t)= & {} \left( \begin{array}{ccccccc} B_{01}(t;q_0) &{} \ldots &{} B_{0m_0}(t;q_0) &{} 0\ \ldots \ 0 &{} 0 &{} \ldots &{} 0 \\ 0 &{} \ldots &{} 0 &{} \ddots &{} 0 &{} \ldots &{} 0 \\ 0 &{} \ldots &{} 0 &{} 0\ \ldots \ 0 &{} B_{d1}(t;q_d) &{} \ldots &{} B_{dm_d}(t,q_d) \\ \end{array} \right) ,\\ \mathbf {B}(t)\in & {} \mathbb {R}^{d \times \mathrm{dim}} \quad \text{ where } \mathrm{dim}=\sum _{p=0}^dm_p \\ \mathbf {U}_{ij}^\top= & {} \mathbf {X}_{ij}^\top \mathbf {B}(t_{ij}) \in \mathbb {R}^{1 \times \mathrm{dim}} \quad \mathbf {U}_i=(\mathbf {U}_{i1},\ldots ,\mathbf {U}_{i N_i})^\top \in \mathbb {R}^{N_i \times \mathrm{dim}} \\ \mathbf {U}= & {} (\mathbf {U}_1,\ldots ,\mathbf {U}_n)^\top \in \mathbb {R}^{N\times \mathrm{dim}},\quad \text{ where } N=\sum _{i=1}^n N_i \\ \mathbf {W}_i= & {} {{\mathrm{diag}}}\Big (N_i^{-1},\ldots ,N_i^{-1}\Big ) \in \mathbb {R}^{N_i \times N_i}\quad (\text {a diagonal matrix with}\ N_i\ \text {times}\\&N_i^{-1}\ \text {on the diagonal})\\ \mathbf {W}= & {} {{\mathrm{diag}}}\Big (\mathbf {W}_1,\ldots , \mathbf {W}_n\Big ) \in \mathbb {R}^{N \times N}\quad (\text {a block diagonal matrix}\\&\text {with the matrices}\ \mathbf {W}_i\ \text {on the diagonal}) \\ \varvec{\varepsilon }_i= & {} (\varepsilon (t_{i1}),\ldots ,\varepsilon (t_{iN_i}))^\top \quad \varvec{\varepsilon }=(\varvec{\varepsilon }_1,\ldots ,\varvec{\varepsilon }_n)^\top \\ \mathbf {V}_i= & {} E(\varvec{\varepsilon }_i \varvec{\varepsilon }_i^\top ) \quad \mathbf {V}= E(\varvec{\varepsilon }\varvec{\varepsilon }^\top ). \end{aligned}$$

Appendix B: Assumptions

Assumptions:

• 1. The observation times $t_{ij},\ j = 1, \ldots , N_i,\ i = 1, \ldots , n,$ are chosen independently according to a distribution function $F_T(t)$ on $\mathcal {T}$. Moreover, they are independent of the response and the covariate process $\{(Y_i (t ),X_{i1}(t),\ldots , X_{id}(t))\},\ i = 1, \ldots , n$. The distribution function $F_T(t)$ has a Lebesgue density $f_T(t)$ that is bounded away from zero and infinity, uniformly over all $t \in \mathcal {T}$, that is, there exist positive constants $M_1$ and $M_2$, such that $M_1 \leqslant f_T (t)\leqslant M_2$ for all $t \in \mathcal {T}$.

• 2. The eigenvalues $\eta _0(t ), \ldots , \eta _d (t)$ of ${\varvec{\Sigma }}(t) = E(\mathbf {X}(t)\mathbf {X}(t)^\top )$ are bounded away from zero and infinity, uniformly over all $t \in \mathcal {T}$, that is, there exist positive constants $M_3$ and $M_4$, such that $M_3\leqslant \eta _0(t)\leqslant \ldots \leqslant \eta _d(t)\leqslant M_4$ for all $t \in \mathcal {T}$.

• 3. There exists a positive constant $M_5$, such that $|X_p(t)| \leqslant M_5$ for all $t \in \mathcal {T}$ and $p=0, \ldots ,d$.

• 4. There exists a positive constant $M_6$, such that $E(\varepsilon ^2(t))\leqslant M_6 < \infty$ for all $t \in \mathcal {T}$.

• 5. $\limsup _{n\rightarrow \infty }(\frac{ \max _p m_p}{\min _p m_p}) < \infty$.

• 6. The process $\varepsilon (t)$ can be decomposed as the sum of two independent stochastic processes, $\varepsilon ^{(1)}(t )$ and $\varepsilon ^{(2)}(t)$, where $\varepsilon ^{(1)}(t)$ is an arbitrary mean zero process and $\varepsilon ^{(2)}(t)$ is a process of measurement errors that are independent at different time points and have mean zero and constant variance $\sigma ^2$.