1 Introduction

Energy is one of world’s most important development preferences. Indeed, we notice that the international electricity requirement is rapidly rising accompanied by the shortage of fossil fuels. This makes its costs rapidly go up. Also, too much carbon dioxide (CO2) emissions in the atmosphere absorb heat and warming the planet because we burn fossil fuels like oil, natural gas and coal, for energy. Consequently, this leads to search for another solution to save earth and people life. This problem will be resolved if we choose alternative energy sources that prevent all these troubles. It should be a renewable source which can reliably generate as much energy as conventional fuels, and can do so without producing radioactive waste or carbon dioxide emissions[1, 2]. Moreover, renewable energy is abundant and constantly replenished. It includes energy from the sun and wind which are currently considered as the most important and profitable energy sources[3, 4].We concentrate on the solar energy because most renewable energy comes either directly or indirectly from the sun. The renewable solar energy can be provided by the sunlight intercepted by the earth that can be used to provide light, heat and generate electricity. It is a sustainable source that helps the world to get independence from the polluting energy sources and secures its own climate-friendly energy reserve. Photovoltaic models are constructed in order to catch solar energy but the main problem was how to optimize a photovoltaic system’s output under variable climatic conditions.

For this reason, a maximum power point tracking (MPPT) controller is being an indispensable tool. Indeed, several researchers have focused on the optimization problem of a photovoltaic power generation system and there are some propositions of a number of methods, such as perturb and observe (P&O) algorithm[5–7], the incremental conductance (IC) algorithm[8] that has problem of the high amplitude oscillations. There are other approaches based on the artificial intelligence method such as the fuzzy logic[9] and neural network methods[10] that need a database, but due to the uncertainties of climatic conditions, a robust controller seems to be very required to guarantee the tracking of optimal position with high accuracy. The sliding mode method[11–16] seems to be a suitable approach since it is characterized by a high precision and considerable robustness under internal and external perturbations for a non-linear system[17]. It is known that the first order sliding mode is a special and a robust control method. That is why we choose to work with this approach differently and use it for optimizing energy in a photovolatic (PV) system. In this paper, the proposed sliding mode control approach for MPPT is described in the first step. Then, a study of algorithm stability is presented. Finally, the implementation and results are presented in the last part. This method could be extended and applied for any kind of load connected to the PV array.

Notations.

  • G: Global irradiation (W/m2)

  • R s : Series resistance (Ω)

  • G n : Reference irradiation (W/m2)

  • R p : Parallel resistance (Ω)

  • T: Cell junction temperature (°C)

  • A: Ideality factor

  • T r : Reference cell temperature (° C)

  • Z: State variable

  • Iout: Output current (A)

  • α: Control signal

  • I ph : Photo-current (A)

  • Eg: Band gap energy (eV)

  • I rr : Saturation current (A) at Tref

  • q: Charge of an electron

  • I d : PV saturation current (A)

  • L: Inductance (H)

  • I scr : Short circuit current (A)

  • C: Capacitance (F)

  • Vout: Output voltage (V)

  • I pv : PV output current (A)

  • V vp : PV output voltage (V)

  • K i : Short circuit current temperature coefficient (A/°K)

  • Rload: Load resistance

  • K b : Boltzmann constant (1.38×10−23)

  • R pv = V pv /I pv :: PV resistance

  • ΔVoc: Short circuit voltage temperature coefficient

  • Vocs:: Open circuit voltage

  • P mpp :Optimal PV power

  • Nc: Number of PV cells

  • I mpp : Optimal PV current

  • V mpp : Optimal PV voltage

2 Photovoltaic characteristics

Photovoltaic is the direct conversion of light into electricity at the atomic level. When electromagnetic irradiations are exposed to a photovoltaic solar cell, we notice that electricity is produced in the form of a voltage. This phenomenon is called the photovoltaic effect that was first noted by a French physicist, Edmund Becquerel, in 1839. It takes place when a photon, which is the discrete bundle of light, affects the surface of the PV cell. Consequently, the electrons become excited. Because of the electrons ejection, a voltage is created. Therefore, to simplify the phenomena, we could say that the materiel of solar cell absorbs photons of light and release electrons. Then, electrodes related to the PV panel are used to collect the generated energy and manipulate it for some applications.

Diversified photovoltaic solar cell models have been suggested in the literature[18]. Fig. 1 presents a model of photovoltaic cell that is composed of a light generator source, diode, a resistor in parallel expressing a leakage current, and a series resistor describing an internal resistance to the current flow. The proposed photovoltaic model uses the mathematical expressions (1)–(3).

Fig. 1
figure 1

Model of a solar cell

Full size image

Equation (1) illustrates the current of the solar cell:

$${I_{pv}} = {I_{ph}} - {I_d}\left[ {{{\rm{e}}^{{{q{v_{pv}} + {I_{pv}}{R_s}} \over {{k_b}TA}}}} - 1} \right] - {{{V_{pv}} + {I_{pv}}{R_s}} \over {{R_p}}}.$$
(1)

The equation of the photo-current in terms of temperature and irradiation can be expressed as

$${I_{ph}} = {G \over {{G_n}}}[{I_{scr}} + {k_i}\left({T - {T_r}} \right)].$$
(2)

The saturation current I d is given by

$${I_d} = {{{I_{ph}} - {{{V_{ocs}} - \Delta {V_{oc}}({T_r} - T)} \over {{R_p}}}} \over {{{\rm{e}}^{{{q({V_{ocs}} - \Delta {V_{oc}}({T_r} - T))} \over {A{k_b}T}}}} - 1}}.$$
(3)

Parallel resistor R p was neglected because of its large resistance and the series resistor R s was neglected due to its very small resistance. In order to simplify the simulation, we adopt an approximate model so (1) will be replaced by

$${I_{pv}} = {I_{ph}} - {I_d}\left[ {{{\rm{e}}^{{{q{V_{pv}}} \over {{k_b}TA}}}} - 1} \right].$$
(4)

The equation of the photo-current will be the same but (3) will be replaced by

$${I_d} = {I_{rr}}{\left[ {{T \over {{T_r}}}} \right]^3}{{\rm{e}}^{{{q{E_g}} \over {{k_b}A}}\left[ {{1 \over {{T_r}}} - {1 \over T}} \right]}}.$$
(5)

As a first step, we will present the simulation results of a photovoltaic panel with the following values of irradiations mentioned in Fig. 2. We note that when the sun rises, the power grows, P-V curves shift to increasing values allowing the module to produce a higher electrical power under certain big value of irradiation. However, with different value of temperature as mentioned in Fig. 3, the PV generator’s power is decreasing with high value of temperature and causes a less marked decrease of the open circuit voltage.

Fig. 2
figure 2

Power-voltage characteristics with different irradiation values

Full size image
Fig. 3
figure 3

Power-voltage characteristics with different temperature values

Full size image

3 A boost converter model

For a photovoltaic system that is composed of a photovoltaic generator coupled with a resistive load, it requires to have a boost type converter. Its model is presented in Fig. 4 the direct current/direct current (DC/DC) boost converter will use an MPPT controller for the sake of maintaining the optimal output power. The corresponding system is described through a state equation with two sets that are depending on the switch state (SW). If it has a zero logic value (SW=0), the corresponding differential equation is given by

$$\left\{\matrix{{{\dot I}_{pv}} = {{{V_{pv}}} \over L} - {{{V_{{\rm{out}}}}} \over L} \hfill \cr{{\dot V}_{{\rm{out}}}} = {{{I_{pv}}} \over C} - {{{V_{{\rm{out}}}}} \over {C{R_{{\rm{load}}}}}}. \hfill \cr} \right.$$
(6)
Fig. 4
figure 4

Model of a boost converter

Full size image

If the SW has 1 logic value (SW=1), the differential equation is expressed as

$$\left\{{\matrix{{{{\dot I}_{pv}} = {{{V_{pv}}} \over L}} \hfill \cr{{{\dot V}_{{\rm{out}}}} = {{{V_{{\rm{out}}}}} \over {C{R_{{\rm{load}}}}}}.} \hfill \cr}} \right.$$
(7)

The dynamic equation for the boost converter can be illustrated by

$$\left\{{\matrix{{{{\dot I}_{pv}} = {{{V_{pv}}} \over L} - {{{V_{{\rm{out}}}}} \over L} + {{{V_{{\rm{out}}}}} \over L}\alpha} \cr{{{\dot V}_{{\rm{out}}}} = {{{I_{pv}}} \over C} - {{{V_{{\rm{out}}}}} \over {C{R_{{\rm{load}}}}}} - {{{I_{pv}}} \over C}\alpha .} \cr}} \right.$$
(8)

The model can be written in compact form as

$$\dot Z = (1 - \alpha){\dot Z_1} + \alpha {\dot Z_2}$$
(9)

where

$$\matrix{{\dot Z = {{\left[ {{{\dot I}_{pv}}\quad {{\dot V}_{{\rm{out}}}}} \right]}^{\rm{T}}}} \cr{{{\dot Z}_1} = {{\left[ {({{{V_{pv}}} \over L} - {{{V_{{\rm{out}}}}} \over L})\quad ({{{I_{pv}}} \over C} - {{{V_{{\rm{out}}}}} \over {C\;{R_{{\rm{load}}}}}})} \right]}^{\rm{T}}}} \cr{{{\dot Z}_2} = {{\left[ {({{{V_{pv}}} \over L})\quad (- {{{V_{{\rm{out}}}}} \over {C\;{R_{{\rm{load}}}}}})} \right]}^{\rm{T}}}.} \cr}$$

The general form of the nonlinear time invariant system of the proposed dynamic system is given as

$$\dot Z = \phi (Z) + \psi (Z).$$
(10)

4 The first order sliding mode approach for photovoltaic system

The first theoretical work on sliding regimes emerged in the early 1960s. Sliding mode control is known to be a robust control method appropriate for controlling switched systems. High robustness is maintained against various kinds of uncertainties, such as external disturbances and measurement error[19]. Generating a sliding regime can be summarized in two steps. The first step is the determination of the sliding surface S = 0. The second step allows finding a discontinuous signal input α(z, t) which leads the system trajectories to S = 0, from any initial condition Z(0) as shown in Fig. 5.

Fig. 5
figure 5

The sliding regime

Full size image

Let us start with the first step that is the selection of the stable hyper planes in the corresponding state where the movement should be restricted. This surface is invariant of the controlled dynamics, where the controlled dynamics are exponentially stable, and where the system tracks the desired set-point.

Define the sliding mode S(t) as

$$S(t) = \{z\backslash S(z,t) = 0\} .$$

.

For the photovoltaic system, the sliding surface will be selected as[20]

$${{\partial {P_{pv}}} \over {\partial {I_{pv}}}} = {I_{pv}}\left({{{\partial {V_{pv}}} \over {\partial {I_{pv}}}} + {{{V_{pv}}} \over {{I_{pv}}}}} \right) = 0.$$
(11)

The nontrivial solution of (9) is

$$\left({{{\partial {V_{pv}}} \over {\partial {I_{pv}}}} + {{{V_{pv}}} \over {{I_{pv}}}}} \right) = 0.$$
(12)

Thus, in the state space, a proper sliding manifold can be determined through

$$S(t,z) = {{\partial {V_{pv}}} \over {\partial {I_{pv}}}} + {{{V_{pv}}} \over {{I_{pv}}}}.$$
(13)

This surface expounds the rule for proper switching. When the trajectory state is away from the corresponding surface, a control law tries to return it and maintains its movement around the selected switching surface. The most important and serious mission is to conceive a control law that will drive the trajectory state to the sliding surface and maintain it on the surface this is the second step. To constrain the trajectories of the system presented by (8), we propose a first order sliding mode control to reach the performance and then to stay onto the sliding surface. Chosen according to the control objectives, the control law is presented as

((14))

A simple sliding mode control design can be written as

$$\alpha = {\alpha _{eq}} + {\alpha _d}$$
(15)

where α eq is called equivalent control. Note that, under the action of the equivalent control α eq , any trajectory starting from the manifold S(z) = 0 remains on it. Since Ṡ(z) = 0, α eq is given by

$$S[t,z] = \dot S(t,z) = 0.$$
(16)

This ensures the invariance of the sliding surface. The proposed discontinuous control α d guarantees a convergence in finite time onto the surface. It is defined as

$${\alpha _d} = M \times {\rm{sgn}}(S).$$
(17)

Equation (14) determines the equivalent control of our PV system. It takes the forms as

$$\dot S = {\left[ {{{\partial S} \over {\partial Z}}} \right]^{\rm{T}}},\quad \dot Z = {\left[ {{{\partial S} \over {\partial Z}}} \right]^{\rm{T}}},\quad (\phi (Z) + \psi (Z){\alpha _{eq}}) = 0.$$
(18)

Now, it is clear that the equivalent control will be defined as

$${\alpha _{eq}} = - {{{{\left[ {{{\partial S} \over {\partial Z}}} \right]}^{\rm{T}}}\phi (Z)} \over {{{\left[ {{{\partial S} \over {\partial Z}}} \right]}^{\rm{T}}}\psi (Z)}} = 1 - {{{V_{pv}}} \over {{V_{{\rm{out}}}}}}.$$
(19)

The real control signal is proposed as

((20))

5 Stability analysis

To conduct stability analysis for the corresponding control, it is common to use Lyapunov approach[14], which is adopted to identify this mission. This Lyapunov function must be defined from the sliding surface already selected. For sliding mode, the function V is generally defined by

$$V = {1 \over 2}{S^2}.$$
(21)

In this case, the sufficient condition is given by

$$\dot V = S\dot S < 0.$$
(22)

In this way, an asymptotic convergence to the surface S = 0 is guaranteed.

The derivative of the surface is calculated as

$$\matrix{{\dot S = {{\left[ {{{\partial S} \over {\partial Z}}} \right]}^{\rm{T}}} \times \dot Z =} \hfill \cr{\quad \left({3 \times {{\partial {R_{pv}}} \over {\partial {I_{pv}}}} + {I_{pv}} \times {{{\partial ^2}{R_{pv}}} \over {\partial I_{pv}^2}}} \right) \times \left({- {{{V_{{\rm{out}}}}} \over L}(1 - \alpha) + {{{V_{pv}}} \over L}} \right)} \hfill \cr}$$
(23)

where

$${{\partial {R_{pv}}} \over {\partial {I_{pv}}}} = {\partial \over {\partial {I_{pv}}}}\left[ {{{{V_{pv}}} \over {{I_{pv}}}}} \right] = {1 \over {{I_{pv}}}}{{\partial {V_{pv}}} \over {\partial {I_{pv}}}} - {{{V_{pv}}} \over {I_{pv}^2}}$$
(24)

and

$${{{\partial ^2}{R_{pv}}} \over {{\partial ^2}{I_{pv}}}} = {1 \over {{I_{pv}}}}{{{\partial ^2}{V_{pv}}} \over {I_{pv}^2}} - {2 \over {I_{pv}^2}}{{\partial {V_{pv}}} \over {\partial {I_{pv}}}} + {{2{V_{pv}}} \over {I_{pv}^3}}.$$
(25)

On the other hand, the PV voltage is needed to be expressed in terms of mathematical functions using the PV panel parameters as

$${V_{pv}} = {{{K_b}TA} \over q}\ln \left({{{{I_{ph}} + {I_d} - {I_{pv}}} \over {{I_d}}}} \right).$$
(26)

The first derivative of the voltage can be expressed by

$${{\partial {V_{pv}}} \over {\partial {I_{pv}}}} = {{{K_b}TA} \over q}{{{I_d}} \over {{I_{ph}} + {I_d} - {I_{pv}}}} < 0.$$
(27)

It is clear that the first derivative of the voltage has a negative sign. Turning now to the expression of the second derivative,

$${{\partial {V_{pv}}} \over {\partial {I_{pv}}}} = - {{{K_b}TA} \over q}{{{I_d}} \over {{{({I_{ph}} + {I_d} - {I_{pv}})}^2}}} < 0.$$
(28)

It is obvious from (26) that the second voltage derivative also has a negative sign. Moreover, the first derivative of the sliding surface can be presented as

$$\matrix{{\dot S = {{\left[ {{{\partial S} \over {\partial Z}}} \right]}^{\rm{T}}} \times \dot Z =} \cr{\left({3{{\partial {R_{pv}}} \over {\partial {I_{pv}}}} + {I_{pv}}{{{\partial ^2}{R_{pv}}} \over {\partial I_{pv}^2}}} \right) \times \left({- {{{V_{{\rm{out}}}}} \over L}\left({1 - \alpha} \right) + {{{V_{pv}}} \over L}} \right).} \cr}$$
(29)

Denote by A in the form of

$$A = {1 \over {{I_{pv}}}}{{\partial {V_{pv}}} \over {\partial {I_{pv}}}} - {{{V_{pv}}} \over {I_{pv}^2}} + {{{\partial ^2}{V_{pv}}} \over {\partial I_{pv}^2}}.$$
(30)

Thus,

$$\dot S = A \times \left({- {{{V_{{\rm{out}}}}} \over L}(1 - \alpha) + {{{V_{pv}}} \over L}} \right).$$
(31)

This term (30) has always a negative sign. It remains only to verify the stability condition for each state of the duty cycle α eq .

In order to verify the stability, we should ensure (20).

  • Case 1. If we consider that 0< α < 1, thus,

    $$\matrix{{\dot Z = - {{{V_{{\rm{out}}}}} \over L}(1 - \alpha) + {{{V_{pv}}} \over L} =} \hfill \cr{\quad \;\; - {{{V_{{\rm{out}}}}} \over L}(1 - {\alpha _{eq}} - {\alpha _d}) + {{{V_{pv}}} \over L} =} \hfill \cr{\quad \;\;{{{V_{{\rm{out}}}}} \over L}\left({1 - \left({1 - {{{V_{pv}}} \over {{V_{{\rm{out}}}}}}} \right) - {\alpha _d}} \right) + {{{V_{pv}}} \over L} =} \hfill \cr{\quad \;\;{{{V_{{\rm{out}}}}} \over L}{\alpha _d}.} \hfill \cr}$$
    (32)

    So, it is obvious that the derivative of the surface has been always opposite in sign to the surface S. Moreover,

    $$\dot S = A\dot Z = {A_{{\alpha _d}}} = AM \times {\rm{sgn}}(S) = N \times {\rm{sgn}}(S).$$
    (33)

    And N = AM is obviously considered as a negative quantity N < 0, so SṠ < 0.

  • Case 2. If α = 1, according to (18), this means that ((α eq + α d ) ≥ 1), so we have two cases to check according to the state of α eq :

    If α eq = 1, and according to (17), V pv = 0. For this case, the surface S is negative as it is explained in Fig. 6.

    So, if S < 0, we should decrease the control input. This means that (α eq + α d ) < 1.

    But this contradicts the case of α = 1 mentioned at the outset.

    If α eq < 1 and α eq + α d ≥ 1, we will have S > 0. We obtain SṠ < 0.

  • Case 3. If α = 0, (α eq + α d ≤ 0) and

    $$\dot Z = - {{{V_{{\rm{out}}}}} \over L} + {{{V_{pv}}} \over L} < 0.$$
    (34)
Fig. 6
figure 6

Evolution of control law according to the surface sign

Full size image

It is clear in this case that Ṡ > 0. As usual, there are two cases to check for the α eq :

If α eq = 0, this implies that

$${V_{{\rm{out}}}} = {V_{pv}}$$
(35)

It is as if the PV array is directly connected to the load. We are in the operating area where S > 0, so the duty cycle should increase in this case. But this contradicts our condition which is α = 0.

So for the case of α eq > 0 and α eq + α d ≤ 0, we obtain S < 0. Then the condition is checked. So in general, there must be a condition on the choice of the positive constant M. Moreover, to ensure the good operating of the controller, the constant M should not be selected too large, it must be kept at the minimum.

$$M \leq {1 \over {{{\left\vert {{\rm{sgn}}(s)} \right\vert}_{\max}}}}.$$
(36)

This case is presented when α eq = 0. This implies that

$$M\left\vert {{\rm{sgn}}(s)} \right\vert \leq 1.$$
(37)

More clearly,

$$M \leq {1 \over {\left\vert {{\rm{sgn}}(s)} \right\vert}}.$$
(38)

Then,

$$M \leq 1.$$
(39)

6 Simulation results

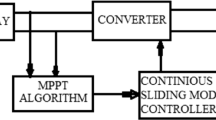
In this part, the PV system simulation is realized to research the effects of the sliding mode MPPT controller parameters on the system performance. The PV system presented by Fig. 7 is powered by a PV panel that has the following specifications mentioned in Table 1. Simulations are performed on a typical boost converter with L = 1.5 mH, C = 100 µF.

Fig. 7
figure 7

Photovoltaic system

Full size image
Table 1 System specification
Full size table

In the following, we will discuss reliability of the MPPT controller based on the first order sliding mode. So for the evaluation of the proposed MPPT controller performance, simulation results are presented in four subsections:

  1. 1)

    the reliability of the MPPT controller with changing irradiations,

  2. 2)

    the reliability of the MPPT controller with changing temperature,

  3. 3)

    the robustness of the MPPT controller against load variations,

  4. 4)

    the reliability of the MPPT controller with simultaneous change of irradiation and temperature.

Fig. 8 illustrates the climatic and load variations used in this simulation work. Indeed, we suppose that the irradiations trajectory mentioned in Fig. 8 (a) takes this form: it increases irradiation from 250 to 1000 W/m2 in steps of 250 units every 0.4 s then it decreases with the same decrement step using an abrupt change of illumination and we consider that the temperature is a constant (T = 25° C).

Fig. 8
figure 8

The climatic and load variations used in simulation work

Full size image

Under a constant irradiation value (G = 1000 W/m2), the temperature trajectory is supposed to be as mentioned in Fig. 8 (b) using the same abrupt change. This allows to test the reliability of the controller under a variable temperature that increases from 0° C to 100° C with an increment step equal to 25 units every 0.2 s and decreases using the same value for the decrement step.

The load variation illustrated in Fig. 8 (c) allows testing the robustness of the sliding mode controller against parametric changes. The load is changed from 25 to 50 Ω at t = 0.5 s, then it is changed to 100 Ω at t = 1 s, then it is decreased again to 50 Ω and finally returned to the initial resistance value.

The results of this climatic and load changes are indicated in Figs. 9–12. If we examine Fig. 9 that presents the power generated by the PV panel under different types of abrupt changes, we could remark that the power in Fig. 9 (a) is increasing with the high value of irradiations and decreasing if the irradiation is diminishing. We note that the MPPT controller offers a very rapid response against the irradiations change. So changing the light intensity incident on a solar cell changes all solar cell parameters, including the short-circuit current, the open-circuit voltage, and the efficiency. This is clear if we examine the power response.

Fig. 9
figure 9

PV power under climatic and load variations

Full size image
Fig. 10
figure 10

Control signal under climatic and load variations

Full size image
Fig. 11
figure 11

Iout under climatic and load variations

Full size image
Fig. 12
figure 12

Sliding surface under climatic and load variations

Full size image

The temperature factor can reduce efficiency and lower the solar panel’s energy output, the energy production efficiency of solar panels drops when the panel reaches hot temperatures as it is shown in Fig. 9 (b). So as we note the photovoltaic solar, panel power production works most efficiently in cold temperatures and this is clear via results. Under a load variation, we could see, as it is shown in Fig. 9 (c), that the sliding controller resists with success to the parametric changes and guarantees a stable optimal power. However, the oscillations are becoming significant when we decrease the load value.

So the proposed siding mode controller under variable environmental (irradiations and temperature) conditions and load variations is exhibiting an accurate control signal. This is clear if we examine Figs. 10 (a) and 10 (b), the sliding controller is adjusting in every case of the corresponding value of the control signal that extracts the maximum power from the PV panel. In Fig. 10 (c), the sliding mode controller is proving its robustness against load change.

Fig. 11 presents the load current response. It is meeting the requirement.

During the sliding regime, high frequency oscillations of the trajectory of the system around the sliding surface could result. This phenomenon is called chattering. It appears clearly in Fig. 12. At this level, the MPPT sliding mode ensures proper operation and considerable robustness.

Moreover, it shows low sensitivity against the fluctuation of the load. And according to the responses of power, control signal, load current and sliding surface, we can say that this is a robust control method.

A new test of robustness is proposed in this paper. It consists of a simultaneous change of irradiation and temperature as shown respectively in Figs. 13 and 14. More clearly, we suppose that the irradiation is moving from 1000 to 1200 W/m at t = 0.25 s and at the same time, the temperature is changing from 25°C to 45°C.

Fig. 13
figure 13

Temperature variation

Full size image
Fig. 14
figure 14

Irradiation variation

Full size image

Fig. 15 shows the PV power that is reaching its maximum value in every different climatic condition. Fig. 16 determines the control signal. The sliding MPPT ensures a high rapidity. Indeed, it takes 0.0003 s to find the second maximum power point. The PV system with the sliding controller has good dynamic and static performance.

Fig. 15
figure 15

Power under simultaneous climatic variation

Full size image
Fig. 16
figure 16

The control signal under simultaneous climatic variation

Full size image

7 Conclusions

An MPPT control scheme has been adopted to control a DC-DC boost converter. The MPPT control is based on the sliding mode approach. It is investigated to be a robust controller which can extract the maximum power under variable climatic and load conditions.

Simulation results give the proof that the first order sliding mode control system has robust characteristics and a fast transient response under irradiation, temperature and load-resistance variations. It responded well even under a sudden and instant two climatic factors change. In conclusion, the proposed first order sliding mode controller is suitable for optimizing and tracking the maximum power. It presents acceptable performance. It is important to approve its efficiency in real time which stills the main topic for next works. In order to propose a solution to the major problem of the sliding mode control which is mentioned in this paper, we could try to ameliorate the MPPT controller based on sliding mode by reducing the effect of chattering phenomena in order to get more adequate results. So as a future work, we plan to use a high order sliding mode controller for a PV system.