1 Introduction

Chaotic behavior has been observed in a variety of dynamical systems, and received intensive researches both theoretically and experimentally. A chaotic system is nonlinear, which exhibits sensitive, unpredictable and random-seeming behavior. Nevertheless, its state variables are bounded, and change with time in a deterministic manner. Chaos is considered to be a desirable phenomenon for use in potential applications to various fields, especially in secure communication. Investigation on application of chaos to cryptography was initiated by the work of synchronizing drive-response chaotic systems in [1], which has witnessed a rapid development in the recent years[2–4].

There are efficient schemes proposed for encrypting plaintext data for transmission through open channels. Typical additive chaotic masking generates the transmitted signal, by adding the chaotic signal to the plaintext at the transmitter as

$$s(t) = x(t) + p(t)$$
(1)

where x is the chaotic mask, p is the plaintext, and s is the information bearing signal to be transmitted. As s is obtained and the synchronization occurs on the receiver side, the plaintext p can be recovered by subtracting the synchronized signal from s. Chaotic modulation by multiplication is another useful masking method, described by

$$s(t) = x(t)p(t).$$
(2)

When the synchronization occurs on the receiver side, the plaintext p can be reconstructed by dividing the synchronized signal from s. Precautions have to be made for avoiding the possible singularity problem as the synchronized signal for x(t) may achieve zero at some time instants. Related modulation schemes are the chaotic parameter modulation[5, 6], which uses the signal to be encrypted to change the parameter of the chaotic transmitter.

In the aforementioned typical schemes, the inversion computing for decrypting is simple as they are linear in their arguments. The linearity nature leads to easy implementations of these schemes, but also allows ease of breaking. In the published literature, there exist efforts made for enhancing security. One way is to increase nonlinearity of the masking mechanism to be applied[7–8].It is observed that higher nonlinearity may lead to higher security. The major difficulty, however, lies in the inversion computing for decrypting.

Instead of the drive-response viewpoint, the concept of synchronization was further explored in [9] to link the classical notion of observers from control theory. This motivated attempts to apply such an observer-based synchronization methodology to chaotic communication. As a synchronization system is not available, parameter identification methods are alternative for chaotic communication[10], where parameter modulation is applied. Identification algorithms, with nice performance for tracking time-varying parameters, can be used to demodulate the signal of transmission.

In this paper, we shall formulate the problem of secure communication in terms of iterative learning[11–14]. An initial effort can be found in [15]. The learning algorithm is efficient for estimating time-varying parameters spanned over a finite time interval in a dynamical system. Nonlinear masking is adopted in our schemes and the difficulty in the inversion computing is avoided. The plaintext is assumed to be given over a pre-specified time interval. The learning algorithm uses only the transmitted signal s. Through learning, the plaintext can be recovered from the cipher-text. On the other hand, no synchronization occurs. The iterative learning method is related with the inversion system based approach[16–18]. However, our proposed learning algorithm is simple and does not need inversion computing. By comparing the proposed learning algorithm with the existing ones, it can been seen that 1) the unknowns to be estimated are not assumed to be slowly time varying, and 2) the learning algorithm ensures the consistency of estimates. In addition, a checkable convergence condition is given for the learning gain selection. The organization of the paper is as follows. For dealing with nonlinear masking, in Section 2, chaotic secure communication is formulated in terms of time-varying parameter identification problems, and the iterative learning methodology is shown to be applicable to solving such problems. Performance analysis for the proposed learning algorithm is given in Section 3. Two fundamental techniques are suggested for enhancing security of the iterative learning based communication in Section 4. Numerical results are presented in Section 5, and Section 6 draws the conclusions.

2 A secure communication system

Iterative learning offers an efficient tool for estimating time-varying unknowns in a dynamical system over a finite interval. The problem of chaotic secure communication is formulated based on this methodology of learning in this section.

2.1 Nonlinear masking

In our cryptographic scheme, the transmitter adopts a chaotic system of the form

$$\dot x = f(x,\alpha)$$
(3)

where x ∈ Rn is the state vector of the system, and α is the parameter chosen for the masking purpose, satisfying that αmin ≤ α ≤ αmax. The system could exhibit chaotic behavior as the parameter α varies within the region. A typical chaotic system is given in [19]. The nonlinear function ƒ is assumed to be smooth on Rn.

Let p(t) denote the plaintext to be transmitted, which is assumed to satisfy that αmin ≤ p(t) ≤ αmax. Here, we simply replace a with p(t) in (3) to obtain

$$\dot x = f(x,p).$$
(4)

The transmitted signal is constructed in the way of

$$s = g(x,p)$$
(5)

where x is the state given by (4). The nonlinear function g is chosen by designer such that s is bounded. The design of function g is an important procedure to enhance the degree of security. This will be clarified further in Section 4 and is justified in Section 5.

2.2 Iterative learning decryption

The duration of the plaintext p(t) is assumed to be finite, i.e., t ∈ [0, T] and T > 0 is finite. Given a tolerance error bound ϵ, the recovery objective on the receiver side is to find text p k (t),t ∈ [0, T] and k = 0, 1, 2, ⋯, where k indicates the iteration index, so that as iteration increases, the error between p k (t) and p(t) will be within the tolerance error bound, i.e., |p(t) − p k (t)| ≤ ϵ, t ∈ [0, T]. In this paper, we shall develop a learning algorithm to generate the texts p k (t), t ∈ [0, T]. p(t) can be recovered from the ciphertext via learning. Throughout this paper, let us denote by |a| the absolution value for a scalar a, and |a| = max1≤i≤n |a i | for an n-dimensional vector a = [a1, ⋯, a n ]T. The λ-norm for a time function b(t) is defined as |b|λ = supt∈[0, T]{e−λt|b(t)|},λ > 0.

The learning procedure is presented as follows:

Given the transmitted signal s(t), t ∈ [0, T], the initial estimate p0(t), t ∈ [0, T], the initial condition x0 and the tolerance error ε:

  1. 1)

    Set k = 0 and p k (t) = p0(t), t ∈ [0, T].

  2. 2)

    Put x k (0) = x0.

  3. 3)

    Obtain s k (t), t ∈ [0, T], by solving the following differential equations:

    $${\dot x_k} = f({x_k},{p_k})$$
    (6)
    $${s_k} = g({x_k},{p_k}).$$
    (7)
  4. 4)

    Calculate the error signal s(t) − sk(t), t ∈ [0, T].

  5. 5)

    Stop the procedure if |s(t) − sk(t) < ε, t ∈ [0, T], otherwise go to 6).

  6. 6)

    Produce p k +1(t), t ∈ [0, T], by using the update law

    $${p_k} = {\rm{sat}}({p_{k - 1}}) + \gamma (s - {s_k})$$
    (8)

    with learning gain γ to be designed.

  7. 7)

    Increase k by 1, k ⇐ k + 1, and goto 2) to repeat the procedure.

In (8), sat is the saturation function defined as, for a scalar b,

$$sat(b) = \left\{ {\begin{array}{*{20}c} {\bar b^1 ,if b < \bar b^1 } \\ {b,if \bar b^1 \leqslant b \leqslant \bar b^2 } \\ {\bar b^2 , if b > \bar b^2 } \\ \end{array} } \right.$$
(9)

where \(\bar b = \{{\bar b^1},{\bar b^2}\}\) represents the lower and upper bounds, satisfying that \({\bar b^1} < {\bar b^2}\). Case \({\bar b^1} \ne - {\bar b^2}\) indicates the asymmetric case. The saturation bounds are chosen appropriately such that the message signal p lies within them. The use of the saturation function aims to ensure the boundedness of p k .

As for (8), the closed-loop learning is suggested for exploiting the advantage of feedback. However, this method has the defect that the intrinsic time delay exists when obtaining sk, which would cause performance degradation due to the error between the actual signal and the estimated one. It will be shown that performance improvement can be made theoretically, provided that the estimation error is sufficiently small.

We emphasize the flexibility of choice for learning algorithms, and that the learning law (8) is by no means exclusive. Open-loop learning, using only the data from last cycle instead of the current cycle, can be applicable when one wants the message to be recovered off-line. A fully-saturated learning law is given as

$${p_{k + 1}}(t) = {\rm{sat}}(p_{k + 1}^{\ast}(t))$$
(10)
$$p_{k + 1}^{\ast}(t) = {\rm{sat}}(p_k^{\ast}(t)) + \gamma (s(t) - {s_k}(t)).$$
(11)

3 Performance analysis

Without any loss of generality, the state variables of the chaotic system undertaken are assumed to be bounded and there exists subset X ⊂ Rn such that x k (t) ∈ X for all t ∈ [0, T] and for all k. As the learning law that we apply is partially saturated, the boundedness of p k (t) is ensured as well. In order word, there exists subset P ⊂ R such that p k (t) ∈ P for all t ∈ [0, T] and for all k.

In practice, the signal s is acquired with the presence of measurement noise. In order to examine the effect of measurement noise, as well as the intrinsic time delay in obtaining s k , we consider the learning law in the form of

$${p_k} = {\rm{sat}}({p_{k - 1}}) + \gamma (s - {s_k}) + {\eta _k}$$
(12)

where η k indicates a variable related to measurement noise as in obtaining s, and the estimation error for s k . In addition, we rewrite the learning law (10) and (11) to be

$${p_{k + 1}}(t) = {\rm{sat}}(p_{k + 1}^{\ast}(t))$$
(13)
$$p_{k + 1}^{\ast}(t) = {\rm{sat}}(p_k^{\ast}(t)) + \gamma (s(t) - {s_k}(t)) + {\eta _k}.$$
(14)

The initial condition is usually used as a security key in the conventional chaotic secure communication systems. It is expected that any initial condition error will result in failing to decrypt the confidential information. We shall also examine the effect of the initial condition error on performance of the proposed method.

To make the problem more feasible, the following assumptions are imposed.

  • Assumption 1. x k 0) is set to x0+ϵ0 at the beginning of each cycle, where ϵ0 is the initial condition error satisfying

    $$\vert {x_0} - {x_k}(0)\vert = {\epsilon _0}.$$

  • Assumption 2. η k is assumed to satisfy

    $$\vert {\eta _k}\vert \leq {\epsilon _\eta}$$

    where ϵ η > 0.

  • Assumption 3. \({g_p}(x,p)(= {{\partial g(x,p)} \over {\partial p}} \ne 0\) for all x ∈ X and for all p ∈ P.

  • Assumption 4. ƒ (x, p) is local Lipschitz in both x and p, i.e., there exists lƒ > 0 such that

    $$\vert f(x^{\prime},p^{\prime}) - f(x^{\prime\prime},p^{\prime\prime})\vert \leq {l_f}(\vert x^{\prime} - x^{\prime\prime}\vert + \vert p^{\prime} - p^{\prime\prime}\vert)$$

    for any x′, x″ ⌈ X and for any p′, p″ ∈ P.

  • Assumption 5. g(x, p) is local Lipschitz in both x and p, i.e., there exists l g > 0 such that

    $$\vert g(x^{\prime},p^{\prime}) - g(x^{\prime\prime},p^{\prime\prime})\vert \leq {l_g}(\vert x^{\prime} - x^{\prime\prime}\vert + \vert p^{\prime} - p^{\prime\prime}\vert)$$

    for any x′, x″ ∈ X and for any p′, p″ ∈ P.

Under Assumption 1, the initial condition of the receiver is set to x0 + ϵ0, while the initial condition of the transmitter is set to x0. The convergence result of the iterative learning based secure communication system is stated in the following theorem.

With the aid of the following lemma (see Appendix A for the proof), we can establish the convergence of the partially-saturated learning algorithm.

  • Lemma 1. For real numbers a and b, if \({\bar b^1} < a < {\bar b^2}\), then

    $$\vert a - {\rm{sat}}(b){\vert ^r} \leq \vert a - b{\vert ^r}$$
    (15)

    where r > 0 is a given real number.

  • Theorem 1. Consider the system consisting of the transmitters (4) and (5), and the receivers (6) and (7), satisfying Assumptions 1–5. Let the learning law (12) be applied with the learning gain chosen to satisfy, for all x k ∈ X and for all \({\bar p_k} \in P\),

    $$\left\vert {{1 \over {1 + \gamma {g_p}({x_k},{{\bar p}_k})}}} \right\vert \leq \rho < 1.$$
    (16)

    Then,

    $$\mathop {\lim}\limits_{k \rightarrow \infty} \;\sup \vert p - {p_k}{\vert _\lambda} \leq {{\bar \epsilon} \over {1 - \bar \rho}}$$

    with \(\bar \epsilon,\bar \rho\) and \({\bar p_k}\) are to be specified.

  • Proof. See Appendix B. □

The robustness property of the learning algorithm, given in Theorem 1, is particularly desirable due to its iterative nature. This property ensures the boundedness of the error p−p k , and the achieved error bound depends on the bounds of measurement noise and initial condition error. The robustness result fully characterizes the effect of measurement noise and initial condition error, implying that the recovery of the message will not be easy if the signal to noise ratio is not designed appropriately, or the initial condition is not known exactly.

The convergence result in the absence of uncertainties is presented in Corollary 1.

  • Corollary 1. Let the system, consisting of the transmitters (4) and (5), and the receivers (6) and (7), satisfy Assumptions 1–5. The learning law (12) is applied with the learning gain chosen to satisfy (16). Then, the error p(t) −p k (t) converges to zero on [0, T] uniformly as k → ∞, when ϵ0 = 0 and ϵ η = 0.

  • Proof. The proof is straightforward by that for Theorem 1. □

By Corollary 1, the zero-error convergence over the entire interval can be guaranteed in the absence of the uncertainties. This implies that exact decryption over the entire interval [0, T] is achieved. We would like to note that the proposed method yields such complete recovery of message, whereas the message recovery by most existing methods is in an asymptotic manner. The complete recovery through learning is useful to enhance the security by designating the starting time of the message in the transmitted signal.

For the open-loop learning, we have the following robustness and convergence results.

  • Theorem 2. Consider the system consisting of the transmitters (4) and (5), and the receivers (6) and (7), satisfying Assumptions 1–5. Let the learning laws (13) and (14) be applied with the learning gain chosen to satisfy, for all x k ∈ X and for all \({\bar p_k} \in P\),

    $$\vert 1 - \gamma {g_p}({x_k},{\bar p_k})\vert \leq \rho < 1.$$
    (17)

    Then, lim sup

    $$\mathop {\lim \sup}\limits_{k \rightarrow \infty} \vert p - {p_k}{\vert _\lambda} \leq {{\bar \epsilon} \over {1 - \bar \rho}}$$

    with \(\bar \epsilon,\bar \rho\), and \({\bar p_k}\) are to be specified.

  • Proof. See Appendix C. □

4 Security enhancements

Two fundamental techniques, in this section, are suggested for enhancing security of the iterative learning based communication scheme presented in Section 2. Here, the results are presented for the closed-loop learning. However, the proposed techniques are also applicable when the open-loop learning algorithm is used.

The first one also generates the signal s in the manner specified by (5). However, instead of the directly replacing α with p(t) in the chaotic system, the transmitted signal is taken to replace the parameter as

$$\dot x = f(x,s).$$
(18)

The system is assumed to be of chaotic behavior within the region S to which s belongs. On the side of receiver, s k (t),t ∈ [0, T], is obtained by solving the differential equations as

$${\dot x_k} = f({x_k},{s_k}).$$
(19)

  • Assumption 4′. ƒ (x, s) is local Lipschitz in both x and s, i.e., there exists l f > 0 such that

    $$\vert f(x^{\prime},s^{\prime}) - f(x^{\prime\prime},s^{\prime\prime})\vert \leq {l_f}(\vert x^{\prime} - x^{\prime\prime}\vert + \vert s^{\prime} - s^{\prime\prime}\vert)$$

    for all x ∈ X and for all s ∈ S.

  • Theorem 3. Consider the system consisting of the transmitters (5) and (18), and the receivers (7) and (19), satisfying Assumptions 1–3, 4’ and 5. Let the update law (12) be applied with the learning gain chosen to satisfy (16). Then, the same results as in Theorem 1 are obtained.

  • Proof. Integrating both sides of (18) and (19) gives rise to

    $$x(t) - {x_k}(t) \leq x(0) - {x_k}(0) - \int_0^t {(f(x,s) - s({x_k},{s_k})){\rm{d}}\tau .}$$

    By Assumptions 1, 4’ and 5, we have

    $$\matrix{{\vert x(t) - {x_k}(t)\vert \leq} \hfill \cr{\quad \vert x(0) - {x_k}(0)\vert + \int_0^t {{l_f}(\vert x - {x_k}\vert + \vert s - {s_k}\vert)} {\rm{d}}\tau} \hfill \cr{\quad \vert x(0) - {x_k}(0)\vert + \int_0^t {{l_f}(\vert x - {x_k}\vert + {l_g}(x - {x_k} +}} \hfill \cr{\quad \vert p - {p_k}\vert)){\rm{d}}\tau =} \hfill \cr{\quad {\epsilon _0} + \int_0^t {{l_f}((1 + {l_g})\vert x - {x_k}\vert + {l_g}\vert p - {p_k}\vert){\rm{d}}\tau .}} \hfill \cr}$$

    Using Bellman-Gronwall Lemma yields

    $$\matrix{{\vert x(t) - {x_k}(t)\vert \leq} \hfill \cr{\quad {\epsilon _0}{{\rm{e}}^{{l_f}(1 + {l_g})t}} + {l_f}{l_g}\int_0^t {{{\rm{e}}^{{l_f}(1 + {l_g})(t - \tau)}}} \vert p - {p_k}\vert {\rm{d}}t.} \hfill \cr}$$
    (20)

    Using the same derivations to arrive at (B3) in Appendix, we obtain

    $$\left| {p - p_k } \right| \leqslant \rho \left( {\left| {p - p_{k - 1} } \right| + l_g \left| \gamma \right|\left| {x - x_k } \right| + \varepsilon _\eta } \right).$$
    ((21))

    Substituting (20) into (21) results in

    $$\matrix{{\vert p - {p_k}\vert - \rho {l_f}l_g^2\vert \gamma \vert \int_0^t {{{\rm{e}}^{{l_f}(1 + {l_g})(t - \tau)}}} \vert p - {p_k}\vert {\rm{d}}\tau \leq} \hfill \cr{\quad \rho (\vert p - {p_{k - 1}}\vert + {l_g}\vert \gamma \vert {\epsilon _0}{{\rm{e}}^{{l_f}(1 + {l_g})t}} + {\epsilon _\eta}).} \hfill \cr}$$

    As λ > l f (1 + l g ), we have

    $$\matrix{{\left({1 - \rho {l_f}l_g^2\vert \gamma \vert {{1 - {{\rm{e}}^{({l_f}(1 + {l_g}) - \lambda)T}}} \over {\lambda - {l_f}(1 + {l_g})}}} \right)\vert p - {p_k}{\vert _\lambda} \leq} \hfill \cr{\rho (\vert p - {p_{k - 1}}{\vert _\lambda} + {l_g}\vert \gamma \vert {\epsilon _0} + {\epsilon _\eta}).} \hfill \cr}$$
    (22)

    Let us define

    $$\matrix{{\bar \rho = {\rho \over {1 - \rho {l_f}l_g^2\vert \gamma \vert {{1 - {{\rm{e}}^{({l_f}(1 + {l_g}) - \lambda)T}}} \over {\lambda - {l_f}(1 + {l_g})}}}}} \hfill \cr{\bar \epsilon = \bar \rho ({l_g}\vert \gamma \vert {\epsilon _0} + {\epsilon _\eta}).} \hfill \cr}$$

    Equation (22) becomes

    $$\vert p - {p_k}{\vert _\lambda} \leq \bar \rho \vert p - {p_{k - 1}}{\vert _\lambda} + \bar \epsilon .$$

Since 0 ≤ ρ < 1, it is possible to choose a sufficiently large λ(>lƒ) such that

$$1 - \rho {l_f}l_g^2\vert \gamma \vert {{1 - {{\rm{e}}^{({l_f}(1 + {l_g}) - \lambda)T}}} \over {\lambda - {l_f}(1 + {l_g})}} > 0$$

and \(0 \le \bar \rho < 1\). Therefore, we obtain a contraction mapping in |p − p k |λ and the error will reduce to the bound \({{\bar \epsilon} \over {1 - \bar \rho}}\) in the limit. □

One more masking technique is to enhance nonlinearity of the mechanism for generating the signal s, for which we shall use a composite function, formed by the composition of one function on another, i.e.,

$$\matrix{{s = g(x,{s^1})} \hfill \cr{{s^1} = h(x,p).} \hfill \cr}$$
(23)

On the side of receiver, we use the following for encrypting

$$\matrix{{{s_k} = g({x_k},s_k^1)} \hfill \cr{s_k^1 = h({x_k},{p_k}).} \hfill \cr}$$
(24)

The chaotic system for the masking scheme is the same as (4).

  • Assumption 5′. g(x, s) is local Lipschitz in both x and s, i.e., there exists l g > 0 such that

    $$\vert g(x^{\prime},s^{\prime}) - g(x^{\prime\prime},s^{\prime\prime})\vert \leq {l_g}(\vert x^{\prime} - x^{\prime\prime}\vert + \vert s^{\prime} - s^{\prime\prime}\vert)$$

    for all x v X and for all s ∈ S.

  • Assumption 6. h(x, p) is local Lipschitz in both x and p, i.e., there exists l h > 0 such that

    $$\vert h(x^{\prime},p^{\prime}) - h(x^{\prime\prime},p^{\prime\prime})\vert \leq {l_h}(\vert x^{\prime} - x^{\prime\prime}\vert + \vert p^{\prime} - p^{\prime\prime}\vert)$$

    for all x ∈ X and for all p ∈ P.

It follows from the update law (12) that

$$\matrix{{p - {p_k} = p - {\rm{sat}}({p_{k - 1}}) -} \hfill \cr{\quad \gamma [g(x,h(x,p)) - g({x_k},h({x_k},{p_k}))] - {\eta _k}.} \hfill \cr}$$

By resorting the mean value theorem, \(g({x_k},h({x_k},p)) - g({x_k},h({x_k},{p_k})) = {g_h}{h_p}({x_k},{\bar p_k})(p - {p_k}),\quad {\bar p_k} = p + (1 - \xi)({p_k} - p),\,0 < \xi < 1\), we obtain

$$\matrix{{(1 + \gamma {g_h}{h_p}({x_k},{{\bar p}_k}))(p - {p_k}) =} \hfill \cr{\quad p - {\rm{sat}}({p_{k - 1}}) - \gamma [g(x,h(x,p)) - g({x_k},h({x_k},p))] - {\eta _k}.} \hfill \cr}$$

Taking absolute values on both sides of the above equation, we have

$$\matrix{{\vert p - {p_k}\vert \leq} \hfill \cr{\quad \vert 1 + \gamma {g_h}{h_p}({x_k},{{\bar p}_k}){]^{- 1}}\vert [\vert p - {\rm{sat}}({p_{k - 1}})\vert +} \hfill \cr{\quad \vert \gamma \vert \vert g(x,h(x,p)) - g({x_k},h({x_k},p))\vert + \vert {\eta _k}\vert ].} \hfill \cr}$$

Let γ be chosen such that

$$\left\vert {{1 \over {1 + \gamma {g_h}{h_p}({x_k},{{\bar p}_k})}}} \right\vert \leq \rho < 1$$
(25)

for all x k ∈ X and for all \({\bar p_k} \in P\). Then,

$$\matrix{{\vert p - {p_k}\vert \leq} \hfill \cr{\quad \rho (\vert p - {p_{k - 1}}\vert + {l_g}(1 + {l_h})\vert \gamma \vert \vert x - {x_k}\vert + {\epsilon _\eta}).} \hfill \cr}$$
(26)

Note that the following equality holds.

$$\vert x(t) - {x_k}(t)\vert \leq {\epsilon _0}{{\rm{e}}^{{l_f}t}} + {l_f}\int_0^t {{{\rm{e}}^{{l_f}(t - \tau)}}} \vert p - {p_k}\vert {\rm{d}}\tau .$$
(27)

Substituting (27) into (26) yields

$$\matrix{{\vert p - {p_k}\vert - \rho {l_f}{l_g}(1 + {l_h})\vert \gamma \vert \int_0^t {{{\rm{e}}^{{l_f}(t - \tau)}}} \vert p - {p_k}\vert {\rm{d}}\tau \leq} \hfill \cr{\quad \rho (\vert p - {p_{k - 1}}\vert + {l_g}(1 + {l_h})\vert \gamma \vert {\epsilon _0}{{\rm{e}}^{{l_f}t}} + {\epsilon _\eta}).} \hfill \cr}$$

As λ > l f , we obtain

$$\matrix{{(1 - \rho {l_f}{l_g}(1 + {l_h})\vert \gamma \vert {{1 - {{\rm{e}}^{({l_f} - \lambda)T}}} \over {\lambda - {l_f}}})\vert p - {p_k}{\vert _\lambda} \leq} \hfill \cr{\quad \rho (\vert p - {p_{k - 1}}{\vert _\lambda} + {l_g}(1 + {l_h})\vert \gamma \vert {\epsilon _0} + {\epsilon _\eta}).} \hfill \cr}$$
(28)

Let us define

$$\matrix{{\bar \rho = {\rho \over {1 - \rho {l_f}{l_g}(1 + {l_h})\vert \gamma \vert {{1 - {{\rm{e}}^{({l_f} - \lambda)T}}} \over {\lambda - {l_f}}}}}} \hfill \cr{\bar \epsilon = \bar \rho ({l_g}(1 + {l_h})\vert \gamma \vert {\epsilon _0} + {\epsilon _\eta}).} \hfill \cr}$$

Equation (28) becomes

$$\vert p - {p_k}{\vert _\lambda} \leq \bar \rho \vert p - {p_{k - 1}}{\vert _\lambda} + \bar \epsilon .$$

We are now at a position to summary the robustness and convergence result.

  • Theorem 4. Consider the system consisting of the transmitters (4) and (23), and the receivers (6) and (24), satisfying Assumptions 1–4, 5′ and 6. Let update law (12) be applied with the learning gain chosen to satisfy (25). Then, the same results as in Theorem 1 are obtained.

The scheme given by (23) and (24) just uses the composition of two nonlinear functions. For security enhancement, however, multiple composite functions can be applied in the form of

$$\left\{{\matrix{{s = g(x,{s^1})} \hfill \cr{{s^1} = {h_1}(x,{s^2})} \hfill \cr{\quad \quad \cdots} \hfill \cr{{s^{m - 1}} = {h_{m - 1}}(x,{s^m})} \hfill \cr{{s^m} = {h_m}(x,p).} \hfill \cr}} \right.$$
(29)

The theoretical analysis for the case of multiple composition follows the similar lines to the derivations for Theorem 4, where the nonlinear functions used for composition are required to be Lipschitz in their arguments. It should be to noted that the composite function is Lipschitz as the functions used to form the composition are Lipschitz in their arguments.

5 Case studies

Consider the following unified chaotic system proposed in [19],

$$\matrix{{{{\dot x}_1} = (25\alpha + 10)({x_2} - {x_1})} \hfill \cr{{{\dot x}_2} = (28 - 35\alpha){x_1} - {x_1}{x_3} + (29\alpha - 1){x_2}} \hfill \cr{{{\dot x}_3} = {x_1}{x_2} - {{\alpha + 8} \over 3}{x_3}.} \hfill \cr}$$

The message masking is carried out by calculating with the nonlinear function as

$$s = {1 \over {2\tanh (\varrho (x,p)) + 1}}$$
(30)
$$\varrho (x,p) = {c_1}{x_3} + ({c_2}{x_1} + {x_3})p$$
(31)

where p indicates the plaintext, and C i , i = 1, 2, 3, are adjustable parameters.

In the chaotic system, we replace α with p, and the system becomes

$$\matrix{{{{\dot x}_1} = (25p + 10)({x_2} - {x_1})} \hfill \cr{\dot x = (28 - 35p){x_1} - {x_1}{x_3} + (29p - 1){x_2}} \hfill \cr{{{\dot x}_3} = {x_1}{x_2} - {{p + 8} \over 3}{x_3}.} \hfill \cr}$$

For the learning law (12), it is easy to choose the learning gain according to the convergence condition (16).

$${{\partial g} \over {\partial p}} = {1 \over 2}{\rm{sec}}{{\rm{h}}^{\rm{2}}}(\varrho (x,p))({c_2}{x_1} + {c_3}).$$

Due to the boundedness of the function sech, it is easy for us to choose γ. In view of (16), we have to choose c2 and c3 such that c2x1 + c3 > 0.

We shall test the iterative learning based secure communication scheme for the settings as

$$\matrix{{{x^0} = {{[10,20,30]}^{\rm{T}}}} \hfill \cr{{c_1} = {1 \over {100}},{c_2} = {1 \over {100}},{c_3} = 1} \hfill \cr{{m_{\min}} = 0.4,{m_{\max}} = 0.9.} \hfill \cr}$$

Our scheme does not need the message to be differentiable, which can be discontinuous ones tailored for digital communication.

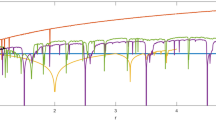
The plaintext is chosen to be a square wave on the interval [0, 6], i.e., T = 6. The transmitted signal is generated by (30), which is shown in Fig. 1. Note that our scheme does not need the knowledge about x1(t),x2(t),x3(t),t ∈ (0,T]. In order to recovery the message from the transmitted signal, the learning law (12) is applied with the setting of P0(t)=0, t ∈ [0,T]. Define the performance index as \({J_k} = {\sup _{t \in [0,T]}}|p(t) - {p_k}(t)|\). Fig. 2 shows the convergence rate comparison with different learning gains of γ = 0.5, 1.5 and 3. It verifies that a larger learning gain could lead to a faster convergence rate. With the choice of γ =3, the performance of J k < 10−5 is achieved at the cycle k = 15. The recovered message is shown in Fig. 3.

Fig. 1
figure 1

The transmitted signal generated by (30)

Full size image
Fig. 2
figure 2

Convergence rate comparison with different learning gains

Full size image
Fig. 3
figure 3

Message recovery

Full size image

The robustness of a learning algorithm is crucial due to its iteration nature. We then examine the robustness of the scheme to initial condition error and measurement noise. Let us set the initial condition to be \({x^0} + {1 \over {10}}{[1, - 1,1]^{\rm{T}}}\), where x0 is set to be the same as that in generating the transmitted signal, \({\eta _k} = {1 \over {1000}} \times (2{\rm{rand - 1)}}\), and the rand is a random scalar, chosen from a uniform distribution on the interval (0, 1). The recovery result obtained through 100 iterations is shown in Fig. 4. It is observed from Fig. 4 that our learning scheme will not be divergent in the presence of the uncertainties, but robust to the uncertainties.

Fig. 4
figure 4

Robustness to presence of initial condition error and measurement error

Full size image

The recovery performance with the proposed techniques for enhancing security is now examined. Let us replace the parameter α with the signal s, instead of the message signal p. Other settings remain the same. The numerical results are shown in Figs. 5 and 6. Fig. 5 depicts the convergence rate comparison with different learning gains. The performance of J k < 10−5 is achieved at the cycle k =20 as we choose γ = 3. Robustness of the scheme to initial condition error and measurement noise is examined in Fig. 6.

Fig. 5
figure 5

Convergence rate comparison. The parameter α is replaced by the signal s

Full size image
Fig. 6
figure 6

Robustness to presence of initial condition error and measurement error. The parameter a is replaced by the signal s

Full size image

The following composite function is then used to generate the signal s as

$$s = {1 \over {2(\tanh (\varrho (x,{s^1})) + 1)}}$$
(32)
$${s^1} = {1 \over {2(\tanh (\varrho (x,p)) + 1)}}$$
(33)

while other settings remain the same. The simulation results are shown in Figs. 7 and 8. The convergence rate comparison with different learning gains of γ = 2, 4 and 6 is given in Fig. 7. J k < 10−5 is achieved at the cycle k = 159 as γ = 6 is chosen. It is clarified that more iterations are needed to achieve the same performance as high nonlinearity is included. Fig. 8 shows the robustness of the scheme to initial condition error and measurement noise.

Fig. 7
figure 7

Convergence rate comparison. The transmitted signal is generated by (32)

Full size image
Fig. 8
figure 8

Robustness to presence of initial condition error and measurement error. The transmitted signal is generated by (32)

Full size image

6 Conclusions

The iterative learning perspective on secure communication is presented, in this paper, allowing us to apply a nonlinear mechanism for masking without inversion computing for decryption. In addition, the masking can be applied jointly with parameter modulation. The convergence condition of the learning algorithm has been derived, by which the learning gain can be chosen. The technique by increasing nonlinearities in masking is presented for enhancing security, and the learning algorithm has been shown to work well. The computer simulation has been carried out and numerical results have been provided to show the effectiveness and feasibility of the developed method.