Introduction

As an integral part of ecosystems, lakes undergo dynamic transformations—both qualitative (chemical composition) and quantitative (water level, resource fluctuations and changes in lake shape)—over the course of their existence. The most dynamic among these parameters, water-level fluctuations (WLFs), affect physical and morphometric transformations [e.g. sedimentation (Håkanson 1977), biogeochemical alterations (Furey et al. 2004) and changes in lacustrine ecosystem dynamics (Coops et al. 2003)], with attending shifts in flora and fauna. WLF also has effects on light penetration (Loiselle et al. 2005) and water temperature (Nowlin et al. 2004). In addition to being important for water resources management, the ability to accurately forecast changes in lacustrine water levels also has economic [e.g. energy generation (Walton 2010), fisheries (Marshall and Maes 1995), tourism and recreation (McCarth 2013)], societal [e.g. potable water availability (NOAA 2016)], and ecological [littoral zone species survival (Hynes 1961)] implications.

So far, worldwide WLF forecasting research has focused on large lakes (Table 1), whose navigable surfaces and water resources are important not only locally but also globally. However, while small lakes (i.e. 0.05 km2 < area < 10 km2; Silvestri 2010) are of lesser global significance, they are often very important to local ecosystems and economies. This constitutes a valid  reason to attempt to forecast WLF in the smaller and far more numerous small lakes which dominate the landscape of high-latitude regions where the effects of climate change are particularly evident (Kundzewicz 2011). Particularly susceptible to natural or anthropogenic changes, these smaller lakes constitute an essential element of local ecosystems and harbour habitats which support numerous plant and animal species. As a result, these lakes represent an ideal indicator of the mainly climate-driven changes that may occur in a given region’s water resources. Based on the methods of WLF forecasting developed for large lakes, forecasting applications in this particular study were developed by means of artificial neural networks (ANNs) and wavelet transforms (WTs). While the effectiveness of ANNs has been documented in the literature, data pre-processing by WT has not attracted much attention in the field of WLF forecasting. Given the lack of studies that have explored artificial intelligence and WT methods for WLF forecasting in small lakes, the present study aimed to evaluate, for the first time, whether: (1) small lake water levels could be accurately forecast using ANNs, (2) ANNs fed with wavelet-transformed data would yield better results in terms of forecast accuracy, and (3) certain input data had a greater impact on the accuracy of monthly WLF forecasting.

Table 1 Overview of recent literature on forecasting lake levels
Full size table

Study area

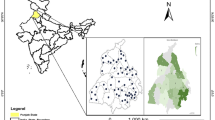
Lake Biskupinskie is located in north-central Poland (Fig. 1), a young, post-glacial landscape formed over the last glaciation (which ended approximately 12,000 years ago). Characterized by one of the lowest total annual precipitation rates in Poland (≈ 500 mm year−1), in recent years the region has shown a clear upward tendency in total annual evaporation, which recently exceeded 800 mm year−1 (Piasecki and Marszelewski 2014). This rise in evaporation was linked to recent increases in wind speed, air temperature, and relative sunshine duration, along with a decrease in humidity. Therefore, climatic factors have the greatest impact on the regions’ hydrological conditions. Data on precipitation, water level, etc., were taken from the IMGW PIB (Institute of Meteorology and Water Management–National Research Institute of Poland). Meteorological parameters were measured in Kołuda Wielka (52.73N, 18.14E–80.8MASL), which is 28 km from Biskupinskie Lake. The water level was measured by means of a staff gauge, which is located at 52.79N, 17.74E, and 78.68MASL. In the case of water-level measurements, no missing data were observed.

Fig. 1
figure 1

Study location

Full size image

Supplied with water from a small run-off stream (Gąsawka), Lake Biskupinskie has a surface area of 1.16 km2, a mean depth of 5.5 m, a maximum depth of 13.7 m, an estimated volume of 6.4 × 106 m3, and a per surface area surface outflow of 9.0–10.8 m3 h−1 km−2 (Markiewicz 2005). The Biskupinskie Lake basin, comprising the upper and middle parts of the Gąsawka river catchment, is characterized by a dense network of watercourses and drainage ditches. In 2004, monthly monitoring of the flow values along the entire length of the Gąsawka River was carried out. The average value of the flow below Biskupinskie Lake was 0.131 m3 s−1. (Extreme values were 0.04 and 0.296 m3 s−1; Markiewicz 2005.) In the area of the Biskupinskie Lake basin, arable land (59%) and forests (26%) dominate. Natural watercourses, including the Gąsawka river, were deepened and their beds straightened in the past. The main melioration works were carried out in the nineteenth century, and after the Second World War (in the 1950s and 1970s) the drainage network was additionally compacted. Based on nineteenth- and twentieth-century cartographic materials, water levels were relatively high (79.6 m AMSL) over this period. In the 1930s, the water level dropped significantly and revealed the remains of a Sorbian defensive settlement (Niewiarowski 1995), which were extensively excavated and studied. Until the early 1990s, Lake Biskupinskie’s water-level amplitudes often exceeded 1 m, causing significant decay at the archaeological site, where wooden construction elements remained well preserved when submerged under water, but rapidly decayed when exposed to the open air. In 1992, a weir (without spillway structures so the weir does not control the outflow volume) was constructed to maintain a relatively high water level in the lake and to guarantee optimal conditions for the preservation of the wooden structures. This archaeological site is a remnant of an ancient settlement created in this place most probably in the winter of 738 BC (Niewiarowski 1995). The archaeological significance of this place is very large, which is why it is protected by ensuring an adequate level of water in the lake (Fig. 2).

Fig. 2
figure 2

Lake Biskupinskie average monthly water-level fluctuations (1957–2014)

Full size image

Methods

Related work

The main factors influencing WLF include climatic conditions, lake size and morphometric parameters, catchment size, water supply (e.g. groundwater, precipitation, inflow from rivers and other surface water flows), and human activities. While a large number of studies have tackled the problem of WLF forecasting (Table 1), the multiplicity of factors influencing WLF makes it extremely difficult to create a universal forecasting method capable of performing effectively in all cases (Khatibi et al. 2014). Using a number of similar but non-identical forecasting methods and addressing an individual or small number of lakes, the WLF forecasting applications developed in these studies employed particular sets of presumably relevant input variables without, however, providing any justification for the particular selection. With the myriad of forecasting methods employed, their application to widely differing lakes, the differing nature of the historical time series drawn upon, and the use of different performance indices, studies are almost impossible to compare. Even when the selected criteria enable direct comparison, local conditions may significantly influence model performance, making it perfect for one area but useless in another (Khatibi et al. 2014). In light of the above, and also in an attempt to improve upon traditional artificial intelligence forecasting approaches, a new development in the field of forecasting model development is the creation of hybrid models, most often consisting of one or more artificial intelligence methods with some form of pre-processing approach (e.g. wavelet transforms).

Based on Table 1, Lake Van in Turkey and the Great Lakes in North America have drawn the most attention. Some papers focused on comparing artificial intelligence methods with conventional time-series analysis approaches such as AR or MLR. Others strove to develop novel methods such as ANFIS-GP or methods of adjusting/calibrating models by means of firefly algorithms (FA) or genetic programming (GP). Older methods such as ARMA, MLR, or SARIMA were used as a benchmark to compare with modern approaches which currently consist mainly of various new artificial intelligence methods. Because there is no universal method capable of taking into consideration and detecting all factors influencing time-series variability, some authors combined various approaches creating so-called hybrid models. This research follows this trend by applying WT as a data pre-processing tool and then uses artificial neural networks for forecasting. Results obtained from this hybrid approach were then compared to those of an ANN model which, according to the literature, is superior to most traditional approaches (e.g. ARIMA).

So far only Altunkaynak (2014) has forecasted lake water-level fluctuations by means of WT-ANN. His proposed model for two large lakes (Lakes Michigan and Huron) outperformed traditional approaches based on single multilayer perceptron and fuzzy logic. However, Altunkaynak (2014) did not consider the impact of meteorological parameters on water levels, but rather only used preceding water levels as exogenous variables. In contrast, in the present study water levels were forecast for a small lake, while taking into account the impact of meteorological parameters.

ANN: artificial neural network

Artificial neural network is a general term for mathematical structures which carry out given calculations or signal processing tasks through an array of individual artificial neurons (a.k.a. processing elements) inspired by neurons in the human brain (Fig. 3). ANNs are well suited to complex, nonlinear problems, where interdependence between exogenous and endogenous variables is often hidden and hardly distinguishable. Besides the examples of ANN application in limnology mentioned in the introduction, ANNs are extensively used in fields such as geophysics (Wiszniowski et al. 2014; Samui and Kim 2014); climatology (Chattopadhyay 2007); medicine (Baxt 1995; Smyczyńska et al. 2015); resource or energy demand (Khwaja et al. 2015; Szoplik 2015; Piasecki et al. 2016); renewable-resource availability forecasting (Cadenas and Rivera 2009; Mellit and Pavan 2010); and drought forecasting (Adamowski and Chan 2011).

Fig. 3
figure 3

Neuron model which may be located in the hidden and output layers

Full size image

One of  the most popular types of feed-forward networks, the multilayer perceptron (MLP), consists of a single input layer, a variable number of hidden layers, and a single output layer. The number of neurons in an output layer is equal to the number of dependent variables (in this case, one—water level), while in the input layer the number is equal to the number of exogenous variables, both quantitative and qualitative.

In this study, linear, logistic, hyperbolic tangent, exponential, and sigmoid functions were tested as the activation function in the hidden and output layers. The number of hidden neurons in the hidden layer ranged from 1 to 25. During the learning process, the sum of squares (SOS) served to assess model performance. The networks were taught by means of different variants of the Broyden–Fletcher–Goldfarb–Shanno (BGFS; Shanno 1985) algorithms. The initial set of input data was divided into calibration (70%), validation (15%), and testing (15%) subsets by means of a random sampling method and remained constant over the whole study and across all models tested. (One hundred calibration cycles were used for the ANNs.)

WT: wavelet transform

From a historical point of view, wavelets are new as a mathematical tool, but have their mathematical roots in the works of Joseph Fourier (1768–1830). Recently, studies incorporating wavelets have been conducted in the areas of hydrology (Lafrenière and Sharp 2003; Rajwa-Kuligiewicz et al. 2016); manufacturing processes/fault detection (Kasashima et al. 1995; Jin and Shi 2001); signal processing (Sundararajan 2015); medicine (Faust et al. 2015); forecasting (Chaturvedi et al. 2015); and power loads (Jurasz and Mikulik 2016); among others. Multiresolution analysis techniques, such as the wavelet transform (WT), which are widely employed in science and engineering, have received very little attention in water-level forecasting. An approximation technique based on low-pass filters, WT seeks to capture the coarse signal approximation, and high-pass filters, which are designed to provide more accurate approximations when applied to a non-stationary time series.

Wavelet is a mathematical function characterized by a null mean value and finite signal power, which also takes zero values beyond certain finite intervals. These features make it stable in both time and frequency domains, such that both time and frequency localizations can be delivered simultaneously (Mallat 1989). The WT is very similar to the Fourier transform, but the main difference is that the latter decomposes the signal into sines and cosines which are functions localized in Fourier space, whereas wavelet transform applies functions which exist in both real and Fourier space.

There are two different versions of WT: continuous and discrete. The first is very similar to the short-time Fourier transform, where the signal is divided into segments by means of a movable time window. In the case of continuous wavelet transform (CWT), the scanning window is in the form of a wavelet function. Comparatively, the discrete WT is not only a digital version of CWT, but decomposes the signal into approximations/scale (the coarse part) and details (the accurate part).

From a mathematical point of view, WTs are constituted of two parts (Joo and Kim 2015): scale \(\phi \left( {\text{t}} \right)\) and details \(\psi \left( {\text{t}} \right)\), given as:

$$\phi_{j,k} \left( t \right) = 2^{{\frac{j}{2}}} \phi \left( {2^{j} t - k} \right)$$
(1)
$$\psi_{j,k} \left( t \right) = 2^{{\frac{j}{2}}} \phi \left( {2^{j} t - k} \right)$$
(2)

where j denotes the scaling parameter and k denotes the translation index. These functions are subject to the following constraints (Joo and Kim 2015):

$$\begin{gathered} \int {\phi (t){\text{d}}x} = 1 \hfill \\ \int {\psi (t){\text{d}}x} = 0 \hfill \\ \phi (t),\psi (t) \in L^{2} {\mathbf{\mathbb{R}}} \hfill \\ \end{gathered}$$
(3)

According to Joo and Kim (2015), \({\text{L}}^{2} \left( {\mathbb{R}} \right)\) is a space of square integrable real function defined on the real line \({\mathbb{R}}.\) Based on these equations, the signal can be then decomposed into a set of approximations and details. The reconstruction of the signal has been described in the work of Burt and Adelson (1983).

In the present study, WT was used to decompose the time series of water levels into various components, after which approximations at five levels of decomposition were used as input to WT-ANN models. The meteorological parameters of evaporation and precipitation were not subjected to WT. The spectral bands of WT can be selected based on the power distribution (Altunkaynak 2014), where bands which have several peaks are selected for further study. Altunkaynak (2014) states that so far no universal method/rule has been developed to divide time series into different decomposition levels. In this study, the approach hinged on the criterion of the mean relative error between the approximation and the original time series (Nalley et al. 2013). This analysis pointed to the use of five levels of decomposition.

The effect on forecasting model accuracy according to the wavelet applied—Daubechies (db2, db3, db4, db5); Coiflet (coif1, coif 2, coif 3, coif4, coif5); Symlet (sym2, sym3, sym4, sym5); Discrete Meyer; Haar; Biorthogonal (bior1.1, bior1.3, bior1.5, bior 2.2, bior2.4); and ReverseBior (rbio1.1, rbio1.3, rbio1.5, rbio2.2, rbio2.4)—was also assessed.

The ANN models were run in the Statistica software package (StatSoft, Tulsa, OK), while WT was performed using MATLAB 2015a.

Input selection

Previous studies imply that the most commonly used lake-level forecast input variables are: evaporation, precipitation, and previous monthly mean lake water levels (Abrahart et al. 2012). In this study, eight models differing in input variable sets were investigated (Table 2); however, various other combinations of inputs were formerly considered. The basic statistical parameters of the subsets considered are given in Table 3. Table 3 briefly summarizes the performance of all investigated models by means of the RMSE criterion; additionally, the values for calibration and validation phases are given.

Table 2 Model input variable sets and wavelets used, subscripts t–x represent mean monthly variable values from x months prior to the present
Full size table
Table 3 Univariate statistics of input variables
Full size table

Prior to building the variables of these eight models (M1–M8), a preliminary analysis was conducted on models fed only with a variety of wavelets from the two previous months’ water levels. This analysis (Fig. 4) sought to single out those mother wavelets which enabled simple models to perform best. Analysis based on forecasting models which used only wavelet-derived input data revealed better results from the perspective of the RMSE value for BIOR2.4 and DB2, whereas COIF2 and BIOR2.2 performed worse. Their RMSE values for the testing subset were: 1.872, 1.968, 2.132, and 2.154, respectively. An example of a five-level decomposition using db2 wavelets is presented in Fig. 5. In the models developed, no weather factors which might have an impact on water level, other than evaporation and precipitation, were taken into account; irradiation, relative humidity, and temperature, for example, were disregarded. The reason for not taking into account weather variables in this study was because the available time series had many missing values—in some cases over 20%. When the missing values were replaced with the means usually observed over the given time of the year, the correlation coefficient between those time series and the water level was significantly lower than in the case of evaporation and precipitation. Therefore, only those two parameters were considered.

Fig. 4
figure 4

Examples of wavelets used in the most efficient models. From right to left: top row: Daubechies db2 and Coiflets coif2; bottom row: Biorthogonal bior2.2 and bior2.4

Full size image
Fig. 5
figure 5

Decomposed and original time series (d1, d2, d3, d4, d5 and a5) using db2 wavelets as calibration values

Full size image

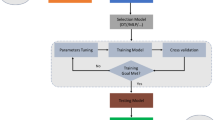
Figure 6 presents a general schematic of model development. Prior to model creation, input data sets underwent a normalization procedure (Eq. 4); once forecasts were obtained, these were then converted back to their previous range (Eq. 5). This allowed an unbiased assessment of model performance, compared to expert judgment which may be skewed when values range from − 1 to 1.

$$x_{\text{norm}} = \frac{{x_{i} - x_{ \hbox{min} } }}{{x_{ \hbox{max} } - x_{ \hbox{min} } }}$$
(4)
$$x_{i} = x_{n} \left( {x_{ \hbox{max} } - x_{ \hbox{min} } } \right) + x_{ \hbox{min} }.$$
(5)
Fig. 6
figure 6

Flowchart for model creation

Full size image

Performance indices

The forecasting accuracy (lead time 1 month) of the presented models was evaluated for the testing data sets using (103-element testing set) the statistic parameters of MAE, RMSE, MSE, R2 and MAPE:

$${\text{MAE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {L_{i} - L_{i}^{*} } \right|$$
(4)
$${\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {L_{i} - L_{i}^{*} } \right)^{2} }$$
(5)
$${\text{MSE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {L_{i} - L_{i}^{*} } \right)^{2}$$
(6)
$$R^{2} = \frac{{\left( {\mathop \sum \nolimits_{i = 1}^{n} \left( {L_{i} - \overline{{L_{i} }} } \right)\left( {L_{i}^{*} - \overline{{L_{i} }} } \right)} \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {L_{i} - \overline{{L_{i} }} } \right)^{2} \mathop \sum \nolimits_{i = 1}^{n} \left( {L_{i}^{*} - \overline{{L_{i} }} } \right)^{2} }}$$
(7)
$${\text{MAPE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {\frac{{L_{i} - L_{i}^{*} }}{{L_{i} }}} \right|$$
(8)

where Li, \(L_{i}^{*}\) and \(\overline{{L_{i} }}\) are the observed, predicted and mean observed values of water level, and n is the total number of observations. There exists some controversy over these criteria, regarding the comparison of models applied to different data sets (Armstrong and Fildes 1995). This can be resolved by means of the MASE (mean absolute scaled error) introduced by Hyndman and Koehler (2006). However, this issue falls beyond the scope of this paper. In general, the smaller the value of the error measure, the better the performance of the forecasting model.

Results

The performance of all eight models (Table 2) was evaluated. The R2 between observed and 1-month-in-advance forecast lake water levels (Fig. 7), and the accuracy statistics of MAPE, RMSE, MAE and MSE (Fig. 8) served to determine which model most accurately forecast lake water levels. On this basis, the best-performing model was M1, which had input variables of: (1) water level from two previous periods (Lt−1 and Lt−2) decomposed by WT using db2 and bior 2.4 mother wavelets; (2) non-decomposed meteorological variables of precipitation and evaporation, from two previous periods (Pt−1 Pt−2 Et−1 Et−2, respectively); and (3) binary variables relating to months (1–12) and backlogging (0–1).

Fig. 7
figure 7

Scatter plots of M1–M8 models in the testing period

Full size image
Fig. 8
figure 8

MAPE, RMSE, MAE, and MSE values for selected models. MAPE—mean absolute percentage error, RMSE—root mean squared error, MAE—mean absolute error, MSE—mean squared error

Full size image

Comparatively, M2, which differed from M1 in not employing meteorological variables, performed better in terms of the MAPE and MAE criteria (Fig. 8). However, in this case it was impossible to unequivocally state whether meteorological variables had a significant impact on model performance. The present study was limited in the fact that WT was not applied to meteorological variables, a decision which was based on the rapidly growing number of possible input set combinations given the multitude of possible wavelets and decomposition levels which could be applied to them. Similarly, Altunkaynak (2014) used non-WT-decomposed meteorological variables in the forecasting of lake water levels.

Models M4, M5 and M6 were based on the same wavelet bior 2.4, but only M4 and M6 used meteorological variables. Of these two, the input variables used in M6 were taken from only 1 month back, rather than two in the case of M4. Models M4–M6 showed similar R2 criteria (all > 0.9887; Fig. 7). However, the remaining performance measures unambiguously indicate the superior performance of the M4 model (Fig. 8).

In the case of the M7 and M8 models, where wavelet transformation was not applied to the prior water-level data, the accuracy was poorer than that of their equivalent WT-transformed counterparts, M1 and M2 (Figs. 7, 8). Model M7 performed slightly better than model M8 (which did not have meteorological variables), but the values of the MAPE, RMSE, MAE and MSE criteria were still on average 30 times greater than for the M1 model (see Fig. 8). The performance was mainly poor with regard to the MSE criterion, which accentuates gross errors. Comparison between the performance of M1–M6 WT models and non-WT M7 and M8 models clearly demonstrates the superiority of ANN models employing WT pre-processed input variables.

Discussion

As shown by the results, it is possible to effectively predict water levels using ANN and WT in small post-glacial lakes. As already mentioned at the outset, up until now knowledge about predicting the water level of lakes has focused on areas of large surface area and volume. This study focused on a different case—a small lake; it was thus possible to compare the obtained results with previous studies on larger lakes. It was particularly interesting to examine the meaning of individual variables in the context of the accuracy of the WLF forecast. Small lakes are much faster and more responsive to changing volume and vertical exchange than large lakes. The present analysis did not unequivocally indicate the importance of meteorological variables in WLF forecasting; however, it should be noted that in the present study mean or cumulative monthly values of individual variables were used. Consequently, a situation might have arisen in which intense precipitation occurred toward the end of the month, leading to an increased water level in the following month, which then stabilized due to outflow. Another important issue is the delay in water supply from the catchment; a relatively low terrain gradient leads to minimal surface water supply. These factors directly affect the relationship between meteorological parameters and water level. These conclusions, however, cannot be generalized to all lakes with similar morphometry, because the decisive factor here is the character of the catchment. The size of the basin, its shape (longitudinal, circular), the type of land cover, land morphology (including land denivelation) and the density of the watercourse and channel networks determine the surface supply of lakes. In the present case, the aforementioned factors resulted in the low significance of meteorological variables in WLF forecasting. In creating a 1-month-ahead WLF forecast (as in this study), the most important input variable is water levels from previous periods. Water levels are the principal variable determining the forecast’s accuracy; the remaining variables only slightly modify the forecasted value. This conclusion is in accordance with most of the studies on WLF forecasting in lakes. In the large lake studies mentioned earlier (Table 1), the multitude of forecasting performance measures render it almost impossible, as noted by Armstrong and Fildes (1995), to compare two models created for different time series. In this study, WLF forecasting via ANNs based on data transformed with wavelets was determined to be more effective than using raw data in ANNs. This confirms the conclusions presented by Noury et al. (2014).

Knowledge about WLF may be used in the construction of small hydropower plants, which are a source of renewable energy. In Poland, the construction of small hydropower plants has been a very popular topic for over a dozen years. Knowledge about WLF in lakes is also useful for sustainable water resources management, as well as in fisheries, agriculture, industry, tourism and recreation. The activities of these components of the economy are often based on lake water resources. Their excessive exploitation, which is often associated with a lack of knowledge regarding water levels in lakes, may lead to irreversible changes and degradation of aquatic ecosystems. This study points to an additional practical aspect of WLF forecasting of lakes—the protection of archaeological sites associated with aquatic environments. As mentioned earlier, submerged archaeological sites often require maintaining an appropriate level of water in the lake, ensuring the permanent preservation of the submerged artefacts.

The research described in this paper focused on forecasting WLF in a single lake, which was an approach used by most of the studies that have explored the same topic. The focus on one lake ensures the possibility of detailed tracking of any conditions that may affect the WLF forecasting process. However, the possibility of extrapolating the obtained methods and results to other lakes is limited. One question is whether it is possible to create one universal model that allows for forecasting the water level in different lakes (including in terms of morphometry, catchment size, hydrological type, and climatic conditions)? Because there is such a wide variety of local conditions that determine WLF in lakes, this task is difficult or even impossible. One solution would be to focus on lakes that are homogeneous in some respects (e.g. size, supply or climate).

Conclusions

Research conducted on small surface area lakes is not common; however, numerous arguments presented in this paper make it clear that there is a pressing need to investigate the characteristics of these small water ecosystems, particularly with regard to water-level fluctuations and changes in water resources. Small post-glacial lakes are not a frequent object of scientific analysis due to their relatively small significance in terms of global transformations of the natural environment. However, their role in the local water ecosystem is very large. As a result, they are a useful study site to monitor climate fluctuations on a smaller scale (catchment areas, physical geographic regions). The main goal of this paper was to explore whether it is possible to accurately forecast water levels in relatively small lakes. In the case of this study, this was achieved by means of a hybrid WT-ANN model. Wavelet transform pre-processing of input data led to better forecasts. The contribution of this study lies in the confirmation of the two hypothesis of the study, namely that: (1) it is possible to accurately forecast water levels of relatively small lakes, and (2) the application of different wavelets to the artificial intelligence method of ANNs yields better predictions than simple ANNs.

There are several interesting directions for future research, including: (1) a detailed analysis of the optimal level of wavelet decomposition and selection of wavelet input sets (approximations and details); (2) the application of WT not only to water-level data, but also to meteorological parameters; (3) WLF forecasting in a relatively homogenous group of lakes; and (4) WLF forecasting without taking into account the water-level variable from the previous period.