1 Introduction and results

The problem we deal with in this paper emerged from columns written by Martin Gardner in 1966 and 1975 [5, 6], where he popularized a previously unpublished question due to R. B. Britton. The problem is to pack the first n consecutive squares (i.e. the ones with edge lengths \(1,\ldots ,n\)) into a smallest containing square (with integer edge length). Here and throughout the paper we consider only the case where the squares have to be packed parallel to the axes (i.e. rotation is not allowed) and we have to pack them without overlapping. Other natural assumptions are that the squares are allowed to touch each other and that they cannot be split. For this problem, Gardner [6] listed the best possible (tight) results up to \(n=17\) (based on earlier works). An upper bound (UB) is best possible if it meets a valid lower bound.

The packing of consecutive squares has become a benchmark problem for general square packing problems, e.g. it is used to test more general rectangle packing algorithms [14, 16, 21]. Rectangle packing has been applied in VLSI design, and also can be used to model some real-world problems like scheduling, cutting stock and pallet loading problems. In most of these areas rotation of the rectangles is allowed; however, there are some problems, for example in scheduling, where rotation is forbidden.

The current best upper bounds for our problem can be found on the webpage [22], searching for the integer sequence A005842. There, the best known UB(n) values are listed till \(n=56\) (most of them are tight), where UB(n) is the upper bound for our problem with a given parameter n. The best lower bounds for large values of n come from the simple fact that we can get a fairly good estimate by rounding up the square root of the total area of the squares, i.e. in our case we get the value \(LB_0:=\lceil \! \sqrt{\sum _{k=1}^n k^2} \rceil = \lceil \!\sqrt{n(n+1)(2n+1)/6)} \rceil \). Tightness is not proved for the cases \(n=38, 40, 42, 48, 52, 53\) and 55, while the other values of UB(n) given in [22] are proved to be tight for \(1\le n\le 56\). The latest results have been achieved by Hougardy [8]. He showed that \(UB(28)=89\), \(UB(32)=108\), \(UB(33)=113\), \(UB(34)=118\), and \(UB(47)=190\), and proved that these upper bounds are best possible; i.e., \(LB_0+1\) is a valid matching lower bound in these cases. An interesting special case of the problem is \(n=24\), which was unsolved until 2004. As proved earlier [23], \(n=24\) is the unique non-trivial case where \(\frac{n(n+1)(2n+1)}{6}\) is an integer. However, while \(LB_0(24)=70\), the optimum is 71 as proved by Korf [15].

A related problem is to pack an arbitrary set of squares with a total area of at most 1 into a rectangle of minimum area. In this line of thinking it was proved in [17] that any rectangle of area 2 suffices, provided that its side lengths are not smaller than the largest square to be packed. A stronger upper bound can be derived from [13], stating that a covering rectangle with an area of at most \(\sqrt{8/3}<1.633\) can be given for any input of this type. This result was further improved to 1.53 in [18], and to 1.4 in [7]. Moreover, several papers deal with higher dimension; see e.g. [1, 12, 19, 20]. Gap-free arrangements, called perfect packings, of the infinite series of squares and boxes of side lengths \(\{n^{t}\}_{n\ge 1}\) for a certain range of t have also been considered; see [3, 9,10,11, 20].

A similar question, where the container is a square was answered in [2]. Here the authors proved that any set of squares can be packed into the unit square if (i) the total area of the squares is at most 5/9 and (ii) none of the squares has edge length larger than 1/2. They also proved that 5/9 is the best possible such value. We mention here that in their packing, the patterns used fulfill the guillotine pattern properties. Their packing is similar to the First Fit Decreasing Height (FFDH) heuristic of [4] designed for the two-dimensional strip packing problem, but they used it both horizontally and vertically.

Our results To the best of our knowledge, there are no asymptotic-type guarantees (upper bounds) to the problem of packing consecutive squares into a square. We fill this gap of the literature by delivering the first results of this nature, considering both guillotine-type packings and unrestricted axis-parallel packings.

We state our results in terms of packing squares into rectangles, from which packing into squares will be a corollary. To simplify formulas we introduce the notation \(A_n:=\frac{n(n+1)(2n+1)}{6}\) and \(N:=\sqrt{A_n}\). Hence \(LB_0=\lceil N \rceil \), and no smaller square can contain a packing of the squares of sizes (= side lengths) \(1,2,\dots ,n\). We prove that a slightly bigger square admits a packing.

Theorem 1

There exists a constant \(c<1\) such that the square of size \(N+cn\) admits a guillotine-type packing of the squares of sizes \(1,2,\dots ,n\).

From the proof of the more general Theorem 4 in Sect. 2 it follows immediately that any \(c>7/8\) is a suitable choice for \(n\ge n_0(c)\). In the concluding section we shall indicate ways for improvements yielding a smaller constant. Even better bounds can be proved if the structure of cuts is not restricted, as shown in following result.

Theorem 2

For every \(\epsilon >0\) there exists a packing of the squares of sizes \(1,2,\dots ,n\) into a square of size \(N+(\frac{1}{2}+\epsilon )\, n+O (\!\sqrt{n})\), if n is sufficiently large with respect to \(\epsilon \).

In Sect. 3 we prove this result in the following more general form.

Theorem 3

Let c be a fixed real number, \(0<c<1\). For every \(\epsilon >0\) there exists a constant \(C'=C'(\epsilon ,c)\) such that, if \(N_1N_2 \ge A_n\) and \(cN_2\le N_1\le N_2\), then the squares of sizes \(1,2,\dots ,n\) can be packed into an \((N_1+n) \times (N_2+\epsilon n + C'\!\sqrt{n})\) rectangle.

Certainly the \(O(\!\sqrt{n})\) term becomes superfluous for sufficiently large \(n\ge n_0(\epsilon ,c)\).

Fig. 1
figure 1

Scheme of recursion

Full size image

2 Guillotine cutting

Here we prove Theorem 1 in the following more general form.

Theorem 4

If \(N_1\) and \(N_2\) are real numbers such that \(N_1N_2 \ge A_n\) and \(N_1\le N_2\), then an \((N_1+n) \times (N_2+cn)\) rectangle admits a packing of the squares \(1,2,\dots ,n\) with guillotine cutting, where c is a suitable constant smaller than 1.

In the argument below, it is not our aim to optimize the value of c; we shall see that \(c=3/4\) surely works. Then, putting \(N_1=N-n/8+r(n)\) and \(N_2=N+n/8+r(n)\) we see that the condition \(N_1N_2\ge A_n=N^2\) can be satisfied with a suitably chosen function \(r(n)=O(\!\sqrt{n})\), hence implying Theorem 1 for any \(c>7/8\) and large enough n.

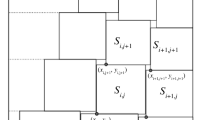
The packing will be arranged in the decreasing order of the sizes of the squares, i.e. in the order n, \(n-1\), \(n-2,\dots ,2,1\). The packing is done in several phases; the rough structure of Phase 1 and Phase 2 in cases where \(N_1\) and \(N_2\) are not very far from each other—say, \(N_1>N_2/8\) or so—is shown in Fig. 1.

In Phase 1 we deal with the squares of size i in the range \(n/2 - x < i \le n\), for a relatively small x, as will be explained later. We consider a rectangle whose width is \((N_1+n)\) and height is \((N_2+cn)\), and take horizontal edge-to-edge cuts resulting in new rectangles \(R_1,R_2,\dots ,R_m\), into which squares are placed side by side. Each \(R_j\) will be filled to a width between \(N_1\) and \(N_1+n\); we denote the height of \(R_j\) by \(w_j\), which is the size of the largest square in \(R_j\). The starting height is \(w_1=n\). We pack the squares \(n,n-1,\dots ,w_2+1\) into \(R_1\) to reach width \(N_1\) or a little more; that is, \(\sum _{i=w_2+2}^n i < N_1\) and \(\sum _{i=w_2+1}^n i \ge N_1\).

The phase continues analogously: If \(R_{j-1}\) has been constructed and packed, let \(w_j\) be the size of the largest square which has not yet been packed, and pack the squares \(w_j,w_j-1,w_j-2,\dots ,w_{j+1}+1\) into \(R_j\)—which is an \((N_1+n) \times w_j\) rectangle—to reach width just \(N_1\) or slightly beyond. This procedure terminates when also the rectangle \(R_m\) containing the square \(\lfloor n/2 \rfloor + 1\) is packed up to at least \(N_1\). This condition fixes the value of x, defined as a non-negative integer if n is even, or 1/2 plus a non-negative integer otherwise, such that the inequalities \(\sum _{i=n/2- x +2}^{w_m} i < N_1 \le \sum _{i=n/2- x +1}^{w_m} i\) hold. Hence, the number of squares packed in Phase 1 is \(n/2 + x\), and the largest unpacked square has size \(n':=n/2-x\).

The total height of this partial packing is \(H:=w_1+\cdots +w_m\). Phase 2 deals with the rectangles \(n',n'-1,\dots ,n'\!/2-x'\) with some small \(x'\). If \(N_1\le N_2-H\) holds, then Phase 2 continues the procedure with horizontal edge-to-edge cuts exactly in the same way as we did in Phase 1, defining e.g. \(N_1':=N_1\) and \(N_2':=N_2-H+cn-cn'\). This leaves much space (namely, with width n) beyond \(N_1'\) horizontally and \(cn'\) space beyond \(N_2'\) vertically, keeping \(N_2'\ge N_1'\). Otherwise, if \(N_1 > N_2-H\), we switch the roles of the two parameters so that \(N_1':=N_2-H+cn-n'\) and \(N_2':=N_1+n-cn'\). In that case, Phase 2 creates vertical edge-to-edge cuts, placing the next squares on the top of each other and not leaving an empty vertical space more than \(n'\). In either case we provide at least a blank rectangle \((N_1'+n') \times (N_2'+cn')\) for the packing of the squares of sizes at most \(n'\). Hence, if we prove that \(N_1'N_2'\ge A_{n'} = \sum _{i=1}^{n'} i^2\) holds, it will imply that all squares are properly packed after at most \(\lceil \log _2 n \rceil \) phases, because there is always at least a halving of the number of items to pack.

Let us recall that in Phase 1 every \(R_j\) (\(1\le j\le m\)) is filled to width \(N_1\) or beyond, but this property does not remain valid if we remove any one square from the contents of \(R_j\). We are going to apply the latter fact for the largest square in each rectangle and derive an upper bound on how large area remains blank in \(R_1\cup \cdots \cup R_m\) within width \(N_1\). Choose any one j, let \(w=w_j\), and assume that exactly \(k+1\) squares are packed in \(R_j\). We know that

$$\begin{aligned} N_1 > \sum _{i=1}^k (w-i) = kw - \frac{k(k+1)}{2} = k \biggl ( w - \frac{k+1}{2} \biggr ) . \end{aligned}$$

There is no blank space above the square of size w, and for \(i=1,\dots ,k\) the blank area above the square of size \(w-i\) is \(i\cdot (w-i)\). Hence, using that the sum of squares of the first k positive integers is \(A_k\), the total blank area in this rectangle is

$$\begin{aligned} \sum _{i=1}^k i\, (w-i)= & {} \! {k+1 \atopwithdelims ()2} w - \frac{k(k+1)(2k+1)}{6} = \frac{k+1}{2} \, k \biggl ( w - \frac{2k+1}{3} \biggr )\\= & {} \frac{k+1}{2} \, k \biggl ( w - \frac{k+1}{2} \biggr ) - \frac{k+1}{2} \, k \, \frac{k-1}{6}\\< & {} \frac{k+1}{2} \, k \biggl ( w - \frac{k+1}{2} \biggr ) < \frac{k+1}{2} N_1 \, . \end{aligned}$$

Summing for \(j=1,\dots ,m\) we see that the total blank area in \(R_1\cup \cdots \cup R_m\) containing the \(n-n'\) largest squares is smaller than \(\frac{1}{2}(n-n')N_1\). The total area of squares packed in Phase 1 is \(A_n-A_{n'}=\sum _{i=n/2-x+1}^n i^2\). Then the height packed so far is

$$\begin{aligned} H = \sum _{i=1}^m w_i < \frac{A_n-A_{n'}+\frac{1}{2}(n-n')N_1}{N_1} \le N_2 - \frac{A_{n'}}{N_1} + \frac{n}{2} - \frac{n'}{2} \, . \end{aligned}$$
(1)

Hence \( N_2-H > A_{n'}/N_1 - \frac{1}{2}n + \frac{1}{2}n'\). What remains is the following:

  • squares of sizes \(1,2,\dots ,n'\), having total area \(A_{n'}\), to be packed;

  • a rectangle for the packing, with side lengths at least \(N_1'+n'\) and \(N_2'+cn'\).

Depending on whether or not the cutting direction has been switched from horizontal to vertical, we need to verify the following for a suitable value of c :

  1. (a)

    If \(N_1\le N_2-H\), then \(N_1'N_2' = N_1 (N_2-H+cn-cn') \ge A_{n'}\).

  2. (b)

    If \(N_1 > N_2-H\), then \(N_1'N_2' = (N_2-H+cn-n') (N_1+n-cn') \ge A_{n'}\).

Case (a) is implied by Eq. (1) immediately for any \(c\ge 1/2\) :

$$\begin{aligned} N_1'N_2' = N_1 (N_2-H + cn-cn') > N_1 \Bigl (\frac{A_{n'}}{N_1} + \frac{(2c-1)(n-n')}{2}\Bigr ) \ge A_{n'} . \end{aligned}$$

Case (b) is not hard either. First apply Eq. (1) also here, to obtain

$$\begin{aligned} N_1'N_2'= & {} (N_2-H+cn-n') (N_1+n-cn') \\&\qquad \quad >&\Bigl (\frac{A_{n'}}{N_1} + \frac{(2c-1)n}{2} - \frac{n'}{2} \Bigr ) \bigl (N_1+n-cn'\bigr )\\= & {} A_{n'} + \frac{(n-cn') A_{n'}}{N_1} + \frac{(2c-1)n-n'}{2} \Bigl (N_1+n-cn'\Bigr ) . \end{aligned}$$

The second term in the last line is positive. Taking into account that \(n'\le n/2\), it is also clear that \((2c-1)n\ge n'\) holds whenever \(c\ge 3/4\). Thus, the sum is at least \(A_{n'}\) for this choice of c.

It is clear from the procedure that the structure is a guillotine cutting. This completes the proof.

3 Unrestricted packing

Here we prove Theorem 3—packing all squares of sizes between 1 and n into an \((N_1+n) \times (N_2+\epsilon n+O(\!\sqrt{n}))\) rectangle—with a similar argument as in the proof of Theorem 1, using here a denser packing inside the subrectangles. Throughout the proof we assume that \(\epsilon >0\) is a parameter independent of the input size, and also without loss of generality that \(N_1,N_2\) are shrunk to satisfy \(N_1N_2 = A_n\). Furthermore, \(c_1,c_2,\dots \) denote absolute constants which are also independent of \(\epsilon \), while \(\epsilon _1\) and \(\epsilon _2\) will be very near to \(\epsilon \). The \(O(\!\sqrt{n})\) term, whose hidden constant depends on the parameters \(\epsilon \) and c of Theorem 3 but on nothing else, will be adjusted at the end.

This procedure applies a two-phase recursion; we consider all squares of sizes \(\gtrsim \epsilon n\) in the first phase and the squares of size i with \(\epsilon ^2 n \lesssim i \lesssim \epsilon n\) in the second phase. Intuitively, the rectangles of the previous construction are put in pairs \((R_{2i-1},R_{2i})\) for \(i=1,2,\dots ,\) the rectangle of odd index is rotated with \(180^{\circ }\), and the gap is eliminated; we illustrate this in Fig. 2. It is also possible that the smallest square on the top hangs over the largest square at the bottom.

Fig. 2
figure 2

Example of a slice in which \(5+8\) squares fit; \(w=w_{2i}\) (for some value i)

Full size image

Originally the height of \(R_{2i-1} \cup R_{2i}\) is \(w_{2i-1}+w_{2i}\), but the size of the last square in \(R_{2i-1}\) is only \(w_{2i}+1\). Hence the two rows of squares can be pushed towards each other by \(w_{2i-1}-(w_{2i}+1)\) because the decrease of square sizes in \(R_{2i}\) is faster than their increase in \(R_{2i-1}\). This operation reduces the blank area considerably. We denote by \(S_i\) the slice of height \(2w_{2i}+1\) derived from \(R_{2i-1} \cup R_{2i}\) in this way. For complete slices an even number of rectangles \(R_j\) is needed; hence we fill horizontal rectangles \(R_1,R_2,\dots ,R_m\) up to \(N_1\) or slightly beyond (as in the case of guillotine cuts) by packing the squares of sizes \(n,n-1,\dots ,n'+1\) under the following conditions: The rectangle \(R_m\) is packed to at least \(N_1\), m is even, \(n'\le \epsilon n\), and \(A_{n'} \le \epsilon ^3\! A_n\). We take the largest possible such \(n'\); this determines the halting condition for Phase 1.

In the computations below, the \(O(\,.\,)\) terms will always mean functions where the ‘hidden constants’ may only be related to c, never to \(\epsilon \). First of all let us note that the assumptions \(N_1N_2 = \Theta (n^3)\) and \(cN_2\le N_1\le N_2\) imply that both \(N_1\) and \(N_2\) have growth order \(\Theta (n\sqrt{n})\), as \(N\! \sqrt{c} \le N_1 \le N_2 \le N /\!\sqrt{c}\).

Defining \(\epsilon _1 := \root 3 \of {A_{n'}/A_n}\) we see that all squares of size at least \(\epsilon _1 n\) are packed in Phase 1. This follows from the fact that \(xn(xn+1)(2xn+1)> x^3 n(n+1)(2n+1)\) holds for all \(0<x<1\). Also, \(\epsilon _1\le \epsilon \), but \(\epsilon -\epsilon _1\) is rather small, because \(\epsilon n - n' = O(\frac{1}{\epsilon }\sqrt{n})\). Indeed, we have \(N_1=\Theta (n\sqrt{n})\), and the sizes of squares packed in \(R_{m-1}\cup R_m\) are \(\Theta (\epsilon n)\), therefore the number of squares in \(R_{m-1}\cup R_m\) is \(\Theta (\frac{1}{\epsilon }\sqrt{n})\). Moreover, \(A_{\epsilon n} \le \epsilon ^3\! A_n + O(n^2)\) is valid, hence the requirement \(A_{n'} \le \epsilon ^3\! A_n\) yields that the difference between \(\epsilon n\) and the size of the largest square in \(R_{m-1}\)—if the latter is smaller—has an upper bound proportional to \(1/\epsilon ^2\). (Otherwise we would have stopped with \(R_{m-2}\) rather than \(R_m\).)

After the construction of horizontal slices in Phase 1, the procedure is continued in Phase 2 with vertical slices placed on the top of the horizontal slices. Before giving its numerical conditions, let us state and prove several properties. The first claim is width-independent.

\(1^{\circ }\):

If the number of squares packed in \(R_{2i}\) is \(k+1\), then the blank area in \(S_{i}\) is at most \(\sum _{j=1}^k j^2\).

Proof

Denote the height of slice \(S_i\) by \(2w+1\); by construction we have \(w=w_{2i}\). As one can observe, there is a blank unit square surrounded by the four squares \(w-1\), w, \(w+1\), \(w+2\); a blank rectangle of height 1 and width 4 surrounded by the squares \(w-2\), \(w-1\), \(w+2\), \(w+3\); and so on. Generally, for any \(\ell \ge 0\), the width of the unit-high blank rectangle surrounded by the squares \(w-\ell -1\), \(w-\ell \), \(w+\ell +1\), \(w+\ell +2\) is equal to

$$\begin{aligned} \sum _{j=1}^{\ell } (w+j) - \sum _{j=0}^{\ell -1} (w-j) = {\ell +1 \atopwithdelims ()2} + {\ell \atopwithdelims ()2} = \ell ^2 \, . \end{aligned}$$

More precisely, this is the distance between the bottom-left corner of the square \(w-\ell -1\) and the top-left corner of the square \(w+\ell +2\), in the case that the latter also appears in the slice. If the latter is not present, we can still use this formula as an upper bound. This implies the validity of \(1^{\circ }\). \(\square \)

\(2^{\circ }\) :

The number of squares packed in \(S_i\) is \(O(\frac{1}{\epsilon }\sqrt{n})\) for every i, and the number of slices is \(O(\sqrt{n})\).

Proof

Recall that both \(N_1\) and \(N_2\) have growth order \(\Theta (n\sqrt{n})\). Moreover, since every packed square has size \(\gtrsim \epsilon n\), the number of squares in any \(S_i\) is between \(c_1 \sqrt{n}\) and \(\frac{c_2}{\epsilon } \sqrt{n}\). We have fewer than n squares, therefore the number of slices is at most \(c_3 \sqrt{n}\). \(\square \)

\(3^{\circ }\) :

The largest vertical gap between squares of \(R_{2i-1}\) and \(R_{2i}\) in \(S_i\) is \(O(\frac{1}{\epsilon ^3})\).

Proof

Let \(a_i\) and \(b_i\) be the size of the smallest square in \(R_{2i}\) and the largest square in \(R_{2i-1}\), respectively. Recall that \(a_i \gtrsim \epsilon n\) and \(b_i = a_i+O(\frac{1}{\epsilon }\sqrt{n})\). There are at most \(N_1/a_i+1\) squares in \(R_{2i}\) and at least \(N_1/b_i\) squares in \(R_{2i-1}\). Hence \(w_{2i}-a_i\le N_1/a_i\) and \(b_i-(w_{2i}+1)\ge N_1/b_i - 1\). Since \(N_1=\Theta (n\sqrt{n})\), the height of the largest gap can be estimated as

$$\begin{aligned} 2w_{2i}+1 - (a_i+b_i)\le & {} \frac{N_1}{a_i} - \frac{N_1}{b_i} + 1 = \frac{N_1 (b_i-a_i)}{a_ib_i} + 1\\= & {} \frac{\Theta (n\sqrt{n})\, O(\frac{1}{\epsilon }\sqrt{n})}{\epsilon ^2 n^2} = O\left( \frac{1}{\epsilon ^3}\right) . \end{aligned}$$

The blank area in \(S_i\) is \(O(\frac{1}{\epsilon ^3} n\sqrt{n})\), in agreement with \(1^{\circ }\) as \(k=O(\frac{1}{\epsilon }\sqrt{n})\). \(\square \)

\(4^{\circ }\) :

The total height of the slices is at most \((1-\epsilon _1^3) N_2 + O(\frac{1}{\epsilon ^3} \sqrt{n})\).

Proof

The total area of packed squares is \(A_n-A_{n'} = (1-\epsilon _1^3) N_1 N_2\), moreover by \(3^{\circ }\) the blank area is \(O(\frac{1}{\epsilon ^3} N_1\sqrt{n})\). Since the totally packed width is at least \(N_1\), the assertion follows. \(\square \)

We view the term \(O(\frac{1}{\epsilon ^3} \sqrt{n})\) as an additional slice of that height packed on the top of an \((N_1+n) \times (N_2+\epsilon n)\) rectangle. Then in Phase 2 the slices of vertical position have a blank rectangle \((\epsilon _1^3 N_2 + \epsilon n) \times (N_1+n)\), into which only the squares \(n',n'-1,\dots ,n''+1\) have to be packed, for some \(n''\) (and a blank rectangle has to be left empty for \(n'',n''-1,\dots ,1\)). Hence the slices can be completely packed up to at least \(\epsilon _1^3 N_2\), based again on the principle shown in Fig. 2. Here we require that \(n''\le \epsilon n'\) and \(A_{n''} \le \epsilon ^3 \!A_{n'}\). We take the largest possible such \(n''\); this determines the halting condition for Phase 2. Define \(\epsilon _2 := \root 3 \of {A_{n''}/A_{n'}}\), i.e. \(A_{n''} = \epsilon _2^3 A_{n'} = (\epsilon _1 \epsilon _2)^3 A_n\). Note that \(n''\le \epsilon _2 n'\), hence \(n''\le \epsilon _1\epsilon _2 n\), but still \(\epsilon ^2 - \epsilon _1\epsilon _2\) is rather small, and all squares larger than \(\epsilon _1\epsilon _2 n\) are already packed.

In this phase \(1^{\circ }\) remains valid, and the following analogues of \(2^{\circ }\)–\(3^{\circ }\)–\(4^{\circ }\) can be observed.

\(5^{\circ }\):

The number of squares packed in any vertical slice is \(O(\epsilon \sqrt{n})\), and the number of vertical slices is \(O(\frac{1}{\epsilon }\sqrt{n})\).

Proof

A slice is packed to \(\epsilon _1^3 N_2\) or slightly beyond, and all squares are larger than \(n''\approx \epsilon _1\epsilon _2 n\), while the largest square is \(n'\le \epsilon _1 n\). Therefore the number of squares in a slice is least \(\approx 2\epsilon ^2 N_2/n\) and at most \(\approx 2\epsilon N_2/n\). Fewer than \(\epsilon n\) squares are packed in this phase, hence the number of slices does not exceed \(\approx \frac{1}{2\epsilon } \frac{n^2}{N_2} = O(\frac{1}{\epsilon }\sqrt{n})\). \(\square \)

\(6^{\circ }\) :

The largest horizontal gap inside a vertical slice is O(1).

Proof

Let again \(a_i\) and \(b_i\) denote the size of the smallest and the largest square in an arbitrarily chosen vertical slice. Now we have \(a_i \gtrsim \epsilon ^2 n\) and \(b_i = a_i+O(\epsilon \sqrt{n})\). Since the slice is packed to \(\epsilon _1^3 N_2\), the gap can be estimated from above with

$$\begin{aligned} \frac{\epsilon _1^3 N_2}{a_i} - \frac{\epsilon _1^3 N_2}{b_i} = \epsilon _1^3 N_2 \, \frac{b_i-a_i}{a_ib_i} \approx \epsilon _1^3 \, \frac{\Theta (n\sqrt{n})\, O(\epsilon \sqrt{n})}{\epsilon ^4 n^2} = O(1) . \end{aligned}$$

This upper bound does not depend on \(\epsilon \). Consequently the blank area inside each vertical slice is \(O(\epsilon ^3N_2)\). \(\square \)

\(7^{\circ }\) :

The total width of the vertical slices is at most \((1-\epsilon _2^3) N_1 + O(\frac{1}{\epsilon }\sqrt{n})\).

Proof

The area of squares packed during Phase 2 is \(A_{n'}-A_{n''} = \epsilon _1^3 (1-\epsilon _2^3) N_1 N_2\), moreover by \(5^{\circ }\) we have \(O(\frac{1}{\epsilon }\sqrt{n})\) slices with \(O(\epsilon ^3N_2)\) blank area in each, hence the total blank area is \(O(\epsilon ^2 N_2\sqrt{n})\). Since the totally packed height is at least \(\epsilon _1^3N_2\), the assertion follows. \(\square \)

If \(\epsilon \) is very small and n is not too large, it may be technically complicated to separate the \(O(\frac{1}{\epsilon }\sqrt{n})\) term from n. This situation can be handled by packing no vertical slices beyond \(O(\frac{1}{\epsilon }\sqrt{n})\), turning the rest to horizontal position and placing them on the top of the additional slice of Phase 1. The term \(O(\frac{1}{\epsilon ^3} \sqrt{n})\) then swallows the current \(O(\frac{1}{\epsilon }\sqrt{n})\).

After these two phases an \((\epsilon _2^3 N_1 + n) \times (\epsilon _1^3 N_2 + \epsilon n)\) rectangle remains blank. Apart from an additional lower-order height, it is more than enough for the packing of the squares not larger than \(\epsilon _1 \epsilon _2 n\), by a repeated application of such alternating horizontal/vertical phases whose number is at most \(\lceil \log _{1/\epsilon } n \rceil \). For the necessary extra height, say h(n), we obtain the following recursion:

$$\begin{aligned} h(n) \le h(\epsilon ^2 n) + O\Bigl (\frac{1}{\epsilon ^3} \sqrt{n}\Bigr ) . \end{aligned}$$

This yields \(h(n) \le C'(\epsilon ,c) \sqrt{n}\) for a suitable constant \(C'(\epsilon ,c)\).

4 Concluding remarks

We have proved that the squares of sizes \(1,2,\dots ,n\) can be packed with guillotine-type cuts into a square of size \(\sqrt{1^2+2^2+\cdots +n^2}+cn\), where \(c<1\) is a constant. The calculation yielding \(c\le 7/8\) offers the possibility of obtaining slightly better bounds, for example by applying the following ideas:

  • In Case (b), i.e. \(N_1 > N_2-H\) in the proof of Theorem 4, the coefficient of the major term \(nN_1\) is positive not only for \(c\ge 3/4\) but also for all \(c>21/32\), and for large n it dominates the lower-order negative term of \(\Theta (n^2)\). This improves the upper bound for guillotine-cuts.

  • Instead of \(N_1+n\) on the horizontal side one may take \(N_1+cn\) where c is not very small but smaller than 1. Although this does not guarantee complete packing to \(N_1\) or beyond in the first few rectangles, the rectangles containing squares not larger than \(\lfloor cn \rfloor \) can be overpacked and so compensate for the loss in rectangles of small indices. This improves the bounds in both types of packings.

However, for the sake of keeping this note short and not very technical, we did not intend to decrease the upper bounds given in our theorems to the limits of these methods.