Spatially constrained adaptive rewiring in cortical networks creates spatially modular small world architectures

Abstract

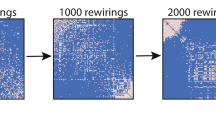
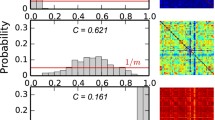
A modular small-world topology in functional and anatomical networks of the cortex is eminently suitable as an information processing architecture. This structure was shown in model studies to arise adaptively; it emerges through rewiring of network connections according to patterns of synchrony in ongoing oscillatory neural activity. However, in order to improve the applicability of such models to the cortex, spatial characteristics of cortical connectivity need to be respected, which were previously neglected. For this purpose we consider networks endowed with a metric by embedding them into a physical space. We provide an adaptive rewiring model with a spatial distance function and a corresponding spatially local rewiring bias. The spatially constrained adaptive rewiring principle is able to steer the evolving network topology to small world status, even more consistently so than without spatial constraints. Locally biased adaptive rewiring results in a spatial layout of the connectivity structure, in which topologically segregated modules correspond to spatially segregated regions, and these regions are linked by long-range connections. The principle of locally biased adaptive rewiring, thus, may explain both the topological connectivity structure and spatial distribution of connections between neuronal units in a large-scale cortical architecture.

Appendices

Appendix 1: Evenly distributed points on a sphere

There does not yet exist a solution to evenly distribute points on a sphere for any number of points.

We thus devised the following iterative algorithm to approximate an even distribution of 500 points on the sphere.

• Step 0: Initialise points at positions drawn randomly from a uniform distribution on the unit sphere, with coordinate vectors $\mathbf {x}_i\in \mathbb {R}^{3}$, $i=1,\ldots ,n$, and $\Vert \mathbf {x}_{i}\Vert =1$.

• Step 1: Define the crowdedness around a point $i$ as $K_{i}=(\sum _{j\ne i} \Vert \mathbf {x}_{i}-\mathbf {x}_{j} \Vert )^{-1}$. Choose the most crowded point $j$ such that $K_{j}=\max _{i}{K_{i}}$.

• Step 2: Given point $j$, each other point $k$ moves away from $j$ in the direction of the vector $\mathbf {x}_{k}-\mathbf {x}_{j}$, by an amount determined by a linearly dampening function

  $$\begin{aligned} F_{jk}=\frac{\alpha }{c}\exp {( -\beta \Vert \mathbf {x}_{j}-\mathbf {x}_{k}\Vert )} \end{aligned}$$

  where $\beta =5$ determines how $F_{jk}$ decreases over distance; large $\beta$ means repelling force acts over a small spatial distance and vice versa. A systematic trial and error search found $\beta =5$ to be most successful. The dampening coefficient $\alpha$ decreases linearly with $\alpha (t)=1-\frac{t}{T}$ for $t=0,\ldots ,T-1$. The coefficient $c=\sqrt{\frac{n}{2}} \max _{k\ne j}{\left( \exp ^{\left( -\beta \Vert \mathbf {x}_{j}-\mathbf {x}_{k}\Vert _{1}\right) }\right) }$ normalises $F$ so that $F\in \left( 0,\alpha \sqrt{\frac{2}{n}}\right)$, where $\frac{2}{\sqrt{n}}$ is the approximate distance between nearest neighbours among an evenly distributed set of points on the sphere.

• Step 3: Project each point back onto the sphere: $\frac{\mathbf {x}_{k}-\mathbf {x}_{j}}{\Vert \mathbf {x}_{k}\Vert }$.

• Step 4: Repeat from Step 1 until $\frac{n(n-1)}{2}$ iterates have been reached.

For a set of finitely many evenly distributed points on the sphere, the cumulative number of points when moving in the azimuthal angle is a discrete approximation to the surface integral with respect to the azimuthal angle. Thus, we measure the accuracy of the approximated even distribution of points on the sphere as the absolute error between the cumulative number of points (normalised to unity) and the surface integral (normalised to unity). This is calculated for each point. Figure 14 shows the average value of absolute error for all points at the same azimuthal angle as a function of azimuthal angle.

We see in Fig. 14 that the average absolute error is always less than 0.35 %. Since $n=500$, a 0.4 % error is equal to $\frac{2}{n}$ and hence corresponds to approximately 2 points more or less than the expected cumulative number of points at any given azimuthal angle given a uniform distribution.

Fig. 14

Average value of absolute error between the cumulative number of points (normalised to unity) and the surface integral (normalised to unity) as a function of azimuthal angle

Appendix 2: Network measures

Measures of clustering coefficient, average shortest path length, weighted clustering coefficient, and edge betweenness are taken from (Rubinov and Sporns 2010).

Clustering coefficient

Let $a_{ij}$ be the entries of the adjacency matrix, i.e. $a_{ij}=1$ if $i$ connects to $j$, and $a_{ij}=0$ otherwise. The degree of a node with undirected connections is calculated as

$$\begin{aligned} k_{i}=\sum _{j=1}^{n}a_{ij}. \end{aligned}$$

The number of triangles pivoting on node $i$—pair nodes adjacent to node $i$ that are themselves connected—is calculated as

$$\begin{aligned} t_{i}=\frac{1}{2}\sum _{j,h\in \mathcal {N}}a_{ij}a_{ih}a_{jh}. \end{aligned}$$

Thus the clustering coefficient can be determined as,

$$\begin{aligned} C=\frac{1}{n}\sum _{i\in \mathcal {N}}C_{i}=\frac{1}{n}\sum _{i\in \mathcal {N}}\frac{2t_{i}}{k_{i}(k_{i}-1)} \end{aligned}$$

(2)

Average shortest path length

A path of length $l$ between nodes $i$ and $j$ is a sequence of vertices $\eta _{i\leftrightarrow j}=(i=i_0,\ldots ,i_l=j)$ with $a_{i_{k,k+1}}=1$. Let $l_{ij}$ be the length of the shortest path between $i$ and $j$. The average shortest path length is the mean value over all pairwise nodes, calculated as

$$\begin{aligned} L=\frac{1}{n(n-1)}\sum _{i\in \mathcal {N}}\sum _{j\in \mathcal {N}_{i}}l_{ij}. \end{aligned}$$

(3)

For disconnected pairs of nodes $l_{ij}$ is undefined, however, such pairs are excluded in the MATLAB program computation to allow a result.

Modularity

Let $\Theta =\lbrace \theta _1,\theta _2,\ldots \rbrace$ be a partition of the nodes of the network into modules, i.e. the subsets of nodes that form non-overlapping communities. Let $\Pi _{\theta _i\theta _j}$ denote the fraction of all edges in the network that connect nodes in module $\theta _i$ to nodes in module $\theta _j$. Then the modularity for this set of modules is calculated as

$$\begin{aligned} Q=\sum _{\theta _i\in \Theta }\left[ \Pi _{\theta _i\theta _i}-\left( \sum _{\theta _j\in \Theta }\Pi _{\theta _i\theta _j}\right) ^{2}\right] . \end{aligned}$$

(4)

Edge betweenness centrality

Calculated for each edge as the fraction of shortest paths in the network which pass through the edge. Let $H_{uv}$ be the number of shortest paths that connect nodes $u$ and $v$, and let $H_{uv}(i,j)$ be the number of shortest paths between nodes $u$ and $v$ that includes the edge between $i$ and $j$.

Then, the edge betweenness value for the edge between $i$ and $j$ is calculated as

$$\begin{aligned} \mathrm {EB} = \sum _{\begin{array}{c} u,v\in \mathcal {N}\\ u\ne v\\ \end{array}}\frac{H_{uv}(i,j)}{H_{uv}}. \end{aligned}$$

(5)

Small-worldness

Calculated as the normalised ratio of the clustering coefficient to the average shortest path length:

$$\begin{aligned} \Sigma =\frac{C/C_{\text {rand}}}{L/L_{\text {rand}}}, \end{aligned}$$

(6)

for $C$ the clustering coefficient and $L$ average shortest path length of a network, normalised respectively by the corresponding quantities $C_{\text {rand}}$ and $L_{\text {rand}}$ for a corresponding random network.

Weighted clustering coefficient

A weighted triangle is determined as the cubic root of the product of the three weighted edges that make a triangle centred on a given node. The sum of all triangles pivoting on a given node $i$ is

$$\begin{aligned} t_{i}^{w}=\frac{1}{2}\sum _{j,h\in \mathcal {N}}{(w_{ij}w_{ih}w_{jh})}^{1/3} \end{aligned}$$

for edge weights $w_{ij}$, defined by the linear relation

$$\begin{aligned} w_{ij}=\left\{ \begin{array}{ll} 1-\frac{d_{ij}}{\pi } &{} \text { if }\quad a_{ij}=1 \\ 0 &{} \text { otherwise} \end{array}\right. \end{aligned}$$

Zero distance corresponds to a weight of 1 and the maximum distance $\pi$ corresponds to a zero weight. Thus, the weighted clustering coefficient is calculated as

$$\begin{aligned} C^{w}=\frac{1}{n} \sum _{i\in \mathcal {N}} {C_{i}^{w}} = \frac{1}{n} \sum _{i\in \mathcal {N}} \frac{\sum _{j,h\in \mathcal {N}}2t_{i}^{w}}{k_{i}(k_{i}-1)} \end{aligned}$$

(7)

Network wiring cost

The normalised average edge length for all edges of the network is

$$\begin{aligned} M=\frac{1}{\pi \sum _{i\in \mathcal {N}}{k_{i}}}\sum _{i\in \mathcal {N}}\sum _{j\in \mathcal {N}_{i}}{d_{ij}}, \end{aligned}$$

(8)

where $\pi$ is the maximum edge length that connects two nodes on the shortest arc along the great circle for the network embedded on a unit sphere. A network wiring cost value of 1 indicates an average edge length of $\pi$, of zero indicates an average edge length of zero, and of $\frac{1}{2}$ indicates the expected value for randomly distributed edge lengths.