1 Lunar ISRU and the need for small scale lunar excavation devices

The Moon will provide future in situ resource utilisation (ISRU) missions with a valuable feedstock in form of its powdered surface layer of soil–the lunar regolith. This material is formed from a mixture of lunar rock and minerals with an added exogenically component introduced by various mechanisms: solar wind particles [35], asteroidal material, and cometary material [24, 27, 37]. The regolith, thus, contains a diverse range of chemical elements, which may be valuable reserves for a range of industrial and exploration applications [6, 11]. Therefore, access and extraction of the regolith are widely regarded as a key enabler of a future lunar economy and permanent human presence [11, 19, 34, 41, 42, 46], which will also enable a wide range of lunar science applications [10, 14, 16, 17, 26, 27].

At the beginning of the ISRU process chain, the geological material has to be excavated and moved to a local collection point [23, 30], and subsequently beneficiated. For early ISRU applications, that are, lunar soil particles are sorted into appropriately sized components [40]. However, the efficient and reliable excavation of regolith on the lunar surface present a significant challenge that must be overcome before lunar ISRU becomes a viable endeavour.

During the Apollo missions, all regolith samples were acquired by astronauts using human-operated surface sampling tools (scrapers, rakes, tongs, etc.) and sub-surface sampling tools (drills, core tubes, etc.) [4], where drilling was reported as a challenging task [50]. Working in the Moon’s reduced gravity environment has a notable effect on the excavator mass required for successful extraction of the regolith [53]. On Earth, moving soil in large quantities is usually accomplished by heavy industrial machinery which utilises extensive amounts of force to achieve the given task. This mass intensity is necessary in order to counteract both lateral and vertical forces during excavation, which otherwise could lead to slipping or lifting of the excavator [53]. Given that the mass of a vehicle has a substantial effect on the available traction force and that increasing the mass of a lunar excavator would imply significant financial penalties due to increased launch costs [7], the design of lunar excavators must regard the minimisation of excavation forces as a top priority; especially for early ISRU missions involving small excavators. In a study presented by Wilkinson and DeGennaro [51], the maximum effective tractive force (defined as the difference between motion resistance and soil thrust) of the roughly 700 kg Apollo Lunar Roving Vehicle (LRV) was calculated as a mere 239 N on the Moon. Using the same soil parameters and calculations as used by Wilkinson and DeGennaro [51], Fig. 1 shows an estimation of the available effective traction force of other flown planetary rovers on the lunar surface.Footnote 1 In order for a vehicle to be able to excavate material successfully, the available effective tractive force has to be multiple times larger than the necessary excavation force [18].

Fig. 1
figure 1

Estimation of available effective tractive force for different planetary rovers in the lunar environment. Calculations and soil data can be found in [51]. Available tractive force is based on overall system mass and ground vehicle friction parameters (such as grousers. Grousers = Devices to increase track traction, such as protrusions) are not considered. Both lunar (LRV, Lunokhod, LUVMI-X; grey markers) and martian (Sojourner, Spirit, Opportunity, Curiosity, Perseverance; orange markers) rovers are plotted for comparison

Full size image

Thus, for excavation on planetary bodies with a reduced influence of gravity, means to reduce the necessary excavation forces must be investigated. Besides the optimisation of the cutting surface geometry, previous studies have shown that the utilisation of vibration or percussion can drastically decrease the necessary excavation forces, reaching up to a 40-times reduction in required force [9, 15, 22, 39, 44, 48, 52]. This is relevant for a lunar ISRU use-case, as a reduction in excavation forces translates directly into a possible reduction of vehicle mass or will allow the mechanism to be deployed on a smaller vehicle, which can lead to an increase in launch opportunities. Other researchers have investigated the use of vibration or electrostatics to acquire and/or convey regolith, as well as to reduce penetration forces [1, 31,32,33]; such techniques are not further considered in the present study as solely the decrease in excavation forces was of interest. Integrating vibrating mechanisms increases the power requirements of a given system, the potential increased rate of material fatigue must be considered, and sensitive scientific instruments must be protected accordingly. However, if significant mass savings can be achieved, the above concerns are far outweighed by the benefits.

Previous studies have investigated the effect of vibrations or more often, percussions, on discrete excavation devices (for a discussion of discrete and continuous excavators, see [30]) that push soil (i.e. bulldozing) or take one large charge at a time. To expand these approaches, this proof-of-concept study investigates four different leading-edge geometries, tests the forces necessary to excavate at different digging depths, angles, and speeds and investigates what force reductions can be achieved by utilising vibration. While a flat blade has been employed as a reference experiment (Figs. 3 and 4), the investigated leading-edge shapes are not designed to act as the actual excavation mechanism themselves (as would be the case for a discrete excavator operating in batch-mode), but rather to act as a leading-edge or an inlet interacting with the soil for use with a continuous conveying device behind them; for instance, an auger, conveyer belt, or similar technologies. The aim is to cut through the soil, lift the material of the ground with as little force as possible, and to guide it towards the back of the device where it would be transported away by a secondary conveying mechanism. For a more detailed discussion of different excavation methods and the concept of discrete and continuous excavator can be found in [30]. Such inlet shapes could be easily combined with sieves or meshes to enable the rejection of coarse particles to help beneficiation and to also mitigate the risks caused by larger rock fragments for the regolith transportation system. The decision of which leading-edge geometries to test has been based on different concepts used in terrestrial applications, such as agriculture or road clearing. It is important to highlight that the present blade shapes are not designed based on a specific set of mission requirements or for one specific excavation task, but rather aim to investigate a wide range of possible extractor designs in the present proof-of-concept study.

Small lightweight lunar robotic vehicles are currently under development, which are most likely the first candidates for carrying lunar excavation systems, for example, the LUVMI and LUVMI-X rover platforms [20, 29]. These vehicles are not designed to provide significant effective traction force, and so we have chosen to focus the test campaign towards designing a tool that can excavate the top few centimetres of soil. It is advantageous to focus on the readily powdered top centimetres of soil for ISRU applications that solely require the bulk regolith material, such as additive manufacturing [21, 55] or certain oxygen extraction methods as for instance the FFC-Metalysis process [36], unlike other processes that require specific minerals like, for example, ilmenite for hydrogen reduction [43]. In the following, the experimental setup as well as the investigated shapes are discussed in more detail. Several studies have focussed on the mathematical modelling of necessary excavation forces [51, 53], but since most analytical models are based on specific geometric simplifications, predicting the required forces of more complex shapes is challenging. Discrete element simulation software capable of simulating solid particles, such as EDEMFootnote 2 or Rocky DEM,Footnote 3 can be applied to overcome this limitation. However, due to the small average particle size of around 72 µm for lunar regolith [12, 49] and the wide particle size distribution from dust to cm size particles, millions of particles must be simulated, resulting in a significant demand for computing power as well as computational time. Additionally, in advance of such simulations, experimental data are necessary to calibrate the models [8]. Thus, an empirical approach is presented in this paper, serving as a proof-of-concept for the effect of leading-edge geometry on excavation forces of small-scale continuous lunar excavators and their reduction through design and application of vibration.

2 Experimental setup and test methods

2.1 Regolith analogue test bed

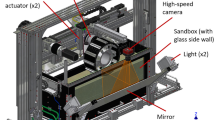
The test bed setup at the University of Manchester (UoM) is based on an acrylic box with inner dimensions of 100 × 60 × 30 cm. The setup is depicted in Fig. 2 and is filled with 150 kg of UoM-B lunar regolith analogue material (Fig. 2–feature a); for a full characterisation of the analogue, see [28]. The material was compacted to a filling level of 18 cm, resulting in an in situ density of roughly 1.6 g/cm3, similar to that of lunar regolith [13]. After each experiment, the soil was loosened with a rake and re-compacted to this filling level with a flat blade. Since only small excavation devices are to be tested with this arrangement, a box width of 60 cm is sufficient to avoid boundary effects, recognised as approximately three times the width of the tested implements. The same is valid for the depth of the analogue material, as cutting depths only reach up to a maximum of 5 cm [2].

Fig. 2
figure 2

An image of the experimental setup showing the box filled with lunar analogue UoM-B (a). Features on the setup include: the support structure (b), the linear bearings and their covers (c), the guiding rails (d), the linear actuator (e) and its fixtures (f), the loadcell for horizontal excavation forces (g), the loadcells for vertical excavation forces (h), the height adjustment mechanism (i), and the lockable hinges for the cutting angle adjustment (j). Here, a flat blade is attached

Full size image

A support structure (Fig. 2–feature b) for the excavation tool consists of aluminium profiles and an aluminium top shelf, connected to two housings for two linear ball bearings (Fig. 2–feature c) each, which allow the structure to slide along the rails (Fig. 2–feature d) with minimal friction while maintaining the correct orientation of the experiment even during heavy loads. The support structure is pushed along the rails with the help of a 12-V DC linear actuator (Fig. 2–feature e; Gimson Robotics GLA600-S) with a maximum stroke of 700 mm and a maximum no-load speed of 21 mm/sec. The actuator is powered by an external power supply and controlled using a microcontroller and motor driver. The actuator is connected to the experiment structure with two aluminium brackets (Fig. 2–feature f; Gimson Robotics) to prevent any movement during operation. It exerts force onto a button load cell (Fig. 2–feature g; 50 kg, Phidgets) housed in a 3D-printed PLA (polylactic acid) adapter while pushing the sledge along (horizontal excavation force). The connection point for the excavation implements includes two beam load cells (Fig. 2–feature h; 50 kg, Phidgets) to be able to monitor vertical excavation forces and includes a mechanism to adjust the digging depth (i). Additionally, the digging angle can be adjusted by means of two lockable hinges (Fig. 2–feature j); digging angles were verified with a digital inclinometer before each experiment. All three load cells are connected to HX711 signal amplifiers and the microcontroller.

An ultrasonic range finder (HC-SR04) is included in the setup, which measures the extension of the actuator, and therefore, the distance the excavation implement was pushed through the soil in each experiment. At a pre-defined distance, the experiment stopped automatically to ensure repeatable experiment runs and to prevent interference of the blade with the containment. All data were recorded at a frequency of 2 Hz, and all load cells were calibrated with precision weights prior to use. To investigate the effect of vibration, a 20-mm eccentric mass vibration motor (Precision Microdrives 320–105) was attached above the digging implement and operated at 2 V, which translates to a vibration amplitude of around 3.25 g and a frequency of 75 Hz. This setting was chosen since it is well within the envelope of the motor, allowing operation for extended periods of time, as well as due to its relative acceleration, which is calculated by \(\Gamma = \frac{applied\;vibrational\;acceleration}{ambient\;acceleration}\) and therefore results in a Γ of 3.25 here. The higher this value in general, the more fluidized the soil becomes. The orientation of the vibration motor can be seen, for instance, in feature E of Fig. 5. It creates mixed-mode vibrations in all directions, with the maximum amplitude being created along the x-axis (see Fig. 2 for coordinate system). It is important to note that the inclusion of vibration serves as a proof-of-concept in the present study. The specific excitation and mode imposed onto the cutting implement is domain dependent, i.e. the size, shape, mass, and material. Additionally, the imposed excitation will vary with the accumulation of soil during each experiment, as increased charges will dampen overall amplitude and eliminate higher harmonics. However, the tested shapes were not developed for one specific application and thus investigations as well as optimisations of the vibration modes, resonance frequencies, vibrational magnitudes, and frequencies of each implement lie outside the feasible scope of this initial investigation. Similar proof-of-concept studies have previously been performed by other workers, such as [9, 15], or [53], which differ to that presented here in that only one specific system or geometry was tested and that no comparisons across different geometries in the same operating conditions are drawn. Even though the presented approach does not test all possible characteristics or provide a complete vibrational analysis, it does create an initial framework from which conclusions can be drawn and design parameters for future prototypes can be derived. Therefore, the optimisation of frequency and amplitude will be the subject of future work.

2.2 Investigated geometric shapes and experiment parameters

A total of 56 discrete experiments were performed, considering 4 different inlet geometries; all experiment runs are listed in Tables 1 and 2, which also report the maximum reported excavation forces per run, both horizontally as well as vertically. A flat AA 6083 aluminium alloy blade (150 mm × 80 mm × 3 mm; Figs. 2 and 3) was used to obtain reference measurements and to test the functionality of the setup. Subsequent tests used two bucket shapes with an opening angle of 0° and 15°, respectively (100 × 80 mm for 0°; 124 × 80 mm for 15°; 3D-printed PLA; Fig. 3). As previously mentioned, the shapes are intended to act as a leading edge/inlet for a secondary conveying mechanism; therefore, the same length was chosen over the same width for the angled buckets. The final leading-edge shape tested was a cylindrical shape (50 mm inner diameter; 80 mm length; 3D-printed PLA; Fig. 3), inspired by widely used geometries for garden shovels or plow blades used in agriculture. Even though the flat blade is made from a different materials than the other geometries, due to ease of manufacture, which will of course affect the interaction between soil and material; this difference is negligible in the given circumstances. The aim is not to investigate the soil–material interaction directly at their contact point or the wear behaviour of the blades, but rather the surcharge characteristics and induced excavation forces. These are influenced more drastically by the geometry, rather than by the difference in surface roughness of two relatively smooth materials. All shapes can be seen next to each other in Fig. 3. All geometries, except the flat blade, are open at the back, as described in Sect. 2, since they are intended to be used with a secondary soil transport mechanism. The ideal outcome is reaching a force equilibrium, where the excavation forces stay relatively constant due to the material exiting the mechanism. In this case, a lunar excavator could operate continuously for extended periods of time without the need of breaking contact with the soil, and thus resulting in higher excavation rates. Terrestrially, excavator leading edges are often equipped with teeth to facilitate excavation; such features could be beneficial, as discussed in [25] but were not included in the present study due to the focus on excavation forces caused by different geometries.

Table 1 Overview of all performed laboratory experiment runs including the maximum recorded horizontal excavation forces
Full size table
Table 2 Overview of all performed laboratory experiment runs including the maximum recorded vertical excavation forces
Full size table
Fig. 3
figure 3

Overview of the tested geometries. a flat blade; aluminium; b straight bucket blade; PLA; c open bucket blade; PLA; d cylindrical blade; PLA. The narrow slot is used for attachment to experimental setup. The top and bottom panels in the figure show slightly different views of the blades to illustrate their back opening

Full size image

The digging depth was adjusted in 1 cm steps with cuts at 3 to 4 cm already resulting in the flat blade getting stuck in the soil, leading to a sharp increase in excavation forces which could eventually damage the actuator or other components. Some experiments exceeded horizontal excavation forces of 200 N, which given the small size of the tested geometries and the shallow digging depths, is excessive (see Table 1 for an example of this). For a lunar rover, such forces could have catastrophic consequences, as the momentum on the rover would be significant and could lead to it tipping over, resulting in mission failure. Thus, except for two experimental runs, only digging depths up to 3 cm are considered here. Two different cutting angles were investigated, namely 15° and 30°, measured against the horizontal plane of the soil surface. Lastly, runs were performed at different actuator speeds of 10 mm/sec and 5 mm/sec, as well as with and without vibration. During the experiments, the digging implements travelled approximately 41 cm though the soil.

3 Results

Tables 1 and 2 show an overview of all performed experiment runs, where experiments with excavation forces exceeding the safe limits due to the digging implement getting stuck in the soil are greyed out.

The initial experiments with the flat blade were performed up to 4 cm digging depth, but it became apparent that the deepest cuts already lead to immense forces acting on the excavation implement. Thus, this depth was not tested for the other bucket shapes as similar results would have been expected; therefore, these are labelled “N.A.” in Tables 1 and 2. Before each set of experiments, a reference run was performed with and without vibration (no contact to the soil, but with the same configuration in terms of angle and speed). The required forces for these runs, representing the force necessary to overcome the friction in the system, was subsequently subtracted from the force curve of runs with soil contact. Therefore, the forces evaluated below represent the actual forces induced by the excavation operation and are independent of the friction of the system.

3.1 Flat blade

Figures 4, 6, 7, and 8 show the recorded excavation forces for the different runs at different digging depths. Experiments without the use of vibration are shown in solid lines and dashed lines indicate the use of vibration. These figures show a 3-step moving average of the raw data, which can be found in the supplementary information to this publication. The bar charts shown indicate the change in necessary excavation forces, both horizontally as well as vertically, when utilising vibration. The percentage change was calculated by computing the area below the force-time curves, which are reported across identical time spans. Comparing these values allows for a comparison of the overall force required for the whole run. This, combined with the reported peak forces in Tables 1 and 2, gives a valid indication of the required overall forces.

Fig. 4
figure 4

Recorded horizontal (a) and vertical (b) excavation forces for the flat blade at 15° cutting angle and a cutting speed of 5 mm/sec. The bar chart (c) shows the change in necessary forces when using vibration. Raw data reported in supplementary Figure S1

Full size image

Our results (Fig. 4, Tables 1 and 2) show that the use of vibration reduces the horizontal excavation force significantly, up to around 30% for a shallow cut at 1 cm. This decrease in required force becomes less significant with increasing digging depth; however, the reduction is still noteworthy. The use of vibration delays the rise in horizontal excavation forces, as the surcharge is hindered from piling up due to material flowing more easily, which becomes more apparent at increased digging depths. Interestingly, the required horizontal excavation force at 4 cm depth with vibration surpasses the one without at a certain point, which could be caused by the increasing surcharge mass acting as a damper for the vibration or changing the vibration mode, and thus preventing any further force reduction. For detailed discussions of the soil mechanics involved in the creation of surcharges, see [3, 38, 54]. Regarding the vertical excavation forces, vibration do not significantly decrease the required forces. For deeper cuts (3 to 4 cm), the vertical excavation force even increases with the use of vibration, as the surcharge is compacted by the effects of the vibration. The cyclic behaviour visible for both excavation forces, which becomes more apparent for deeper cuts (3 to 4 cm), is caused by the surcharge piling up (increase in force) and then suddenly breaking loose and moving forwards (decrease in force). A similar behaviour can be observed in most of the data in the following. Some of these described phenomena can be seen in Fig. 5, showing images of the surcharge after the described test at digging depths of 1 to 3 cm, with (A–C) and without (D–F) vibration.

Fig. 5
figure 5

Images of the surcharge after experiments with a flat blade at 15° cutting angle and at 5 mm/sec. A 1 cm, no vibration; B 2 cm, no vibration; C 3 cm, no vibration; D 1 cm, vibration; E 2 cm, vibration; F 3 cm, vibration

Full size image

As the excavation speed was increased (Fig. 6), a primary observation is that a cut at 4 cm depth with the use of vibration resulted in the blade getting stuck (see Tables 1 and 2). This is a result of the already high horizontal excavation force of around 85 N and the increase in vertical excavation force with vibration, as shown above. This combination leads to the blade changing its cutting angle due to the significant momentum acting on it, which in turn makes the problem even more severe as the cutting angle increases. Overall, the maximum required forces for cuts up to 2 cm are lower compared to a slower cut at the same angle and almost similar at deeper cuts. The use of vibration again reduces the horizontal excavation force but increases the vertical excavation forces at deeper cuts. The decrease in the horizontal excavation force for a shallow 1 cm cut is significant, as it almost halves the required overall force.

Fig. 6
figure 6

Recorded horizontal (a) and vertical (b) excavation forces for the flat blade at 15° cutting angle and a cutting speed of 10 mm/sec. The bar chart (c) shows the change in necessary forces when using vibration. Raw data reported in supplementary Figure S2

Full size image

Figure 7 shows the results for an increased cutting angle of 30°. Overall, the required horizontal excavation force increases compared to the same speed at a lower cutting angle and cuts at 4 cm are not possible at all anymore. Since the blade angle is now steeper, the blade cuts less well through the soil but rather displays a pushing or plowing motion, leading to a steep increase in the required force and would therefore exert a significant momentum on any vehicle. Vibration reduces the required horizontal excavation force significantly, even more than at a slower speed (Tables 1 and 2). Overall, a decrease in required vertical excavation force can be observed compared to the same speed at 15°, as less soil accumulates on top of the blade. This is caused both by the steeper blade angle as well as the pushing motion that lofts less material off the ground.

Fig. 7
figure 7

Recorded horizontal (a) and vertical (b) excavation forces for the flat blade at 30° cutting angle and a cutting speed of 5 mm/sec. The bar chart (c) shows the change in necessary forces when using vibration. Raw data reported in supplementary Figure S3

Full size image

Similar observations can be made for a cut at a high angle and with a higher speed (Fig. 8). Here, already a 3 cm cut without the use of vibration is not possible anymore and the forces are significantly higher than for both the same digging angle at slower speeds, as well as the same speed at a lower cutting angle. Nevertheless, the use of vibration decreases the necessary horizontal excavation forces but increases the vertical excavation forces; this is consistent with the observations from the runs described above.

Fig. 8
figure 8

Recorded horizontal (a) and vertical (b) excavation forces for the flat blade at 30° cutting angle and a cutting speed of 10 mm/sec. The bar chart (c) shows the change in necessary forces when using vibration. Raw data reported in supplementary Figure S4

Full size image

In summary, our findings suggest that shallow cuts (1 to 2 cm) at a low cutting angle (15°) with a slightly increased excavation speed (10 mm/sec) result in the lowest overall excavation forces. The effects of using vibration to reduce excavation forces are significant (up to 50% force reduction), and therefore, are worth the increased demand in power. It is apparent that steep cutting angles (30°), even with the use of vibration, are detrimental for the given use case as they increase the necessary forces and additionally increase the risk of the digging implement getting stuck in the soil. Taking these findings into consideration, all of our remaining experiments were performed at a cutting angle of 15°. The high overall excavation forces for even a very small digging implement and relatively shallow cuts, which increase linearly with the digging depth, show that discrete excavation with a flat blade or bulldozing does not seem applicable for a lunar use case where low excavation forces are critical.

3.2 Straight bucket blade (0° opening)

Figure 9 shows the results for the straight bucket (as depicted in Fig. 3b) at a 15° cutting angle and for a speed of 5 mm/sec, and Fig. 10 shows the same shape at a speed of 10 mm/sec (data are reported in Tables 1 & 2). Overall, the peak forces for this shape are significantly lower than for a flat blade. We attribute this to the shape cutting through the soil more easily, thus reducing the surcharge mass, reduced width, as well as a reduced surcharge mass as the material is allowed to leave the excavation implement easily (Fig. 3b). The latter starts to take an effect from 2 cm digging depth, as there is not enough material excavated at 1 cm to reach the end of the geometry. Vibration increases the amount of material exiting the geometry as it increases the flowability of the soil. As previously mentioned, ideally the force curve would level off and stay relatively constant. Even though this equilibrium of forces is not reached here yet, it is visible in Fig. 10 that the required force is starting to level out once enough material exits the mechanism. This is especially apparent in the recorded values for the vertical excavation forces. While vibration again helps to reduce the horizontal excavation forces significantly, it can be seen that shallow and slightly faster cuts are beneficial, unless deeper cuts are targeted. Deeper cuts, however, seem disadvantageous since it increases the required forces significantly. In general, enough material must be excavated to reach the end of the geometry in order to develop the full force reducing potential of the geometry and to feed the material to the secondary mechanism. This makes a trade-off between the amount of excavated material and force required necessary. Two additional verification runs were performed at a 5° cutting angle and one at 15 mm/sec, which both resulted in additional force reductions. Because of this clear relationship between angle, speed, and required force, subsequent experiments were performed at a 15° cutting angle and a speed of 10 mm/sec to allow for a good comparison to prior results utilising the flat blade.

Fig. 9
figure 9

Recorded horizontal (a) and vertical (b) excavation forces for the straight bucket at 15° cutting angle and a cutting speed of 5 mm/sec. The bar chart (c) shows the change in necessary forces when using vibration. Raw data reported in supplementary Figure S5

Full size image
Fig. 10
figure 10

Recorded horizontal (a) and vertical (b) excavation forces for the straight bucket at 15° cutting angle and a cutting speed of 10 mm/sec. The bar chart (c) shows the change in necessary forces when using vibration. Raw data reported in supplementary Figure S6

Full size image

3.3 Open bucket blade (15° opening)

Figure 11 shows the result for the bucket geometry with an opening angle of 15° (as depicted in Fig. 3c). Generally, the results show a very similar behaviour compared to the bucket with straight walls (Fig. 10). However, more material is piled up in front of the geometry due to the increased projected area of the side walls and thus the required forces are higher overall by 20–30% for the horizontal forces (Table 1) and 10–20% for the vertical forces (Table 2). This emphasises once more that shapes that increase the amount of surcharge produced while excavating must be avoided, even though they would allow for more material being gathered in one cut.

Fig. 11
figure 11

Recorded horizontal (a) and vertical (b) excavation forces for a bucket with 15° opening at 15° cutting angle and a cutting speed of 10 mm/sec. The bar chart (c) shows the change in necessary forces when using vibration. Raw data reported in supplementary Figure S7

Full size image

3.4 Cylindrical blade

Lastly, a cylindrical blade shape (as depicted in Fig. 3d) was tested and the results can be seen in Fig. 12. It is apparent that the peak forces required are significantly lower (up to × 10 compared to the bucket shapes; up to × 11 compared to the flat blade; see Tables 1 and 2) than for any other experimental run, even at an increased cutting depth of 4 cm and that vibration reduce the necessary horizontal excavation force drastically, especially at low digging depths. From a depth of cut of 2 cm onwards, the material begins to reach the end of the geometry and the forces required reach the abovementioned force equilibrium relatively quickly. At 3 cm, the cylinder is almost fully submerged in the soil and would therefore excavate the maximum possible mass. The increase in horizontal excavation force at 4 cm is caused by the geometry being overfilled, thus creating additional contact surfaces between the top of the inlet and the soil.

Fig. 12
figure 12

Recorded horizontal (a) and vertical (b) excavation forces for a cylindrical shaped blade at 15° cutting angle and a cutting speed of 10 mm/sec. The bar chart (c) shows the change in necessary forces when using vibration. Raw data reported in supplementary Figure S8

Full size image

In general, the rounded and narrow shape with a tipped leading edge (Fig. 3d) is by far advantageous compared to more rectangular shapes as it produces almost no surcharge and transports the material off the ground with ease. Even though this is not overly surprising, many proposed lunar excavator designs today utilise buckets or similar rectangular shapes [30]. The digging depth here should be adjusted in a way that the geometry is almost fully submerged in the material to maximise the throughput.

4 Conclusion

In this proof-of-concept study, four different geometric shapes (Fig. 3), representative of possible leading-edge options for lunar excavators with a secondary transport mechanism, have been investigated in a planetary analogue testbed at the University of Manchester. Tests were performed at two different cutting angles, two excavation speeds, and with and without the use of vibration. The presented research shows clearly that shape optimisation of digging implements or excavator inlet geometries for lunar excavation devices must be considered from the beginning of the conceptual design phase. During the performed experiments, horizontal excavation forces varied by more than an order of magnitude between a flat blade and a cylindrical inlet design.

It has been found that bulldozing with a flat blade or a closed bucket is not sensible for lunar applications, where excavation forces must be held to a minimum due to the reduced gravity environment and significant launch costs. The created surcharge causes sharp increases in the necessary forces and even cuts at only a couple of centimetres could not be performed by the robotic vehicles we are utilising today (see Fig. 1); thus, surcharge mass must be kept to a minimum.

Instead of closed blade geometries, the present study shows that lunar excavator designs shall be optimised for the secondary regolith transportation mechanism they are utilising. This can either be achieved with multiple small cutting surfaces that scoop up the soil and store it inside the vehicle, like for instance a bucket wheel excavator as described in [45] or by designing them in a way that excavated material can be transported away from the inlet by an auger, mechanical, or pneumatic conveyer system continuously. This will enable also small robotic vehicles to contribute to the development of future lunar ISRU capabilities. Additionally, multiple shallow cuts at shallow angles should be targeted wherever possible as the necessary forces increase substantially with increasing digging depth and steeper angles. On the lunar surface, this effect will be even more drastic due to the compaction and quickly increasing relative density of the regolith layer [24]. Different inlet geometries will, of course, lead to different excavation mass rates, different surcharge masses, and will affect the required forces differently, which must be considered and optimised for future lunar applications; such investigations are subject of future work as measuring the excavated mass accurately, in situ, and without affecting the excavation forces in a large-scale experiment that focuses on the top few centimetres of the soil is extremely challenging. Therefore, the aim is not to recommend one specific geometry, but rather create a reference framework on which new designs can be based. Thus, the present results demonstrate clear trends across a wide range of possible shapes that should be considered in the design of any excavation implement.

The presented tests were performed under Earth’s gravity and environmental conditions (i.e., pressure) and thus the excavation forces on other celestial bodies or planets will be different, as research indicates that the mechanical behaviour of soils changes in altered gravity conditions [5, 47, 56]. Thus, developments of excavation devices for certain gravitational environments should be complemented with simulations, which allow to change the gravitational acceleration easily, as well as, for instance, parabolic flights for experimental verification.

Critically, applying vibration to cutting edges seems highly beneficial, as the achievable force reduction of up to 50% in the arrangements considered, far outweigh the additional power requirements for excitation. Here, the use of vibration was used as a proof-of-concept, which resulted in significant reductions of necessary forces. However, with optimised vibrational profiles, which are specifically tailored to a specific geometry, implement size, and mass, it is tenable that the required forces could be reduced even further. Such optimisation efforts are only reasonable, however, after a final geometry is chosen for a specific application as slight geometry changes would lead to the need of a full re-characterisation of the vibrational characteristics. In addition, vibration facilitates the clearing of residue material off the cutting surfaces; this is in good accordance with the results reported by, for example, [53].

In the presented experimental study, the omni-directional vibration motor was attached above the cutting implement (as seen in Fig. 5), since different geometries had to be attachable readily, and their cutting angle had to be changed freely. Although the vibration used here acted as a proof-of-concept, for future vibrational actuation of leading edges, we propose the use of linear resonant actuators (LRA), as these allow the direction of vibration in a single axis and thus enable investigations into the optimum vibration direction (horizontal only vs. vertical only vs. combination of both). Additionally, attaching the actuator directly to, or incorporating it into, the chosen leading-edge geometry seems beneficial and simplifies a detailed examination of the vibration mode of the geometry.

In summary, it is found that small robotic soil excavation devices should be equipped with inlets or leading edges that are optimised for the present use-case and environment, and simply miniaturising terrestrial concepts will not be beneficial or not even feasible for many applications. The comparison of the reported forces to the available traction of several robotic vehicles also shows, that we are currently still far away from large-scale excavation endeavours on the lunar surface.