Recovering shear stiffness degradation curves from classification data with a neural network approach

Abstract

Shear stiffness is critical in assessing the stress–strain response of geotechnical infrastructure, and is a complex, nonlinear parameter. Existing methods characterise stiffness degradation as a function of strain and require either bespoke laboratory element tests, or adoption of a curve fitting approach, based on an existing data set of laboratory element tests. If practitioners lack the required soil classification parameters, they are unable to use these curve fitting functions. Within this study, we examine the ability and versatility of an artificial neural network (ANN), in this case a feedforward multilayer perceptron, to predict strain-based stiffness degradation on the data set of element test results and soil classification data that underpins current curve fitting functions. It is shown that the ANN gives similar or better results to the existing curve fitting method when the same parameters are used, but also that the ANN approach enables curves to be recovered with ‘any’ subset of the considered soil classification parameters, providing practitioners with a great versatility to derive a stiffness degradation curve. A user-friendly and freely available graphical calculation app that implements the proposed methodology is also presented.

1 Introduction

1.1 Stiffness nonlinearity, measurement, and prediction

The stress–strain response of soils, regardless of soil type, is typically nonlinear with stiffness modulus varying with strain level and stress path. Although stiffness can be approximated as a constant value for small interval strains, for the strain ranges observed during many geotechnical design problems, there will be meaningful variance in the magnitude of the stiffness modulus [25, 28]. Figure 1 shows a typical stiffness degradation curve [4, 28], annotated with common in situ or laboratory tests and design problems [7]. As such, the ability to predict the change in stiffness with regard to strain, i.e. the stiffness degradation curve, is essential to geotechnical design [4].

Fig. 1

Typical shear stiffness degradation behaviour of soil with strain ranges for several tests and design problems (after [4, 7, 28])

Direct measurement of the stiffness degradation curve can be achieved through a range of laboratory and in situ testing protocols including: resonant column testing [14]; triaxial shear testing [5]; torsional shear testing [43]; and pressuremeter testing [24]. Due to the challenges of retrieving undisturbed samples for laboratory testing and carrying out bespoke element or in situ tests, alongside the importance of stiffness degradation curves in design, the ability to predict such a curve via a small number of soil characterisation parameters would be advantageous. Multiple previous publications demonstrate attempts to define the stiffness degradation curve as a sigmoid (or ‘s’ shaped) function of strain [12, 15, 22]. More recent work has sought further refinement on this concept through the construction of a large data set consisting of many hundreds of individual laboratory tests collected from 61 publications [31].

Empirical analysis and curve fitting using the assembled data set led to the stiffness degradation function described by Eq. (1) [31], where $G$ is the stiffness (secant shear modulus) at strain $\gamma$, ${G}_{0}$ is the elastic stiffness where strain is small, ${\gamma }_{\mathrm{e}}$ is the elastic threshold after which stiffness is no longer assumed to be constant, ${\gamma }_{\mathrm{r}}$ is a reference strain at the point where $G/{G}_{0}=0.5$, and $a$ is a dimensionless curvature parameter. It should be noted that the equation is valid only for $\gamma >{\gamma }_{\mathrm{e}}$, while for $\gamma \le {\gamma }_{\mathrm{e}}$, $G={G}_{0}$.

$$\frac{G}{{G}_{0}}=1/\left[1+ {\left(\frac{\gamma -{\gamma }_{\mathrm{e}}}{{\gamma }_{r}}\right)}^{a}\right]$$

(1)

The ${\gamma }_{\mathrm{r}}$, ${\gamma }_{\mathrm{e}}$, and $a$ parameters are defined in Eqs. (2, 3, and 4), where: ${U}_{\mathrm{c}}$ is the uniformity coefficient; $p\mathrm{^{\prime}}$ is the mean effective stress; ${p}_{a}$ is the reference atmospheric pressure; $e$ is the void ratio; and ${I}_{\mathrm{d}}$ is the relative density.

$${\gamma }_{\mathrm{r}}\left(\%\right)=0.01{{U}_{\mathrm{c}}}^{-0.3}\left(\frac{p\mathrm{^{\prime}}}{{p}_{\mathrm{a}}}\right)+0.08e{I}_{\mathrm{d}}$$

(2)

$${\gamma }_{\mathrm{e}}=0.0002+0.012{\gamma }_{\mathrm{r}}$$

(3)

$$a={{U}_{\mathrm{c}}}^{-0.075}$$

(4)

Equation 1 is extremely useful as an alternative to a bespoke suite of element tests. However, if due to imitations on the data available across some or all of a site, an engineer only had access to, e.g. ${U}_{\mathrm{c}}$ and ${I}_{\mathrm{d}}$ they would have no means to recover the stiffness degradation curve using the curve fitting approach.

This study sought to enhance the value of the extant data set of soil stiffness degradation with strain from element and in situ test data and the accompanying soil classification data by leveraging capabilities of an artificial neural network (ANN) to recover stiffness degradation curves from any number and combination of available soil classification parameters from a set of eight identified parameters. The proposed method, and freeware app based on the method, provide researchers and practicing engineers with greater ability and versatility to derive a stiffness degradation curve than currently exists.

1.2 The data set

The data set that underpins the curve fitting function given in Eq. 1 was assembled by Oztoprak and Bolton [31]. The data set features a large quantity of varied data from a range of different test types, drainage conditions, and granular soil classifications. Data are sourced from resonant column tests, triaxial tests, torsional shear tests, simple shear tests, and torsional simple shear tests, digitised and collated from 61 original publications. A total of 509 laboratory or in situ stiffness degradation curves were collected with a range of soil classification parameters available for each curve. As well as the aforementioned ${G}_{0}$, $e$, ${I}_{\mathrm{d}}$, $p\mathrm{^{\prime}}$, ${p}_{\mathrm{a}}$, and ${U}_{\mathrm{c}}$, many of the degradation curves have additional parameters available, including mean grain size (${D}_{50}$) and overconsolidation ratio (OCR).

For this study, a subset of the curves were included in which all eight of the identified parameters (${D}_{50}$, $e$, ${G}_{0}$, ${I}_{\mathrm{d}}$, OCR, $p$, ${p}_{\mathrm{a}}$, and ${U}_{\mathrm{c}}$) are available, with the original data set filtered and reformulated to exclude those curves that did not meet this requirement. No curves were discarded for any other reason, such as anomalous behaviour, presence of outliers, or similar. As such, a total of 240 curves (out of 509 possibilities) were included from 23 original publications, with a total of 2861 data points on the curves. The range of data used is illustrated in Fig. 2 along with a histogram showing the distribution of strain values. The filtered and reformulated data set utilised in this study has been made publicly available [8].

Fig. 2

Filtered data set showing (a) plot of 2861 data points from individual 240 curves, and (b) histogram showing the distribution of data points in (a)

To provide context for the results of the ANN-based approach, it is necessary to first assess the eight input parameters considered in this study. Table 1 shows the statistics relating to the eight parameters. Of note are ${D}_{50}$ and ${U}_{\mathrm{c}}$, for which the mean values are much higher than the median and indicate that there are a significant number of outliers with extremely high values. This is evident by comparing the range to the median value. ${G}_{0}$ likewise has a very large range. The effects of these parameters, both to specific cases and in general, are explored in later sections.

Table 1 Comparison of parameter statistics

1.3 Application of an Artificial Neural Network (ANN) to stiffness degradation prediction

The data set analysed in this study has eight independent input parameters that potentially influence the shape of the output curve. To make the most out of the data set, a multiple parameter nonlinear regression should be derived that can leverage information from all the potential input parameters. However, developing a solution via classical methods would require significant analysis to identify not only how each input parameter affects the output, but also how each parameter interacts with the others for combined effects on the output. Although classical approaches would be troublesome for this problem, it is very well suited to machine learning, which is natively multidimensional. Although there are several machine learning-based approaches that would be suitable to address the stiffness degradation curve challenge, the study presented in this paper explores the use of an artificial neural network (ANN). An ANN was chosen over other nonlinear regression models as it can approximate any function [11, 23] whereas other models are often limited to certain function shapes. This approach is further facilitated by the availability of a large and varied data set that will allow an ANN to be trained for a range of soil behaviours. Recent work [50] demonstrates the similar use of an ANN in predicting compression index and undrained shear strength of clays.

An ANN is a “…biologically inspired computational model, which consists of processing elements (called neurons), and connections between them with coefficients (weights) bound to the connections” [38]. For the case of stiffness degradation with strain, with a large data set consisting of inputs (i.e., strain values and associated parameters) and outputs (i.e., $G/{G}_{0}$), the weights of the ANN can be trained so that the ANN approximates the function $G/{G}_{0}=f\left(\gamma , params\right)$. It has been proven that ANNs, provided there are sufficient neurons, are universal approximators that can approximate any continuous function [11, 23]. The main benefit of such an approach is that any number of input parameters can be used and no presupposition of the shape of the stiffness degradation curve is required, such as is the case in classical curve fitting approaches.

Some background on ANNs used in this study is provided in the following section, with additional details included in the appendix. Shear stiffness degradation predictions from an ANN trained on the data set are compared with results from the existing curve fitting approach (Eq. 1). The effects of hidden neuron configuration on both performance and time usage are presented. A parametric study is presented to identify the contribution of each parameter to the overall solution. Additionally, an illustrative example showing how ANN’s could be used not to recover a single curve but a region of possible responses (i.e., a potential stiffness degradation envelope) is presented. Finally, a user-friendly graphical calculation app that implements the proposed methodology is briefly described with links for free download of the app and the requisite data set provided. This study demonstrates that ANN-based methodologies have great potential to improve upon pre-existing empirical approaches, not just in terms of improved accuracy, but also in providing additional capabilities with dealing with sparse or incomplete data.

Research into the use of ANNs within geotechnical engineering has been ongoing for several decades, with detailed summaries provided by several highly cited review papers [29, 37], as well as more broadly within civil engineering [1]. The interest in ANNs has steadily increased over time, from a handful of publications per year in the early 2000s to more than 25 per year as of 2017 [29].

A wide range of engineering problems have been addressed including pile capacity [30], settlement of foundations [42], soil behaviour [32], slope stability [19] and settlement of tunnels [40]. Recent publications demonstrate the prediction of monotonic and cyclic responses of sand [20], automated classification of sand particles by image in which a wide range of machine learning classifiers were considered [27], using machine learning methods (including ANNs) to generate constitutive models without a-priori assumptions [49], and using ANNs to predict the improvements in water retention of soils with the addition of biochar [17]. The cited publication considering biochar demonstrates the generation of soil–water characteristic curves, sigmoid curves of similar form to the stiffness degradation curves considered in this study.

2 Artificial neural network methodology

ANNs are functions that convert an input to an output. Instead of programming this function in traditional ways by algorithmically solving an equation, software is written such that the function can be generated automatically through training the ANN via an existing data set.

The basic components of an ANN (in this case a feedforward multilayer perceptron model) are illustrated in Fig. 3 and include: an input layer $\varvec{x}$; an output layer $\widehat{{\varvec{y}}}$; one or more hidden layers providing the output values ${{\varvec{A}}}_{{\varvec{L}}}$; a collection of weights $W$ and biases $b$; an activation function ${\sigma }_{L}$ for each layer; and a cost $C$ which is an error metric between the predicted output $\widehat{{\varvec{y}}}$ and the observed output ${\varvec{y}}$ [26].

Fig. 3

Schematic of an Artificial Neural Network

The output of an ANN is a function of the inputs, weights, and biases. Inputs are of course known, but weights and biases are not. After selecting initial random estimates for weights and biases, the ANN must be trained. This training procedure allows for refinements of these initial guesses of weight and bias values, with the aim of reducing the gap between the ANN output values and the true output values. A summary of the key mathematical concepts behind both the calculation of the output and the training procedure is included in the appendix of this paper.

In the process of training an ANN, the available data set is typically split (randomly) into three components [6]. The largest part will be the training set that is used as input during training iterations to optimise the weights and biases. Separate to the training set is the testing set. This is used for final assessment of the ANN. These data points are not used for training and allow the ANN to be tested against data that has not yet been seen in an effort to prevent overfitting. Overfitting is when the ANN becomes too optimised to the specific training data set, following all the subtle detail and noise present, and therefore may produce some unexpected results when applied to independent data. A third set, called the validation set, is sometimes used. Here data points are not used for training but are still assessed for error throughout the training procedure. A reducing error for the training set and an increasing error for the validation set provides an indication that overfitting has taken place and the iterative training procedure should end. In this study, 70% of data was assigned to the training set with 15% assigned to each of the testing and validation sets. Existing work [21] discusses selecting the optimal distribution of data, however, for the purposes of this study “good enough” meta-parameters are sufficient. Informal experimentation demonstrated that varying the training data percentage (with the remainder split evenly between testing and validation) between 20% and 80% had insignificant impacts on neural network performance.

The training procedure seeks to find the weights and biases that result in the lowest error between output and expected values across the training data set. It is important to recognise that there is no guarantee that this is the global minimum error. It is also important to note that the training procedure is not deterministic [36]. Different combinations of initial weights and biases (which are randomly assigned at the start) will result in different final weights and biases, as will the random distribution of data between the training and testing sets. The random initial configurations can be used to reduce the risk of finding local minima by simply repeating the procedure several times and choosing the best result.

For this study, an ANN architecture consisting of twelve hidden neurons within one hidden layer was chosen and used consistently regardless of the number of input parameters used. It would be possible, and indeed ‘more’ correct, to optimise such meta-parameters for the best results; however, in this case it was decided that consistency would allow for easier comparison and demonstration of the proof of concept. An analysis of altering the number of hidden neurons is provided later in this section and shows that the 12 selected is appropriate for all the cases considered. The activation functions applied to each layer, discussed in more detail in the appendix, were tanh on the hidden layer and simple linear on the output layer. The training algorithm used was Bayesian regularisation backpropagation as implemented in the MATLAB Deep Learning Toolbox [44]. Except where otherwise stated, meta-parameters relating to this algorithm were left as the default/recommended values.

A final consideration is that ANNs are non-deterministic. This makes accurate comparisons between differing configurations difficult. All ANNs were generated and trained 25 times, with the lowest mean square error (MSE) result taken. The MSE values are calculated using the both the training and testing subsets. Other measures of error, such as mean absolute percentage error (MAPE) were considered, but ultimately not included due to the measures inability to deal with values less than one.

3 Results and discussion

3.1 Comparison of ANN-based approach with laboratory data and published curve fit

In order to assess the suitability of an ANN-based approach to derive stiffness degradation curves for geotechnical design ANNs were trained with the data set compiled by Oztoprak and Bolton [31]. ANN outputs with varying selections of input parameters were compared with the existing approximating expression and equations proposed by Oztoprak and Bolton [31]. The ANN was used to predict a stiffness value for a given strain value and a set of geotechnical parameters, with the full stiffness degradation curve being constructed by feeding the trained ANN the set of parameters along with a range of strain values. As well as the full set of 8 geotechnical input parameters plus the strain parameter, ANNs were trained using only the four geotechnical parameters plus strain used by Oztoprak and Bolton [31], as well as with zero geotechnical parameters, i.e. strain data only. This configuration is essentially a curve of best fit through the entire data set and will serve as a base against which other combinations can be compared. Note that the 0 parameter model is named as such due to the lack of consideration for any of the eight geotechnical parameters considered in this study, even in this case the ANN does have one input for strain. Additionally, configurations in which each input parameter was discounted from the full set are examined such that the significance of the contribution of each can be identified; along with the inverse, in which each parameter is added in turn to the base configuration. An analysis of the effects of changing the number of hidden nodes is also provided.

To demonstrate the performance of the methodology, a set of eight cases were selected from the 240 available to act as an illustration. Instead of choosing only favourable cases, 7 of the 8 selected were, as far as possible, chosen to be the same cases used for this purpose by Oztoprak and Bolton [31]. Where the specific data point was unavailable due to being filtered for missing parameters, another was randomly selected from the same source reference for inclusion. A final eighth case was randomly chosen to allow for an even number of subplots.

Figure 4 presents a subplot for each of the eight selected test cases. Each subplot shows the ANN output utilising all eight available input parameters, the ANN output using the four specific input parameters used by Oztoprak and Bolton [31], and the ANN output using 0 input parameters (i.e. only the strain data). For comparison, the output of the Oztoprak and Bolton [31] equation (Eq. 1) is given, as is the laboratory stiffness curve taken from the original literature source [2, 13, 16, 33, 45, 47, 48].

Fig. 4

Comparison of ANN predictions with Eq. 1 and laboratory data for 8 arbitrarily selected cases. Solid black line indicates the prediction using Eq. 1, dashed black line the ANN prediction using all 8 input parameters, solid grey line the ANN prediction using 4 input parameters, and dashed grey line the ANN prediction using just strain as input

Overall, the results of the ANN-based approach are good regardless of which combination of input parameters is used, particularly at low strains where there is plenty of available training data. At high strains, where training data are sparse, the curves recovered by the ANN are typically of lower quality than the equation-based approach (since the latter constrains the shape of the curve) for some of the arbitrarily selected examples. However, when examining the MSE across the entire data set, it becomes apparent that the ANN-based approach represents an improvement (see Table 2).

Table 2 Comparison of global performance (MSE) of all methodologies

Table 2 shows that the MSE is smaller in cases where more input parameters are used. This does not guarantee that every individual recovered curve will be closer to the laboratory values and indeed this can be seen in Fig. 4. The ANN curve for eight parameters (Fig. 4g) shows poor fit at low and high strains, indeed poorer than when 4 or even 0 parameters are used. This suggests the 8 parameter ANN result is being skewed by one or more anomalous input values. Examining the input parameters for Fig. 4g, along with Table 1, shows that there are several values that, if not anomalous, are certainly outliers. The uniformity coefficient ${U}_{c}$ is 54, over 6 times the mean of the data set, ${D}_{50}$ is 70 mm, over 13.5 times the mean, and ${G}_{0}$ is 578 MPa, over 3.5 times the mean. This specific combination of parameters is represented by a tiny fraction of the available data such that little confidence can be had in the results, particularly at high strains where this effect is compounded due to the established sparsity of high strain data points. Selecting only the 4 ‘Oztoprak and Bolton [31]’ parameters and simply not including ${D}_{50}$ and ${G}_{0}$ eliminates the problem. This illustrates how unnecessary input parameters can have an adverse effect the accuracy of an ANN, either by adding noise or overshadowing more important correlations [3]. This example also highlights the importance of the engineer reviewing and interpreting the ANN results based on their geotechnical knowledge, since the ANN has no such knowledge. Additional constraints on the curve shape and other boundary conditions could also prevent anomalous predictions such as in Fig. 4g but must be weighed against benefits of less constraints in finding the optimal curves across the whole data space.

Also of note is the curve recovered by the 0 parameter ANN in which only strain and $G/{G}_{0}$ were used to train the network. This curve is the same for all the 8 examples provided, and indeed for the 232 curves not presented. This recovered curve essentially represents a curve of best fit for the entire data set. Despite this, the 0 parameter ANN has a lower MSE than the fitting function proposed by Oztoprak and Bolton [31]. This does not, however, mean that such a curve would be more suitable for design. The shape of an unconstrained curve with undulations visible by eye will have a lower MSE than a curve constrained to follow a smooth sigmoid ‘s’ shape, yet these undulations are not representative of true behaviour and care must be taken that the recovered behaviour is critically examined rather than blindly trusting a single error value. It should also be noted that the 0 parameter ANN curve is specific for this data set and this result would not necessarily follow for other data sets. Although in this case a single wildly undulating line of best fit is able to represent the entire data set fairly well, a data set with samples covering a wider range of particle size for instance, would likely see the opposite result.

Several possible indications of poor behaviour are apparent to the trained geotechnical engineer’s eye from Fig. 4. If, for instance, $G/{G}_{0}$ at strain 0 is significantly different to 1, or the curve undulates, it will almost certainly be unrepresentative. It should be noted that such concerns would be relevant only when a practitioner is concerned with a specific curve. If a trained ANN is used to predict the degradation curve for a specific sand, the fact that an outlier gravel with a ${D}_{50}$ of 70 mm has a badly predicted curve is largely immaterial.

It should also be remembered that Fig. 4 represents 8 out of the 240 available curves and that these examples were not chosen to showcase favourable results. Demonstrated flaws within individual plots are specific to that individual case and do not impact either the other plots or the overall performance of the network.

Figure 5 shows how MSE varies with strain. This plot was produced by calculating the squared error of every output point to the corresponding laboratory data point and finding the MSE for bins of 100 points. This figure indicates the lack of data at high strains due to increased spacing between bins and shows that all ANN configurations (and the Oztoprak and Bolton [31] equation-based methodology) perform worst at around 0.1% strain. It should also be noted that taking the mean of each bin MSE produces the same values as presented in Table 2.

Fig. 5

Demonstration of how ANN performance (MSE) varies with strain

3.2 Global analysis of results

A comparison of recovered and expected $G/{G}_{0}$ values are shown in Fig. 6 for all curves from (a) the Oztoprak and Bolton [31] equation, (b) the ANN-based approach using 4 input parameters, and (c) the ANN-based approach using all 8 input parameters. It is evident that the ANN-based approaches cluster more tightly around the 1:1 line, indicating an overall better fit to the observed data for both the 4 and 8 parameter input ANNs, with MSE values (shown in Table 2) of 0.00662, 0.00229, and 0.00208 for the equation-based and ANN-based approaches, respectively.

Fig. 6

Comparison of actual and expected values for a Eq. 1, b ANN using 4 input parameters, and c ANN using 8 input parameters

Whereas the previous discussion regarding comparisons between recovered and expected stiffness curves identified cases at the edge of the data set in which the ANN-based approach appeared to perform poorly, it is clear from this more global analysis that both ANN-based approaches perform around 3 times better, on average, than the equation-based approach based on the MSE values.

Several differences are apparent. Firstly, the equation-based approach has an enforced limit for the allowable values of $G/{G}_{0}$. The Oztoprak and Bolton [31] equation (Eq. 1) was defined based on geotechnical concepts and empirical analysis that ensure outputs make physical sense, such as $G/{G}_{0}$ being fixed at 1 for strains below the elastic threshold. This is clearly visible in the provided point cloud. The trained ANNs have no knowledge of geotechnics or physics and potential users of such methodologies must ensure the output is sensible. It would be possible to design an ANN such that physics-based rules are incorporated; however, this is beyond the scope of this paper.

The second difference is the tendency for the equation-based approach to overestimate at high $G/{G}_{0}$ values. This can be seen by examining the density of the point clouds above the 1:1 line for $G/{G}_{0}>0.8$. Although 8 out of 240 data sets is not fully representative, a close examination of Fig. 4 allows for identification of this phenomena in several of the provided subplots. The ANN-based approach can take advantage of the large number of data points at relatively low strains to provide an improved fit at low strain values at the expense of fit at high strain values, where there is little available data.

It is noted that the data set used to present these comparisons was not trimmed due to anomalous data points. Trimming outliers would improve such a comparison plot for the Oztoprak and Bolton [31] equation, but not alter the performance of the remaining data points. Trimming outliers from the ANN training set would potentially improve performance of those points still in use at the expense of a narrower applicability. A network trained to predict the stiffness curves of sands would potentially better predict the stiffness curves of sands than a network trained to predict the stiffness curves of a range of granular soils, particularly if extreme outliers are eliminated in the process.

A final consideration is that the performance of any of the trained ANN models cannot be assessed with regards to data points from outside the domain of the original data set. The standard ANN techniques of splitting the data set into training, testing, and validation subsets mitigate this issue somewhat but as stated previously, soil properties that have poor coverage within the data set tend to have more anomalous results. It is likely that the ANN models would perform poorly when fed data that has significantly different soil properties to what was included in the analysed data set. Although the data set used is large and provides good coverage over a range of engineering sands, it would be beneficial to provide alternative or supplementary data points if intending to use the described methodology for different granular soils, e.g. gravels.

3.3 Influence of architecture on runtime and performance of the Artificial Neural Network-based approach

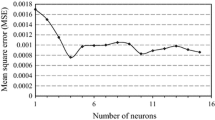
Figure 7 shows how (a) runtime and (b) performance, indicated by mean square error (MSE), vary with the number of hidden neurons used. For simplicity, only one hidden layer was considered, with hidden neuron numbers between 1 and 25 trialled. As would be expected, more hidden neurons result in a longer runtime with an approximately linear relationship. The rate of change is higher when all 8 parameters are used, as an additional hidden neuron requires 8 connections to the input neurons, whereas when only 4 inputs are used an additional hidden neuron results in only 4 extra connections to the input neurons.

Fig. 7

a Time vs hidden neurons and b Performance vs hidden neurons for 8 input parameter Neural Network and 4 (O&B) parameter ANN

Of note is that all runtime durations presented in Fig. 7 are low (a matter of seconds). Using a larger training set would increase the elapsed times. However, as per the discussion above, outside of edge cases, the data set used was of sufficient size. Despite these quick runtimes, the method is not “plug and play”. A data set cannot simply be loaded into an ANN software with a fully trained network available a few seconds later. Formal or informal experimentation into network architecture, training algorithms, and which input parameters are to be included require many runs of the training process as well as repeats to account for the non-negligible variance between runs due to the inherent randomness of the procedure.

Performance, measured by MSE, improves with an increasing number of hidden neurons with diminishing returns after around 10. Extremely high numbers of hidden neurons would cause an increase in training time and almost certainly lead to overfitting. Based on these figures, the decision to use 12 hidden neurons for the main analysis with this particular input data set is sound.

A final consideration is that performance is better for all neuron numbers with the full set of input parameters. Although some individual curves may appear to be lower quality for the reasons discussed, Fig. 7 provides further evidence that using all input parameters is, on average, better.

Table 3 presents the effects of inclusion of each input parameter, both subtractively (i.e., removing it from the full set) and additively (i.e., adding it to the empty set). The MSE for the inclusion of each parameter is presented along with the change from the MSE of the base configuration. It is reiterated that an ANN-based approach is non-deterministic and there is some inherent randomness, and although the table presents the “best” value obtained after 25 trials of each configuration, it is entirely possible that repeating this exercise would produce slightly different results. As such, this table should not be used to make fine quantitative analyses, but instead to find broad qualitative considerations that can be correlated with observations discussed earlier in this paper.

Table 3 Effects of additive and subtractive inclusion of input parameters

The first point that can be raised is that OCR has essentially zero effect when either added to the empty configuration or subtracted from the full configuration when compared to the other parameters. This is because, the overwhelming majority of tests in the database (including all 8 presented in Fig. 4) have an OCR of 1 with only a few exceptions, and as this parameter is largely uniform across the data set it makes sense that its inclusion in the training process is not particularly influential.

It was suggested in the earlier discussion that the outlier values for ${D}_{50}$, ${U}_{c}$, and ${G}_{0}$ were potentially responsible for anomalous recovered curves for some tests. Removing ${D}_{50}$ and to a lesser extent ${U}_{c}$, does appear to result in a reduction of MSE. This would fit the hypothesis that sparse data at high strain values does not allow for significant variations of some variables limiting the ANNs ability find correlations that represent the full data set, and simply omitting parameters in this case is potentially better. It should also be noted that ${D}_{50}$ is typically a poor parameter for predicting soil behaviour: a well graded, gap graded, and uniformly graded soil could all have identical ${D}_{50}$ values while having radically different particle size distributions and soil behaviours. An MSE improvement from removing $e$ is also apparent but was not something that was predicted based on earlier analysis. However, due to the inter-relationships between ${D}_{50}$, ${U}_{c}$, and $e$, this behaviour is not unexpected.

More broadly, although removal of a single parameter from the full set can, in some cases, improve and, in some cases, worsen the MSE, the effects are much smaller than the improvement gained by adding any parameter (except OCR) to the empty set. An ANN trained with the empty parameter set will output the same stiffness degradation curve for any soil properties, so it is logical that introducing even a single input parameter that has some correlation with the stiffness degradation curve would represent a meaningful improvement, as now the recovered curve will be “personalised” for each specific soil.

Although testing every possible combination of 8 parameters would not be possible due to differences in MSE often being less than random variance, it seems likely that almost any combination that has at least a few input parameters above strain alone would produce an acceptable stiffness degradation curve. Full optimisation of input parameter selection and network architecture, through a genetic algorithm-based approach [3] or similar, would be possible, but would appear to be unnecessary to recover stiffness degradation curves that would be usable in design or modelling.

The methodology used to estimate the influence of each parameter is considered appropriate for this problem due to the relatively small number of parameters considered, and the fact that the purpose was to demonstrate that any combination of the 8 considered parameters can produce a reasonable output. Although it has been demonstrated that some parameters are more influential than others, this finding is secondary. For more generalised cases, where e.g. significantly more parameters are available, or where a specific optimal combination of inputs is sought, algorithms exist to compute an ANN model sensitivity to all input parameters [35].

3.4 Discussion on variability between ANN training runs

Due to the non-determinism of the ANN training procedure, repeated runs will produce both different MSE values and different output curves. All figures and tables presented so far have been based on the “best” (i.e., lowest MSE) ANN out of 25 trials. Figure 8 shows box and whisker plots for MSE for each of the 3 ANN architectures (8 parameters, 4 parameters, and 0 parameters, as described in Sect. 3.1) generated using the results from 1000 training runs. The boxes represent the 25th and 75th percentiles and whiskers extend out to up to 3 times in interquartile range. This many runs would have been prohibitively time consuming to carry out for all the analyses in this paper and is presented here as a check to demonstrate that the results presented in Sect. 3, where each analysis was trained 25 times, are reasonable.

Fig. 8

Box and Whisker plot showing variance of ANN performance over 1000 training runs. The boxes represent the 25th and 75th percentiles and whiskers extend out to up to 3 times in interquartile range. Diamond markers represent the values used in earlier analysis as per Table 2

It is apparent that the vast majority of runs result in an MSE that is roughly comparable, with the mean being slightly higher, to those presented in Table 2 for 25 runs. Diamond markers have been plotted to represent the values used in the earlier analysis. It should be noted that there are a small number of extreme outliers that are not visible on this plot due to having MSE values an order of magnitude higher than the visible data. There are no such outliers with lower MSE values. Also apparent is the fact that the spread is lower with fewer input parameters. This is in line with previous commentary on additional parameters being a potential source of noise.

Variance between runs need not be seen as a negative. Figure 9 shows a heatmap of output curves predicted by 1000 individually trained ANNs for the example shown in Fig. 4c. To produce this heatmap, the strain-stiffness plot was split into 500 bins in each axis with 1000 output curves plotted and inclusion of each bin counted. The heatmap values represent the inclusion within each strain-stiffness bin. Although presented here only for a single example for illustrative purposes, it would be possible to use such a technique to allow for confidence intervals in the output curve rather than a single line for every case. Given the short runtimes present in Fig. 7, this technique is perfectly tractable and potentially offers a more intuitive output.

Fig. 9

Heatmap showing the range of possible output curves for example (c) from Fig. 4 predicted by 1000 individually trained ANNs

The heatmap plot also increases confidence in the validity of the ANN-based approach despite the inherent non-determinism. Even over 1000 runs, the output degradation curves are largely the same, with the exception of very high strains where the lack of available data has been identified as an issue.

3.5 Implementation of methodology into graphical calculation app

The capabilities demonstrated in this paper have been compiled into a stand-alone calculation application, programmed in MATLAB, that can be downloaded, both as source code and as an executable app [9]. The data set used in this study is bundled with the application, but as stated in Sect. 1.2 is also available as a stand-alone object [8]. It is the hope of the authors that sharing this application and the associated data set will provide a tool that is useful both for practitioners and researchers. A short video demonstrating the usage of this application has been included as supplementary material for this paper and can also be viewed at https://youtu.be/jyTPOrWE3EI.

Figure 10 shows screenshots demonstrating the main functionality of the application. Figure 10a shows the parameter input form. Users can tick the box beside every parameter that they have access to, as many or as few as that may be, and input the value in the provided box. Several example values are preloaded into the application. On pressing run, an ANN will be trained for the selected parameter set with the output curve for the input parameter values being plotted (Fig. 10b). The output curve is plotted over a point cloud of all shear stiffness degradation data in the data set to allow for qualitative judgement to be made regarding the output curve. Due to the fact that there are eight factorial combinations, it is impossible to provide pretrained ANNs. Numeric values for the output curve can be displayed and easily exported to, e.g. FEA software (Fig. 10c). Figure 10d shows a plot of actual vs expected G/G₀ values for the entire data set along with a mean squared error (MSE) value.

Fig. 10

Screenshots showing the graphical MATLAB app that implements the methodology demonstrated in this paper

4 Conclusions

This study has demonstrated that shear stiffness degradation curves can be quickly and efficiently recovered from an arbitrary number of soil classification parameters using an Artificial Neural Network (ANN)-based approach. The ANN approach exhibited lower Mean Squared Error than the existing empirical curve fitting approach using the same background data set whether all eight input parameters were used, the same specific four as used in the empirical curve fitting function, or even any individually selected parameter.

The key value of the ANN approach presented in this paper is the ability to derive a stiffness degradation curve for the soil characterisation parameters available to the engineer, rather than being constrained by requiring specific parameters, as is the case for a classical curve fitting approach (i.e., Eq. 1). In this latter case, if the specific input parameters demanded by the approximating function are not available, a curve cannot be recovered. For the ANN-based approach presented here, the engineer can always recover a stiffness degradation curve, based on any number of characterisation parameters available, providing greater ability and versatility to derive stiffness degradation curves than currently exists. Further, as shown, the mean square error of the stiffness degradation curves recovered from the ANN were always lower compared to the current curve fitting method—irrespective of the number of input parameters available.

It has been shown that the ANN-based approach is extremely resilient to factors such as network architecture and input parameter selection and, although there are methodologies to optimise such meta-parameters, initial investigation shows that such methodologies are not necessary for this case.

A user-friendly graphical calculation application has been created as part of this study that allows researchers to select and input whichever parameters they choose and/or have available from the set, and derive a stiffness degradation curve, along with uncertainty measure, for use in engineering calculations. The app, along with its source code and the required data set are available freely for download [8, 9], along with an explanatory video demonstrating its use (https://youtu.be/jyTPOrWE3EI).

Finally, this work contributes towards the evidence base of merit in machine learning techniques such as ANNs within the geotechnical context that can provide additional capabilities over more traditional empirical approaches particularly regarding sparse or incomplete site data. The key benefit is not in terms of performance or design efficiency (although there are improvements to be found in these areas) but in allowing solutions to be found where existing techniques are unable to provide them.

Appendix

This appendix contains a brief overview of the key mathematical concepts behind the Feedforward Multilayer Perceptron Artificial Neural Network (ANN) used in this study.

As per Fig. 3 in the main body of the paper, an ANN consists of an input layer $\varvec{x}$; an output layer $\widehat{{\varvec{y}}}$; one or more hidden layers each with a value ${{\varvec{A}}}_{L}$, a collection of weights $W$ and biases $b$; an activation function ${\sigma }_{L}$ for each layer. Each layer consists of one or more neurons and each neuron has a numeric value. The neuron values of the input layer are known and are described by the vector $\varvec{x}$ or alternatively ${{\varvec{A}}}_{0}$. The neuron values of hidden layer L are described by the vector ${{\varvec{A}}}_{{\varvec{L}}}$. The output layer neuron/s are represented with the vector $\widehat{{\varvec{y}}}$. Which in cases with one hidden layer could be referenced with the vector ${{\varvec{A}}}_{2}$.

Matrices of weights are used to represent the influence of each neuron of layer L−1 on neurons on layer L, where each matrix will be of size (i × j) where i is the number of neurons on layer L−1 and j is the number on layer L. Each neuron will also have a bias value, which is a single numeric value that is added and unaffected by weightings. Whereas weights are multiplicative with respect to the previous layer, biases are additive.

The values of the neurons on layer L, ${{\varvec{A}}}_{{\varvec{L}}}$, can be found with Eq. (5) with the raw values prior to activation, ${z}_{L}$, provided in Eq. (6):

$${{\varvec{A}}}_{{\varvec{L}}}={\sigma }_{L}({{\varvec{W}}}_{{\varvec{L}}}\cdot {{\varvec{A}}}_{{\varvec{L}}-1}+{{\varvec{b}}}_{{\varvec{L}}})$$

(5)

$${z}_{L}={{\varvec{W}}}_{{\varvec{L}}}{\cdot {\varvec{A}}}_{{\varvec{L}}-1}+{{\varvec{b}}}_{{\varvec{L}}}$$

(6)

The output of one layer can be used to find the value of the next layer. Equations can be chained together for an arbitrary number of layers. In cases with only one hidden layer, the output $\widehat{{\varvec{y}}}$ can be described as a function of the input and two layers of weights, biases, and activation functions as shown in Eq. 7:

$$\widehat{{\varvec{y}}}= {\sigma }_{2}({{\varvec{W}}}_{2}\cdot {\sigma }_{1}({{\varvec{W}}}_{1}\cdot {\varvec{X}}+{{\varvec{b}}}_{1})+{{\varvec{b}}}_{2})$$

(7)

Activation functions are used to limit the value of a neuron to within a certain range, e.g. $0\le {{\varvec{A}}}_{{\varvec{L}}}\le 1$ by passing the neuron value through the logistic function, or $-1\le {{\varvec{A}}}_{{\varvec{L}}}\le 1$, using the tanh function. Applying activation functions allows for mimicry of biological neurons and enables nonlinear relationships to be found. An ANN without nonlinear activation functions would essentially function as a linear regression solver [39]. Activation functions on the output neuron/s are determined by the problem type. An ANN designed to, e.g. categorise images, could have an output neuron for each category that is assigned a value between 0 and 1, which represents the likelihood of each category being correct. In cases where this is not necessary or desirable such as finding an unknown relationship in which outputs can be greater than 1, a simple linear activation function can be used for the output layer. It will be necessary to know the derivative of the activation function. It should be noted that there are many activation functions that could potentially have been used, including some more recent developments than the chosen tanh, such as ReLu. Qualitative investigation showed that tanh typically produced the most realistic output curve with other possibilities having very little impact in terms of measured error, which matches findings in literature [41]. For the activation function used in this project, tanh, the derivative is as shown in Eq. (8).

$${\mathrm{where}} \, \sigma ({z}_{L} )={\mathrm{tanh}}({z}_{L} ),\, \sigma ^{\prime} ({z}_{L} )=1-{\sigma ({z}_{L} )}^{2}$$

(8)

The cost $C$ allows for assessment of the performance of an ANN. The goal is to train the network such that the output values $\widehat{{\varvec{y}}}$ are as close as possible to the expected values ${\varvec{y}}$. The cost is calculated using the Mean Square Error (MSE). Cost is used during the training process along with the training data sets and after completion to assess performance with the testing data set. Equation (9) shows how cost is calculated [46].

$$C={\sum ({\varvec{y}}-\widehat{{\varvec{y}}})}^{2}$$

(9)

Moving forwards through the ANN is called feed forward. It is likely that the initial guesses for weighting and bias will result in a large error and as such must be adjusted to improve the performance of the ANN. A process called back propagation [34] is used to determine how the weights and biases are to be adjusted to minimise the cost.

The minimisation problem can be thought of as a multidimensional plot with a dimension for each weight, bias and input. Such a plot would be impossible to visualise. A 3D representation could be made in which peaks and troughs would allow for visual identification of local minima. Finding the gradient (in each dimension) at the current location allows for movement towards the nearest local minima through a process called gradient descent [10]. The gradient of cost with regard to ${{\varvec{W}}}_{2}$ can be written using the chain rule as shown in Eq. (10) [18].

$$\frac{\partial C}{\partial {W}_{2}}=\frac{\partial C}{\partial {A}_{2}}\frac{\partial {A}_{2}}{\partial {z}_{2}}\frac{\partial {z}_{2}}{\partial {W}_{2}}$$

(10)

The terms in Eq. (10) are defined as follows. The derivative of cost function with respect to output is shown in Eq. (11). The derivative of output with respect to z (sum prior to activation function) is the derivative of the activation function and is shown in Eq. (12). The derivative of z with respect to weight is simply weight, Eq. (13).

$$\frac{\partial C}{\partial {A}_{2}}=2({\varvec{y}}-\widehat{{\varvec{y}}})$$

(11)

$$\frac{\partial {A}_{2}}{\partial {z}_{2}}= {\sigma }^{\mathrm{^{\prime}}}\left({z}_{2}\right)=\sigma \mathrm{^{\prime}}({{\varvec{W}}}_{2}\cdot {{\varvec{A}}}_{1}+{{\varvec{b}}}_{2})$$

(12)

$$\frac{\partial {z}_{2}}{\partial {W}_{2}}= {{\varvec{W}}}_{2}$$

(13)

Having calculated the above components, the differential of cost with respect to weight can be found with Eq. (14). Additionally, the differential of cost with respect to both bias and neuron value at L−1 can similarly be found. These terms are provided in Eqs. (15 and 16).

$$\frac{\partial C}{\partial {W}_{2}}=2\left({\varvec{y}}-\widehat{{\varvec{y}}}\right)\cdot {\sigma }^{\mathrm{^{\prime}}}\left({{\varvec{W}}}_{2}\cdot {{\varvec{A}}}_{1}+{{\varvec{b}}}_{2}\right)\cdot {{\varvec{A}}}_{1}$$

(14)

$$\frac{\partial C}{\partial {{\varvec{b}}}_{2}}=2\left({\varvec{y}}-\widehat{{\varvec{y}}}\right)\cdot {\sigma }^{\mathrm{^{\prime}}}\left({{\varvec{W}}}_{2}\cdot {{\varvec{A}}}_{1}+{{\varvec{b}}}_{2}\right)\cdot \boldsymbol{ }1$$

(15)

$$\frac{\partial C}{\partial {A}_{1}}=2\left({\varvec{y}}-\widehat{{\varvec{y}}}\right)\cdot {\sigma }^{\mathrm{^{\prime}}}\left({{\varvec{W}}}_{2}\cdot {{\varvec{A}}}_{1}+{{\varvec{b}}}_{2}\right)$$

(16)

As ${{\varvec{A}}}_{1}$ is a function of ${{\varvec{W}}}_{1}\cdot {\varvec{X}}+{{\varvec{b}}}_{1}$ the chain can be continued further to find the gradients relating to ${{\varvec{W}}}_{1}$ etc. When the gradients have been found, they can simply be added to the weight and bias matrices and the process repeated. After many iterations, values should be found that give a reasonable error compared to expected outputs.