Skip to main content
SpringerLink
Log in

Limit analysis of 2-D and 3-D structures based on an ellipsoid yield criterion

  • Research Paper
  • Published:
Acta Geotechnica Aims and scope Submit manuscript

Abstract

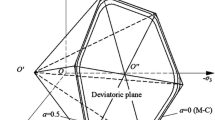
In this paper, a nonlinear numerical technique is developed to calculate the limit load and failure mode of structures obeying an ellipsoid yield criterion by means of the kinematic limit theorem, nonlinear programming theory and displacement-based finite element method. Using an associated flow rule, a general yield criterion expressed by an ellipsoid equation can be directly introduced into the kinematic theorem of limit analysis. The yield surface is not linearized and instead a nonlinear purely kinematic formulation is obtained. The nonlinear formulation has a smaller number of constraints and requires less computational effort than a linear formulation. By applying the finite element method, the kinematic limit analysis with an ellipsoid yield criterion is formulated as a nonlinear mathematical programming problem subject to only a small number of equality constraints. The objective function corresponds to the dissipation power which is to be minimized and an upper bound to the plastic limit load of a structure can then be calculated by solving the minimum optimization problem. An effective, direct iterative algorithm has been developed to solve the resulting nonlinear programming formulation. The calculation is based purely on kinematically admissible velocities. The stress field does not need to be calculated and the failure mode of structures can be obtained. The proposed method can be used to calculate the bearing capacity of clay soils in a direct way. Some examples are given to illustrate the validity and effectiveness of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

References

  1. ABAQUS theory manual (version 6.3). HKS inc., USA, 2002

  2. Capsoni A, Corradi L, Vena P (2001) Limit analysis of orthotropic structures based on Hill’s yield condition. Int J Solids Struct 38:3945–3963

    Article  Google Scholar 

  3. Chen HF, Liu YH, Cen ZZ, Xu BY (1998) Numerical analysis of limit load and reference stress of defective pipelines under multi-loading systems. Int J Pressure Vessels Piping 75:105–114

    Article  Google Scholar 

  4. Collins IF, Boulbibane K (2000) Geotechnical analysis of unbound pavements based on shakedown theory. J Geotech Geoenvir Eng 126:50–59

    Article  Google Scholar 

  5. Drucker DC, Prager W, Greenberg HJ (1952) Extended limit analysis design theorems for continuous media. Q Appl Math 9:318–389

    Google Scholar 

  6. Francescato P, Pastor J (1997) Lower and upper numerical bounds to the off-axis strength of unidirectional fiber-reinforced composite by limit analysis methods. Eur J Mech A Solids 16:213–234

    Google Scholar 

  7. Gotsis PK, Chamis CC, Minnetyan L (2002) Application of progressive fracture analysis for predicting failure envelopes and stress-strain behaviors of composite laminates: a comparison with experimental results. Comp Sci Tech 62:1545–1559

    Article  Google Scholar 

  8. Hill R (1948) A theory of the yielding and plastic flow of anisotropic metals. Proc R Soc Lond 193:282–287

    Google Scholar 

  9. Hill R (1951) On the state of stress in a plastic-rigid body at the yield point. Phil Mag 42:868–875

    Google Scholar 

  10. Himmelblau DM (1972) Applied nonlinear programming. McGraw-Hill Book Company, New York

    Google Scholar 

  11. Huh H, Yang WH (1991) A general algorithm for limit solutions of plane stress problems. Int J Solids Struct 28:727–738

    Article  Google Scholar 

  12. Li HX, Liu YH, Feng XQ, Cen ZZ (2001) Micro/macromechanical plastic limit analyses of composite materials and structures. Acta Mechanica Solida Sinica 14:323–333

    Article  Google Scholar 

  13. Li HX, Liu YH, Feng XQ, Cen ZZ (2003) Limit analysis of ductile composites based on homogenization theory. Proc R Soc Lond A 459:659–675

    Google Scholar 

  14. Liu YH, Cen ZZ, Xu BY (1995) A numerical method for plastic limit analysis of 3-D structures. Int J Solids Struct 32:1645–1658

    Article  Google Scholar 

  15. Lyamin AV, Sloan SW (2002) Upper bound limit analysis using linear finite elements and non-linear programming. Int J Numer Anal Meth Geomech 26:181–216

    Article  Google Scholar 

  16. Lyamin AV, Sloan SW (2002) Lower bound limit analysis using non-linear programming. Int J Numer Meth Engng 55:573–611

    Article  Google Scholar 

  17. Lysmer J (1970) Limit analysis of plane problems in soil mechanics. J Soil Mech Found Div, ASCE 96:1311–1334

    Google Scholar 

  18. Mackenzie D, Boyle JT (1993) A method of estimating limit loads by iterative elastic analysis, I – Simple examples. Int J Pressure Vessels Piping 53:77–96

    Article  Google Scholar 

  19. Mackenzie D, Boyle JT, Hamilton R (2000) The elastic compensation method of limit and shakedown analysis: a review. Proc IMechE J Strain Anal Eng Des 35:171–188

    Article  Google Scholar 

  20. Maier G (1969) Shakedown theory in perfect elastoplasticity with associated and nonassociated flow-laws: a finite element linear programming approach. Meccanica 4:250–260

    Article  Google Scholar 

  21. Maier G, Carvelli G, Cocchetti G (2000) On direct methods of shakedown and limit analysis. Plenary Lecture, 4th Euromech Solid Mechanics Conference, Metz

  22. Ponter ARS, Carter KF (1997) Limit state solutions based upon linear elastic solutions with a spatially varying elastic modulus. Comp Meth Appl Mech Engng 140:237–258

    Article  Google Scholar 

  23. Ponter ARS, Fuschi P, Engelhardt M (2000) Limit analysis for a general class of yield conditions. Eur J Mech A Solids 19:401–421

    Article  Google Scholar 

  24. Ponter ARS, Chen HF, Boulbibane M, Habibullah M (2002) The linear matching method for the evaluation of limit loads, shakedown limits and related problems. In: Fifth World congress on computational mechanics, Austria

  25. Shapiro JF (1979) Mathematical programming: structures and algorithms. A Wiley-Interscience Publication, New York

    Google Scholar 

  26. Sloan SW (1988) Lower bound limit analysis using finite elements and linear programming. Int J Numer Anal Methods Geomech 12:2671–2685

    Article  Google Scholar 

  27. Sloan SW, Kleeman PW (1995) Upper bound limit analysis using discontinuous velocity fields. Comput Methods Appl Mech Eng 127:293–314

    Article  Google Scholar 

  28. Sloan SW, Randolph MF (1982) Numerical prediction of collapse loads using finite element methods. Int J Numer Anal Meth Eng Geomech 6:47–76

    Article  Google Scholar 

  29. Turgeman S, Pastor J (1982) Limit analysis: a linear formulation of the kinematic approach for axisymmetric mechanic problems. Int J Num Anal Meth Geomech 6:109–128

    Article  Google Scholar 

  30. Yu HS, Netherton MD (2000) Performance of displacement finite elements for modeling incompressible materials. Int J Numer Anal Meth Eng Geomech 24:627–653

    Article  Google Scholar 

  31. Yu HS, Sloan SW (1994) Limit analysis of anisotropic soils using finite elements and linear programming. Mech Res Commun 6:545–554

    Article  Google Scholar 

  32. Yu HS, Sloan SW (1997) Finite element limit analysis of reinforced soils. Comput Struct 3:567–577

    Article  Google Scholar 

  33. Yu HS, Houlsby GT, Burd HJ (1993) A novel isoparametric finite element formulation for axisymmetric analysis of nearly incompressible materials. Int J Num Meth Eng 36:2453–2472

    Article  Google Scholar 

  34. Yu HS, Sloan SW, Kleeman PW (1994) A quadratic element for upper bound limit analysis. Eng Comput 11:195–212

    Google Scholar 

  35. Zhang YG, Lu MW (1995) An algorithm for plastic limit analysis. Comp Meth Appl Mech Engrg 126:333–341

    Article  Google Scholar 

  36. Zhang PX, Lu MW, Hwang K (1991) A mathematical programming algorithm for limit analysis. Acta Mechanica Sinica 7:267–274

    Article  Google Scholar 

  37. Zienkiewicz OC, Taylor RL, Too TM (1971) Reduced integration technique in general analysis of plates and shells. Int J Num Meth Eng 3:275–290

    Article  Google Scholar 

  38. Zouain N, Herskovits J, Borges LA, Feijüo RA (1993) An iterative algorithm for limit analysis with nonlinear yield functions. Int J Solids Struct 30:1397–1417

    Article  Google Scholar 

Download references

Acknowledgment

The work reported in this paper is supported by a grant from the UK’s Engineering and Physical Sciences Research Council (EPSRC) and the authors are grateful for this support.

Author information

Authors and Affiliations

  1. Department of Engineering Science, University of Oxford, Parks Road, Oxford, OX1 3PJ, UK

    H. X. Li

  2. School of Civil Engineering, The University of Nottingham, University Park, Nottingham, NG7 2RD, UK

    H. S. Yu

Authors
  1. H. X. Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. H. S. Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to H. X. Li.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Li, H.X., Yu, H.S. Limit analysis of 2-D and 3-D structures based on an ellipsoid yield criterion. Acta Geotech. 1, 179–193 (2006). https://doi.org/10.1007/s11440-006-0020-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11440-006-0020-x

Keywords

Search

Navigation