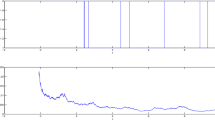
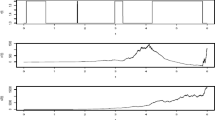
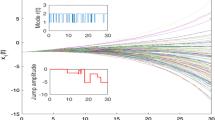
Abstract
Although the mean square stabilization of hybrid systems by feedback control based on discretetime observations of state and mode has been studied by several authors since 2013, the corresponding almost sure stabilization problem has received little attention. Recently, Mao was the first to study the almost sure stabilization of a given unstable system ẋ(t) = f(x(t)) by a linear discrete-time stochastic feedback control Ax([t/τ]τ)dB/(t) (namely the stochastically controlled system has the form dx(t) = f(x(t))dt + Ax([t/τ]τ)dB/(t), where B(t) is a scalar Brownian, τ > 0, and [t/τ] is the integer part of t/τ. In this paper, we consider a much more general problem. That is, we study the almost sure stabilization of a given unstable hybrid system ẋ(t) = f(x(t), r(t)) by nonlinear discrete-time stochastic feedback control u(x([t/τ]τ)dB(t) (so the stochastically controlled system is a hybrid stochastic system of the form dx(t) = f(x(t), r(t))dt + u(x([t/τ]τ))dB(t), where B(t) is a multi-dimensional Brownian motion and r(t) is a Markov chain.
Article PDF
Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.Avoid common mistakes on your manuscript.
References
Black F, Scholes M. The pricing of options and corporate liabilities. J Political Economy, 1973, 81: 637–654
Berman A, Plemmons R J. Nonnegative Matrices in the Mathematical Sciences. Philadelphia: Society for Industrial and Applied Mathematics, 1994
Krishnamurthy V, Wang X, Yin G. Spreading code optimization and adaptation in CDMA via discrete stochastic approximation. IEEE Trans Inform Theor, 2004, 50: 1927–1949
Luo Q, Gong Y Y, Jia C X. Stability of gene regulatory networks with Lévy noise. Sci China Inf Sci, 2017, 60: 072204
Luo Q, Shi L L, Zhang Y T. Stochastic stabilization of genetic regulatory networks. Neurocomputing, 2017, 266: 123–127
Mao W H, Deng F Q, Wan A H. Robust H 2/H ∞ global linearization filter design for nonlinear stochastic time-varying delay systems. Sci China Inf Sci, 2016, 59: 032204
Mao X R. Stability of Stochastic Differential Equations With Respect to Semimartingales. London: Longman Scientific and Technical, 1991
Mao X R. Exponential Stability of Stochastic Differential Equations. New York: Marcel Dekker, 1994
Tang M, Meng Q. Stochastic evolution equations of jump type with random coefficients: existence, uniqueness and optimal control. Sci China Inf Sci, 2017, 60: 118202
Willsky A S, Levy B C. Stochastic stability research for complex power systems. DOE Contract LIDS MIT Report No. ET-76-C-01-2295, 1979
Sworder D D, Rogers R O. An LQ-solution to a control problem associated with a solar thermal central receiver. IEEE Trans Automat Contr, 1983, 28: 971–978
Yin G, Liu R H, Zhang Q. Recursive algorithms for stock liquidation: a stochastic optimization approach. SIAM J Optim, 2002, 13: 240–263
Zhang Q. Stock trading: an optimal selling rule. SIAM J Control Optim, 2001, 40: 64–87
Anderson W J. Continuous-Time Markov Chains. New York: Springer, 1991
Ji Y, Chizeck H J, Feng X, et al. Stability and control of discrete-time jump linear systems. Contr Theor Adv Tech, 1991, 7: 247–270
Mariton M. Jump Linear Systems in Automatic Control. New York: Marcel Dekker, 1990
Skorohod A V. Asymptotic Methods in the Theory of Stochastic Differential Equations. Providence: American Mathematical Society, 1989
Yin G, Zhang Q. Continuous-Time Markov Chains and Applications: a Singular Perturbation Approach. New York: Springer-Verlag, 1998
Shaikhet L. Stability of stochastic hereditary systems with Markov switching. Theory Stoch Proc, 1996, 2: 180–183
Mao X R. Stability of stochastic differential equations with Markovian switching. Stochastic Processes Their Appl, 1999, 79: 45–67
Arnold L, Crauel H, Wihstutz V. Stabilization of linear systems by noise. SIAM J Control Optim, 1983, 21: 451–461
Basak G K, Bisi A, Ghosh M K. Stability of a random diffusion with linear drift. J Math Anal Appl, 1996, 202: 604–622
Khasminskii R Z. Stochastic Stability of Differential Equations. Leiden: Sijthoff and Noordhoff, 1981
Mao X R. Stochastic stabilization and destabilization. Syst Control Lett, 1994, 23: 279–290
Mao X R. Stochastic Differential Equations and Their Applications. 2nd ed. Chichester: Horwood Publishing Limited, 2007
Appleby J A D, Mao X R. Stochastic stabilisation of functional differential equations. Syst Control Lett, 2005, 54: 1069–1081
Mao X R, Yuan C G. Stochastic Differential Equations With Markovian Switching. London: Imperial College Press, 2006
Mao X R, Yin G G, Yuan C G. Stabilization and destabilization of hybrid systems of stochastic differential equations. Automatica, 2007, 43: 264–273
Scheutzow M K R. Stabilization and destabilization by noise in the plane. Stochastic Anal Appl, 1993, 11: 97–113
Mao X R. Stabilization of continuous-time hybrid stochastic differential equations by discrete-time feedback control. Automatica, 2013, 49: 3677–3681
Mao X R, Liu W, Hu L J, et al. Stabilization of hybrid stochastic differential equations by feedback control based on discrete-time state observations. Syst Control Lett, 2014, 73: 88–95
You S, LiuW, Lu J, et al. Stabilization of hybrid systems by feedback control based on discrete-time state observations. SIAM J Control Optim, 2015, 53: 905–925
Song G, Zheng B C, Luo Q, et al. Stabilisation of hybrid stochastic differential equations by feedback control based on discrete-time observations of state and mode. IET Control Theor Appl, 2017, 11: 301–307
Mao X R. Almost sure exponential stabilization by discrete-time stochastic feedback control. IEEE Trans Automat Contr, 2016, 61: 1619–1624
Acknowledgements
The authors would like to thank Leverhulme Trust (Grant No. RF-2015-385), Royal Society (Grant No. WM160014, Royal Society Wolfson Research Merit Award), Royal Society and Newton Fund (Grant No. NA160317, Royal Society–Newton Advanced Fellowship), Engineering and Physics Sciences Research Council (Grant No. EP/K503174/1), National Natural Science Foundation of China (Grant Nos. 61503190, 61473334, 61403207), Natural Science Foundation of Jiangsu Province (Grant Nos. BK20150927, BK20131000), and Ministry of Education (MOE) of China (Grant No. MS2014DHDX020) for their financial support. The first author would like to thank Chinese Scholarship Council for awarding him the scholarship to visit the University of Strathclyde for one year.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Song, G., Lu, Z., Zheng, BC. et al. Almost sure stabilization of hybrid systems by feedback control based on discrete-time observations of mode and state. Sci. China Inf. Sci. 61, 70213 (2018). https://doi.org/10.1007/s11432-017-9297-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11432-017-9297-1