A Lightweight Chaos-Based Medical Image Encryption Scheme Using Random Shuffling and XOR Operations

Abstract

Medical images possess significant importance in diagnostics when it comes to healthcare systems. These images contain confidential and sensitive information such as patients’ X-rays, ultrasounds, computed tomography scans, brain images, and magnetic resonance imaging. However, the low security of communication channels and the loopholes in storage systems of hospitals or medical centres put these images at risk of being accessed by unauthorized users who illegally exploit them for non-diagnostic purposes. In addition to improving the security of communication channels and storage systems, image encryption is a popular strategy adopted to ensure the safety of medical images against unauthorized access. In this work, we propose a lightweight cryptosystem based on Henon chaotic map, Brownian motion, and Chen’s chaotic system to encrypt medical images with elevated security. The efficiency of the proposed system is proved in terms of histogram analysis, adjacent pixels correlation analysis, contrast analysis, homogeneity analysis, energy analysis, NIST analysis, mean square error, information entropy, number of pixels changing rate, unified average changing intensity, peak to signal noise ratio and time complexity. The experimental results show that the proposed cryptosystem is a lightweight approach that can achieve the desired security level for encrypting confidential image-based patients’ information.

1 Introduction

The telemedicine is a fast growing field of providing medical care for patients remotely where the patient and the healthcare provider are not physically present at the same location. The patient’s confidential information such as medical images are shared through communication channels of Internet or cellular network. Such a modern healthcare system demands efficient framework capable of storing medical images such that they are always accessible only to authorized users present at any geological position. The cloud storage systems can provide such a platform, however, these systems are vulnerable to cyber attacks particularly when designed below security standards. Nevertheless, the researchers have largely focused on designing computer-based strategies for improving patient care. However, the techniques to achieve the desired level of security of the confidential information in both of the storage systems and the communication channels has lagged somewhat. In this situation, one way of protecting the medical images is through encryption schemes where the images are encrypted in such a way that they become useless for the users with no encryption information in hand. Some of the security solution for telemedicine applications are discussed in [13, 32].

The digital images communication in medicine (DICOM) is recognized as an international standard (ISO 12052) for medical imaging in modern electronic healthcare system. There are various DICOM tools and systems designed for diagnostic purposes in pre-procedural medical analysis. Such systems are highly dependent on signal processing to visualize internal organs of the human body. Moreover, today’s medical operations are mostly controlled by artificial intelligence (AI) enabled systems with integrated sensors. These real-time decision making systems, that sometimes even collaborate in sensitive surgical operations, produce as well as depend on sensitive medical data which is generally in the form of digital images. Usually, to protect these medical images that contain sensitive information about patients requires a robust system with real-time safeguarding techniques. In fact, the e-health systems, just like ordinary cloud storage systems, are vulnerable to various types of attacks, therefore, storing the medical images in its original form are comparatively easy to access by breaching system’s security protocols only. Moreover, the management and transmission of medical data between different cloud systems adapted by different hospitals or medical centers increases this vulnerability. As a result, an efficient, robust, and computationally agile system is needed to safeguard sensitive medical images against attacks irrespective of the storage systems and the communication protocols [8].

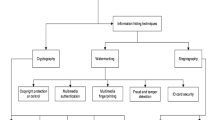
The data security systems can be divided into two types: hiding information and encrypting information. The hiding information is further classified into steganography and watermarking. The steganography tries to cover or mask the data such that the existence of data is concealed during sharing. On the other hand, in cryptography, the encripted sensitive data is visible publicly, however, the values are obscure to the viewers. Furthermore, watermarking relies on embedding a unique identification watermark to the raw data. Here, the watermarked signature is extracted at the receiving end. The aim is to prevent illegal exploitation of copyrighted or confidential contents. Besides, the concept of information encryption is to convert the plain data (original contents) into some indecipherable form before transmission. The objective is to preserve the contents in a way that it can be recovered by authorized users through decryption. The image encryption is achieved in such a way, i.e, by distorting each pixel of the image [19, 21, 22, 34].

Chaos-based cryptography is an innovative domain that employs various chaotic maps to generate random sequencing for digital medical image encryption [1, 6, 28, 36, 42, 43, 46]. These simple chaotic maps exhibit unique properties including non-linearity (NL), sensitivity towards initial conditions, strange attractors with different initial keys, and randomness. These properties can be used in order to design a robust cryptosystem [27, 29, 30, 33, 40, 41].

The initial conditions of the system are very important as they are the secret keys that should be known only to authorized persons. Without having information about these keys, the data can not be decrypted by anyone. In fact, initial conditions of the system are sensitive particularly because hackers and unauthorized users usually apply a minute change to try and decrypt the secured content. The high sensitive system means that changing small values will display profoundly strange attractors and as a result, hackers will be incapable of decrypting the original content. In addition, the strength of any cryptosystem is assessed by its computational complexity, while the transmission rate determines the efficiency of the whole system.

Claude Shannon originally introduced the copulated properties of confusion (substitution) and diffusion (permutation) in 1949 [38]. When coupled, these properties assisted in generating random numbers. Later, random numbers were applied to encrypt digital images. These copulated properties of confusion and diffusion can permute (swap) the pixel position of an image or substitute (change the pixels’ values), either way, providing high-level security. Early researchers and cryptographers in the field utilized one or the other to design cryptosystems, however, cryptosystems with partial strengths were not sufficient to provide adequate security. Therefore, cryptographers started incorporating different features of confusion and diffusion that resulted in improved security [9, 26]. The subsequent phase of diffusion is based on pixel distortion, i.e., adding an additional layer of protection to the initial phase of confusion and thus improving overall security.

In general, two principal components are necessary to design a secure scheme; the image encryption symmetric key and the private/public key. In a symmetric key-based cryptosystem the authorized user uses the same key at both ends. This type of security is widely adopted for computer security. The single key is shared between two or more users i.e., use to convert plain text to ciphertext and cipher text to plain text back. In Fig. 1, the symmetric key is applied to the chaos-based cryptographic algorithm that assisted to change the plain image into the encrypted image. In the next stage, the same key is applied to the encrypted image resulting in decryption process. In subsequent Fig. 2 the plain data is converted to ciphered data using encryption key K1. By applying key K1 the data is transformed into ciphered form. Furthermore the ciphered data is decrypted in the second phase using same key K1 resulting in getting back plain data at the other end. Systematic charts of two different symmetric key-based encryption and decryption methods are shown in Figs. 1 and 2.

Fig. 1

Schematic chart for symmetric key based encryption and decryption

Fig. 2

Another view of symmetric key based encryption and decryption process

2 Literature Review

A secure cryptography scheme can be achieved through different ways, including permutation and substitution, as shown in Fig. 3. Over the last decade, researchers have proposed a number of image encryption schemes using chaos theory [1, 2, 9]. Nevertheless, hybrid cryptosystems are emerging as more promising solution due to their efficiency in encrypting multimedia information [10, 14]. Existing hybrid systems use different domains and multiple substitution or permutation processes to shuffle and distort the pixels of an image. For instance, chaotic maps are famous for producing dynamic and unpredictable responses in return. Given the sheer variation in initial condition, these chaotic maps produce drastic output and highly random sequencing that are difficult to decrypt without having specific knowledge of the system. Therefore, these maps are widely used for image encryption to achieve secure communication [39].

Most of the researchers and cryptographers adapted such approaches to design cryptosystems with significant computational security. For instance, [31] proposed a cryptosystem based on the external key having two chaotic maps to generate random numbers. The external key emerges from the algorithm’s initial state and is altered infrequently in order to encrypt each block cipher that comprises a total of sixteen pixels. It is very difficult for attackers to discover the secret key that has been used in the proposed method. Similarly, [11] designed a hybrid scheme of a chaotic map and a coupled map lattice. A single dimension chaos map is used, however, the combined effect is an improved key space ultimately improving protection across the entire system profoundly sensitive to its initial condition. In another study, [15] proposed a system by adapting a hyperchaotic map to depreciate prediction times. This cryptosystem includes permutation of pixels via shuffling matrix along with diffusion of the shuffled pixels. This system provides improved security due to the high key space associated with it.

Fig. 3

Pixel’s permutation and substitution with round process

3 Contributions

The major contribuions of this work are summarized as follows:

• Designing an effective multi-stage cryptographic algorithm for medical images encryption using substitution-permutation technique. This multi-stage cryptographic algorithm uses random numbers generated from chaos maps which reduces correlation among the pixels of the digital medical images.

• Designing a contemporary variant of the chaos-based confusion-diffusion approach that is capable of achieving a significant higher entropy and NIST-based randomness results as compared to existing methods. The results demonstrate that the proposed encryption algorithm is able to generate highly secured medical encrypted images.

• Analysing the performance of the proposed system and comparing it with several existing approaches used in cryptosystems. The efficiency of each algorithm is analyzed in terms of histogram consistency analysis and its variance (HCAV), adjacent pixels correlation analysis (APCA), contrast analysis (CA), homogeneity analysis (HA), energy analysis (EA), NIST analysis, information entropy (IE), a number of pixels changing rate (NPCR), unified average changing intensity (UACI), mean square error (MSE), peak to signal noise ratio (PSNR), and time complexity (TC).

4 Proposed Algorithm

This section presents detailed discussion about the proposed algorithm that uses multiple chaotic maps.

4.1 Henon Chaotic Map (HCM)

The Henon chaotic map (HCM), sometimes termed a Henon–Pomeau attractor map [17], is a dynamic system of the discrete domain and one of the most reviewed examples of two-dimensional dynamic structures that exhibit unpredictable/chaotic behaviours. The Henon map functions by taking any point along the plane ($x_{n}$, $y_{n}$) and mapping it to a new one, a process that can be formulated as follows:

$$\begin{aligned} \left\{ \begin{array}{l} x_{n+1}=1-a x_{n}^{2}+y_{n} \\ y_{n+1}=b x_{n} \end{array}\right. \end{aligned}$$

(1)

As demonstrated above, this type of chaotic map relies on parameters a and b. Moreover, this system is established for the value set to $a = 1.4$ and $b = 0.3$. A Henon map is chaotic in terms of traditional values, but may prove to be either chaotic, intermittent, or else converging to aperiodic orbit for other values of the same parameters. An overview of the Henon map’s behaviour and form at the different values for its parameters can be obtained from its orbit diagram. The two-dimensional chaotic map is plotted for 10,000 iterations with the initial conditions set to $a = 1.4$ and $b = 0.3$ as shown in Fig. 4.

Fig. 4

Two-dimensional chaotic map for 1000 iterations with initial conditions $a = 1.4$ and $b = 0.3$

4.1.1 Brownian Motion (BM)

Brownian motion is a spontaneous movement of particles floating in a liquid or gas substance due to interactions between the fast-moving atoms and molecules. The particles’ evolution along three primary directions (here, X, Y, and Z) and mathematically defined as [23]:

$$\begin{aligned} X=r \sin a \cos b, \quad Y=r \sin a \sin b, \quad Z=r \cos a \end{aligned}$$

(2)

whereas $0 \le r \le +\infty , 0 \le b \le 2 \pi , \text{ and } 0 \le a \le \pi$

The state of the Brownian particle can be measured when sufficient information is related to the direction of motion of the particles, i.e., particles’ movement along three directions (X, Y, and Z). The specific time duration ($t_{p}$) is the time needed for the particles to move erratically, the total number of particles ($n_{p}$) involved in the zig-zag motion, and the number of impulses per change in track associated with a zig-zag motion. The step length is signified as $r = 2$ and the pseudo-random function is utilized to determine the direction of movement of particles. In this way, the X, Y, and Z attributes of each Brownian particle’s position can be obtained. BM can be generated using the Monte Carlo process. In three-dimensional model, we estimate the Brownian motion of 10 particles, using a vector of $10\times 3$ to store Brownian particles’ impulse per change in track, particle positions, and distance. The plot diagram for all the three directions is shown in Fig. 5. The proposed scheme uses zig-zag random numbers for all the three directions generated for number of particles (np) = 256, total estimated time (t) = 60 s, and number of impulses per change in track = N = $100\times t$ (where: t = 60 s).

Fig. 5

Brownian motion particles along X (a), Y (b), and Z (c) directions for $np = 10$, $t = 10$ s, and N/T =10

4.1.2 Chaotic Chen System (CSS)

The chaotic system based on [12] is defined as follows:

$$\begin{aligned} \begin{array}{l} \frac{\mathrm {d} x}{\mathrm {d} t}=a(y-x) \\ \frac{\mathrm {d} y}{\mathrm {d} t}=(c-a) x-x z+c y \\ \frac{\mathrm {d} z}{\mathrm {d} t}=x y-b z \end{array} \end{aligned}$$

(3)

Here a, b, and c $\in$ $R^{3}$ are fixed. If $a = 35$, $b =3$, and $c =35$. then the system involves a chaotic attractor, as can be seen in Fig. 6.

The fractional order of this particular system may be defined as:

$$\begin{aligned} \begin{array}{l} \frac{\mathrm {d}^{q} x}{\mathrm {d} t^{9}}=a(y-x) \\ \frac{\mathrm {d}^{q} y}{\mathrm {d} t^{q}}=(c-a) x-x z+c y \\ \frac{\mathrm {d}^{q} z}{\mathrm {d} t^{q}}=x y-b z \end{array} \end{aligned}$$

(4)

where q reflects a fractional order with a specific range of $0 < q \le 1$. Therefore, we change only the derivative order q and the system parameter c in this simulation process while the rest of the input variables remain constant. Notice that both q and c varied as shown in [24]. Simulations are conducted for a step size of 0.1 with q = 0.6–0.1. Here, the simulation results indicate that, with an order beyond 3, chaos tends to exist. While q = 0.6–0.1 is in the time step 0.1, there are also chaotic attractors, as the process shown in Fig. 6 demonstrates. However, if the value of $q = 0$, then no chaotic behaviour is perceived, implying that q = 0–0.1 is the lowest fractional-order q limit at which it is possible for chaos to exist in this kind of system (4). 0.3 was the lowest order at which we discerned chaos.

Fig. 6

3D view of CCM attractor within a fractional-order Chen system (4) with $q = 0.1$ while (a, b, c) = (35, 3, 28)

Fig. 7

Flow chart for the proposed medical cryptosystem

4.2 The Proposed Algorithm

The flow chart of the proposed medical image encryption scheme is shown in Fig. 7. From the flow chart, one can see that, several essential steps are required in order to develop a cryptosystem secure enough to encrypt medical images given as follows:

• (1) Let I be the plain text image with $m \times n$ representing the entire dimension of a grey medical image:, m and n represent the image’s rows and columns, respectively. Each medical image I is resized to a dimension of $512\times 512$ pixels and is stored as $I_{2}$.

• (2) The resized image $I_{2}$, which now contains 262144 pixels, is further divided into an equal number of blocks, i.e., $I_{2}$ = $B_{1}$, $B_{2}$, $B_{3}$, $B_{4}$ ... $B_{4096}$, in which the total number of blocks is 4096 and each block size is $8\times 8$. An example of this step is shown in Fig. 8.

• (3) In third step, a two-dimensional HCM is initiated and utilized to shuffle the $8\times 8$ pixels of each generated block, thus producing an intra-block shuffling process. An example of this step is shown in Fig. 9.

• (4) After the intra-block shuffling process, image blocks are shuffled up to third phase as shown in Fig. 10.

• (5) Next, a three-dimensional BM is initiated to define the number of particles concerning the time in seconds, the defining position of various particles, and the number of impulses per each change made in each of three directions (X, Y, and Z): e.g., X = $T_{1}$, Y = $T_{2}$, and Z = $T_{3}$. These particles are then stored in each direction, where the total number of particles (np) = 256, the total time (t) = 60, and the number of impulses per change in track = N = $100.*t$ (where: t = 60 s).

• (6) In this step, BM is iterated N = 1536256 times for each direction $T_{1}$, $T_{2}$, and $T_{3}$, respectively. The first 1274112 values are discarded, i.e., 1536256–1274112 = 262144 from each direction, as a means of overcoming the transient effect. Some of the random values thus generated are then stored in $U_{1}$, $U_{2}$, and $U_{3}$, respectively.

• (7) The values of $U_{1}$, $U_{2}$, and $U_{3}$ are now multiplied by $10^{14}$ to get $V_{1}$, $V_{2}$, and $V_{3}$, respectively. Moreover $V_{1}$, $V_{2}$, and $V_{3}$ are now reshaped to a matrix of $512\times 512$ pixels, which helps achieve random sequencing for three directions: $W_{1}$, $W_{2}$, and $W_{3}$.

• (8) Absolute and round function are applied to $W_{1}$, $W_{2}$, and $W_{3}$ and the new values are stored in $X_{1}$, $X_{2}$, and $X_{3}$, respectively.

• (9) Modulus 256 operation is applied to $X_{1}$, $X_{2}$, and $X_{3}$ in order to get $Y_{1}$, $Y_{2}$, and $Y_{3}$.

• (10) Zig-zag random sequencing $Y_{1}$, $Y_{2}$, and $Y_{3}$ is multiplied with the permuted grey image of third phase $I_{3}$ (step 4) and the new values are stored in $Z_{1}$, $Z_{2}$, and $Z_{3}$.

• (11) Fractional-order CCS is added for an additional layer of security increasing the randomness and entropy of the proposed scheme.

• (12) Finally, the most recent output of the CCS random sequencing is bitwise XOR with $Z_{1}$, $Z_{2}$, and $Z_{3}$ to get new encrypted layers such as $Z1_{encrypt}$, $Z2_{encrypt}$, $Z3_{encrypt}$.

Fig. 8

Initial phase of pixels distribution into No. of blocks = 4096

Fig. 9

Second phase of pixels shuffling inside each block

Fig. 10

Third phase of itself blocks shuffling

5 Experimental Results

The performance of the proposed scheme is evaluated using a number of tests which are widely used to assess the statistical measures and security of cryptosystems. The tests for performance analysis of proposed scheme are conducted on a core i5 CPU with 4GB RAM.

5.1 Histogram Analysis

All numerical values repeated in an image can be visually observed with the help of a histogram. The histogram of an image should have a uniform distribution and must not have sharp peaks. The uniform distribution of an encrypted image on a histogram shows the higher security and efficiency of the encryption.

The proposed scheme is tested on various grey medical images, including Chest, Brain, and MR and the results are displayed in Figs. 11, 12, 13, 14, 15, 16, 17, 18, 19 and 20. The pixels are permuted (shuffled) during the first phase of the proposed scheme, achieving the outputs shown in Figs. 11, 12 and 13. Each medical image is encrypted along with three directions, as shown in Figs. 14, 15 and 16. Histograms of each medical image in these three directions are shown in Figs. 17, 18, 19 and 20. In Fig. 17 pixels are not uniformly distributed while in Figs. 18, 19 and 20, each pixel of encrypted image is uniformly distributed along three different directions. Thus the results of this test have validated our suggested cryptosystem (Fig. 21). Furthemore, three dimensional (3D) view of plaintext and encrypted histogram is also shown in Figs. 22, 23, 24 and 25. One can also confirm from Figs. 22, 23, 24 and 25 that the histogram of encrypted image is flat as compared to plaintext image.

Fig. 11

Chest X-ray Original image, shuffling of block values, shuffling of blocks themselves

Fig. 12

Brain image Original image, shuffling of block values, shuffling of blocks themselves

Fig. 13

MR image Original image, shuffling of block values, shuffling of blocks themselves

Fig. 14

Chest X-ray Encrypted image along X encrypted image along Y, encrypted image along Z

Fig. 15

Brain image Encrypted image along X, encrypted image along Y, encrypted image along Z

Fig. 16

MR image Encrypted image along X , encrypted image along Y, encrypted image along Z

Fig. 17

Plain image histograms Chest X-ray histogram, Brain image histogram, MR image histogram

Fig. 18

Encrypted chest X-ray image histograms encrypted along X, encrypted along Y, encrypted along Z

Fig. 19

Encrypted brain image histograms encrypted along X, encrypted along Y, encrypted along Z

Fig. 20

Encrypted MR image histograms encrypted along X, encrypted along Y, encrypted along Z

Fig. 21

3D view plain image histograms Chest X-ray histogram, Brain image histogram, MR image histogram

Fig. 22

3D view chest image histograms Chest X-ray histogram along X horizontally, Chest X-ray histogram along X diagonally, Chest X-ray histogram along X vertically

Fig. 23

3D view chest image histograms Chest X-ray histogram along Y horizontally, Chest X-ray histogram along Y diagonally, Chest X-ray histogram along Y vertically

Fig. 24

3D view chest image histograms Chest X-ray histogram along Z horizontally, Chest X-ray histogram along Z diagonally, Chest X-ray histogram along Z vertically

5.2 Adjacent Pixels Correlation Analysis

An important parameter to demonstrate the diffusion and confusion properties of a ciphertext image is correlation among adjacent pixels. In this work, a total of four thousand random pairs of pixels adjacent horizontally, diagonally, and vertically from both the plaintext and the ciphertext versions of the same image were analyzed. Mathematically, correlation can be calculated as:

$$\begin{aligned} r_{x y}&= \frac{E((x-E(x))(y-E(y)))}{\sqrt{D(x) D(y)}} \end{aligned}$$

(5)

$$\begin{aligned} E(x)&= \frac{1}{N} \sum _{i=1}^{N} x_{i} \end{aligned}$$

(6)

$$\begin{aligned} D(x)&= \frac{1}{N} \sum _{i=1}^{N}\left( x_{i}-E(x)\right) ^{2}. \end{aligned}$$

(7)

where x and y represent the grey-scale values of adjacent pixels and E(x) is the expected mean value. The range of correlation coefficient is between -1 to 1, where 1 illustrate the exact similarity between two images or pixels. It is essential to obtain a value near 0 for the case of maximum uncorrelated pixels, i.e., highly random values. The pixel similarity or dissimilarity between plaintext and ciphertext for different medical images is explored and compared with [5, 18, 25, 35]. The results of our proposed system are given in Table 1. The visual results given in Fig. 25 reflect all the three directions of the grey scale chest X-ray image where pixels are joined diagonally. These results demonstrate that for the plaintext, image pixels remain highly similar. The pixels are diffused in all directions when the pixels of encrypted images have zero resemblance to one other as shown in Figs. 26, 27, and 28. In Table 1 the dimension wise plain image mean values of Chest, Brain, and MR for each direction X, Y and Z are approximately 0.9982, 0.9703, and 0.9838, respectively that is near to 1 which corresponds to high correlation between pixels of an image for each direction. The mean values are calculated in case of encrypted image of Chest, Brain, and MR for each direction. The calculated encrypted average or mean values are 0.0015, $-0.0034$, and 0.0019. The values lies in between 0 and $-1$ for encrypted image. These results validate our proposed cryptosystem.

Table 1 Correlation coefficient values for each dimension

Fig. 25

Plaintext chest image pixels correlation Chest X-ray pixel’s correlation along X, Chest X-ray pixel’s correlation along Y, Chest X-ray pixel’s correlation along Z

Fig. 26

Encrypted chest image pixels correlation Chest X-ray pixels correlation along X horizontally, Chest X-ray pixels correlation along X diagonally, Chest X-ray pixels correlation along X vertically

Fig. 27

Encrypted chest image pixels correlation Chest X-ray pixels correlation along Y horizontally, Chest X-ray pixels correlation along Y diagonally, Chest X-ray pixels correlation along Y vertically

Fig. 28

Encrypted chest image pixels correlation Chest X-ray pixels correlation along Z horizontally, Chest X-ray pixels correlation along Z diagonally, Chest X-ray pixels correlation along Z vertically

5.3 Homogeneity, Energy and Contrast Analyses

The proximity of grey-level co-occurrence matrices (GLCM) elements in this system can be quantified by homogeneity analysis. Statistical combinations of pixel luminosity or grey levels is illustrated by GLCM tables. Here, if the homogeneity values are lower, the encryption scheme is considered efficient. Mathematically, this can be calculated as:

$$\begin{aligned} H=\sum _{x, y=1}^{M} \frac{g(x, y)}{1+|x-y|}. \end{aligned}$$

(8)

where g(x, y) stands for the grey-level co-occurrence matrices in GLCM.

Contrast is the disparity in luminosity or colours by which the items in a picture can be differentiated and viewers can recognise various objects. The difference in the intensity of adjacent pixels across the entire image can be computed with contrast analysis. For increased security, the contrast values should be higher, which demonstrates the amount of randomness in the ciphertext image. The mathematical expression for contrast is:

$$\begin{aligned} \text{ Contrast }=\sum _{i, j=1}^{M}|x-y|^{2} p(x, y). \end{aligned}$$

(9)

where p(x, y) signifies the grey-level co-occurrence matrices in GLCM.

Energy is another parameter that can be calculated from the GLCM. In this case, the energy analysis measures squared elements. The mathematical expression for energy calculation is as follows:

$$\begin{aligned} \text{ Energy } =p({\varvec{x}}, {\varvec{y}})^{2}. \end{aligned}$$

(10)

where p(x, y) signifies the overall number of grey-level co-occurrence matrices.

Homogeneity values for the test images of the Chest, Brain, and MR images are depicted in Tables 2, 3 and 4. The obtained average value of homogeneity for the proposed scheme is 0.3906 for x, y, and z direction of each medical image. Moreover, the output of proposed scheme is compared with the schemes proposed by [4, 20], and the results are illustrated in Table 5. The values generated by the proposed scheme are comparatively flat compared to the results in Table 5. Therefore, the low values obtained demonstrate the efficiency of our proposed cryptosystem.

Energy values of ciphertext images for chest X-ray, brain, and MR medical images are also shown in Tables 3 and 4. The calculated average value for the suggested scheme is 0.0156. Moreover, the outputs/results achieved with our proposed cryptosystem are compared to those obtained with [4, 20], as presented in Table 5. The proposed scheme values are comparatively low to those calculated in Table 5, and hence, the examined results have authenticated our proposed cryptographic scheme. Moreover, from Tables 2, 3 and 4, the values of contrast can be also observed for ciphertext images in each of the three directions. The calculated average value is higher relative to existing schemes, such as [4, 20], as presented in Table 5. The proposed scheme values are comparatively high to those calculated in . Therefore it is evident that the proposed scheme possesses better resistance to attacks than many present schemes.

Table 2 Average homogeneity, energy, and contrast analysis along X direction

Table 3 Average homogeneity, energy, and contrast analysis along Y direction

Table 4 Average homogeneity, energy, and contrast analysis along Z direction

Table 5 Existing results of homogeneity, energy, and contrast analysis

5.4 NIST Analyses

The National Institute of Standards and Technology (NIST), a US organization, issued specific guidelines that should be followed to secure data. Fifteen tests are proposed by the NIST as a means of estimating an encryption algorithm’s randomness and measuring its strength. The performance of our proposed scheme is benchmarked in Table 6, which reveals that the proposed system has passed all fifteen tests recommended by the NIST and hence suggests that it is secure enough for digital encryption of medical images.

Table 6 Building type, scope, scale, privacy issues, sampling time and accuracies of various occupancy techniques

5.5 Differential Attack Analysis

Immunity to differential attacks is also a vital feature of an encryption algorithm. Two tests that can determine resistance to differential assaults are: (1) Number of pixels changing rate and (2) Unified average changing intensity. Each of the aforementioned tests is discussed in detail below, where both were run upon two encrypted images whose corresponding plaintext images differ from each other by a single pixel.

5.5.1 Number of Pixels Changing Rate

The number of changing pixels in two cipher text images can be calculated via the NPCR test when there is a minute difference of one pixel between their plaintext images. The mathematical formula of NPCR is:

$$\begin{aligned} N P C R=\frac{\sum _{i, j} D(i, j)}{M \times N} \times 100 \% \end{aligned}$$

(11)

If the two ciphertext images has same value then $D(i, j)=0$ while in the opposite case, $D(i, j)=1$. The upper limit of the NCPR is 100%, but for a a good cryptosystem, the NCPR value should be higher than 99.5%.

5.5.2 Unified Average Changing Intensity

The degree of averaged changed intensity between two cipher text images can be calculated with the help of UACI test when there is a one-pixel difference between their corresponding plaintext images. The mathematical expression for UACI is:

$$\begin{aligned} U A C I=\frac{1}{M \times N}\left[ \sum _{i, j} \frac{\left| C_{1}(i, j)-C_{2}(i, j)\right| }{255}\right] \times 100 \% \end{aligned}$$

(12)

$C_{1}(i, j)$ and $C_{2}(i, j)$ signify the encrypted images whose corresponding plaintext images are different from each other by a single pixel. The values of NCPR and UACI can be observed from Table 7. The proposed scheme values are compared to that of [37], as shown in Table 8. The values imply that our proposed cryptographic scheme offers much higher security relative to both modern and traditional cryptosystems.

Table 7 NPCR and UACI calculated value for chest, brain, and MR image along three direction

Table 8 Comparison of NPCR and UACI values

5.6 Pixel’s Inconsistency Analysis

5.6.1 Mean Square Error

Mean Square Error (MSE) is the measurement of the average of the squares of errors between two images and can be used to analyze Avalanche effect. According to this security metric, a substantial change in the encrypted image should result when a small change is introduced in either the plaintext image or the key. The mathematical expression for MSE is as follows:

$$\begin{aligned} \mathrm {MSE}=\frac{1}{W \times H} \sum _{i=1}^{W} \sum _{j=1}^{n}(\mathrm {X}(i, j)-\mathrm {Y}(i, j))^{2}, \end{aligned}$$

(13)

where W and H illustrates the image’s dimensions, while X and Y represents the couple of encrypted images themselves whose corresponding encryption keys are only different from each other by a single bit. The measured value of MSE should be high for any robust cryptosystems. We applied the MSE test on all three medical images for three different directions. The average MSE value (in all directions) for chest image, brain, and MR image is 11017, 12320, and 11468 respectively, as shown in Table 9. The proposed scheme assessed values are also compared to the present scheme of [44], demonstrated in Table 10. The higher value obtained by our proposed scheme showed that it is extremely secure, even in comparison to the most modern cryptosystems.

5.6.2 Peak to Signal Noise Ratio

This ratio gauges the change in pixel value between a plaintext image and its encrypted counterpart. For the calculation of PSNR, the plaintext image is chosen as a signal and the encrypted image as noise. Mathematically, PSNR is calculated as:

$$\begin{aligned} {\text {PSNR}}=10 \times \log _{10}\left( \frac{255 \times 255}{\mathrm {MSE}}\right) \end{aligned}$$

(14)

where MSE is the mean squared error value. Lower value PSNR indicates that there is a significant difference between the original plaintext image and its encrypted counterpart, which is desirable for an encryption algorithm. Here we applied the PSNR test on all three medical images for three different directions. The average PSNR value (in all directions) for chest X-ray, brain, and MR medical images were 7.74, 7.26, and 7.57 respectively, as shown in Table 9. These results are even better than the values obtained by [44], as shown in Table 10. The lower values we achieved intimate that our designed cryptosystem outperforms existing cryptosystems significantly.

Table 9 Calculated MSE and PSNR values

Table 10 Comparison of average MSE and PSNR values

5.7 Entropy Analysis

The most critical parameter for the measurement of unpredictability and randomness is entropy as first introduced by Claude E. Shannon in 1948 [16]. According to Shannon, information entropy describes the degree of uncertainty present in any communication system. The mathematical formula for the calculation of information entropy is:

$$\begin{aligned} H(m)=\sum _{i=0}^{2^{N}-1} p\left( m_{i}\right) \log \frac{1}{p\left( m_{i}.\right) } \end{aligned}$$

(15)

where $p(m_i)$ represents the probability of $m_i$. and N shows the number of bits representing $m_i$. If we consider a random source that can generate $2^K$ symbols, the entropy value will be K. As we know that a gray-scale image has $2^8$ grey levels, so the entropy value should ideally be eight, but practically it is a value less than eight. The calculated results are benchmarked for chest, brain, and MR in Tables 11, 12 and 13 respectively. The results are compared to those achieved by [45] Sun’s scheme, [45] Baptisa’s scheme, [45] Wong’s scheme , and [45] Xiang’s scheme as shown in Table 14. The calculated entropy values generated by our proposed cryptosystem are higher than those obtained from existing schemes.

Table 11 Information entropy test for chest image along three direction

Table 12 Information entropy test for MR image along three direction

Table 13 Information entropy test for brain image along three direction

Table 14 The comparison of entropy values

5.7.1 Time Complexity

An efficient cryptosystem should take up minimum resources and time during its execution process. To analyze the time and computational complexity needed here, our proposed algorithm is compared with those offered by [3, 3, 7, 7, 23, 23]. The host system used for this timing complexity analysis had the following specifications: Acer TMP-455-MG computer with intel core i5 CPU and 8GB RAM. The computer was also equipped with AMD Radeon graphics card (HD 8750M) and the Matlab 2013(a) simulation tool was used to perform the experiments. The time complexity results in Table 15 demonstrate the higher agility of the proposed scheme with 1.53 s of time required to encrypt a medical image, which is much lower than the time required by existing techniques.

Table 15 Time complexity of the proposed scheme and its comparison

6 Conclusion

In this paper, we highlighted the need for a secure encryption technique to protect confidential information in medical images. An enhanced image encryption scheme is proposed that combines chaos theory with Brownian motion (BM) and Chen’s chaotic system (CCS) to achieve the desired level of security in storage systems of hospitals and medical centers. The proposed system achieves confusion through two-dimensional Henon chaotic map (HCM), whereas diffusion is obtained using BM and CCS. Furthermore, the reliability and security of the proposed system are analyzed and compared with existing techniques using the following parameters. The NIST and entropy measures are obtained through randomness test, the consistency and variance through histogram examination, and the pixel similarity using a coefficient of correlation. Other performance analysis parameters include energy, contrast, homogeneity, mean square error, peak to signal noise ratio, number of pixels changing the rate, unified average changing intensity, and computational complexity. The results show that the proposed system outperform existing image encryption systems in terms of higher security. In addition, the proposed system requires less computational resources and, at the same time, offer fast processing making it suitable for application in real-time encryption. As a future direction, the proposed encryption scheme can be modified in order to encrypt other media formats including audio and video.