Performance of Spectrum Sharing System in Gamma Shadowed Nakagami-m Fading Environment

Abstract

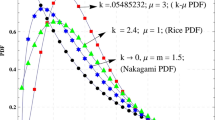
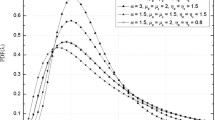
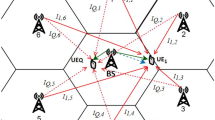
In this paper, the performance of spectrum sharing system in composite Nakagami-m/gamma shadowed channels is analyzed. The environments (of primary and secondary users) corrupted only by noise or interference are considered in details. The novel analytical expressions for outage probability, moment generation function and ergodic capacity are derived in a form of fast-computable Meijer’s G functions, for both mentioned scenarios. Numerical results illustrate the impact of fading and shadowing phenomena on system performance, and appropriate comparison between noise- and interference-limited cases is presented.

Appendix

The PDF of the RV z defined as $z = x_{1} /x_{2}$ can be evaluated using the method given in [18] as

$$p_{z} \left( z \right) = \int\limits_{0}^{\infty } {x_{2} p_{{x_{1} }} \left( {zx_{2} } \right)p_{{x_{2} }} \left( {x_{2} } \right)dx_{2} } .$$

(18)

Considering the PDFs given in a form of (4) and representing K _{k − m} (.) by Meijer’s G function as $K_{\nu } \left( x \right) = \frac{1}{2}G_{0,2}^{2,0} \left( {\frac{{x^{2} }}{4}\left| \begin{aligned} & \_\hfill \\ & \frac{\nu }{2}, - \frac{\nu }{2} \hfill \\ \end{aligned} \right.} \right)$, [17, Eq. (8.4.23.1)], (18) becomes

$$\begin{aligned} p_{z} \left( z \right) & = \left( {\frac{{m_{1} k_{1} }}{{\varOmega_{1} }}} \right)^{{\frac{{m_{1} + k_{1} }}{2}}} \left( {\frac{{m_{2} k_{2} }}{{\varOmega_{2} }}} \right)^{{\frac{{m_{2} + k_{2} }}{2}}} \frac{{z^{{\frac{{m_{1} + k_{1} }}{2} - 1}} }}{{\varGamma \left( {m_{1} } \right)\varGamma \left( {k_{1} } \right)\varGamma \left( {m_{2} } \right)\varGamma \left( {k_{2} } \right)}} \\ & \quad \times \int\limits_{0}^{\infty } {x_{2}^{{\frac{{m_{1} + k_{1} + m_{2} + k_{2} }}{2} - 1}} } G_{0,2}^{2,0} \left( {\frac{{zx_{2} m_{1} k_{1} }}{{\varOmega_{1} }}\left| \begin{aligned} & - \\ & \frac{{k_{1} - m_{1} }}{2}, - \frac{{k_{1} - m_{1} }}{2} \\ \end{aligned} \right.} \right)G_{0,2}^{2,0} \left( {\frac{{x_{2} m_{2} k_{2} }}{{\varOmega_{2} }}\left| \begin{aligned} & - \\ & \frac{{k_{2} - m_{2} }}{2}, - \frac{{k_{2} - m_{2} }}{2} \\ \end{aligned} \right.} \right)dx_{2} . \\ \end{aligned}$$

(19)

Integral in (19) can be solved in the exact closed-form, using the procedure of integrating product of two Meijer’s G functions [17, Eq. (2.24.1.1)], in a way

$$\begin{aligned} p_{z} \left( z \right) & = z^{{\frac{{m_{1} + k_{1} }}{2} - 1}} \left( {\frac{{m_{1} k_{1} \varOmega_{2} }}{{m_{2} k_{2} \varOmega_{1} }}} \right)^{{\frac{{m_{1} + k_{1} }}{2}}} \frac{1}{{\varGamma \left( {m_{1} } \right)\varGamma \left( {k_{1} } \right)\varGamma \left( {m_{2} } \right)\varGamma \left( {k_{2} } \right)}} \\ & \quad \times G_{2,2}^{2,2} \left( {\frac{{m_{1} k_{1} \varOmega_{2} z}}{{m_{2} k_{2} \varOmega_{1} }}\left| \begin{aligned} & 1 - \frac{{m_{1} + k_{1} + 2k_{2} }}{2},1 - \frac{{m_{1} + k_{1} + 2m_{2} }}{2} \\ & \frac{{k_{1} - m_{1} }}{2}, - \frac{{k_{1} - m_{1} }}{2} \\ \end{aligned} \right.} \right). \\ \end{aligned}$$

(20)

Furthermore, to obtain the PDF of RV $\gamma^{NL} = c_{1} z$ we use the transformation $p_{\gamma }^{NL} \left( \gamma \right) = \frac{{p_{z} \left( z \right)}}{{\frac{d\gamma }{{dz}}}}\left| \begin{aligned} \hfill \\ z = \frac{\gamma }{{c_{1} }} \hfill \\ \end{aligned} \right.$ [18], and the PDF of equivalent SNR is derived in the form of (6).

Considering the same procedure as for deriving the PDF p _z (z), the PDF of the RV y = z/x ₃, can be also obtained. Substituting (20) into $p_{y} \left( y \right) = \int\limits_{0}^{\infty } {x_{3} p_{z} \left( {yx_{3} } \right)p_{{x_{3} }} \left( {x_{3} } \right)dx_{3} }$, with the help of [17, Eqs. (8.4.23.1), (2.24.1.1)] we get

$$\begin{aligned} p_{y}^{IL} \left( y \right) & = \frac{1}{{\varGamma \left( {m_{1} } \right)\varGamma \left( {k_{1} } \right)\varGamma \left( {m_{2} } \right)\varGamma \left( {k_{2} } \right)\varGamma \left( {m_{3} } \right)\varGamma \left( {k_{3} } \right)}}y^{{\frac{{m_{1} + k_{1} }}{2} - 1}} \\ & \quad \times G_{4,2}^{2,4} \left( {\frac{{m_{1} k_{1} \varOmega_{2} \varOmega_{3} y}}{{m_{2} k_{2} m_{3} k_{3} \varOmega_{1} }}\left| \begin{aligned} & 1 - \frac{{m_{1} + k_{1} + 2k_{2} }}{2},1 - \frac{{m_{1} + k_{1} + 2m_{2} }}{2},\chi_{2} \\ & \frac{{k_{1} - m_{1} }}{2}, - \frac{{k_{1} - m_{1} }}{2} \\ \end{aligned} \right.} \right). \\ \end{aligned}$$

(21)

Finally, the PDF of the RV $\gamma^{IL} = c_{2} y$ is found, relating to transformation $p_{\gamma }^{IL} \left( \gamma \right) = \frac{{p_{y} \left( y \right)}}{{\frac{d\gamma }{{dy}}}}\left| \begin{aligned} \hfill \\ y = \frac{\gamma }{{c_{2} }} \hfill \\ \end{aligned} \right.$ [18], in a form given in (8).