Skip to main content

Advertisement

Springer Nature Link
Log in

Optimal Design for Shock Damper with Genetic Algorithm to Control Water Hammer Effects in Complex Water Distribution Systems

  • Published:
Water Resources Management Aims and scope Submit manuscript

Abstract

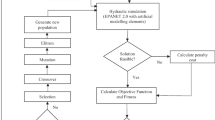
In this paper, the optimal design of a shock damper and its parameters along with the layout for controlling water hammer effects in water distribution systems (WDS) will be investigated. The shock damper and its governing equations are introduced, and then complex network (networks with loop and branching) analysis is performed during the occurrence of a water hammer. Because of the multiple design parameters for the shock damper and the complexity of WDS transient analysis, a standard optimization problem is defined with maximum safety as the objective function. The problem constraints are the network analysis equations in the event of a water hammer. Also, other constraints consist of the maximum and minimum range of the allowable head and values of the design parameters for the shock damper. To solve the problem, a genetic algorithm is used, and a flow chart of the problem-solving design with the genetic algorithm is also provided. To investigate the efficiency and the effect of the optimal design of the shock damper, two real water distribution networks are considered, which include a gravity network and a pumping network. To create a water hammer occurrence in the first network, the amount of discharge in one of the nodes is suddenly increased, while in the second network, one of the control valves is closed suddenly. These events lead to the occurrence of a significant water hammer in each system, resulting in both positive and negative waves and water column separation phenomena. The results show the high effectiveness of the optimal shock damper design in controlling the effects of transient flows in real water distribution systems, thereby increasing those systems’ effectiveness.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  • Afshar M, Rohani M (2008) Water hammer simulation by implicit method of characteristic. Int J Press Vessel Pip 85(12):851–859

    Article  Google Scholar 

  • Afshar MH, Rohani M (2009) Optimal operation of pipeline systems using Genetic Algorithm. IEEE Congress on Evolutionary Computation, Trondheim, pp 1399–1405

    Google Scholar 

  • Barna IF, Imre AR, Baranyai G, Ézsöl G (2010) Experimental and theoretical study of steam condensation induced water hammer phenomena. Nucl Eng Des 240(1):146–150

    Article  Google Scholar 

  • Bostan M, Afshar M, Khadem M, Akhtari A (2016) A hybrid MILP-LP-LP approach for the optimal design and operation of unconfined groundwater utilization systems. J Water Supply Res Technol AQUA 65(3):208–219

    Article  Google Scholar 

  • Bostan M, Afshar MH, Khadem M (2015) Extension of the hybrid linear programming method to optimize simultaneously the design and operation of groundwater utilization systems. Eng Optim 47(4):550–560

    Article  Google Scholar 

  • Bostan M, Akhtari AA, Bonakdari H (2018a) Deriving the governing equation for a shock damper to model the unsteady flow caused by sudden valve closure and sudden demand change. J Water Supply Res Technol AQUA 67(2):202–210

    Article  Google Scholar 

  • Bostan M, Akhtari AA, Bonakdari H, Gharabaghi B, Noori O (2018b) Investigation of a new shock damper system efficiency in reducing water hammer excess pressure due to the sudden closure of a control valve. ISH Journal of Hydraulic Engineering:1–9. https://doi.org/10.1080/09715010.2018.1479665

  • Chaudhry MH (1979) Applied hydraulic transients. Springer, New York

    Google Scholar 

  • Djebedjian B, Mohamed MS, Mondy AG, Rayan MA (2005) Network optimization for steady flow and water hammer using genetic algorithms. Ninth International Water Technology Conference, IWTC 2005, Sharm El-Sheikh, pp 1101–1115

    Google Scholar 

  • Jung BS, Karney B (2004) Fluid transients and pipeline optimization using GA and PSO: The diameter connection. Urban Water J 1(2):167–176

    Article  Google Scholar 

  • Jung BS, Karney BW (2003) Optimum selection of hydraulic devices for water hammer control in the pipeline systems using genetic algorithm. 4th ASME-JSME Joint Fluids Engineering Conference, Hawaii, pp 2877–2883

    Google Scholar 

  • Jung BS, Karney BW (2006) Hydraulic optimization of transient protection devices using GA and PSO approaches. J Water Resour Plan Manag 132(1):44–52

    Article  Google Scholar 

  • Kim S-H (2010) Design of surge tank for water supply systems using the impulse response method with the GA algorithm. J Mech Sci Technol 24(2):629–636

    Article  Google Scholar 

  • Larock BE, Jeppson RW, Watters GZ (1999) Hydraulics of pipeline systems. CRC Press, Boca Raton

    Book  Google Scholar 

  • Polanco G, Virk MS, Mughal UN, Victor S, Da Paixao José VA, Orlando A (2015) Encapsulated Water Hammer: Theoretical/Experimental Study. World Journal of Engineering and Technology 3(03):290

    Article  Google Scholar 

  • Popescu M, Arsenie D, Vlase P (2003) Applied Hydraulic Transients: For Hydropower Plants and Pumping Stations. CRC Press, Boca Raton

    Google Scholar 

  • Rao SS, Rao SS (2009) Engineering optimization: theory and practice. John Wiley & Sons, New York

    Book  Google Scholar 

  • Rohani M, Afshar MH (2010) Simulation of transient flow caused by pump failure: Point-Implicit Method of Characteristics. Ann Nucl Energy 37(12):1742–1750

    Article  Google Scholar 

  • Sattar AM (2016) A probabilistic projection of the transient flow equations with random system parameters and internal boundary conditions. J Hydraul Res 54(3):342–359

    Article  Google Scholar 

  • Sattar AM, El-Beltagy M (2016) Stochastic solution to the water hammer equations using polynomial chaos expansion with random boundary and initial conditions. J Hydraul Eng 143(2):04016078

    Article  Google Scholar 

  • Skulovich O, Bent R, Judi D, Perelman LS, Ostfeld A (2015) Piece-wise mixed integer programming for optimal sizing of surge control devices in water distribution systems. Water Resour Res 51(6):4391–4408

    Article  Google Scholar 

  • Skulovich O, Perelman LS, Ostfeld A (2016) Optimal closure of system actuators for transient control: an analytical approach. J Hydroinf 18(3):393–408

    Article  Google Scholar 

  • Stephenson D (2004) Closure to “Simple Guide for Design of Air Vessels for Water Hammer Protection of Pumping Lines” by D. Stephenson. J Hydraul Eng 130(3):275–275

    Article  Google Scholar 

  • Tian W, Su G, Wang G, Qiu S, Xiao Z (2008) Numerical simulation and optimization on valve-induced water hammer characteristics for parallel pump feedwater system. Ann Nucl Energy 35(12):2280–2287

    Article  Google Scholar 

  • Tijsseling A, Vardy A, Fan D (1996) Fluid-structure interaction and cavitation in a single-elbow pipe system. Journal of Fluids and Structures 10(4):395–420

    Article  Google Scholar 

  • Wylie EB (1984) Fundamental equations of waterhammer. J Hydraul Eng 110(4):539–542

    Article  Google Scholar 

  • Wylie EB, Streeter VL, Suo L (1993) Fluid transients in systems. Prentice Hall, Englewood Cliffs

    Google Scholar 

  • Zhang HX, Kou ZM, Wu J, Lu CY (2011) Numerical Simulation and Analysis of Hydraulic Excitation System Based on Water Hammer by the Method of Characteristics. Adv Mater Res 295-297:2210–2215

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering, College of Engineering, Kermanshah Branch, Islamic Azad University, Kermanshah, Iran

    Mohammad Bostan

  2. Department of Civil Engineering, College of Engineering, Razi University, Kermanshah, Iran

    Ali Akbar Akhtari & Hossein Bonakdari

  3. Department of Civil Engineering, Isfahan University of Technology, Isfahan, Iran

    Farshad Jalili

Authors
  1. Mohammad Bostan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ali Akbar Akhtari
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Hossein Bonakdari
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Farshad Jalili
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hossein Bonakdari.

Ethics declarations

Conflict of Interest

None.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bostan, M., Akhtari, A.A., Bonakdari, H. et al. Optimal Design for Shock Damper with Genetic Algorithm to Control Water Hammer Effects in Complex Water Distribution Systems. Water Resour Manage 33, 1665–1681 (2019). https://doi.org/10.1007/s11269-019-2192-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11269-019-2192-9

Keywords