Skip to main content

Advertisement

Springer Nature Link
Log in

A Conditional Value at Risk-Based Model for Planning Agricultural Water and Return Flow Allocation in River Systems

  • Published:
Water Resources Management Aims and scope Submit manuscript

Abstract

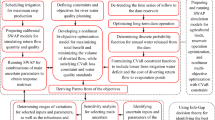
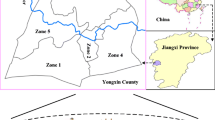
In this study, a new methodology is presented for simultaneous agricultural water and return flow (waste load) allocation in rivers. In this methodology, an objective function based on Conditional Value at Risk (CVaR) and a Nonlinear Interval Number Programming (NINP) technique are utilized. The CVaR can handle uncertainties in the form of probability distributions, while NINP incorporates uncertain inputs which are only available as intervals. This CVaR-NINP framework is used for agricultural water and return flow allocation planning under uncertainty. In this paper, to reduce the amount of saline return flow discharged into the river, a part of return flow of each agricultural network is diverted to an evaporation pond. Some meta-models based on Artificial Neural Network (ANN) are trained and validated using the results of Soil, Water, Atmosphere and Plant (SWAP) simulation model to reliably approximate the quantity and Total Dissolved Solids (TDS) load of agricultural return flows in a critical 7-day period. The effectiveness of the proposed methodology is examined through applying it to a part of Karkheh River catchment in the southwestern part of Iran. The results confirm the applicability of the model in incorporating the main uncertainties and generating water and waste load allocation policies in the form of interval numbers.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Notes

  1. Modular Simulator (MODSIM)

  2. Enhanced Stream Water Quality Model (QUAL2E)

  3. Soil and Water Assessment Tool (SWAT)

References

  • Arabi M, Govindaraju RS, Hantush MM (2006) Cost-effective allocation of watershed management practices using a genetic algorithm. Water Resour Res 42(10):W10429

    Google Scholar 

  • Artzner P, Delbaen F, Eber JM, Heath D (1999) Coherent measures of risk. Math Financ 9(3):203–228

    Article  Google Scholar 

  • Dai T, Labadie JW (2001) River basin network model for integrated water quantity/quality management. J Water Resour Plan Manag 127(5):295–305

    Article  Google Scholar 

  • Droogers P, Torabi M, Akbari M, Pazira E (2001) Field-scale modeling to explore salinity problems in irrigated agriculture. Irrig Drain 50:77–90

    Article  Google Scholar 

  • Jiang C, Han X, Liu GR, Liu GP (2008) A nonlinear interval number programming method for uncertain optimization problems. Eur J Oper Res 188(1):1–13

    Article  Google Scholar 

  • Luo B, Maqsood I, Huang GH, Yin YY, Han DJ (2005) An inexact fuzzy two-stage stochastic model for quantifying the efficiency of nonpoint source effluent trading under uncertainty. Sci Total Environ 347(1):21–34

    Article  Google Scholar 

  • Mahab Ghods Consulting Engineering Co. (2011) PayePol irrigation and drainage network: Final report

  • Mandare AB, Ambast SK, Tyagi NK, Singh J (2008) On-farm water management in saline groundwater area under scarce canal water supply condition in the Northwest India. Agric Water Manag 95:516–526

    Article  Google Scholar 

  • Nikoo MR, Kerachian R, Karimi A (2012) A nonlinear interval model for water and waste load allocations in river basins. Water Resour Manag 26(10):2911–2926

    Article  Google Scholar 

  • Nikoo MR, Kerachian R, Karimi A, Azadnia AA (2013) Optimal water and waste-load allocations in rivers using a fuzzy transformation technique: A case study. Environ Monit Assess 185(3):2483–2502

    Article  Google Scholar 

  • Nikoo MR, Kerachian R, Karimi A, Azadnia AA, Jafarzadegan K (2014) Optimal water and waste load allocation in reservoir–river systems: a case study. Environ Earth Sci 79(9):4127–4142

    Article  Google Scholar 

  • Noory H, van der Zee SEATM, Liaghat AM, Parsinejad M, van Dam JC (2011) Distributed agro-hydrological modeling with SWAP to improve water and salt management of the Voshmgir Irrigation and Drainage Network in Northern Iran. Agric Water Manag 98:1062–1070

    Article  Google Scholar 

  • Piantadosi J, Metcalfe AV, Howlett PG (2008) Stochastic dynamic programming (SDP) with a CVaR criterion for management of storm-water. J Hydrol 348:320–329

    Article  Google Scholar 

  • Poorsepahy-Samian H, Kerachian R, Nikoo MR (2012) Water and pollution discharge permit allocation to agricultural zones: Application of game theory and min-max regret analysis. Water Resour Manag 26(14):4241–4257

    Article  Google Scholar 

  • Rockafellar RT, Uryasev S (1999) Optimization of conditional value at risk. J Risk 2:21–41

    Google Scholar 

  • Rockafellar RT, Uryasev S (2002) Conditional value-at-risk for general loss distributions. J Bank Financ 26:1443–1471

    Article  Google Scholar 

  • Samipour F, Rabie M, Mohammadi K, Mahdian MH, Naseri AA (2010) Evaluation of two drainage models in south-west Iran. 9th International Drainage Symposium, Québec City, Canada

  • Shao LG, Qin XS, Xu Y (2011) A conditional value-at-risk based inexact water allocation model. Water Resour Manag 25:2125–2145

    Article  Google Scholar 

  • Singh R (2004) Simulations on direct and cyclic use of saline waters for sustaining cotton–wheat in a semi-arid area of north-west India. Agric Water Manag 66:153–162

    Article  Google Scholar 

  • Tavakoli A, Kerachian R, Nikoo MR, Soltani M, Malakpour Estalaki S (2014) Water and waste load allocation in rivers with emphasis on agricultural return flows: application of fractional factorial analysis. Environ Monit Assess 186:5935–5949

    Article  Google Scholar 

  • Tavakoli A, Nikoo MR, Kerachian R, Soltani M (2015) River water quality management considering agricultural return flows: application of a non-linear two-stage stochastic fuzzy programming. Environ Monit Assess 187:158

  • Toumazis I, Kwon C (2012) Time-dependent conditional Value-at-Risk minimization algorithm for hazardous materials routing. http://www.chkwon.net/papers/toumazis2012dcvar.pdf. Accessed 27 Dec. 2012

  • Webby RB, Boland J, Howlett P, Metcalfe AV, Sritharan T (2006) Conditional value-at-risk for water management in Lake Burley Griffin. ANZIAM J 47:116–136, EMAC2005

    Google Scholar 

  • Zhang W, Wang Y, Peng H, Li Y, Tang J, Wu B (2010) A coupled water quantity-quality model for water allocation analysis. J Water Resour Plan Manag 24(3):485–511

    Article  Google Scholar 

Download references

Acknowledgments

The authors would like to acknowledge the financial support of the University of Tehran for this research under grant number 8102060/1/07.

Author information

Authors and Affiliations

  1. School of Civil Engineering, College of Engineering, University of Tehran, Tehran, Iran

    Maryam Soltani

  2. School of Civil Engineering and Center of Excellence for Engineering and Management of Civil Infrastructures, College of Engineering, University of Tehran, Tehran, Iran

    Reza Kerachian

  3. School of Civil and Environmental Engineering, Shiraz University, Shiraz, Iran

    Mohammad Reza Nikoo

  4. Department of Irrigation and Reclamation Engineering, University of Tehran, Karaj, Iran

    Hamideh Noory

Authors
  1. Maryam Soltani
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Reza Kerachian
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Mohammad Reza Nikoo
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Hamideh Noory
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Reza Kerachian.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Soltani, M., Kerachian, R., Nikoo, M.R. et al. A Conditional Value at Risk-Based Model for Planning Agricultural Water and Return Flow Allocation in River Systems. Water Resour Manage 30, 427–443 (2016). https://doi.org/10.1007/s11269-015-1170-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11269-015-1170-0

Keywords