Skip to main content

Advertisement

Springer Nature Link
Log in

Pressure-Dependent EPANET Extension

  • Published:
Water Resources Management Aims and scope Submit manuscript

Abstract

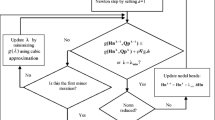
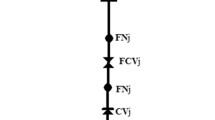
In water distribution systems (WDSs), the available flow at a demand node is dependent on the pressure at that node. When a network is lacking in pressure, not all consumer demands will be met in full. In this context, the assumption that all demands are fully satisfied regardless of the pressure in the system becomes unreasonable and represents the main limitation of the conventional demand driven analysis (DDA) approach to WDS modelling. A realistic depiction of the network performance can only be attained by considering demands to be pressure dependent. This paper presents an extension of the renowned DDA based hydraulic simulator EPANET 2 to incorporate pressure-dependent demands. This extension is termed “EPANET-PDX” (pressure-dependent extension) herein. The utilization of a continuous nodal pressure-flow function coupled with a line search and backtracking procedure greatly enhance the algorithm’s convergence rate and robustness. Simulations of real life networks consisting of multiple sources, pipes, valves and pumps were successfully executed and results are presented herein. Excellent modelling performance was achieved for analysing both normal and pressure deficient conditions of the WDSs. Detailed computational efficiency results of EPANET-PDX with reference to EPANET 2 are included as well.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22

Similar content being viewed by others

References

  • Ackley JRL, Tanyimboh TT, Tahar B, Templeman AB (2001) Head-driven analysis of water distribution systems. In: Ulanicki B, Coulbeck B, Rance J (eds) Water Software Systems: Theory and Applications, Vol. 1. Research Studies Press Ltd, England, ISBN 0863802745, Chapter 3:183–192

  • Alperovits E, Shamir U (1977) Design of optimal water distribution systems. Water Resour Res 13(6):885–900

    Article  Google Scholar 

  • Ang WH, Jowitt PW (2006) Solution for water distribution systems under pressure-deficient conditions. J Water Resour Plann Manag, ASCE 132(3):175–182

    Article  Google Scholar 

  • Bhave PR (1991) Analysis of flow in water distribution networks. Technomic Publishing, Lancaster

    Google Scholar 

  • Christodoulou SE (2010) Water network assessment and reliability analysis by use of survival analysis. Water Resour Manag 25(4):1229–1238

    Article  Google Scholar 

  • Cisty M (2010) Hybrid genetic algorithm and linear programming method for least-cost design of water distribution systems. Water Resour Manag 24(1):1–24

    Article  Google Scholar 

  • Cullinane MJ, Lansey KE, Mays LW (1992) Optimisation-availability-based design of water distribution networks. J Hydraul Eng 118(3):420–441

    Article  Google Scholar 

  • Fujiwara O, Ganesharajah T (1993) Reliability assessment of water supply systems with storage and distribution networks. Water Resour Res 29(8):2917–2924

    Article  Google Scholar 

  • Germanopoulos G (1985) A technical note on the inclusion of pressure dependent demand and leakage terms in water supply network models. Civ Eng Syst 2:171–179

    Article  Google Scholar 

  • Giustolisi O, Kapelan Z, Savic DA (2008a) Extended period simulation analysis considering valve shutdowns. J Water Resour Plann Manag 134(6):527–537

    Article  Google Scholar 

  • Giustolisi O, Savic DA, Kapelan Z (2008b) Pressure-driven demand and leakage simulation for water distribution networks. J Hydraul Eng 134(5):626–635

    Article  Google Scholar 

  • Gupta R, Bhave PR (1996) Comparison of methods for predicting deficient network performance. J Water Resour Plann Manag 122(3):214–217

    Article  Google Scholar 

  • Haghighi A, Samani HMV, Samani ZMV (2011) GA-ILP method for optimization of water distribution networks. Water Resour Manag 25(7):1791–1808

    Article  Google Scholar 

  • Jeppson RW, Davis A (1976) Pressure reducing valves in pipe network analyses. J Hydraul Div 102(HY7):987–1001

    Google Scholar 

  • Kalungi P, Tanyimboh TT (2003) Redundancy model for water distribution systems. Reliab Eng Syst Saf 82(3):275–286

    Article  Google Scholar 

  • Liberatore S, Sechi GM (2009) Location and calibration of valves in water distribution networks using a scatter-search meta-heuristic approach. Water Resour Manag 23:1479–1495

    Article  Google Scholar 

  • Martínez-Rodríguez JB, Montalvo I, Izquierdo J, Pérez-García R (2011) Reliability and Tolerance Comparison in Water Supply Networks. Water Resour Manag 25(5):1437–1448

    Article  Google Scholar 

  • OFWAT (2004) Levels of Service for the Water Industry in England and Wales. 2002–2003 Report. Ofwat Centre, 7 Hill Street, Birmingham B5 4UA, UK

  • Park S, Choi CL, Kim JH, Bae CH (2010) Evaluating the economic residual life of water pipes using the proportional hazards model. Water Resour Manag 24(12):3195–3217

    Article  Google Scholar 

  • Press WH, Teukolsky SA, Vetterling WT, Flannery BP (1992) Numerical recipes in FORTRAN: the art of scientific computing. Cambridge University Press, New York

    Google Scholar 

  • Reddy LS, Elango K (1989) Analysis of water distribution networks with head dependent outlets. Civ Eng Syst 6(3):102–110

    Article  Google Scholar 

  • Rossman LA (2002) EPANET 2 User’s Manual, Water Supply and Water Resources Division, National Risk Management Research Laboratory, Cincinnati, OH45268

  • Rossman LA (2007) Discussion of ‘Solution for water distribution systems under pressure-deficient conditions’. J Water Resour Plann Manag 133(6):566–567

    Article  Google Scholar 

  • Salgado R, Rojo J, Zepeda S (1993) Extended gradient method for fully non-linear head and flow analysis in pipe networks. Integrated Computer Applications in Water Supply—Methods and Procedures for Systems Simulation and Control 1:49–60

    Google Scholar 

  • Shan N (2004) Head dependent modelling of water distribution network. MSc Dissertation, University of Liverpool, UK

  • Siew C, Tanyimboh TT (2010a) Pressure-dependent EPANET extension: pressure-dependent demands. Proceedings of the 12th Annual Water Distribution Systems Analysis Conference, WDSA 2010, September 12–15, Tucson, Arizona

  • Siew C, Tanyimboh TT (2010b) Penalty-Free Multi-Objective Evolutionary Optimization of Water Distribution Systems. Proceedings of the 12th Annual Water Distribution Systems Analysis Conference, WDSA 2010, September 12–15, Tucson, Arizona

  • Siew C, Tanyimboh TT (2011a) The computational efficiency of EPANET-PDX. Proceedings of the 13th Annual Water Distribution Systems Analysis Conference, WDSA 2011, May 22–26, Palm Springs, California

  • Siew C, Tanyimboh TT (2011b) Design of the “Anytown” network using the penalty-free multi-objective evolutionary optimization approach. Proceedings of the 13th Annual Water Distribution Systems Analysis Conference, WDSA 2011, May 22–26, Palm Springs, California

  • Siew C, Tanyimboh TT (2011c) Penalty-free evolutionary algorithm optimization for the long term rehabilitation and upgrading of water distribution systems. Proceedings of the 13th Annual Water Distribution Systems Analysis Conference, WDSA 2011, May 22–26, Palm Springs, California

  • Tabesh M, Tanyimboh TT, Burrows R (2002) Head driven simulation of water supply networks. Int J Eng, Transactions A: Basics 15(1):11–22

    Google Scholar 

  • Tabesh M, Yekta A, Burrows R (2009) An integrated model to evaluate losses in water distribution systems. Water Resour Manag 23(3):477–492

    Article  Google Scholar 

  • Tanyimboh TT (2008) Robust algorithm for head-dependent analysis of water distribution systems. In: Van Zyl JE, Ilemobade AA, Jacobs HE (eds) Proceedings of the 10th Annual Water Distribution Systems Analysis Conference, August 17–20, Kruger National Park, South Africa

  • Tanyimboh TT, Templeman AB (2004) A new nodal outflow function for water distribution networks. In: Topping BHV, Mota Soares CA (eds) Proceedings of the 4th International Conf. on Eng. Computational Technology. Civil-Comp Press, Stirling, UK, ISBN 0-948749-98-9, Paper 64, pp. 12, CD-ROM

  • Tanyimboh TT, Templeman AB (2010) Seamless pressure-deficient water distribution system model. J Water Manag ICE 163(8):389–396

    Article  Google Scholar 

  • Tanyimboh TT, Tahar B, Templeman AB (2003) Pressure-driven modelling of water distribution systems. Water Sci Tech Water Supply 3(1–2):255–262

    Google Scholar 

  • Todini E, Pilati S (1988) A gradient algorithm for the analysis of pipe networks. In: Coulbeck B, Orr C-H (eds) Computer applications in water supply, vol 1. Research Studies Press, England

    Google Scholar 

  • Udo A, Ozawa T (2001) Steady-state flow analysis of pipe networks considering reduction of flow in the case of low water pressures. In: Ulanicki B, Coulbeck B, Rance J (eds) Water software systems: theory and applications, vol 1. Research Studies Press, Taunton, pp 73–182

    Google Scholar 

  • Wagner JM, Shamir U, Marks DH (1988) Water distribution reliability: simulation methods. J Water Resour Plann Manag 114(3):276–294

    Article  Google Scholar 

  • Walski TM, Brill ED, Gessler J, Goulter IC, Jeppson RM, Lansey K, Lee HL, Liebman JC, Mays L, Morgan DR, Ormsbee L (1987) Battle of the network models: epilogue. J Water Resour Plann Manag 113(2):191–203

    Article  Google Scholar 

  • Wu YW, Wang RH, Walski TM, Yang SY, Bowdler D, Baggett CC (2009) Extended global-gradient algorithm for pressure-dependent water distribution analysis. J Water Resour Plann Manag 135(1):13–22

    Article  Google Scholar 

  • Xu C (2001) Re: modelling demands. www.bossintl.com/forums/showthr…/threadid/5176.htm, June 2001, accessed 2002 by Tanyimboh and Templeman (2004)

Download references

Acknowledgements

This research was funded in part by the UK Engineering and Physical Sciences Research Council under Grant Number EP/G055564/1. The authors are grateful to the British Government (Overseas Research Students Award Scheme) and the University of Strathclyde for funding for the first author’s PhD programme.

Author information

Authors and Affiliations

  1. Department of Civil Engineering, University of Strathclyde Glasgow, John Anderson Building, 107 Rottenrow, Glasgow, G4 0NG, UK

    Calvin Siew & Tiku T. Tanyimboh

Authors
  1. Calvin Siew
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Tiku T. Tanyimboh
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Tiku T. Tanyimboh.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Siew, C., Tanyimboh, T.T. Pressure-Dependent EPANET Extension. Water Resour Manage 26, 1477–1498 (2012). https://doi.org/10.1007/s11269-011-9968-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11269-011-9968-x

Keywords