Network survivability modeling and analysis for power-aware MANETs by Markov regenerative processes

Abstract

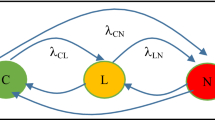
This paper presents the quantitative network survivability analysis for a power-aware mobile ad hoc network (MANET) based on Markov regenerative processes (MRGPs). The MRGP is one of the widest classes of stochastic point process which are mathematically tractable. In the past literature, the model for a power-aware MANET was described by a continuous-time Markov chain (CTMC). However, in the sense of representation ability, CTMC modeling is not sufficient to analyze the relationship between battery state and node behavior in the power-aware MANET. In particular, such problem seriously arises when we treat the transient behavior of the power-aware MANET. In the paper, we revisit a power-aware MANET model by using MRGP, and present both stationary and transient analyses for the MRGP-based model.

Appendices

A Uniformization

The uniformization approach is effective to compute the matrix exponential in the Markov analysis [21, 22]. Let $\gamma _{F,L}(v)$ and $\gamma _{L,F}(v)$ be the p.m.f.’s of mixed Poisson distribution with mixture probabilities $F_{F,L}(t)$ and $F_{L,F}(t)$, respectively:

$$\begin{aligned} \gamma _{F,L}(v)&= \int _0^\infty e^{-q_F u} \frac{(q_F u)^v}{v!} dF_{F,L}(u), \end{aligned}$$

(59)

$$\begin{aligned} \gamma _{L,F}(v)&= \int _0^\infty e^{-q_L u} \frac{(q_L u)^v}{v!} dF_{L,F}(u), \end{aligned}$$

(60)

where $q_F$ and $q_L$ are maximum values of absolute diagonal elements of $\varvec{Q}_F$ and $\varvec{Q}_L$. Using the p.m.f.’s, the matrix exponential form can be rewritten by

$$\begin{aligned} \tilde{\varvec{Q}}_F&= \sum _{v=0}^\infty \gamma _F(v) (\varvec{I}+ \varvec{Q}_F/q_F)^v, \nonumber \\ \tilde{\varvec{Q}}_L&= \sum _{v=0}^\infty \gamma _L(v) (\varvec{I}+ \varvec{Q}_L/q_L)^v, \end{aligned}$$

(61)

$$\begin{aligned} \varvec{\xi }_F&= \frac{1}{q_F} \sum _{v=0}^\infty \sum _{s=0}^v \gamma _F(v) \varvec{\pi }^{EMC}_F (\varvec{I}+ \varvec{Q}_F/q_F)^v, \end{aligned}$$

(62)

$$\begin{aligned} \varvec{\xi }_L&= \frac{1}{q_L} \sum _{v=0}^\infty \sum _{s=0}^v \gamma _L(v) \varvec{\pi }^{EMC}_L (\varvec{I}+ \varvec{Q}_L/q_L)^v, \end{aligned}$$

(63)

The infinite sums may be truncated by left truncation point $L$ and right truncation point $R$ such that

$$\begin{aligned} \sum _{v=L}^R \gamma _F(v) \ge 1 - \epsilon , \quad \sum _{v=L}^R \gamma _L(v) \ge 1 - \epsilon , \end{aligned}$$

(64)

where $\epsilon$ is a tolerance error.

B Computation of Weights

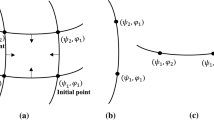
This paper utilizes the method to generate the weighted samples based on the double exponential (DE) formula [25]. This approach provides more accurate approximation to many types of integral functions, compared to trapezoidal rule, Simpson’s rule, etc. The DE formula changes the original integration to an infinite integration of the function which decays according to double exponential function. Here we use the following function

$$\begin{aligned} \phi (x) = \exp \left( \frac{\pi }{2} \sinh (x)\right) . \end{aligned}$$

(65)

By substituting the above function to $\int _0^\infty f(t) \log g(t)dt$, the integration is transformed to

$$\begin{aligned} \int _0^\infty f(t) \log g(t) dt = \int _{-\infty }^\infty f(\phi (x)) \log g(\phi (x)) \phi '(x) dx, \end{aligned}$$

(66)

where $\phi '(x)$ is the first derivative of $\phi (x)$. Applying the trapezoidal rule to the above integration, we have

$$\begin{aligned}&\int _{-\infty }^\infty f(\phi (x)) \log g(\phi (x)) \phi '(x) dx \nonumber \\&\qquad \approx \sum _{i=K^-}^{K^+} h \phi '(ih) f(\phi (ih)) \log g(\phi (ih)), \end{aligned}$$

(67)

where $h$ is a step size and $K^+ (= -K^-)$ is a upper (lower) limit of discretization points. In fact, the accuracy of integration can be controlled by the parameters $h$ and $K^+$. That is, given $h$ and $K^+$, we generate the weighted samples $(t_1, w_1), \ldots , (t_K, w_K)$ as follows

$$\begin{aligned} t_{i-K^-+1}&= \phi (ih) \end{aligned}$$

(68)

$$\begin{aligned} w_{i-K^-+1}&= h \phi '(ih) f(\phi (ih)), \nonumber \\&\qquad i = K^-, \ldots , 0, \ldots , K^+, \end{aligned}$$

(69)

where $K = K^+ - K^- + 1$.