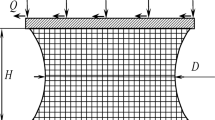
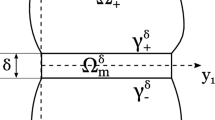
Stress-strain state components of thin-layer rubber-metal elements are investigated. The compression level of a thin rubber layer under the action of vertically applied stress is calculated. For simplified hypotheses the relationship between the rubber layer thickness reduction and its radius-thickness ratio was analytically derived. The problem was solved under linear-elastic deformation of a rubber layer vulcanized onto the metal plates. For numerical calculations, weak rubber compressibility was simulated with the moment finite element scheme for weakly compressible materials, involving the triple approximation of displacement fields, strain components, and a volume variation function. The numerical solution was obtained by the finite element method for different layer radii and thicknesses under geometrically nonlinear elastic and viscoelastic deformation of the rubber material. The geometrical nonlinearity is described by the nonlinear strain tensor. Viscoelastic rubber properties are simulated by the hereditary Boltzmann– Volterra theory with the Rabotnov relaxation kernel. Nonlinear boundary problems are solved by the modified Newton–Kantorovich method. The calculation is effected for the two cases of curing the rubber layer onto the metal elements of the structure. The first case assumes that the rubber layer is vulcanized onto the metal plates, in the second one, it can freely slide over their surface. For the first case, numerical results are compared with the analytical solution. The effect of geometrical nonlinearity and viscoelastic rubber properties on the rubber layer thickness reduction was examined.




Similar content being viewed by others
References
É. É. Levendel, Calculation of Industrial Rubber Products [in Russian], Mashinostroenie, Moscow (1976).
S. I. Dymnikov, “Calculation of industrial rubber components at medium strains,” Mekh. Polimer., No. 2, 271–275 (1968).
N. A. Sukhova and V. L. Biderman, “Calculation of rubber absorbers in compression,” Rasch. Proch., No. 8, 200–211 (1962).
V. L. Biderman and N. A. Sukhova, “Calculation of cylindrical and rectangular long rubber absorbers in compression,” Rasch. Proch., No. 13, 55–72 (1968).
V. L. Biderman and G. V. Martyanova, “Compression of low-shock rubber-metal absorbers and spacers,” Izv. AN SSSR. Ser. Mekh. Mashinostr., Issue 3, 154–158 (1962).
V. L. Biderman and G. V. Martyanova, “Compression and bending of thin-layer rubber-metal elements,” Rasch. Proch., Issue 23, 32–47 (1983).
V. I. Dyrda, A. V. Goncharenko, and L. A. Zharko, “Solution of the problem of viscoelastic cylinder compression by the Ritz method,” Geotekh. Mekh., Issue 86, 113–124 (2010).
A. F. Bulat, V. I. Dyrda, Yu. I. Nemchinov, et. al., “Vibroseismic protection of machines and constructions with rubber blocks,” Geotekh. Mekh., Issue 85, 128–132 (2010).
V. I. Dyrda, T. E. Tverdokhleb, N. I. Lisitsa, and N. N. Lisitsa, “Application of the β-method for calculating rubber-metal vibroseismic blocks,” Geotekh. Mekh., Issue 86, 144–158 (2010).
P. C. Polycarpou, P. Komodromos, and A. C. Polycarpou, “A nonlinear impact model for simulating the use of rubber shock absorbers for mitigating the effects of structural pounding during earthquakes,” Earthq. Eng. Struct. Dyn., 42, No. 1, 81–100 (2013).
M. Banić, D. Stamenković, M. Milošević, and A. Miltenović, “Tribology aspect of rubber shock absorbers development,” Tribol. Ind., 35, No. 3, 225–231 (2013).
Yu. I. Dimitrienko, S. M. Tsarev, and A. V. Veretennikov, “Elaboration of the method of finite elements from incompressible materials with large strains,” Vest. Bauman MGTU. Ser. Estestv. Nauki, No. 3, 69–82 (2007).
A. E. Belkin and D. S. Khominich, “Calculation of large strains of the arch absorber in view of triaxial rubber compressibility,” Vest. Bauman MGTU. Ser. Mashinostroenie, No. 2, 3–11 (2012).
V. I. Dyrda, S. N. Grebenyuk, and S. I. Gomenyuk, Analytical and Numerical Methods of Calculating Rubber Components [in Russian], Zaporozhye National University, Dnepropetrovsk–Zaporozhye (2012).
V. V. Kirichevskii, Finite Element Method in Mechanics of Elastomers [in Russian], Naukova Dumka, Kiev (2002).
O. C. Zienkiewicz and R. L. Taylor, The Finite Element Method, Vol. 1: The Basis, Butterworth-Heinemann, Oxford (2000).
V. N. Poturaev, V. I. Dyrda, and I. I. Krush, Applied Mechanics of Rubber [in Russian], Naukova Dumka, Kiev (1980).
A. F. Bulat, V. I. Dyrda, E. L. Zvyagilskii, and A. S. Kobets, Applied Mechanics of Elastic Hereditary Media [in Russian], in 3 volumes, Vol. 1: Mechanics of Deformation and Fracture of Elastomers, Naukova Dumka, Kiev (2011).
S. I. Dymnikov, É. É. Levendel, A. A. Pavlovskis, and M. I. Sniegs, Applied Methods of Calculating the Products from Hyperelastic Materials [in Russian], Zinatne, Riga (1980).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Problemy Prochnosti, No. 3, pp. 27 – 36, May – June, 2018.
Rights and permissions
About this article
Cite this article
Bulat, A.F., Dyrda, V.I., Lysytsya, M.I. et al. Numerical Simulation of the Stress-Strain State of Thin-Layer Rubber-Metal Vibration Absorber Elements Under Nonlinear Deformation. Strength Mater 50, 387–395 (2018). https://doi.org/10.1007/s11223-018-9982-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11223-018-9982-9