1 Introduction

Often time series are organized into a hierarchy. For example, the total visitors of a country can be divided into regions and the visitors of each region can be further divided into sub-regions. Such data structures are referred to as hierarchical time series; they are common in fields such as retail sales (Makridakis et al. 2021) and energy modelling (Taieb et al. 2021).

The forecasts for hierarchical time series should respect some summing constraints, in which case they are referred to as coherent. For instance, the sum of the forecasts for the sub-regions should match the forecast for the entire region. However, the forecasts independently produced for each time series (base forecasts) are generally incoherent.

Reconciliation algorithms (Hyndman et al. 2011; Wickramasuriya et al. 2019) adjust the incoherent base forecasts, making them coherent. Reconciled forecasts are generally more accurate than base forecasts: indeed, forecast reconciliation is a special case of forecast combination (Hollyman et al. 2021). An important application of reconciliation algorithms is constituted by temporal hierarchies (Athanasopoulos et al. 2017; Kourentzes and Athanasopoulos 2021), which make coherent the forecasts produced for the same time series at different temporal scales.

Most reconciliation algorithms (Hyndman et al. 2011; Wickramasuriya et al. 2019, 2020; Di Fonzo and Girolimetto 2021, 2022) provide only reconciled point forecasts. It is however clear (Kolassa 2023) that reconciled predictive distributions are needed for decision making.

Probabilistic reconciliation has been addressed only recently; earlier attempts (Jeon et al. 2019; Taieb et al. 2021), though experimentally effective, lacked a strong formal justification. For the case of Gaussian base forecasts, Corani et al. (2020) obtains the reconciled distribution in analytical form introducing the approach of reconciliation via conditioning. Panagiotelis et al. (2023) provides a framework for probabilistic reconciliation via projection. However this approach cannot reconcile discrete distributions. Corani et al. (2023) performs probabilistic reconciliation via conditioning of count time series by adopting the concept of virtual evidence (Pearl 1988). However its implementation in probabilistic programming, based on Markov Chain Monte Carlo (MCMC), is too slow on large hierarchies; moreover it requires the base forecast distribution to be in parametric form.

The main contribution of this paper is the Bottom-Up Importance Sampling (BUIS) algorithm, which samples from the reconciled distribution obtained via conditioning with a substantial speedup with respect to Corani et al. (2023). BUIS can be used even when the base forecast distribution is only available through samples. This is the case of forecasts returned by models for time series of counts (Liboschik et al. 2017) or based on deep learning (Salinas et al. 2020). We prove the convergence of BUIS to the actual reconciled distribution. An implementation of the algorithm in the R language is available in the R package bayesRecon (Azzimonti et al. 2023).

We provide two further formal contributions. The first is a definition of coherence for probabilistic forecasts that applies to both discrete and continuous distributions. The second is a novel interpretation of the reconciliation via conditioning, in which the base forecast distribution is conditioned on the hierarchy constraints. This allows for a unified treatment of the reconciliation of discrete and continuous forecast distributions. We test our method exhaustively on temporal hierarchies reporting positive results both for the accuracy and the efficiency of our method.

The paper is organized as follows. In Sect. 2, we introduce the notation and the reconciliation of point forecasts. In Sect. 3, we introduce our approach to reconciliation via conditioning and we compare it to the existing literature. In Sect. 4, we introduce the Bottom-Up Importance Sampling algorithm. We empirically verify its correctness in Sect. 5, while in Sect. 6 we test it on different data sets. We present the conclusions in Sect. 7.

2 Notation

Fig. 1
figure 1

A hierarchy with 4 bottom and 3 upper variables

Full size image

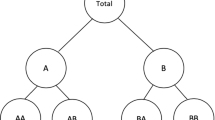
Consider the hierarchy of Fig. 1. We denote by \(\textbf{b}= [b_1,\dots ,b_{n_b}]^T\) the vector of bottom variables, and by \(\textbf{u}= [u_1,\dots ,u_{n_u}]^T\) the vector of upper variables. We then denote by

$$\begin{aligned} \textbf{y}= \begin{bmatrix} \textbf{u}\\ \textbf{b}\end{bmatrix} \in \mathbb {R}^n \end{aligned}$$

the vector of all the variables. The hierarchy can be expressed as a set of linear constraints:

(1)

\(\textbf{I}\in \mathbb {R}^{n_b \times n_b}\) is the identity matrix; we refer to \(\textbf{S}\in \mathbb {R}^{n \times n_b}\) as the summing matrix and to \(\textbf{A}\in \mathbb {R}^{n_u \times n_b}\) as the aggregating matrix. We can thus write the constraints as \(\textbf{u}= \textbf{A}\textbf{b}\). For example, the aggregating matrix of the hierarchy in Fig. 1 is:

$$\begin{aligned} A = \begin{bmatrix} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 1 \end{bmatrix}. \end{aligned}$$

A point \(\textbf{y}\in \mathbb {R}^n\) is coherent if it satisfies the constraints given by the hierarchy. We denote by \(\mathcal {S}\) the set of coherent points, which is a linear subspace of \(\mathbb {R}^n\):

$$\begin{aligned} \mathcal {S}:= \{ \textbf{y}\in \mathbb {R}^n: \; \textbf{y}= \textbf{S}\textbf{b}\}. \end{aligned}$$
(2)

2.1 Temporal hierarchies

In temporal hierarchies (Athanasopoulos et al. 2017; Kourentzes and Athanasopoulos 2021), forecasts are generated for the same time series at different temporal scales. For instance, a quarterly time series can be aggregated to the semi-annual and the annual scale. If we are interested in predictions up to one year ahead, we compute four quarterly forecasts \(\hat{q}_1, \hat{q}_2, \hat{q}_3, \hat{q}_4\), two semi-annual forecasts \(\hat{s}_1,\hat{s}_2\), and an annual forecast \(\hat{a}_1\). We then obtain the hierarchy in Fig. 1. The base point forecasts, independently computed at each frequency, are \(\hat{\textbf{b}} = [\hat{q}_1, \hat{q}_2, \hat{q}_3, \hat{q}_4]^T\) and \(\hat{\textbf{u}} = [\hat{a}_1, \hat{s}_1, \hat{s}_2]^T\).

2.2 Point forecasts reconciliation

Let us denote by \(\hat{\textbf{y}} = \big [\hat{\textbf{u}}^T\,\vert \,\hat{\textbf{b}}^T\big ]^T\) the vector of the base (incoherent) forecasts. Note that, for ease of notation, we drop the time subscript. Point reconciliation is generally performed in two steps (Hyndman et al. 2011; Wickramasuriya et al. 2019). First, the reconciled bottom forecasts are computed by linearly combining the base forecasts of the entire hierarchy:

$$\begin{aligned} \tilde{\textbf{b}} = \textbf{G}\hat{\textbf{y}}, \end{aligned}$$

for some matrix \(\textbf{G}\in \mathbb {R}^{m\times n}\). Then, the reconciled forecasts for the whole hierarchy are given by:

$$\begin{aligned} \tilde{\textbf{y}} = \textbf{S}\tilde{\textbf{b}}. \end{aligned}$$

The state-of-the-art reconciliation method is MinT (Wickramasuriya et al. 2019), which defines \(\textbf{G}\) as:

$$\begin{aligned} \textbf{G}= (\textbf{S}^T \textbf{W}^{-1} \textbf{S})^{-1} \textbf{S}^T \textbf{W}^{-1}, \end{aligned}$$

where \(\textbf{W}\) is the covariance matrix of the errors of the base forecasts. This method minimizes the expected sum of the squared errors of the reconciled forecasts, under the assumption of unbiased base forecasts.

2.3 Probabilistic framework

Probabilistic reconciliation requires a probabilistic framework, in which forecasts are in the form of probability distributions. We denote by \(\hat{\nu } \in \mathcal {P}(\mathbb {R}^n)\) the forecast distribution for \(\textbf{y}\), where \(\mathcal {P}(\mathbb {R}^n)\) is the space of probability measures on \(\left( \mathbb {R}^n, \mathcal {B}(\mathbb {R}^n)\right) \), and \(\mathcal {B}(\mathbb {R}^n)\) is the Borel \(\sigma \)-algebra on \(\mathbb {R}^n\). Moreover, we denote by \(\hat{\nu }_u\) and \(\hat{\nu }_b\) the marginal distributions of, respectively, the forecasts for the upper and the bottom components of \(\textbf{y}\).

The forecast distribution \(\hat{\nu }\) may be either discrete or absolutely continuous. In the following, if there is no ambiguity, we will use \(\hat{\pi }\) to denote either its probability mass function, in the former case, or its density, in the latter. Therefore, if \(\hat{\nu }\) is discrete, we have

$$\begin{aligned} \hat{\nu }(F) = \sum _{x \in F} \hat{\pi }(x), \end{aligned}$$

for any \(F \in \mathcal {B}(\mathbb {R}^n)\). Note that the sum is well-defined as \(\hat{\pi }(x) > 0\) for at most countably many x’s. On the contrary, if \(\hat{\nu }\) is absolutely continuous, for any \(F \in \mathcal {B}(\mathbb {R}^n)\) we have

$$\begin{aligned} \hat{\nu }(F) = \int _F \hat{\pi }(x) \, dx. \end{aligned}$$

3 Probabilistic Reconciliation

We now discuss coherence in the probabilistic framework and our approach to probabilistic reconciliation.

Recall that a point forecast is incoherent if it does not belong to the set \(\mathcal {S}\), defined as in (2). Let \(\hat{\nu } \in \mathcal {P}(\mathbb {R}^n)\) be a forecast distribution. Intuitively, \(\hat{\nu }\) is incoherent if there exists a set T of incoherent points, i.e. \(T \cap \mathcal {S} = \emptyset \), such that \(\hat{\nu }(T) > 0\). Or, equivalently, if \(supp(\hat{\nu }) \nsubseteq \mathcal {S}\). We now define the summing map \(s: \mathbb {R}^{n_b} \rightarrow \mathbb {R}^n\) as

$$\begin{aligned} s(\textbf{b}) = \textbf{S}\textbf{b}. \end{aligned}$$
(3)

The image of s is given by \(\mathcal {S}\). Moreover, from (3) and (1), s is injective. Hence, s is a bijective map between \(\mathbb {R}^{n_b}\) and \(\mathcal {S}\), with inverse given by \(s^{-1}(\textbf{y}) = \textbf{b}\), where \(\textbf{y}= (\textbf{u}, \textbf{b}) \in \mathcal {S}\). As explained in Panagiotelis et al. (2023), for any \(\nu \in \mathcal {P}(\mathbb {R}^{n_b})\) we may obtain a distribution \(\tilde{\nu }\in \mathcal {P}(\mathcal {S})\) as \(\tilde{\nu }= s_{\#} \nu \), namely the pushforward of \(\nu \) using s:

$$\begin{aligned} \tilde{\nu }(F) = \nu (s^{-1}(F)), \qquad \forall \, F \in \mathcal {B}(\mathcal {S}), \end{aligned}$$

where \(s^{-1}(F):= \{ \textbf{b} \in \mathbb {R}^{n_b}: s(\textbf{b}) \in F \}\) is the preimage of F. In other words, \(s_{\#}\) builds a probability distribution for \(\textbf{y}\) supported on the coherent subspace \(\mathcal {S}\) from a distribution on the bottom variables \(\textbf{b}\). Since s is a measurable bijective map, \(s_{\#}\) is a bijection between \(\mathcal {P}(\mathbb {R}^{n_b})\) and \(\mathcal {P}(\mathcal {S})\), with inverse given by \((s^{-1})_{\#}\) (Appendix A). We thus propose the following definition.

Definition 1

We call coherent distribution any distribution \(\nu \in \mathcal {P}(\mathbb {R}^{n_b})\).

This definition works with any type of distribution. Moreover, it can be used even if the constraints are not linear, as it does not require s to be a linear map.

3.1 Probabilistic reconciliation

The aim of probabilistic reconciliation is to obtain a coherent reconciled distribution \(\tilde{\nu }\in \mathcal {P}(\mathbb {R}^{n_b})\) from the base forecast distribution \(\hat{\nu } \in \mathcal {P}(\mathbb {R}^n)\).

The probabilistic bottom-up approach, which simply ignores any probabilistic information about the upper series, is obtained by setting \(\tilde{\nu }= \hat{\nu }_b\).

Panagiotelis et al. (2023) proposes a reconciliation method based on projection. Given a continuous map \(\psi : \mathbb {R}^n \rightarrow \mathcal {S}\), the reconciled distribution \(\tilde{\nu } \in \mathcal {P}(\mathcal {S})\) is defined as the push-forward of the base forecast distribution \(\hat{\nu }\) using \(\psi \):

$$\begin{aligned} \tilde{\nu } = \psi _{\#} \hat{\nu }, \end{aligned}$$

i.e. \(\tilde{\nu }(F) = \hat{\nu }(\psi ^{-1}(F))\), for any \(F \in \mathcal {B}(\mathbb {R}^n)\). Hence, if \(\textbf{y}_1, \dots , \textbf{y}_N\) are independent samples from \(\hat{\nu }\), then \(\psi (\textbf{y}_1), \dots ,\)\( \psi (\textbf{y}_N)\) are independent samples from \(\tilde{\nu }\). The map \(\psi \) is expressed as \(\psi = s \circ g\), where \(g: \mathbb {R}^n \rightarrow \mathbb {R}^{n_b}\) combines information from all the levels by projecting on the bottom level. g is assumed to be in the form \(g(\textbf{y}) = \textbf{d} + \textbf{G}\textbf{y}\), and the parameters \(\mathbf {\gamma }:= (\textbf{d}, \textit{vec}(\textbf{G})) \in \mathbb {R}^{n_b + n_b \times n}\) are optimized through stochastic gradient descent (SGD) to minimize a chosen scoring rule. This approach therefore can only be used with continuous distributions.

3.2 Probabilistic Reconciliation through conditioning

We now present our approach to probabilistic reconciliation, based on conditioning on the hierarchy constraints. Let \(\hat{\textbf{Y}}= (\hat{\textbf{U}},\hat{\textbf{B}})\) be a random vector representing the probabilistic forecasts with distribution given by \(\hat{\nu }\), so that \(\hat{\nu }_u\) and \(\hat{\nu }_b\) are the distributions of \(\hat{\textbf{U}}\) and \(\hat{\textbf{B}}\).

Let us first suppose that the base forecast distribution \(\hat{\nu } \in \mathcal {P}(\mathbb {R}^n)\) is discrete, and let \(\hat{\pi }\) be its probability mass function. We define \(\tilde{\nu }\) by conditioning on the coherent subspace \(\mathcal {S}\):

$$\begin{aligned} \tilde{\nu }(F)&= \mathbb {P}(\hat{\textbf{B}}\in F \mid \hat{\textbf{Y}}\in \mathcal {S}) \nonumber \\&= \frac{ \mathbb {P}(\hat{\textbf{B}}\in F,\, \hat{\textbf{Y}}\in \mathcal {S}) }{\mathbb {P}(\hat{\textbf{Y}}\in \mathcal {S})} \nonumber \\&= \frac{ \mathbb {P}(\hat{\textbf{B}}\in F,\, \hat{\textbf{U}}= \textbf{A}\hat{\textbf{B}}) }{\mathbb {P}(\hat{\textbf{U}}= \textbf{A}\hat{\textbf{B}})} \nonumber \\&= \frac{\sum _{\textbf{b}\in F} \hat{\pi }(\textbf{A}\textbf{b}, \textbf{b})}{\sum _{\textbf{x}\in \mathbb {R}^{n_b}} \hat{\pi }(\textbf{A}\textbf{x}, \textbf{x})}, \end{aligned}$$
(4)

for any \(F \in \mathcal {B}(\mathbb {R}^{n_b})\), provided that \(\mathbb {P}(\hat{\textbf{Y}}\in \mathcal {S}) > 0\). The sums in (4) are well-defined, as \(\hat{\pi }(\textbf{u},\textbf{b})=\hat{\pi }(\textbf{y}) > 0\) for at most countably many \(\textbf{y}\)’s. Hence, \(\tilde{\nu }\) is a discrete probability distribution with pmf given by

$$\begin{aligned} \tilde{\pi }(\textbf{b}) = \frac{\hat{\pi }(\textbf{A}\textbf{b}, \textbf{b})}{\sum _{\textbf{x}\in \mathbb {R}^{n_b}} \hat{\pi }(\textbf{A}\textbf{x}, \textbf{x})} \propto \hat{\pi }(\textbf{A}\textbf{b},\textbf{b}). \end{aligned}$$
(5)

Note that, if \(\hat{\nu }\) is absolutely continuous, we have that \(\hat{\nu }(\mathcal {S}) = 0\), since the Lebesgue measure of \(\mathcal {S}\) is zero. Hence, \(\mathbb {P}(\hat{\textbf{B}}\in F \mid \hat{\textbf{Y}}\in \mathcal {S})\) is not well-defined. However, if we denote by \(\hat{\pi }\) the density of \(\hat{\nu }\), the last expression is still well-posed. We thus give the following definition.

Definition 2

Let \(\hat{\nu } \in \mathcal {P}(\mathbb {R}^n)\) be a base forecast distribution. The reconciled distribution through conditioning is defined as the probability distribution \(\tilde{\nu } \in \mathcal {P}(\mathbb {R}^{n_b})\) such that

$$\begin{aligned} \tilde{\pi }(\textbf{b}) \propto \hat{\pi }(\textbf{A}\textbf{b},\textbf{b}), \end{aligned}$$
(6)

where \(\hat{\pi }\) and \(\tilde{\pi }\) are the densities of (respectively) \(\hat{\nu }\) and \(\tilde{\nu }\), if \(\hat{\nu }\) is absolutely continuous, or the probability mass functions otherwise.

To rigorously derive (6) in the continuous case, we proceed as follows. Let us define the random vector \(\textbf{Z}:= \hat{\textbf{U}}- \textbf{A}\hat{\textbf{B}}\). Note that the event \(\{\hat{\textbf{Y}}\in \mathcal {S}\}\) coincides with \(\{\textbf{Z}= {\textbf {0}}\}\). The joint density of \((\textbf{Z},\hat{\textbf{B}})\) can be easily computed (Appendix A):

$$\begin{aligned} \pi _{(\textbf{Z},\hat{\textbf{B}})}(\textbf{z},\textbf{b}) = \hat{\pi }(\textbf{z}+ \textbf{A}\textbf{b}, \textbf{b}). \end{aligned}$$

Then, the conditional density of \(\hat{\textbf{B}}\) given \(\textbf{Z}= {\textbf {0}}\) is given by (Çinlar 2011, Chapter 4):

$$\begin{aligned} \tilde{\pi }(\textbf{b})&= \frac{\pi _{(Z,B)}({\textbf {0}},\textbf{b})}{\int _{\mathbb {R}^{n_b}} \pi _{(Z,B)}({\textbf {0}},\textbf{x}) \, d\textbf{x}} \\&= \frac{\hat{\pi }(\textbf{A}\textbf{b}, \textbf{b})}{\int _{\mathbb {R}^{n_b}} \hat{\pi }(\textbf{A}\textbf{x}, \textbf{x}) \, d\textbf{x}} \\&\propto \hat{\pi }(\textbf{A}\textbf{b}, \textbf{b}), \end{aligned}$$

provided that \(\int _{\mathbb {R}^{n_b}} \hat{\pi }(\textbf{A}\textbf{x}, \textbf{x}) \, d\textbf{x}> 0\). Finally, note that, if \(\hat{\textbf{U}}\) and \(\hat{\textbf{B}}\) are independent, (6) may be rewritten as

$$\begin{aligned} \tilde{\pi }(\textbf{b}) \propto \hat{\pi }_u(\textbf{A}\textbf{b}) \cdot \hat{\pi }_b(\textbf{b}), \end{aligned}$$
(7)

where \(\hat{\pi }_u\) and \(\hat{\pi }_b\) are the densities of (respectively) \(\hat{\nu }_u\) and \(\hat{\nu }_b\). This approach can be applied to both continuous and discrete distributions, yielding the same expression (6) for the reconciled distribution.

Given two coherent points \(\textbf{y}_1, \textbf{y}_2 \in \mathcal {S}\), the distribution reconciled through conditioning satisfies the following property:

$$\begin{aligned} \frac{\tilde{\pi }(\textbf{y}_1)}{\tilde{\pi }(\textbf{y}_2)} = \frac{\hat{\pi }(\textbf{y}_1)}{\hat{\pi }(\textbf{y}_2)} \end{aligned}$$
(8)

if \(\hat{\pi }(\textbf{y}_2) \ne 0\), and \(\tilde{\pi }(\textbf{y}_2) = 0\) if \(\hat{\pi }(\textbf{y}_2) = 0\); i.e., the relative probabilities of the coherent points are preserved. Moreover, reconciliation via conditioning ignores the behaviour of the base distribution outside the coherent subspace. As shown by (6), \(\tilde{\nu }\) only depends on the values of \(\hat{\nu }\) on \(\mathcal {S}\). Reconciliation via conditioning is therefore invariant under modifications of the base forecast probabilities outside the coherent subspace. This constitutes a major difference with respect to the method of Panagiotelis et al. (2023) that will be thoroughly studied in future work.

In Corani et al. (2023), the authors follow an approach based on virtual evidence (Pearl 1988) to reconcile discrete forecasts. They set the joint bottom-up distribution as a prior on the entire hierarchy, and the update is made by conditioning on the base upper forecasts, treated as uncertain observations. In contrast, we provide a unified treatment of reconciliation via conditioning for the discrete and the continuous case. Our approach has a clear interpretation, as the conditioning is done on the hierarchy constraints.

4 Sampling from the reconciled distribution

If the base forecasts are jointly Gaussian, then the reconciled distribution is also Gaussian. In this case, reconciliation via conditioning yields the same mean and variance (Corani et al. 2020) of MinT, which is optimal with respect to the log score (Wickramasuriya 2023).

In general, however, the reconciled distribution is not available in parametric form, hence we need to resort to sampling approaches. We propose a method based on Importance Sampling (IS, Kahn 1950; Elvira and Martino 2021).

4.1 Importance Sampling

Let X be an absolutely continuous random variable with density p. Suppose we want to compute the expectation \(\mu = \mathbb {E}[f(X)]\), for some function f. Importance Sampling estimates the expectation \(\mu \) by sampling from a different distribution q, and by weighting the samples to correct the mismatch between the target p and the proposal q.

In the following the term density denotes either the probability mass function (for discrete distributions) or the density with respect to the Lebesgue measure (for absolutely continuous distributions). Let q be a density such that \(q(x)>0\) if \(f(x) p(x) \ne 0\), and let \(y_1,\dots ,y_N\) be independent samples drawn from q. The self-normalized importance sampling estimate (Elvira and Martino 2021) is:

$$\begin{aligned} \mathbb {E}[f(X)] \approx \frac{\sum _{i=1}^N w(y_i) f(y_i)}{\sum _{i=1}^N w(y_i)}, \end{aligned}$$
(9)

where w is defined as \(w(y) = c \, \frac{p(y)}{q(y)}\), for some (typically unknown) constant c.

4.2 Probabilistic reconciliation via IS

Let \(\tilde{\nu }\) (Definition 2) be the target distribution. We set \(\hat{\nu }_b\) as proposal distribution. Given a sample \(\textbf{b}_1,\dots ,\textbf{b}_N\) drawn from \(\hat{\nu }_b\), the weights are computed as

$$\begin{aligned} w_i:= \frac{\hat{\pi }(\textbf{A}\textbf{b}_i, \textbf{b}_i)}{\hat{\pi }_b(\textbf{b}_i)}. \end{aligned}$$
(10)

Then, \((\textbf{b}_i, \tilde{w}_i)_{i=1,\dots ,N}\) is a weighted sample from \(\tilde{\nu }\), where \(\tilde{w}_i:= \nicefrac {w_i}{\sum _{j=1}^N w_j}\) are the normalized weights. Note that (10) may be interpreted as the conditional density of \(\hat{\textbf{U}}\) at the point \(\textbf{A}\textbf{b}_i\), given that \(\hat{\textbf{B}}= \textbf{b}_i\). We thus draw samples \((\textbf{b}_i)_i\) from the base bottom distributions, and then weight how likely they are using the base upper distributions. Under the assumption of independence between \(\hat{\textbf{B}}\) and \(\hat{\textbf{U}}\), the density of \(\tilde{\nu }\) factorizes as in (7), hence:

$$\begin{aligned} w_i = \hat{\pi }_u(\textbf{A}\textbf{b}_i). \end{aligned}$$
(11)

However, IS is affected by the curse of dimensionality (Agapiou et al. 2017). In Appendix D.2, we empirically show that IS has poor accuracy when reconciling large hierarchies. Another shortcoming of IS is that it is unreliable if the proposal distribution does not well approximate the target distribution. Indeed, we prove in Appendix E that the performance of IS degrades as the Kullback–Leibler divergence between bottom-up and base forecast distributions (which is related to the incoherence of the base forecasts) increases. The Bottom-Up Importance Sampling (BUIS) algorithm addresses such problems.

4.3 Bottom-Up Importance Sampling algorithm

Algorithm 1
figure a

Bottom-Up Importance Sampling

Full size image

First, we state the main assumption of our algorithm:

Assumption 1

The base forecasts of each variable are conditionally independent, given the time series observations.

We leave for future work the extension of this algorithm to deal with correlations between the base forecasts. In this paper we perform experiments with temporal hierarchies, which commonly make this assumption.

In order to simplify the presentation, we also assume that the data structure is strictly hierarchical, i.e., that every node only has one parent and thus the hierarchy is represented by a tree. Grouped time series (Hyndman and Athanasopoulos 2021, Chapter 11), which do not satisfy this assumption, require a more complex treatment; we discuss it in Sect. 4.5.

The BUIS algorithm exploits the hierarchical structure to split a large \(n_u\)-dimensional importance sampling problem into \(n_u\) one-dimensional problems, thus deeply alleviating the curse of dimensionality. BUIS starts by drawing a sample from the base bottom distribution \(\hat{\nu }_b\). Then, for each level of the hierarchy, from bottom to top, it updates the sample through an importance sampling step, using the “partially” reconciled distribution as proposal.

For each level \(l=1,\dots ,L\) of the hierarchy, we denote the upper variables at level l by \(u_{1,l}, \dots ,u_{k_l, l}\). Moreover, for any upper variable \(u_{j, l}\), we denote by \(b_{1, (j,l)}, \dots , b_{q_{j,l}, (j,l)}\) the bottom variables that sum up to \(u_{j, l}\). In this way, we have that \(\sum _{l=1}^L k_l = n_u\), the number of upper variables, while \(\sum _{j=1}^{k_l} q_{j,l} = n_b\), the number of bottom variables, for each level l.

Let us consider, for example, the hierarchy in Fig. 1. For the first level \(l=1\), we have \(k_1 = 2\), \(u_{1,1} = U_2\), and \(u_{2,1} = U_3\). Moreover, \(q_{1,1} = q_{2,1} = 2\), and \(b_{1, (1,1)} = B_1\), \(b_{2, (1,1)} = B_2\), \(b_{1, (2,1)} = B_3\), \(b_{2, (2,1)} = B_4\). For the last level \(l=2\), we have \(k_2 = 1\), \(u_{1,2} = U_1\), \(q_{1,2} = 4\), \(b_{1, (1,2)} = B_1\), \(b_{2, (1,2)} = B_2\), \(b_{3, (1,2)} = B_3\), \(b_{4, (1,2)} = B_4\).

Alg. 1 shows the BUIS algorithm. The “Resample” step samples with replacement from the discrete distribution given by

$$\begin{aligned} \mathbb {P}\left( \textbf{b}= \left( b^{(i)}_{1, (j,l)}, \dots , b^{(i)}_{q_{j,l}, (j,l)} \right) \right) = w^{(i)}, \end{aligned}$$
(12)

for all \(i = 1, \dots , N\). Note that the algorithm can be easily parallelized by drawing batches of samples on different cores. This additional step would further reduce the computational times.

We explicit the BUIS algorithm on the simple hierarchy in Fig. 1:

  1. 1.

    Sample \((b_j^{(i)})_{i=1,\dots ,N}\) from \(\pi _{B_j}\), for \(j=1,2,3,4\)

  2. 2.

    Compute the weights \((w^{(i)})_{i=1,\dots ,N}\) with respect to \(U_2\) as

    $$\begin{aligned}w^{(i)} = \pi _{U_2}\left( b_1^{(i)} + b_2^{(i)} \right) \end{aligned}$$
  3. 3.

    Sample \(\left( \bar{b}_1^{(i)}, \bar{b}_2^{(i)}\right) _i\) with replacement from \(\left( (b_1^{(i)}, b_2^{(i)}),\right. \)\(\left. w^{(i)} \right) _{i=1,\dots ,N}\)

  4. 4.

    Repeat step 2 and 3 using \(B_3, B_4\) and \(U_3\) to get \(\left( \bar{b}_3^{(i)}, \bar{b}_4^{(i)}\right) _i\)

  5. 5.

    Set \(\left( b_1^{(i)}, b_2^{(i)}, b_3^{(i)}, b_4^{(i)}\right) _i = \left( \bar{b}_1^{(i)}, \bar{b}_2^{(i)}, \bar{b}_3^{(i)}, \bar{b}_4^{(i)}\right) _i\) and move to the next level

  6. 6.

    Compute the weights \((w^{(i)})_{i=1,\dots ,N}\) with respect to \(U_1\) as

    $$\begin{aligned}w^{(i)} = \pi _{U_1}\left( b_1^{(i)} + b_2^{(i)} + b_3^{(i)} + b_4^{(i)} \right) \end{aligned}$$
  7. 7.

    Sample \(\left( \bar{b}_1^{(i)}, \bar{b}_2^{(i)}, \bar{b}_3^{(i)}, \bar{b}_4^{(i)} \right) _i\) with replacement from \(\left( (b_1^{(i)}, b_2^{(i)}, b_3^{(i)}, b_4^{(i)}), w^{(i)} \right) _i\)

In Appendix B we prove the following proposition:

Proposition 1

The output of the BUIS algorithm is approximately a sample drawn from the reconciled distribution \(\tilde{\nu }\).

4.4 Sample-based BUIS

Sometimes the base forecasts are given as samples, without a parametric form; this is the case of models for time series of counts (Liboschik et al. 2017) or based on deep learning (Salinas et al. 2020). BUIS can reconcile also this type of base forecasts. Since we only deal with one-dimensional densities to compute the weights, we use approximations based on samples. For discrete distributions, we use the empirical distribution. For continuous distributions, we use kernel density estimation (Chen 2017). Therefore, we only need to replace line 4 in Algorithm 1 with:

figure b

The sample-based algorithm becomes slightly slower due to the density estimation step.

4.5 More complex hierarchies: grouped time series

We refer to grouped time series when the data structure does not disaggregate in a unique hierarchical manner (Hyndman and Athanasopoulos 2021, Chapter 11). In this case, the aggregated series cannot be represented by a single tree, as a bottom node can have more than one parent. For instance, consider a weekly time series, for which we compute the following temporal aggregates: 2-weeks, 4-weeks, 13-weeks, 26-weeks, 1-year. A bottom node (weekly) is thus children of both the 2-weeks and of the 13-weeks aggregates. This structure cannot be represented as a tree.

The BUIS algorithm, as described in Sect. 4.3, requires that the hierarchy is a tree, so it cannot be used in this case. Indeed, as highlighted in the proof, we need the independence of \(\bar{\textbf{b}}_1, \dots , \bar{\textbf{b}}_{k_l}\) to multiply their densities. If the hierarchy is not a tree, correlations between bottom variables are created when conditioning on the upper levels.

To overcome this problem, we proceed as follows. First, we find the largest sub-hierarchy within the group structure. For instance, in the example above, we consider the sub-hierarchy given by the bottom variables and by the 2-weeks, 4-weeks and 1-year aggregates. All the other upper variables are then regarded as additional constraints. We use the BUIS algorithm on the sub-hierarchy, obtaining a sample \(\textbf{b}\). Then, we compute the weights on \(\textbf{b}\) using the base distributions of the additional constraints. This is equivalent to performing a standard IS, where we use the output of BUIS on the hierarchical part as proposal distribution. In this way, we reduce the dimension of the IS task from \(n_u\), the total number of upper constraints, to the number of constraints that are not included in the sub-hierarchy: in the above example, from 46 to 6. We highlight that the distribution we sample from would be the same even with different choices of sub-hierarchies. However, picking the largest one is the best choice from a computational perspective.

5 Experiments on synthetic data

Fig. 2
figure 2

A binary hierarchy

Full size image
Fig. 3
figure 3

Wasserstein distance between true and empirical distributions. The axes are logarithmic

Full size image

We now empirically test the convergence of the BUIS algorithm to the true reconciled distribution. We compare BUIS with IS and with the method by Corani et al. (2023), which we implement using the library PyMC (Salvatier et al. 2016). PyMC adopts an adaptive Metropolis-Hastings algorithm (Haario et al. 2001) for discrete distributions and the No-U-Turn Sampler (NUTS, Hoffman and Gelman 2014) for continuous distributions. We performed experiments on the hierarchy of Fig. 2, implementing the IS and BUIS algorithms in Python.

5.1 Reconciling Gaussian forecasts

Dealing with Gaussian base forecasts, the reconciled distribution can be obtained in closed form (Corani et al. 2020). We can thus check how the various algorithms approximates the exact solution. We set on each bottom node a Gaussian distribution with mean randomly chosen in the interval [5, 10], and standard deviation \(\sigma _b = 2\). We denote by \(\varvec{\mu }_b \in \mathbb {R}_+^8\) the vector of the base bottom means. We induce incoherence by setting the means of the base forecast of the upper variables as \(\varvec{\mu }_u = (1+\epsilon ) \textbf{A}\varvec{\mu }_b\), where \(\textbf{A}\) is the aggregating matrix and \(\epsilon \) is the incoherence level; we consider \(\epsilon \in \{ 0.1, \; 0.3, \, 0.5 \}\). Hence, if \(\epsilon \) =0.3 the base upper means are \(30\%\) greater than the sum of the corresponding base bottom means. We set \(\sigma _u = 3\) as standard deviation for the base forecast of each upper variable.

We run PyMC with 4 chains with 5, 000 samples each. For IS and BUIS, we run multiple experiments, drawing each time a different number of samples, ranging from \(10^4\) to \(10^6\). We repeat each experiment 30 times. We then compute the 2-Wasserstein distance (Panaretos and Zemel 2019) between the true reconciled distribution, obtained analytically, and the empirical distributions obtained via sampling. The results are reported in Fig. 3a, where we also show the \(95\%\) confidence interval over the 30 experiments. Note that the axes are in logarithmic scale.

As expected, the performance of IS and BUIS depends on the incoherence level \(\epsilon \). This behavior also affects BUIS, which is based on importance sampling. However, BUIS is significantly more robust than IS, and it works effectively even with extreme incoherence level such as \(\epsilon = 0.5\). As the number of samples grows, the performance of BUIS improves, eventually outperforming the reference method based on PyMC. We confirm the results by computing the percentage error on the reconciled mean (Appendix D.1). Even with an extreme incoherence level, \(\epsilon = 0.5\), the percentage error on the mean obtained with \(10^6\) samples from BUIS is negligible (\(<0.1\%\)) and comparable to PyMC. In the same setup IS achieves an error greater than \(5\%\).

Both IS and BUIS are substantially faster than PyMC (Table 1). The computational time of BUIS with \(10^5\) samples is two orders of magnitude smaller than PyMC, while achieving comparable performances. Note that here BUIS is running on a single core. An insight about the reasons of such a speedup is given in Appendix C, where we provide a detailed comparison between IS and a bare-bones implementation of MCMC on a simple hierarchy.

We also conduct similar experiments using a larger hierarchy; the results, reported in Appendix D.2, confirm that the BUIS is robust and computationally efficient.

Table 1 Average computational times with the standard deviations (in seconds). The average times for PyMC (4 chains with 5, 000 samples each) are: 26.81 ± 2.38 (Gaussian), 26.26 ± 4.14 (Poisson)
Full size table

5.2 Reconciling Poisson forecasts

We now consider discrete base forecasts. We set a Poisson distribution on each bottom variable, with mean randomly chosen in the interval [5, 10]. We denote by \(\varvec{\lambda }_b \in \mathbb {R}_+^8\) the vector of the base bottom means. As before, for each incoherence level \(\epsilon \in \{0.1, \; 0.3, \; 0.5\}\), we set the mean of the upper variables as \(\varvec{\lambda }_u = (1+\epsilon ) \textbf{A}\varvec{\lambda }_b\). In the Poisson case, the reconciled distribution cannot be analytically computed. We thus run an extensive experiment using PyMC, with 20 chains with 50, 000 samples each. We consider these samples as the true reconciled distribution.

We run the same experiments described in Sect. 5.1. Since probabilistic forecasts of count time series are typically given as samples (Liboschik et al. 2017), we also run sample-based BUIS (Sect. 4.4): we assume that the parametric form of the base distribution is unknown, and that only samples are available.

The 2-Wasserstein distances are reported in Fig. 3b. As the number of samples grows, BUIS and sample-based BUIS eventually outperform PyMC, for all levels of incoherence. As for the Gaussian case, the performance of IS deteriorates for larger values of the incoherence level. The results are confirmed by the percentage error on the reconciled mean (Appendix D.1), which is lower than \(0.2\%\) for BUIS with \(10^5\) samples and about \(0.4\%\) for PyMC.

In Table 1 we show the average computational times. Sample-based BUIS is slightly slower than BUIS because of the density estimation step. Note that, using \(10^5\) samples, BUIS and sample-based BUIS are 2 orders of magnitude faster than PyMC, while achieving a better performance for all incoherence levels.

6 Experiments on real data

We now perform probabilistic reconciliation on temporal hierarchies, using time series extracted from two different data sets: carparts, available from the R package expsmooth (Hyndman 2018), and syph, available from the R package ZIM (Yang et al. 2018).

The carparts data set is about monthly sales of car parts. As in (Hyndman et al. 2008, Chapter 16), we remove time series with missing values, with less then 10 positive monthly demands and with no positive demand in the first 15 and final 15 months. After this selection, there are 1046 time series left. Note that we use less restrictive criteria in the selection of the time series than Corani et al. (2023), where only 219 time series from carparts were considered. Monthly data are aggregated into 2-months, 3-months, 4-months, 6-months and 1-year levels.

The syph data set is about the weekly number of syphilis cases in the United States. We remove the time series with ADI greater than 20. The ADI is computed as \(ADI= \frac{\sum _{i=1}^P p_i}{P}\), where \(p_i\) is the time period between two non-zeros values and P is the total number of periods (Syntetos and Boylan 2005). We also remove the time series corresponding to the total number of cases in the US. After this selection, there are 50 time series left. Weekly data are aggregated into 2-weeks, 4-weeks, 13-weeks, 26-weeks and 1-year levels.

For both data sets, we fit a generalized linear model with the tscount package (Liboschik et al. 2017). We use a negative binomial predictive distribution, with a first-order regression on past observations. The test set has length 1 year for both data sets. We thus compute up to 12 steps ahead at monthly level, and up to 52 steps ahead at weekly level. Probabilistic forecasts are returned in the form of samples.

Table 2 Skill scores on the time series extracted from carparts, detailed by each level of the hierarchy
Full size table

Reconciliation is performed in three different ways. In the first case, we fit a Gaussian distribution on the returned samples. Then, we follow (Corani et al. 2020) to analytically compute the Gaussian reconciled distribution. In the second case, we fit a negative binomial distribution on the samples, and we reconcile using the BUIS algorithm. Since these are grouped time series rather than hierarchical time series, we use the method of Sect. 4.5 for grouped time series. Finally, we use the sample-based BUIS (Sect. 4.4), without fitting a parametric distribution. Although the sample-based algorithm is slightly slower, this method yields a computational gain over BUIS, as fitting a negative binomial distribution on the samples requires about 1.2 s for the monthly hierarchy and 3.9 s for the weekly hierarchy. We refer to these methods, respectively, as N, NB, and samples. Furthermore, we denote by base the unreconciled forecasts.

Table 3 Skill scores on the time series extracted from syph, detailed by each level of the hierarchy
Full size table

We use different indicators to assess the performance of each method. The mean scaled absolute error (MASE) (Hyndman 2006) is defined as

$$\begin{aligned} \text {MASE} = \frac{\text {MAE}}{Q}, \end{aligned}$$

where \(\text {MAE} = \frac{1}{h} \sum _{j=1}^h |y_{t+j} - \hat{y}_{t+j\mid t}|\) and \(Q = \frac{1}{T-1} \sum _{t=2}^T\)\( |y_t - y_{t-1}|\). Here, \(y_t\) denotes the value of the time series at time t, while \(\hat{y}_{t+j\mid t}\) denotes the point forecast computed at time t for time \(t+j\). The median of the distribution is used as point forecast, since it minimizes MASE (Kolassa 2016).

The mean interval score (MIS) (Gneiting 2011) is defined, for any \(\alpha \in (0,1)\), as

$$\begin{aligned} \text {MIS} = (u - l) + \frac{2}{\alpha } (l - y) \mathbbm {1}(y<l) + \frac{2}{\alpha } (y-u) \mathbbm {1}(y>u), \end{aligned}$$

where l and u are the lower and upper bounds of the \((1-\alpha )\) forecast coverage interval and y is the actual value of the time series. In the following, we use \(\alpha = 0.1\). MIS penalizes wide prediction intervals, as well as intervals that do not contain the true value.

Finally, the Energy score (Székely and Rizzo 2013) is defined as

$$\begin{aligned} ES(P,\textbf{y}) = \mathbb {E}_P\left[ \Vert \textbf{y}-\textbf{s}\Vert ^{\alpha }\right] - \frac{1}{2} \mathbb {E}_P\left[ \Vert \textbf{s}-\textbf{s}'\Vert ^{\alpha }\right] , \end{aligned}$$

where P is the forecast distribution on the whole hierarchy, \(\textbf{s}, \textbf{s}' \sim P\) are a pair of independent random variables and \(\textbf{y}\) is the vector of the actual values of all the time series. The energy score is a proper scoring rule for distributions defined on the entire hierarchy (Panagiotelis et al. 2023). We compute ES, with \(\alpha = 2\), using samples, as explained in Wickramasuriya (2023).

We use the skill score to compare the performance of a method with respect to a baseline method, in terms of percentage improvement. We use base as baseline method. For example, the skill score of NB on MASE is given by

$$\begin{aligned} \text {Skill}(\textit{NB}, \textit{base}) = \frac{\text {MASE}(\textit{base}) - \text {MASE}(\textit{NB})}{\left( \text {MASE}(\textit{base}) + \text {MASE}(\textit{NB})\right) / 2}. \end{aligned}$$

Note that the skill score is symmetric and scale-independent. For each level, we compute the skill score for each forecasting horizon, and take the average.

The skill scores for carparts are reported in Table 2. Both NB and samples methods yield a significant improvement for all the indicators, and for all the hierarchy levels. For both methods, the average improvement is about \(20\%\) for MASE, \(40\%\) for MIS and \(50\%\) for ES. The skill scores for syph are reported in Table 3. As before, the average improvement of NB and samples is significant for all indicators. For both datasets, the N method performs poorly, in many cases yielding negative skill scores. As observed in Corani et al. (2023), this method does not capture the asymmetry of the base forecasts. Finally, samples appears to perform better that NB. Indeed, the step of fitting a Negative Binomial distribution on the forecast samples may yield an additional source of error.

7 Conclusions

Our approach to probabilistic reconciliation based on conditioning allows to treat continuous and discrete forecast distributions in a unified framework. Moreover, the proposed BUIS is able to efficiently sample from continuous and discrete predictive distributions, provided in parametric form or as samples. We make available the BUIS algorithm within the R package bayesRecon (Azzimonti et al. 2023).

A future research direction is how to relax the assumption of conditional independence of the base forecasts. A second one is to study the implications of ignoring the behavior of the base forecast distribution outside the coherent subspace, which is a feature of reconciliation via conditioning and constitutes a major difference from reconciliation via projection.