Skip to main content
SpringerLink
Log in

Variations around a general quantum operator

  • Published:
The Ramanujan Journal Aims and scope Submit manuscript

Abstract

Let \(\,I\subseteq {\mathbb {R}}\,\) be an interval and \(\,\beta :\,I\rightarrow \,I\,\) a strictly increasing and continuous function with a unique fixed point \(\,s_0\in I\,\) that satisfies \(\,(s_0-t)(\beta (t)-t)\ge 0\,\) for all \(\,t\in I\), where the equality holds only when \(\,t=s_0\). For appropriate choices of the function \(\,\beta ,\) the quantum operator defined by Hamza et al., \(\,D_{\beta }[f](t):=\displaystyle \frac{f\big (\beta (t)\big )-f(t)}{\beta (t)-t}\,\) if \(\,t\ne s_0\,\) and \(\,D_{\beta }[f](s_0):=f^{\prime }(s_0)\,\) if \(\,t=s_0,\) generalizes both the Jackson \(\,q\)-operator \(\,D_{q}\,\) and the Hahn (quantum derivative) operator, \(\,D_{q,\omega }\). With respect to the inverse of this general quantum difference operator, the \(\,\beta \)-integral, we study properties of the corresponding Lebesgue spaces \(\,{\mathscr {L}}_{\beta }^p([a,b]).\)

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. In fact, \({\mathbb {K}}={\mathbb {X}}\) can represent any Banach space [24, p.2]

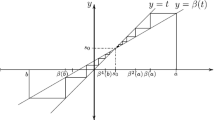
  2. This shows that, for every fixed \(\,x\in \,I\), the sequence \(\{\beta ^{k}(x)\}_k\,\) is strictly monotone decreasing or strictly monotone increasing according to \(\,x>s_0\,\) or \(\,x<s_0\), respectively. Proposition 1 shows that it converges in both cases to the fix point \(\,s_0\).

References

  1. Abreu, L.D.: A \(q\)-sampling theorem related to the \(q\)-Hankel transform. Proc. Am. Math. Soc. 133(4), 1197–1203 (2004)

    Article  MathSciNet  Google Scholar 

  2. Abreu, L.D.: Functions \(q\)-orthogonal with respect to their own zeros. Proc. Am. Math. Soc. 134(9), 2695–2701 (2006)

    Article  MathSciNet  Google Scholar 

  3. Abreu, L.D.: Real Paley–Wiener theorems for the Koornwinder–Swarttouw \(q\)-Hankel transform. J. Math. Anal. Appl. 334, 223–231 (2007)

    Article  MathSciNet  Google Scholar 

  4. Abreu, L.D., Bustoz, J., Cardoso, J.L.: The roots of the third Jackson \(q\)-Bessel function. Int. J. Math. Math. Sci. 2003(67), 4241–4248 (2003)

    Article  MathSciNet  Google Scholar 

  5. Abreu, L.D., Álvarez-Nodarse, R., Cardoso, J.L.: Uniform convergence of basic Fourier–Bessel series on a \(q\)-linear grid. Ramanujan J. 49, 421–449 (2019). https://doi.org/10.1007/s11139-018-0070-3

    Article  MathSciNet  MATH  Google Scholar 

  6. Abu-Risha, M.H., Annaby, M.H., Ismail, M.E.H., Mansour, Z.S.: Linear \(q\)-difference equations. Z. Anal. Anwend. 26, 481–494 (2007)

    Article  MathSciNet  Google Scholar 

  7. Aldwoah, K.A., Malinowska, A.B., Torres, D.F.M.: The power quantum calculus and variational problems. Dyn. Contin. Discrete Impuls. Syst. B 19(1–2), 93–116 (2012)

    MathSciNet  MATH  Google Scholar 

  8. Annaby, M.H.: \(q\)-Type sampling theorems. Results Math. 44, 214–225 (2003)

    Article  MathSciNet  Google Scholar 

  9. Annaby, M.H., Hassan, H.A.: Sampling theorems for Jackson–Nörlund transforms associated with Hahn–difference operators. J. Math. Anal. Appl. 464, 493–506 (2018)

    Article  MathSciNet  Google Scholar 

  10. Annaby, M.H., Mansour, Z.S.: Basic Sturm–Liouville problems. J. Phys. A 38, 3775–3797 (2005)

    Article  MathSciNet  Google Scholar 

  11. Annaby, M.H., Hamza, A.E., Aldwoah, K.A.: Hahn difference operator and associated Jackson–Nörlund integrals. J. Optim. Theory Appl. 154(1), 133–153 (2012)

    Article  MathSciNet  Google Scholar 

  12. Annaby, M.H., Hassan, H.A., Mansour, Z.S.: Sampling theorems associated with singular \(q\)-Sturm Liouville problems. Results Math. 62, 121–136 (2012)

    Article  MathSciNet  Google Scholar 

  13. Brito da Cruz, A.M.C., Martins, N., Torres, D.F.M.: Higher-order Hahn’s quantum variational calculus. Nonlinear Anal. 75(3), 1147–1157 (2012)

    Article  MathSciNet  Google Scholar 

  14. Bustoz, J., Cardoso, J.L.: Basic analog of Fourier series on a \(q\)-linear grid. J. Approx. Theory 112, 134–157 (2001)

    Article  MathSciNet  Google Scholar 

  15. Cardoso, J.L.: Basic Fourier series on a \(q\)-linear grid: convergence theorems. J. Math. Anal. Appl. 323, 313–330 (2006)

    Article  MathSciNet  Google Scholar 

  16. Cardoso, J.L.: Basic Fourier series: convergence on and outside the \(q\)-linear grid. J. Fourier Anal. Appl. 17(1), 96–114 (2011)

    Article  MathSciNet  Google Scholar 

  17. Cardoso, J.L.: A few properties of the third Jackson \(q\)-Bessel function. Anal. Math. 42(4), 323–337 (2016)

    Article  MathSciNet  Google Scholar 

  18. Cardoso, J.L.: On basic Fourier–Bessel expansions. SIGMA 14, 035 (2018)

    MathSciNet  MATH  Google Scholar 

  19. Cardoso, J.L., Petronilho, J.: Variations around Jackson’s quantum operator. Methods Appl. Anal. 22(4), 343–358 (2015)

    MathSciNet  MATH  Google Scholar 

  20. Cruz, A.M., Martins, N.: General quantum variational calculus. Stat. Optim. Inf. Comput. 6, 22–41 (2018)

    Article  MathSciNet  Google Scholar 

  21. Dhaouadi, L., Binous, W., Fitouhi, A.: Paley–Wiener theorem for the q-Bessel transform and associated \(q\)-sampling formula. Expos. Math. 27, 55–72 (2009)

    Article  MathSciNet  Google Scholar 

  22. Fitouhi, A., Dhaoudi, L.: On a \(q\)-Paley–Wiener theorem. J. Math. Anal. Appl. 294, 17–23 (2004)

    Article  MathSciNet  Google Scholar 

  23. Hamza, A.E., Shehata, E.M.: Some inequalities based on a general quantum difference operator. J. Inequal. Appl. 2015(38), 1–12 (2015)

    MathSciNet  MATH  Google Scholar 

  24. Hamza, A.E., Sarhan, A.M., Shehata, E.M., Aldwoah, K.A.: A general quantum difference calculus. Adv. Differ. Equ. 2015(182), 1–19 (2015)

    MathSciNet  MATH  Google Scholar 

  25. Hamza, A.E., Sarhan, A.M., Shehata, E.M.: Exponential, trigonometric and hyperbolic functions associated with a general quantum difference operator. Adv. Dyn. Syst. Appl. 12(1), 25–38 (2017)

    MathSciNet  Google Scholar 

  26. Hassan, H.A.: A completeness theorem for a Hahn–Fourier system and an associated classical sampling theorem. Results Math. 74, 34 (2019)

    Article  MathSciNet  Google Scholar 

  27. Ismail, M.E.H.: Classical and Quantum Orthogonal Polynomials in One Variable. With Two Chapters by Walter Van Assche. Encyclopedia of Mathematics and its Applications, vol. 98. Cambridge University Press, Cambridge (2005)

    MATH  Google Scholar 

  28. Ismail, M.E.H., Zayed, A.I.: A \(q\)-analogue of the Whittaker–Shannon–Kotel’nikov sampling theorem. Proc. Am. Math. Soc. 183, 3711–3719 (2003)

    Article  Google Scholar 

  29. Jackson, F.H.: On q-functions and a certain difference operator. Trans. R. Soc. Edinb. 46, 253–281 (1908)

    Article  Google Scholar 

  30. Jackson, F.H.: On \(q\)-definite integrals. Q. J. Pure Appl. Math. 41, 193–203 (1910)

    MATH  Google Scholar 

  31. Jackson, F.H.: Basic integration. Q. J. Math. 2, 1–16 (1951)

    Article  MathSciNet  Google Scholar 

  32. Jia, L., Cheng, J., Feng, Z.: A \(q\)-analogue of Kummers equation. Electron. J. Differ. Equ. 2017(31), 1–20 (2017)

    MathSciNet  Google Scholar 

  33. Koekoek, R., Lesky, P., Swarttouw, R.: Hypergeometric Orthogonal Polynomials and Their q-Analogues. With a Foreword by Tom H. Koornwinder. Springer, Berlin (2010)

    Book  Google Scholar 

  34. Koelink, E.: q-Special functions, basic hypergeometric series and operators. arXiv:1808.03441v1 [math.CA] (2018)

  35. Koornwinder, T.H.: Compact quantum groups and \(q\)-special functions. In: Representations of Lie Groups and Quantum Groups. Pitman Research Notes Mathematics Series, vol. 311, pp. 46–128. Longman Scientific and Technical, London (1994)

  36. Koornwinder, T.H., Swarttouw, R.F.: On \(q\)-analogues of the Fourier and Hankel transforms. Trans. Am. Math. Soc. 333, 445–461 (1992)

    MathSciNet  MATH  Google Scholar 

  37. Matsuo, A.: Jackson integrals of Jordan–Pochhammer type and quantum Knizhnik–Zamolodchikov equations. Commun. Math. Phys. 151, 263–273 (1993)

    Article  MathSciNet  Google Scholar 

  38. Petronilho, J.: Generic formulas for the values at the singular points of some special monic classical \(H_{q,\omega }\)-orthogonal polynomials. J. Comput. Appl. Math. 205(1), 314–324 (2007)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The author is grateful to J. Petronilho for the interesting discussions.

Author information

Authors and Affiliations

  1. Departamento de Matemática da ECT, UTAD, Quinta de Prados, 5001-801, Vila Real, Portugal

    J. L. Cardoso

Authors
  1. J. L. Cardoso
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to J. L. Cardoso.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This research was partially supported by Portuguese Funds through the FCT — Fundação para a Ciência e a Tecnologia—within the Project UID/MAT/00013/2013.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cardoso, J.L. Variations around a general quantum operator. Ramanujan J 54, 555–569 (2021). https://doi.org/10.1007/s11139-019-00210-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11139-019-00210-8

Keywords

Mathematics Subject Classification

Search

Navigation