Non-Hermitian quantum annealing in the antiferromagnetic Ising chain

Abstract

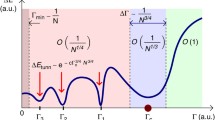
A non-Hermitian quantum optimization algorithm is created and used to find the ground state of an antiferromagnetic Ising chain. We demonstrate analytically and numerically (for up to $N=1,024$ spins) that our approach leads to a significant reduction in the annealing time that is proportional to $\ln N$, which is much less than the time (proportional to $N^2$) required for the quantum annealing based on the corresponding Hermitian algorithm. We propose to use this approach to achieve similar speed-up for NP-complete problems by using classical computers in combination with quantum algorithms.

Appendices

Appendix A: One-dimensional antiferromagnetic Ising chain in a transverse field

We consider the 1-dimensional antiferromagnetic Ising chain in a transverse magnetic field governed by the following non-Hermitian Hamiltonian:

$$\begin{aligned} H= \frac{J}{2}\sum ^N_{n=1}\big (g \sigma ^x_n + \sigma ^z_n \sigma ^z_{n+1} - i{\delta }\big ( {1\!\!1}-\sigma ^{x}_n \big )\big ), \end{aligned}$$

(56)

with the periodic boundary condition, ${\varvec{\sigma }}_{N+1} ={\varvec{\sigma }}_1$. The external magnetic field is associated with the parameter, $g$, the spontaneous decay is described by the parameter, $\delta$.

The non-Hamiltonian in Eq. (56) can be diagonalized using the standard Jordan-Wigner transformation, following well-known procedures described in [16–20] for Hermitian Hamiltonians. Note that, the diagonalization of the non-Hermitian Hamiltonians requires one to deal with some additional mathematical obstacles. For instance, in the non-Hermitian case the right and the left eigenvectors are different, and generally one has a complex energy spectrum.

The Jordan-Wigner transformation, which is mapping of a spin-1/2 system to a system of spinless fermions, is given by

$$\begin{aligned} \sigma ^x_n&= 1-2 c^\dagger _n c_n, \end{aligned}$$

(57)

$$\begin{aligned} \sigma ^y_n&= i\left( c^\dagger _n - c_n\right) \prod _{m<n}\left( 1-2 c^\dagger _m c_m\right) , \end{aligned}$$

(58)

$$\begin{aligned} \sigma ^z_n&= -\left( c_n + c^\dagger _n\right) \prod _{m<n}\left( 1-2 c^\dagger _m c_m\right) , \end{aligned}$$

(59)

in which the $c_n$ are fermionic operators that satisfy anticommutation relations: $\{c^\dagger _m,c_n\} = \delta _{mn}$ and $\{c_m,c_n\}=\{c^\dagger _m,c^\dagger _n\}=0$. Applying these transformations, we obtain

$$\begin{aligned} H =\frac{J}{2}\sum ^N_{n=1}\big (c^\dagger _n c_{n+1 }+ c^\dagger _{n+1}c_{n}+ c_{n +1}c_{n }+ c^\dagger _{n} c^\dagger _{n+1}+ g(1-2 c^\dagger _n c_{n }) - 2i\delta c^\dagger _n c_{n } \big ).\nonumber \\ \end{aligned}$$

(60)

The periodic boundary condition imposed on the spin operators leads to the following boundary condition for the fermionic operators:

$$\begin{aligned} c_{N+1} = - \hbox {e}^{i\pi {{\fancyscript{N}}}_F} c_1, \end{aligned}$$

(61)

${{\fancyscript{N}}}_F = \sum ^N_{n=1} c^\dagger _{n} c^\dagger _{n}$ being the total number of fermions. From Eq. (57) it follows that ${{\fancyscript{N}}}_F= N/2- S^x$, where $S^x$ is the total $x$-component of the spins. For the particular choice of parameters, $g=\delta =0$, we obtain, $S^x =0$ and ${{\fancyscript{N}}}_F= N/2$. Thus, for $S^x =0$ and ${{\fancyscript{N}}}_F= N/2$ we obtain periodic (antiperiodic) boundary conditions if $N/2$ is odd (even). Note that since the parity of the fermions is conserved, the imposed boundary conditions are valid for all values of the parameters, $g$ and $\delta$.

Next, by applying the Fourier transformations,

$$\begin{aligned} c_n = \frac{\hbox {e}^{-i\pi /4}}{\sqrt{N}}\sum _k c_k \hbox {e}^{i2\pi kn/N}, \end{aligned}$$

(62)

we find that the Hamiltonian (60) can be recast in Fourier space as follows:

$$\begin{aligned} H= -\frac{J}{2}\sum _{k}\Big (2({\tilde{g}} - \cos \varphi _k)c^\dagger _k c_k- g + \sin \varphi _k(c^\dagger _k c^\dagger _{-k} + c_{-k} c_{k} ) \Big ), \end{aligned}$$

(63)

where ${\tilde{g}} = g+i\delta$ and $\varphi _k = {2\pi k}/{N}$. For periodic boundary conditions, $c_{N+1}=c_1$, the wave number, $k$, takes the following discrete values:

$$\begin{aligned} k=-\frac{N}{2}, \ldots , 0,1, \ldots , \frac{N}{2}-1, \end{aligned}$$

(64)

and for antiperiodic boundary conditions, $c_{N+1}=-c_1$, we obtain

$$\begin{aligned} k=\pm \frac{1}{2},\pm \frac{3}{2},\ldots , \pm \frac{N-1}{2}, \end{aligned}$$

(65)

In what follows, we impose the antiperiodic boundary conditions for the fermionic operators.

The Hamiltonian, $H$, can be diagonalized using the generalized Bogoliubov transformation [14, 21]. Its spectrum is given by $\varepsilon _{\pm }(k)= \varepsilon _{0} \pm \varepsilon _k$, in which $\varepsilon _{0} = J\cos \varphi _k- iJ\delta$, and $\varepsilon _k = J\sqrt{{\tilde{g}}^2 - 2{\tilde{g}}\cos \varphi _k +1}$. There are two (right) eigenstates for each $k$,

$$\begin{aligned} |u_{+}(k)\rangle&= \left( \begin{array}{c} \cos \frac{\theta _k}{2} \\ \sin \frac{\theta _k}{2} \end{array}\right) , \end{aligned}$$

(66)

$$\begin{aligned} |u_{-}(k)\rangle&= \left( \begin{array}{c} -\sin \frac{\theta _k}{2}\\ \cos \frac{\theta _k}{2} \end{array}\right) , \end{aligned}$$

(67)

in which

$$\begin{aligned} \cos \theta _k&= \frac{ \cos \varphi _k - {\tilde{g}}}{\sqrt{{\tilde{g}}^2 - 2{\tilde{g}}\cos \varphi _k +1}}, \end{aligned}$$

(68)

$$\begin{aligned} \sin \theta _k&= - \frac{ \sin \varphi _k}{\sqrt{{\tilde{g}}^2 - 2{\tilde{g}}\cos \varphi _k +1}}, \end{aligned}$$

(69)

with $\theta _k$ being a complex angle.

Since for each $k$, the ground state lies into the two-dimensional Hilbert space spanned by $|0\rangle _k |0\rangle _{-k}$ and $|1\rangle _k |1\rangle _{-k}$, it is sufficient to project $H$ onto this subspace. For a given value of $k$, both of these states can be represented as a point on the complex two-dimensional sphere, $S^2_c$. In this subspace, the Hamiltonian, $H_k$, takes the form

$$\begin{aligned} {H}_k = {\varepsilon _0} {1}- {J} \left( \begin{array}{c@{\quad }c} {\tilde{g}}- \cos \varphi _k &{} \sin \varphi _k \\ \sin \varphi _k &{} -{\tilde{g}}+ \cos \varphi _k \\ \end{array} \right) . \end{aligned}$$

(70)

Its ground state can be written as a product of qubit-like states, $|\psi _g\rangle = \bigotimes _{k}|u_{-}(k)\rangle$, so that:

$$\begin{aligned} |\psi _g\rangle = \bigotimes _{k} \Big (\cos \frac{\theta _k}{2}|0\rangle _k |0\rangle _{-k} -\sin \frac{\theta _k}{2}|1\rangle _k |1\rangle _{-k} \Big ), \end{aligned}$$

(71)

where, $|0\rangle _k$, is the vacuum state of the mode $c_k$, and $|1\rangle _k$ is the excited state: $|1\rangle _k =c^\dagger _k |0\rangle _k$.

For $|{\tilde{g}}|\gg 1$, the ground state is paramagnetic with all spins oriented along the $x$ axis. From Eq. (68), we obtain $\cos \theta _k \rightarrow - 1$ as $|{\tilde{g}}| \rightarrow \infty$. From here, it follows that, $|u_{-}(k)\rangle \rightarrow \left( \begin{array}{c} 1 \\ 0 \\ \end{array} \right)$. Thus, the north pole of the complex Bloch sphere corresponds to the paramagnetic ground state. On the other hand, when $|g|\ll 1$ there are two degenerate antiferromagnetic ground states with neighboring spins polarized in opposite directions along the $z$-axis. The real part of the complex energy reaches its minimum at the point defined by $\cos \theta _k = 1$, and hence, the south pole of the complex sphere is related to the pure antiferromagnetic ground state.

Appendix B: Exact solution of the non-Hermitian Landau-Zener problem

The non-Hermitian Hamiltonian, ${\fancyscript{H}}(t)$, projected on the two-dimensional subspace spanned by $|k_1\rangle = { \left( \begin{array}{c} 1 \\ 0 \\ \end{array} \right) }$ and $|k_0\rangle ={ \left( \begin{array}{c} 0 \\ 1 \\ \end{array} \right) }$, takes the form

$$\begin{aligned} {\fancyscript{H}}_k(t) = \varepsilon _0(t) {1\!\!1} -J \left( \begin{array}{c@{\quad }c} {\tilde{g}}(t)- \cos \varphi _k &{} \sin \varphi _k \\ \sin \varphi _k &{} -{\tilde{g}}(t)+ \cos \varphi _k \\ \end{array} \right) , \end{aligned}$$

(72)

where $\varepsilon _0(t)= J\cos \varphi _k-iJ\delta (t)$ and ${\tilde{g}}(t) = g(t) + i\delta (t)$. We assume a linear dependence of the function, ${\tilde{g}}(t)$, on time:

$$\begin{aligned} {\tilde{g}}(t) = \left\{ \begin{array}{l} \gamma (\tau -t), \quad 0 \le t \le \tau \\ 0, \quad t > \tau \end{array} \right. , \end{aligned}$$

(73)

where, $\gamma =(g+i\delta )/\tau$, and $g,\,\delta$ are real parameters.

The general wave functions, $|\psi _k\rangle$ and $\langle \tilde{\psi }_k |$, satisfy the Schrödinger equation and its adjoint equation

$$\begin{aligned} i\frac{\partial }{\partial t}|\psi _k\rangle&= {\fancyscript{H}}_k(t)|\psi _k\rangle , \end{aligned}$$

(74)

$$\begin{aligned} -i\frac{\partial }{\partial t}\langle \tilde{\psi }_k |&= \langle \tilde{\psi }_k |{\fancyscript{H}}_k(t). \end{aligned}$$

(75)

Presenting $|\psi _k(t)\rangle$ as a linear superposition

$$\begin{aligned} |\psi _k(t)\rangle = (u_k(t)|k_0\rangle + v_k(t)|k_1\rangle ) \hbox {e}^{-i\int \varepsilon _0(t)\hbox {d}t}, \end{aligned}$$

(76)

and inserting (76) into Eq. (74), we obtain

$$\begin{aligned} i\dot{u}_k&= J\big (({\tilde{g}} - \cos \varphi _k)\,u_k - \sin \varphi _k\, v_k\big ), \end{aligned}$$

(77)

$$\begin{aligned} i\dot{v}_k&= -J\big (\sin \varphi _k\, u_k +({\tilde{g}} - \cos \varphi _k)\,v_k \big ). \end{aligned}$$

(78)

Let $z_k(t) = \hbox {e}^{i\pi /4}\sqrt{2J/\gamma }\big (\gamma (\tau -t)-\cos \varphi _k\big )$ be a new variable. Then, for new functions, $u_k(t)= U_k(z_k)$ and $v_k(t) = V_k(z_k)$, we obtain

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}z_k}U_k&= \frac{z_k}{2}U_k -\sqrt{i\nu _k}V_k, \end{aligned}$$

(79)

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}z_k}V_k&= -\frac{z_k}{2}V_k -\sqrt{i\nu _k}U_k, \end{aligned}$$

(80)

where $\nu _k= (J/2\gamma )\sin ^2 \varphi _k$, and the complex ‘time’ $z_k$ runs from $z_k(0) = \hbox {e}^{i\pi /4}\sqrt{2J/\gamma }\big (\gamma \tau -\cos \varphi _k\big )$ to $z_k(\tau ) = -\hbox {e}^{i\pi /4}\sqrt{2J/\gamma }\cos \varphi _k$.

From Eqs. (79), (80), we obtain the second order Weber equations

$$\begin{aligned} \frac{\hbox {d}^2}{\hbox {d}z^2_k}U_k - \Big ( \frac{1}{2} + \frac{z_k^2}{4}+i\nu _k\Big )U_k&= 0, \end{aligned}$$

(81)

$$\begin{aligned} \frac{\hbox {d}^2}{\hbox {d}z^2_k}V_k + \Big (\frac{1}{2} -\frac{z_k^2}{4} -i\nu _k\Big )V_k&= 0. \end{aligned}$$

(82)

Solution of the Weber’s equations is given by the parabolic cylinder functions, $D_{-i\nu _k}(\pm z)$ and $D_{i\nu _k-1}(\pm i z)$.

We obtain the solutions of Eqs. (79), (80) in the form

$$\begin{aligned} U_{k}(z_k)&= B_k D_{i\nu _k}(iz_k) +{\sqrt{i\nu _k }} A_k D_{-i\nu _k-1}(z_k), \end{aligned}$$

(83)

$$\begin{aligned} V_{k}(z_k)&= A_k D_{-i\nu _k}(z_k) -i\sqrt{i\nu _k } B_k D_{i\nu _k-1}(iz_k)), \end{aligned}$$

(84)

where the constants, $A_k$ and $B_k$, are determined from the initial conditions.