On Baskakov–Szász–Mirakyan-type operators preserving exponential type functions

Abstract

The current article deals with the study of Baskakov–Szász–Mirakyan operators which reproduces constant and exponential functions. We discuss a uniform estimate and establish a quantitative result for the modified operators.

1 Baskakov–Szász–Mirakyan operators

In [7] was introduced the Baskakov–Szász–Mirakyan operators as follows:

$$\begin{aligned} B_n(f;x)=\displaystyle n\sum _{k=1}^{\infty } b_{n,k}(x)\int _0^{\infty } s_{n,k-1}(t)f(t)dt+b_{n,0}(x)f(0), \end{aligned}$$

(1)

where

$$\begin{aligned} \displaystyle b_{n,k}(x) = \frac{(n)_k}{k!} \frac{x^k}{(1+x)^{n+k}},\quad \displaystyle s_{n,k}(t) = e^{-nt} \frac{(nt)^{k}}{(k)!}, \end{aligned}$$

and $(n)_0=1$, $(n)_k=n(n+1)\cdots (n+k-1)$ for $k\ge 1$. Some approximation properties of these operators and their different versions have been discussed in [9, 10]. Recently, Acar et al. [1] introduced a modified form of the Szász–Mirakyan operator that reproduces the functions 1 and $e^{2ax}, a>0$ fixed. This study was continued by Gupta and Aral [11], where they discussed a Kantorovich type modification of Szász–Mirakyan operators, preserving $e^{-x}$ and constant functions. A modification of the Phillips operators, which reproduces the exponential function along with constant function, was also studied in [12]. So, using the technique proposed in [1, 11, 12], we modify the operators defined in (1) as follows:

$$\begin{aligned} G_{n}(f,x)= & {} n \sum \limits _{k=1}^{\infty } \frac{(n)_k}{k!}(1+a_n(x))^{-n} \left( \frac{b_n(x)}{1+b_n(x)}\right) ^k \nonumber \\&\int \limits _{0}^{\infty } s_{n,k-1}(t) \ f(t) \ dt+(1+a_n(x))^{-n}f(0), \end{aligned}$$

(2)

In case $a_n(x)=b_n(x)=x$, we get the operators due to Agrawal and Mohammad [7]. Suppose that operators (2) reproduce $e^{ax}$ and $e^{bx}$. After simple computation, we get

$$\begin{aligned} n \int \limits _{0}^{\infty } e^{-nt} \frac{(nt)^{k-1}}{(k-1)!} \ e^{At} \ dt= & {} \left( \frac{n}{n-A} \right) ^{k}, \quad \text {for } \, n>A. \end{aligned}$$

(3)

Thus, using (3) and the well known binomial series $\sum _{k=0}^{\infty } \frac{(a)_k}{k!}z^k=(1-z)^{-a},|z|<1,$ we have

$$\begin{aligned} G_{n}(e^{at},x) =e^{ax}&= \frac{1}{(1+a_n(x))^n } \sum \limits _{k=0}^{\infty } \frac{(n)_k}{k!} \left[ \frac{nb_n(x)}{(n-a)(1+b_n(x))} \right] ^k \nonumber \\&= \frac{1}{(1+a_n(x))^n } \left[ 1-\frac{nb_n(x)}{(n-a)(1+b_n(x))} \right] ^{-n}\nonumber \\&= \left[ \frac{1+b_n(x)}{1+a_n(x)}\right] ^n \left[ \frac{(n-a)}{n-a(1+b_n(x))}\right] ^{n}. \end{aligned}$$

Similarly

$$\begin{aligned} G_{n}(e^{bt},x) =e^{bx}&= \left[ \frac{1+b_n(x)}{1+a_n(x)}\right] ^n\left[ \frac{(n-b)}{n-b(1+b_n(x))}\right] ^{n}. \end{aligned}$$

These imply

$$\begin{aligned} b_n(x)=\frac{(n^2-na-nb+ab)(e^{(a-b)x/n}-1)}{a(n-b)e^{(a-b)x/n}-b(n-a)} \end{aligned}$$

(4)

and

$$\begin{aligned} a_n(x)=\displaystyle \frac{(n-b)e^{-bx/n}-(n-a)e^{-ax/n}-(a-b)}{a-b}. \end{aligned}$$

(5)

Our study is given for $a=0, b=-1$ and $a=0, b=-2$. In these two cases our operator (2) is positive and preserves the exponential functions $e^{ax}$ and $e^{bx}$, respectively.

2 Lemmas

Lemma 1

For $\theta \in \mathbb {R}$, we have

$$\begin{aligned} G_{n}(e^{\theta t},x)=&\left[ \frac{1+b_n(x)}{1+a_n(x)}\right] ^n\left[ \frac{n-\theta }{n-\theta (1+b_n(x))}\right] ^{n}\\ =&\left[ \displaystyle \frac{e^{(a-b)x/n}n(n-b)-n(n-a)}{a(n-b)e^{(a-b)x/n}-b(n-a)}\times \frac{a-b}{(n-b)e^{-bx/n}-(n-a)e^{-ax/n}} \right] ^n \\&\times \left[ \displaystyle \frac{(n-\theta )}{n-\theta \left( \displaystyle \frac{e^{(a-b)x/n}n(n-b)-n(n-a)}{a(n-b)e^{(a-b)x/n}-b(n-a)}\right) }\right] ^{n}, \end{aligned}$$

where $a_n(x)$ and $b_n(x)$ are used from (4) to (5).

Lemma 2

For $\mu ^G_{n,r}(x)=G_n(t^r,x)$ moments may be obtained as

• (i) $\mu ^G_{n,0}(x) =1$,

• (ii) $\mu ^G_{n,1}(x) = b_n(x)$,

• (iii) $\mu ^G_{n,2}(x)= \displaystyle \frac{1}{n} b_n(x)(b_n(x)n+b_n(x)+2)$,

• (iv) $\mu ^G_{n,3}(x) =\displaystyle \frac{1}{n^2}b_n(x) \left\{ b_n^2(x)n^2+3b_n^2(x)n+2b_n^2(x)+6b_n(x)n+6b_n(x)+6\right\}$,

• (v) $\mu ^G_{n,4}(x) =\displaystyle \frac{1}{n^3}b_n(x)\left\{ b_n^3(x)n^3+6b_n^3(x)n^2+11b_n^3(x)n+12b_n^2(x)n^2+6b_n^3(x)\right. \left. \qquad \qquad \qquad +\,36b_n^2(x)n +24b_n^2(x)+36b_n(x)n+36b_n(x)+24\right\} .$

Lemma 3

Let $T^G_{n,r}(x):=G_n((t-x)^r,x)$ be the central moments of the operators (2). Then, we have

• (i) $T^G_{n,0}(x) = 1$,

• (ii) $T^G_{n,1}(x) =(b_n(x)-x)$,

• (iii) $T^G_{n,2}(x)= \displaystyle \frac{1}{n}\left\{ b_n^2(x)n-2b_n(x)nx+nx^2+b_n^2(x)+2b_n(x)\right\}$.

Also, it follows

$$\begin{aligned}&\lim _{n\rightarrow \infty }nT_{n,1}^G(x)=\displaystyle -\frac{1}{2}x^2a-\frac{1}{2}x^2b-ax-bx, \\&\lim _{n\rightarrow \infty }nT_{n,2}^G(x)=x^2+2x. \end{aligned}$$

3 Main results

We consider by $C^*[0,\infty )$ the class of real-valued continuous functions f(x), possessing finite limit for x sufficiently large and equipped with the uniform norm. Uniform convergence of certain sequence of positive linear operators was considered in [8]. About four decades later Holhoş [13] considered this problem and obtained the following quantitative estimate for a sequence $L_n,$ of positive linear operators:

Denote $\varphi _i(x)=e^{-ix}$, $x\in [0,\infty )$, $i=0,1,2$.

Theorem A

[13] For a sequence of positive linear operators $L_n: C^*[0,\infty )\rightarrow C^*[0,\infty )$, if for $i=0,1,2$ we denote the norms $|| L_n(e^{-it})-\varphi _i||_{[0,\infty )}$ as $\alpha _n, \beta _n$ and $\gamma _n$ respectively, and $\alpha _n,\beta _n,\gamma _n$ tend to 0 as $n\rightarrow \infty$, then

$$\begin{aligned} || L_nf-f||_{[0,\infty )}\le \alpha _n ||f||_{[0,\infty )}+(2+\alpha _n)\omega ^*(f,\sqrt{\alpha _n+2\beta _n+\gamma _n}), \end{aligned}$$

where the modulus of continuity is given by

$$\begin{aligned} \omega ^*(f,\delta ):= \mathop {\mathop {\sup }\limits _{|e^{-x}-e^{-t}|\le \delta }}\limits _{x,t>0} |f(t)-f(x)|. \end{aligned}$$

Theorem 1

For $f\in C^*[0,\infty ),$ we have

• (i) If $a=0, b=-1$, then

  $$\begin{aligned} || G_nf-f||_{[0,\infty )}\le 2\omega ^*\left( f,\sqrt{\gamma _n}\right) , \end{aligned}$$

  (6)

  where

  $$\begin{aligned} \gamma _n= & {} || G_n(e^{-2t})-\varphi _2||_{[0,\infty )} \rightarrow 0, n\rightarrow \infty . \end{aligned}$$

• (ii) If $a=0, b=-2$, then

  $$\begin{aligned} || G_nf-f||_{[0,\infty )}\le 2\omega ^*\left( f,\sqrt{2\beta _n}\right) , \end{aligned}$$

  (7)

  where

  $$\begin{aligned} \beta _n= & {} || G_n(e^{-t})-\varphi _1||_{[0,\infty )} \rightarrow 0, n\rightarrow \infty . \end{aligned}$$

Proof

(i) For $a=0, b=-1$, by Lemma 1, the operators $G_n$ satisfy

$$\begin{aligned} G_{n}\left( e^{\theta t},x\right)&= \left[ \frac{n-\theta }{n-\theta \left[ e^{x/n}(n+1)-n\right] }\right] ^{n} \end{aligned}$$

which preserve $e^{-x}$ and constants, so $\alpha _n=\beta _n=0$. We only have to evaluate $\gamma _n$. By simple calculations we obtain:

$$\begin{aligned} G_n\left( e^{-2t},x\right) =\left[ 1+\frac{2(n+1)\left( e^{\frac{x}{n}}-1\right) }{n+2}\right] ^{-n}. \end{aligned}$$

Using the software Maple, we get

$$\begin{aligned} G_n(e^{-2t};x)=e^{-2x}+\displaystyle \frac{e^{-2x}\left( x^2+2x\right) }{n}+\frac{e^{-2x}x}{2n^2}\left( x^3+2x^2-2x-8\right) +{\mathcal O}\left( n^{-3}\right) . \end{aligned}$$

Since,

$$\begin{aligned} \displaystyle \sup _{x\in [0,\infty )}e^{-2x}= & {} 1,\quad \displaystyle \sup _{x\in [0,\infty )}xe^{-2x}=\frac{e^{-1}}{2},\quad \displaystyle \sup _{x\in [0,\infty )}x^2e^{-2x}=e^{-2}, \\ \displaystyle \sup _{x\in [0,\infty )}x^3e^{-2x}= & {} \frac{27}{8}e^{-3},\quad \displaystyle \sup _{x\in [0,\infty )}x^4e^{-2x}=16e^{-4}, \end{aligned}$$

we obtain

$$\begin{aligned} \gamma _n&=\Vert G_n\left( e^{-2t}\right) -\varphi _2 \Vert _{[0,\infty )}=\displaystyle \sup _{x\in [0,\infty )}|G_n\left( e^{-2t};x\right) -e^{-2x}|\\&\le \displaystyle \frac{1}{n}\left( e^{-2}+e^{-1} \right) +\frac{1}{n^2}\left( 8e^{-4}+\frac{27}{8}e^{-3}+e^{-2}+2e^{-1} \right) +{\mathcal O}\left( n^{-3}\right) \le {\mathcal O}\left( n^{-1}\right) . \end{aligned}$$

Using Theorem A, the proof of (i) is completed.

(ii) For $a=0, b=-2$, by Lemma 1, the operators $G_n$ satisfy

$$\begin{aligned} G_{n}\left( e^{\theta t},x\right)&= \left[ \frac{2(n-\theta )}{2n-\theta \left[ e^{2x/n}(n+2)-n\right] }\right] ^{n} \end{aligned}$$

which preserve $e^{-2x}$ along with constant functions, so $\alpha _n=\gamma _n=0$. We only have to evaluate $\beta _n$.

By simple calculations we obtain:

$$\begin{aligned} G_n(e^{-t},x)=\left[ 1+\frac{(n+2)\left( e^{\frac{2x}{n}}-1\right) }{2(n+1)}\right] ^{-n}. \end{aligned}$$

Making use of the software Maple, we immediately have

$$\begin{aligned} G_n\left( e^{-t};x\right)= & {} e^{-x}+\frac{e^{-x}}{n} \left( -\frac{1}{2}x^2-x\right) \\&+ \,\frac{e^{-x}}{n^2} \left( \frac{1}{2}x^3+\frac{1}{2} x^2+x+\frac{1}{8}x^4\right) +{\mathcal O}(n^{-3}). \end{aligned}$$

Using the identities

$$\begin{aligned} \displaystyle \sup _{x\in [0,\infty )}e^{-x}= & {} 1,\quad \displaystyle \sup _{x\in [0,\infty )}xe^{-x}=e^{-1},\quad \displaystyle \sup _{x\in [0,\infty )}x^2e^{-x}=4e^{-2}, \\ \displaystyle \sup _{x\in [0,\infty )}x^3e^{-x}= & {} 27e^{-3},\quad \displaystyle \sup _{x\in [0,\infty )}x^4e^{-x}=2566e^{-4},\quad \displaystyle \sup _{x\in [0,\infty )}x^5e^{-x}=3125e^{-5} \end{aligned}$$

we have

$$\begin{aligned} \beta _n&=\Vert G_n(e^{-t})-\varphi _1 \Vert _{[0,\infty )}=\displaystyle \sup _{x\in [0,\infty )}|G_n(e^{-t};x)-e^{-x}|\\&\le \frac{1}{n}\left( 2e^{-2}+e^{-1}\right) + \frac{1}{n^2}\left( \frac{27}{2}e^{-3}+2e^{-2}+e^{-1}+32e^{-4}\right) \\&\quad +\,{\mathcal O}(n^{-3})\le {\mathcal O}(n^{-1}). \end{aligned}$$

Using Theorem A, the proof of (ii) is completed. $\square$

Example 1

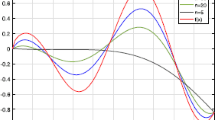
Let $a=0,b=-1$. The convergence behaviour of the operators $G_n(f,x)$ is illustrated in Fig. 1, where $f(x)=x^3e^{-3x}$, $x\in [0,7]$ and $n\in \{10,20,30\}$. We can see that for the values of n increasing, the graph of the operator $G_n(f,x)$ goes to the graph of the function f.

Fig. 1

The error of $G_n(f,x)$ to f(x)

Example 2

Let $a=0, b=-2$. The convergence behaviour of $G_n(f,x)$ is illustrated in the Fig. 2, where $f(x)=2x^4-3x^2+6$, $x\in [0,2]$ and $n\in \{50,100,500\}$. We can see that for the values of n increasing, the graph of $G_n(f,x)$ goes to the graph of the function f.

Fig. 2

The error of $G_n(f,x)$ to f(x)

Lemma 4

The Szász–Mirakyan–Kantorovich operators defined in (1) verify the identities:

• (i) $B_n(e^{-t},x)=\left( \displaystyle \frac{n+x+1}{n+1} \right) ^{-n} =e^{-x}+\displaystyle \frac{e^{-x}}{n}\left( \frac{x^2}{2}+x\right) +{\mathcal O}\left( \frac{1}{n^2}\right)$,

• (ii) $B_n(e^{-2t},x)=\left( \displaystyle \frac{n+2x+2}{n+2} \right) ^{-n}=e^{-2x}+\displaystyle \frac{e^{-2x}}{n}(2x^2+4x)+{\mathcal O}\left( \frac{1}{n^2}\right)$.

Remark 1

For $f\in C^*[0,\infty )$,the original Baskakov–Szász–Mirakyan operators verify:

$$\begin{aligned} \Vert B_nf-f \Vert _{[0,\infty )}\le 2\omega ^*\left( f,\sqrt{2\tilde{\beta }_n+\tilde{\gamma }_n} \right) , \end{aligned}$$

(8)

where

$$\begin{aligned} \tilde{\beta }_n&=\displaystyle \sup _{x\in [0,\infty )}\left| B_n\left( e^{-t}\right) -e^{-x}\right| \le \displaystyle \frac{1}{n}\left( 2e^{-2}+e^{-1}\right) +{\mathcal O}\left( \frac{1}{n^2}\right) \le {\mathcal O}\left( n^{-1}\right) ,\\ \tilde{\gamma }_n&=\displaystyle \sup _{x\in [0,\infty )}\left| B_n\left( e^{-2t}\right) -e^{-2x}\right| \le \displaystyle \frac{2}{n}\left( e^{-2}+e^{-1}\right) +{\mathcal O}\left( \frac{1}{n^2}\right) \le {\mathcal O}\left( n^{-1}\right) . \end{aligned}$$

Since $\gamma _n\le \tilde{\gamma }_n$ and $\beta _n\le \tilde{\beta }_n$, from the relations (6), (7), (8) it follows the better approximation for the modified Baskakov–Szász–Mirakyan operators $G_n$ than the usual Baskakov–Szász–Mirakyan operators $B_n$.

Example 3

Let $f(x)=-2x^2e^{-3x}$, $n=20$, $x\in [0,5]$. For $a=0,b=-1$, respectively $a=0,b=-2$, the approximation to the function f by the modified operator $G_{n}$, and the classical ones is illustrated in the Fig. 3. We note that in this case the modified operators $G_{n}$ presents an order of approximation better than the operator $B_n$. In Table 1 we have computed the error of approximation for these operators at some points.

Fig. 3

The convergence of $G_{n}$, $B_n$ to f

Table 1 Error of approximation for $G_n$ and $B_n$

In the next result, we present a quantitative form of Voronovskaya formula. Nowadays such a result has been studied for many operators and for many moduli of continuity in classical and weighted cases (see [2,3,4,5,6, 14]).

Theorem 2

Let $f,f^{\prime \prime }\in C^*[0,\infty )$, then for any $x\in [0,\infty )$, we have

$$\begin{aligned}&\left| n[G_n(f,x)-f(x)]+\left( ax+bx+\frac{ax^2}{2}+\frac{bx^2}{2}\right) f^\prime (x)-\left( x+\displaystyle \frac{x^2}{2}\right) f^{\prime \prime }(x)\right| \\&\quad \le \left| p_n(x)\right| \cdot \left| f^{\prime }(x)\right| +\left| q_n(x)\right| \cdot \left| f^{\prime \prime }(x)\right| \\&\qquad +\,2 \left[ 2q_n(x)+\left( x^2+2x\right) +r_n(x)\right] \omega ^*\left( f^{\prime \prime },n^{-1/2}\right) , \end{aligned}$$

where

$$\begin{aligned} p_n(x)&=nT^G_{n,1}(x)+\left( ax+bx+\frac{ax^2}{2}+\frac{bx^2}{2}\right) \\ q_n(x)&= \frac{1}{2}\left[ nT^G_{n,2}(x)-(x^2+2x)\right] \\ r_n(x)&=n^2\left[ G_n\left( \left( e^{-x}-e^{-t}\right) ^4,x\right) \cdot T^G_{n,4}(x)\right] ^{1/2}. \end{aligned}$$

Proof

By Taylor’s expansion, we have

$$\begin{aligned} f(t)= \sum _{i=0}^2\frac{f^{(i)}(x)}{i!}(t-x)^i+h(t,x)(t-x)^2, \end{aligned}$$

(9)

where

$$\begin{aligned} h(t,x)=\frac{f^{\prime \prime }(\eta )-f^{\prime \prime }(x)}{2} \end{aligned}$$

and $\eta$ is a number lying between x and t. If we apply the operator $G_n$ to both sides of (9), we have

$$\begin{aligned} \left| G_n(f,x)-f(x)-T^G_{n,1}(x)f^\prime (x)-\frac{1}{2}T^G_{n,2}(x) f^{\prime \prime }(x)\right|\le & {} \left| G_n\left( h(t,x)(t-x)^2,x\right) \right| . \end{aligned}$$

Applying Lemma 3, we get

$$\begin{aligned}&\left| n[G_n(f,x)-f(x)]+\left( ax+bx+\frac{ax^2}{2}+\frac{bx^2}{2}\right) f^\prime (x)-\left( x+\frac{x^2}{2}\right) f^{\prime \prime }(x)\right| \\&\quad \le \left| nT^G_{n,1}(x)+\left( ax+bx+\frac{ax^2}{2}+\frac{bx^2}{2}\right) \right| \left| f^\prime (x)\right| \\&\qquad +\,\frac{1}{2}\left| nT^G_{n,2}(x)-(x^2+2x)\right| \left| f^{\prime \prime }(x)\right| \\&\qquad +\,\left| nG_n(h(t,x)(t-x)^2,x)\right| \\&\quad \le \left| p_n(x)\right| \cdot \left| f^{\prime }(x)\right| +\left| q_n(x)\right| \cdot \left| f^{\prime \prime }(x)\right| +\left| nG_n\left( h(t,x)(t-x)^2,x\right) \right| . \end{aligned}$$

To complete the proof of the theorem, it remains to estimate the term $|nG_n(h(t,x)(t-x)^2,x)|$. Applying the methods used in [1], we can write

$$\begin{aligned} |h(t,x)|\le 2\left( 1+\frac{(e^{-x}-e^{-t})^2}{\delta ^2}\right) \omega ^*\left( f^{\prime \prime },\delta \right) ,\quad \delta >0 \end{aligned}$$

Obviously using this and Cauchy–Schwarz inequality and choosing $\delta =n^{-1/2}$, we get

$$\begin{aligned} nG_n(|h(t,x)|(t-x)^2,x)\le & {} 2n\omega ^*(f^{\prime \prime },\delta )\cdot T^G_{n,2}(x)\\&+\,\frac{2n}{\delta ^2}|\omega ^*(f^{\prime \prime },\delta ) \left[ G_n\left( (e^{-x}-e^{-t})^4,x\right) \right] ^{1/2} \\&\times \left[ T^G_{n,4}(x)\right] ^{1/2}\\= & {} 2\left[ 2q_n(x)+(x^2+2x)+r_n(x)\right] \omega ^*\left( f^{\prime \prime },n^{-1/2}\right) , \end{aligned}$$

where

$$\begin{aligned} r_n(x)=n^2\left[ G_n\left( \left( e^{-x}-e^{-t}\right) ^4,x\right) \cdot T^G_{n,4}(x)\right] ^{1/2}. \end{aligned}$$

Thus the proof of theorem is complete. $\square$

Remark 2

By direct calculations can be obtained the following results

• (i) $\displaystyle \lim _{n\rightarrow \infty }n^2 T_{n,4}^{G}(x)=3x^2(x+2)^2,$

• (ii) $\displaystyle \lim _{n\rightarrow \infty } n^2 G_n\left( \left( e^{-x}-e^{-t}\right) ^4,x\right) =3x^2(x+2)^2e^{-4x}.$

As a consequence of the Theorem 2 and Remark 2 can be obtained the following result:

Corollary 1

Let $f,f^{\prime \prime }\in C^*[0,\infty )$, then for $x\in [0,\infty )$ we have

$$\begin{aligned} \lim _{n\rightarrow \infty } n\left[ G_n(f,x)-f(x)\right]= & {} -\left( ax+bx+\frac{ax^2}{2}+\frac{bx^2}{2}\right) f^\prime (x) \\&+\left( x+\frac{x^2}{2}\right) f^{\prime \prime }(x). \end{aligned}$$