1 Introduction

Superlattices offer possibilities to study transport (Wacker 2002) and optical (Pereira 1995) properties of semiconductor under controlled conditions. This paper uses the anisotropic medium approach that can be easily programmed and includes the main many body effects required to describe steady state nonlinear absorption. The expressions delivered reduce exactly to Elliott’s formula in the low density linear limit. This leads to an efficient numerical tool to investigate new materials, starting e.g. from ab initio calculations. This has potential for a major impact in the development of new materials with applications from terahertz (THz) and mid-infrared (MIR) to the visible (VIS) spectral range (Pereira 2015). The superlattices are modelled as anisotropic media characterized by effective masses parallel and perpendicular to the growth direction (Pereira 1995). That suggests that new materials being currently investigated for solar cells and which are strongly anisotropic (Steinmann et al. 2015), may also be very useful for nonlinear optics applications, e.g. the controllable anisotropy in the superlattice case might be useful for applications such as power limiting (Poirier et al. 2002; Wu et al. 2003). Here the anisotropy-induced nonlinearity in the nanostructure is controlled per design in contrast with less controllable recent studies in which it depends on the nanoparticle shape (Hua et al. 2015). We show that the nonlinearities increase with the anisotropic character, but the results are only valid as long as sufficient tunnelling occurs. In other words, isolated quantum wells should not be addressed by this method. This paper extends and complements the study in Pereira (2016) with different well widths and a more detailed analysis of the population inversion and is organized as follows: first, the main equations used are summarized. Next, numerical applications for GaAs/AlGaAs superlattices are given and a short summary follows.

2 Mathematical approach and model equations

The carrier-induced optical nonlinearities of semiconductors can be obtained by the self-consistent evaluation of Many Body Nonequilibrium Green’s Functions (NEGF). Efficient numerical methods used here have been successfully applied to both inter-subband (Pereira and Faragai 2014; Pereira 2007, 2008, 2011; Pereira et al. 2007; Pereira and Tomić 2011) and inter-band transitions (Grempel et al. 1996; Pereira et al. 1994; Pereira and Henneberger 1997; Chow et al. 1992) in quantum wells and superlattices. For completeness, we repeat here the main equations of Pereira (2016) for a guide to the reader, by starting with the interband polarization that has been used to describe superlattices as an effective anisotropic 3D material (Pereira 1995),

$$\left[ {\hbar \omega + i\Gamma - E_{g} \left( \gamma \right) - \frac{{\hbar^{2} k^{2} }}{{2\mu_{\parallel } }}\xi \left( {\theta ,\gamma } \right)} \right]P\left( {\vec{k},\omega } \right) = A\left( \omega \right)\left[ {\wp \cdot E\left( \omega \right) + \mathop \sum \limits_{{\vec{k}^{{\prime }} \ne \vec{k}}} {\mathcal{W}}_{{\vec{k} - \vec{k}^{{\prime}} }} P\left( {\vec{k}^{{\prime }} ,\omega } \right)} \right],$$
(1)

where the meaning of the anisotropy dependent bandgap is explained below and ξ(θ, γ) = sin 2 θ + γcos 2 θ. The anisotropy parameter γ is given by the ratio between the in-plane \(\mu_{\parallel }\) and perpendicular \(\mu_{ \bot }\) reduced effective masses, \(\gamma = {{\mu_{\parallel } } \mathord{\left/ {\vphantom {{\mu_{\parallel } } {\mu_{ \bot } }}} \right. \kern-0pt} {\mu_{ \bot } }}\), with \(\frac{1}{{\mu_{\parallel } }} = \frac{1}{{m_{e\parallel } }} + \frac{1}{{m_{h\parallel } }}\) and \(\frac{1}{{\mu_{ \bot } }} = \frac{1}{{m_{e \bot } }} + \frac{1}{{m_{h \bot } }}\) which are calculated from the non-interacting superlattice Hamiltonian \({\mathcal{H}}_{0}\), \(\frac{1}{{m_{i\parallel } }} = \hbar^{ - 2} \partial^{2} /\partial k_{i\parallel }^{2}\Psi \left| {{\mathcal{H}}_{0} } \right|\Psi\), \(\frac{1}{{m_{i \bot } }} = \hbar^{ - 2} \partial^{2} /\partial k_{i \bot }^{2}\Psi \left| {{\mathcal{H}}_{0} } \right|\Psi\), for i = e, h. More details are given in Pereira (1995). A phenomenological scattering rate \(\Gamma\) is used to simulate the average dephasing that stems from the electron–electron, electron–phonon and electron-impurity scattering (Chow et al. 1992; Schmielau and Pereira 2009a, b), in order to keep the approach as simple as possible without affecting the conclusions. We have neglected any k-dependence on the transition dipole moment \(\wp\) induced by the electric field E(ω). In a superlattices there is a preferred direction determined by the growth (z-direction), leading to cylindrical symmetry. The next step is to perform an angle average, \(\left\langle {\upxi\left( {\uptheta,\upgamma} \right)} \right\rangle = \left\langle {\sin^{2}\uptheta +\upgamma\cos^{2}\uptheta} \right\rangle = \frac{1}{2}\left( {1 +\upgamma} \right)\) and thus

$$\frac{{\hbar^{2} k^{2} }}{{2\mu_{\parallel } }}\xi \left( {\theta ,\gamma } \right) \to \frac{{\hbar^{2} k^{2} }}{{2M_{\parallel } }}.$$
(2)

The resulting anisotropic mass \(M_{\parallel } = 2\mu_{\parallel } /\left( {1 + \gamma } \right)\) determines the exciton Bohr radius a 0 and corresponding 1S binding energy E 0,

$$a_{0} = a_{0} \left( \gamma \right) = \hbar^{2} \epsilon_{0} /e^{2} M_{\parallel } ,\quad E_{0} = E_{0} \left( \gamma \right) = 2Ry /\left( {1 + \gamma } \right),\quad Ry = \frac{{\mu_{\parallel } e^{4} }}{{2\hbar^{2} \epsilon_{0}^{2} }},$$
(3)

where ϵ 0 and e denote, respectively the background dielectric constant and the electron charge. The resulting exciton binding energies in superlattices are in very good agreement with experiments, as demonstrated in Pereira (1995).

By approximating the full inversion factor by \(A\left( \omega \right) = \tanh \left[ {\beta \left( {\hbar \omega - \mu } \right)/2} \right]\) we make sure that the cross-over from absorption to gain takes place exactly at the total chemical potential. Next, we replace the usual Yukawa potential describing screened carriers in 3D (which does not have analytical solutions for the corresponding Schrödinger equation) by the Hulthén potential \({\mathcal{W}}\left( r \right) = - 2e^{2} \kappa \epsilon_{0}^{{{\prime } - 1}} /\left( {{ \exp }(2\kappa r) - 1} \right)\) (Pereira 1995; Bányai and Koch 1986; Flügge 1974), which has successfully reproduced bulk nonlinear optical spectra (Schmielau and Pereira 2009c) and has well known analytical solutions.

The total chemical potential μ = μ e  + μ h and screening wavelength \(\kappa = \kappa_{e} + \kappa_{h}\) are given by

$$\beta \mu_{\lambda } = ln\nu_{\lambda } + K_{1} \ln \left( {K_{2} \nu_{\lambda } + 1} \right) + K_{3} \mu_{\lambda } ,$$
(4)
$$\kappa_{\lambda } = \sqrt {\frac{{4\pi e^{2} }}{{\epsilon_{0} }}\frac{{\partial n_{\lambda } }}{{\partial \mu_{\lambda } }}} = \sqrt {\frac{{\beta \pi e^{2} n_{\lambda } /\epsilon_{0} }}{{\frac{1}{{\nu_{\lambda } }} + \frac{{K_{1} K_{2} }}{{K_{2} \nu_{\lambda } + 1}} + K_{3} }}} ,$$
(5)

where K 1 = 4.897, K 2 = 0.045 and K 3 = 0.133. The parameter ν λ is obtained from the particle density for electrons and holes, n = n e  = n h by \(\nu_{\lambda } = 4n_{\lambda } /\left[ {\left( {2m_{\parallel ,\lambda } /\beta \pi \hbar^{2} } \right)\left( {2m_{ \bot ,\lambda } /\beta \pi \hbar^{2} } \right)^{1/2} } \right]\) and β = 1/K B T (Pereira 1995).

It is beyond the scope of this paper to show the intermediate details that lead Eq. (6). The main steps are to combine the partly phenomenological approach of Bányai and Koch (1986) with the material parameters calculated with the anisotropic medium approach (Pereira 1995; Pereira et al. 1990). Furthermore, we use hypergeometric functions instead of the Jost function approach of Pereira (1995) and Flügge (1974). The resulting absorption spectrum then reads

$$\alpha \left( \omega \right) = \alpha_{0} \left( \gamma \right)\frac{\hbar \omega }{{e_{0} }}\tanh \left[ {\beta \left( {\hbar \omega - \mu } \right) /2} \right]\left\{ {\mathop \sum \limits_{n = 1}^{\sqrt g } \frac{4\pi }{n}\left( {\frac{1}{{n^{2} }} - \frac{{n^{2} }}{{g^{2} }}} \right)\delta_{\Gamma } \left( {\Delta - e_{n} } \right) +\, 2\pi \int\limits_{0}^{\infty } {\frac{{\sinh \left( {\pi g\sqrt x } \right)}}{{\cosh \left( {\pi g\sqrt x } \right) - \cos \left( {\sqrt {4g - g^{2} x} } \right)}}\delta_{\Gamma } \left( {\Delta \left( { - x} \right)} \right)dx} } \right\},$$
(6)

where \(\alpha_{0} \left( \gamma \right) = 2\wp^{2} /\left( {n_{b} \hbar ca_{3}^{0} \left( \gamma \right)} \right)\). The normalized detuning is \(\Delta = \left( {\hbar \omega - E_{g} \left( \gamma \right)} \right) - E_{0} \left( \gamma \right)\). Here, and c denote, respectively, the background refractive index and the speed of light in vacuum. In Eq. (6) above, the band gap renormalization stems from the Mott criterion. This expression for the bandgap renormalization is usually in good agreement with the full Green’s function approach and the Single Plasmon Pole Approximation (SPPA) simplified under a quasi-static approximation (Pereira 1995).

$$E_{g} \left( \gamma \right) = E_{gap} + E_{0} \left( \gamma \right)\left\{ {\begin{array}{*{20}l} { - 1 + \left( {1 - \frac{1}{g\left( \gamma \right)}} \right)^{2} , } \hfill & {g\left( \gamma \right) \ge 1} \hfill \\ { - 1/g\left( \gamma \right) ,} \hfill & {g\left( \gamma \right) < 1} \hfill \\ \end{array} } \right.$$
(7)

where \(g\left( \gamma \right) = 1/\kappa a_{0} \left( \gamma \right)\) and \(E_{gap} = E_{c} \left( 1 \right) + E_{HH} \left( 1 \right) + E_{gap,bulk}\) is the bulk (temperature dependent) isotropic bandgap found in semiconductor material tables in the literature plus the confinement energies of the lowest conduction subband and the top heavy hole subband.

The broadened delta function representation is \(\delta_{\Gamma } \left( x \right) = 1/\pi \delta \eta cosh(x /\eta )\), where \(\upeta =\Gamma /E_{0} \left( \gamma \right)\) which reproduces the Urbach tail very efficiently. The sum in the exciton part runs through the available states within the largest integer value of \(\sqrt {g\left( \gamma \right)}\). In the low density limit, g(γ) → ∞ and we recover the Elliot formula for excitonic luminescence with the correct balance between bound and continuum states.

3 Numerical results and discussion

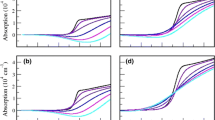
Figure 1 depicts the nonlinear optical absorption of GaAs–Al0.3Ga0.7As superlattices at T = 300 K. The scaled photon energy (x-axis) highlights the Coulomb correction effects that would otherwise be mixed with the changes due to carrier confinement by increasing the well width, included in \(E_{gap} = E_{c} \left( 1 \right) + E_{HH} \left( 1 \right) + E_{gap,bulk}\).

Fig. 1
figure 1

Nonlinear optical absorption of GaAs–Al0.3Ga0.7As superlattices at 300 K with increasing anisotropy characterized by decreasing γ = 0.61, 0.42, 0.20 and 0.11, respectively from a–d. This is obtained by fixing the barrier width at 6 nm and increasing the well width correspondingly by 1, 2, 4 and 6 nm. In each panel, from top to bottom the carrier density in both conduction and valence bands is N = 0, 0.1, 0.5, 1, 1.5 and 2 × 1018 cm−3. E0,b = 4.2 meV is the bulk GaAs exciton binding energy. From a–d, Egap = 2.092, 2.0135, 1.918, 1.873 eV

Full size image

The increase in anisotropy (smaller γ) by increasing the quantum well length, stems from reducing the wavefunction overlap through the barrier, here measured by a larger mass along the growth direction. The single quantum well case would be obtained for a very large barrier, with \(\mu_{ \bot }\to \infty\) and correspondingly \(\gamma \to 0\). However, this method should not be used in the quasi-2D case and calculations dedicated to quantum wells (see e.g. Pereira et al. 1994) should be used. From (a) to (d) we do see an increase in nonlinearity, i.e. a larger reduction in absorption with increasing carrier density. Note that even though Pereira (1995) also has analytical expressions for the nonlinear spectra of superlattices, to the best of that author’s knowledge numerical applications have never been given before as in the present paper. Figure 2 makes it more clear by showing the differential absorption \(\Delta \alpha \left( \omega \right) = \alpha \left( {\omega ,N} \right) - \alpha \left( {\omega ,N = 0} \right)\).

Fig. 2
figure 2

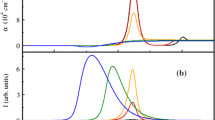
Differential absorption \({\Delta \alpha }\left(\upomega \right) =\upalpha\left( {\upomega,{\text{N}}} \right) -\upalpha\left( {\upomega,{\text{N}} = 0} \right)\) for the structures in Fig. 1 with a carrier density N = 1×1017 cm−3 at 300 K. The solid, dashed, dot-dashed and dot-double dashed correspond to an increase in anisotropy, characterized respectively by γ = 0.61, 0.42, 0.20 and 0.11

Full size image

Figure 3 allows a better understanding of the excitonic bleaching and gain development as a function of anisotropy and carrier density.

Fig. 3
figure 3

Inverse screening length κ (a) and total chemical potential βμ (b) as a function of carrier density for the same structures in Figs. 1 and 2 at 300 K. The solid, dashed, dot-dashed and dot-double dashed correspond to an increase in anisotropy, characterized respectively by γ = 0.61, 0.42, 0.20 and 0.11

Full size image

The combined figures show that as the anisotropy increases (smaller γ, so does the inverse screening length κ leading to a faster reduction of the screened Coulomb interaction and consequently larger optical nonlinearity, measured here directly by the differential absorption. This shows that an increase in nonlinearity is observed for all carrier densities, which are considered in the manuscript, and in the whole range of energies depicted in Fig. 1. Note however that it only makes sense to consider the range of linear to saturated absorption in the differential transmission calculations while two positive values are compared. The negative absorption (gain) confuses the comparison.

By increasing the anisotropy, the z-direction electron and hole masses become too different, with a much larger increase in hole mass. When the upper and lower (average) curvatures or equivalently, the average effective masses are too different the total chemical potential is relatively smaller (see Fig. 3b) and so is the inversion factor \(A\left( \omega \right) = \tanh \left[ {\beta \left( {\hbar \omega - \mu } \right)/2} \right]\) of Eqs. (1) and (6), thus reducing the gain in Fig. 1. This influence of different electron and hole masses on the inversion/gain is fully consistent with the detailed analysis for isolated quantum wells seen e.g. in Pereira and Henneberger (1997). The results are complemented by a two-dimensional plot of the population inversion factor as a function of detuning and anisotropy parameter in Fig. 4.

Fig. 4
figure 4

Population inversion factor A(ω) of Eq. (1) as a function of detuning and anisotropy parameter at 300 K. The left and right panels are respectively for population densities N = 0.02 and 2 × 1018 cm−3

Full size image

Note the larger inversion region and values (the factor gets more negative) for smaller anisotropy (larger γ). The method used here can be used for a variety of other materials and superlattices as long as tunnelling between adjacent periods allows a 3D-like spread of carriers wavefunctions—either electrons or holes so that movement along the z-direction is possible and an effective 3D medium can be considered with corresponding effective masses. Thus the model is better suited for absorption in superlattices far from the 2D limit. In the quasi-2D limit of quantum wells, the full numerical solution (Grempel et al. 1996; Pereira et al. 1994; Pereira and Henneberger 1997) should be used. Thus, increase in nonlinearity is clearly demonstrated, which may be very important for truly 3D anisotropic new materials, but the high gain in quantum wells cannot be described by the method presented here.

In summary, the analytical expressions developed confirm the connection between an increase in optical nonlinearity with anisotropy by directly controlling the anisotropy and evaluating the resulting differential absorption and nonlinear spectra. This study illustrates the potential for three dimensional strongly anisotropic semiconductors materials for a role in nonlinear optics and a possible recipe to improve their efficiency by controlling the anisotropy.