Skip to main content
SpringerLink
Log in

Fitted finite difference method for singularly perturbed delay differential equations

  • Original Article
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

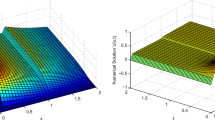
This paper deals with singularly perturbed initial value problem for linear second-order delay differential equation. An exponentially fitted difference scheme is constructed in an equidistant mesh, which gives first order uniform convergence in the discrete maximum norm. The difference scheme is shown to be uniformly convergent to the continuous solution with respect to the perturbation parameter. A numerical example is solved using the presented method and compared the computed result with exact solution of the problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bellman, R., Cooke, K.L.: Differential-Difference Equations. Academy Press, New York (1963)

    MATH  Google Scholar 

  2. Driver, R.D.: Ordinary and Delay Differential Equations. Springer, Belin- Heidelberg, New York (1977)

    MATH  Google Scholar 

  3. Bellen, A., Zennaro, M.: Numerical Methods for Delay Differential Equations. Oxford University Press, Oxford (2003)

    Book  MATH  Google Scholar 

  4. MacCartin, B.J.: Exponential fitting of the delayed recruitment/renewal equation. J. Comput. Appl. Math. 136, 343–356 (2001)

    Article  MathSciNet  Google Scholar 

  5. Derstine, M.W., Gibbs, F.A.H.H.M., Kaplan, D.L.: Bifurcation gap in a hybrid optical system. Phys. Rev. A 26, 3720–3722 (1982)

    Article  Google Scholar 

  6. Longtin, A., Milton, J.: Complex oscillations in the human pupil light reflex with mixed and delayed feedback. Math. Biosci. 90, 183–199 (1988)

    Article  MathSciNet  Google Scholar 

  7. Mackey, M.C., Glass, L.: Oscillation and chaos in physiological control systems. Science 197 287–289 (1977)

    Article  Google Scholar 

  8. Doolan, E.R., Miller, J.J.H., Schilders, W.H.A.: Uniform Numerical Methods for Problems with Initial and Boundary Layers. Boole Press, Dublin (1980)

    MATH  Google Scholar 

  9. Farrell, P.A., Hegarty, A.F., Miller, J.J.H., O’Riordan, E., Shishkin, G.I.: Robust Computational Techniques for Boundary Layers. Chapman-Hall/CRC, New York (2000)

    MATH  Google Scholar 

  10. Roos, H.G., Stynes, M., Tobiska, L.: Numerical Methods for Singularly Perturbed Differential Equations. Convection-Diffusion and Flow Problems. Springer, Berlin (1996)

    MATH  Google Scholar 

  11. Amiraliyev, G.M., Mamedov, Y.D.: Difference schemes on the uniform mesh for singularly perturbed pseudo-parabolic equations. Tr. J. Math. 19, 207–222 (1995)

    MATH  MathSciNet  Google Scholar 

  12. Amiraliyev, G.M., Duru, H.: A uniformly convergent finite difference method for a initial value problem. Appl. Math. Mech. 20(4), 363–370 (1999)

    Article  MathSciNet  Google Scholar 

  13. Amiraliyev, G.M., Erdogan, F.: Uniform numerical method for singularly perturbed delay differential equations. J. Comput. Math. Appl. 53, 1251–1259 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  14. Tian, H.: The exponential asymptotic stability of singularly perturbed delay differential equations with a bounded lag. J. Math. Anal. Appl. 270, 143–149 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  15. Maset, S.: Numerical solution of retarded functional differential equations as abstract Cauchy problems. J. Comput. Appl. Math. 161, 259–282 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  16. Mallet-Paret, J., Nussbaum, R.D.: A differential-delay equations arising in optics and physicology. SIAM J. Math. Anal. 20, 249–292 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  17. Lange, C.G., Miura, R.M.: Singular perturbation analysis of boundary-value problems for differential-difference equations. v. small shifts with layer behavior. SIAM J. Appl. Math. 54, 249–272 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  18. Lange, C.G., Miura, R.M.: Singular perturbation analysis of boundary-value problems for differential-difference equations. vi. small shifts with rapid oscillations. SIAM J. Appl. Math. 54, 273–283 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  19. Lange, C.G., Miura, R.M.: Singular perturbation analysis of boundary-value problems for differential difference equations. SIAM J. Appl. Math. 42, 502–531 (1982)

    Article  MATH  MathSciNet  Google Scholar 

  20. Kadalbajoo, M.K., Sharma, K.K.: Numerical analysis of boundary-value problems for singularly-perturbed differential-difference equations with small shifts of mixed type. J. Optim. Theory Appl. 115, 145–163 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  21. Kadalbajoo, M.K., Sharma, K.K.: Numerical analysis of singularly perturbed delay differential equations with layer behavior. Appl. Math. Comput. 157, 11–28 (2004)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Sciences, Yuzuncuyil University, 65080, Van, Turkey

    Fevzi Erdogan

  2. Department of Mathematics, Faculty of Sciences, Sinop University, 57000, Sinop, Turkey

    Gabil M. Amiraliyev

Authors
  1. Fevzi Erdogan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gabil M. Amiraliyev
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fevzi Erdogan.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Erdogan, F., Amiraliyev, G.M. Fitted finite difference method for singularly perturbed delay differential equations. Numer Algor 59, 131–145 (2012). https://doi.org/10.1007/s11075-011-9480-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-011-9480-7

Keywords

Search

Navigation