1 Introduction

As is well known by now, the novel severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and resulting coronavirus disease 2019 (COVID-19) was first reported in Wuhan city, Hubei province, China in early December 2019. The rapid spread of the disease to other countries led World Health Organization (WHO) to declare it a global pandemic in March 2020. Since then, COVID-19 has caused over 6.2 million fatalities and presented unprecedented challenges to healthcare systems even in well-developed countries in addition to causing major disruptions to the economy all around the world [1].

Analysis of data related to COVID-19 shows that the propagation of this disease is governed by a nonlinear multi-variable dynamic process that depends on a broad range of variables. These variables are dependent on the social, governmental, economic, and environmental situations in addition to being influenced strongly by human activities. Further exploration of worldwide data shows cumulative interactions of these variables that make it challenging to identify their individual effects from the data. Given this complexity, analytical epidemiological modeling is of high significance since it can serve as a valuable tool for uncovering how individual variables contribute to the overall dynamics. In addition, accurate modeling and dynamic analysis of the infection spreading provides deeper insight and identification of the most influential variables. Specifically, considering the variation of these variables in different target populations, e.g., cities, states, countries, and continents provide insightful demographic information about the propagation of the disease. These insights can serve as a valuable basis for designing control strategies for COVID-19 as well as for many more pandemics that will certainly arise in the future.

Over the past two years, the efficacy of various strategies, both pharmaceutical and non-pharmaceutical have been evaluated. For example, it has been repeatedly shown that self-isolation and lockdown greatly limit the rate of infections thereby decreasing the peak load on the national healthcare systems. As we know, reducing the peak loads prevent the healthcare systems from getting overwhelmed leading to higher survival rates. Also, beneficial effects of massive and rapid vaccination on the spread of infection, severity of symptoms and illness duration were evidenced as well. However, clarifying the role of seasonality in modeling the disease spread and proposed control strategies are still far from mature. It would arguably improve our understating about the fluctuations, trends, and patterns that occur or repeat over a specific period of time in an epidemic [2]. The extracted information also can be used for long-term planning by determining the probability of different equilibrium points to predict whether it is surging, receding, or evolving into an endemic equilibrium. Also, as was mentioned, the demographic analysis would be insightful with regard to medical and behavioral variables such as vaccination and social distancing in each target population as well. Another important aspect of this temporal analysis concerns the biological characteristics of the disease. Indeed, observing seasonality in infectious over time can be informative about the biological parameters of the host-microbe interaction, including the prevalence of the disease among infected individuals, infection contagiousness, diagnostic capacity, and size of the susceptible population as well [3].

There has been a profusion of publications focusing on data-based modeling, too many in fact to document here. While these efforts are laudable and can lead to some understanding of immediate trends, their contribution towards gaining insight are very limited. In addition, an over emphasis on including every variable possible impedes the interpretability of the analysis results. Such an approach may also increase the risk of missing identification of causalities due to artifact effects of data and corresponding correlations. As a remarkable case in point, a recent study analyzed seasonality and corresponding oscillations in infected individuals in New York City, NY, and Los Angeles, CA, where very similar oscillations can be seen in data related to the number of new cases. This observed statistical similarity, analyzed by purely data-based modeling, would easily mislead the process of decision-making and planning into formulating the same policy, for example. In fact, further exploration actually revealed a key demographic driving variable that turned out to be the daily variation in the number of tests in each region [3]. Further, as another example, the artifact of intermittent reporting led one to believe that there were puzzling oscillations in mortality data [4]. Many other factors can adversely affect the accuracy of pure-data-based analysis as well; for example, several studies pointed out a significant local delay in reporting the number of new infections and deaths [5].

In contrast to the above instances, there is a very long history of mathematical modeling of epidemiological phenomena dating back to early studies by Bernoulli in the eighteenth century [6, 7]. These models strive to explain the relevance of real historical observations and infectious disease dynamics within a mathematical framework. In fact, most current studies use models built upon those proposed in the 1930’s by Kermack and McKendrick [8, 9]. In general, these models known as compartment models include a set of nonlinear ordinary differential equations in which state variables represent the population numbers in different stages of the infectious disease spread [10]. Various epidemiological models were developed rapidly after Kermack’s original work [11].

Several notable modern textbooks discuss fundamental phenomena in mathematics of epidemiology. We refer the reader to them for a clearer understanding of the model assumptions, derivations, and implications [10, 12,13,14]. Hethcote’s paper [15] is another notable resource that provides intuitive information on the dynamics of this disease.

Non-periodic responses of compartmental models were analyzed in [16, 17] that represent progression toward an endemic equilibrium point. Effects of periodicity are most likely caused by actions such as opening and closure of public places, change of seasons, vacillations in social behavior, and new variants with varying infection rates. These have often been modeled using the concept of forced oscillations. In an early work by [18], the effects of seasonal fluctuations along with contact rate periodicity were studied. Another notable nonlinear phenomenon observed leading to periodic responses is Hopf bifurcation. The effects of model parameter values on the existence of locally asymptotically stable solutions and Hopf bifurcation were studied in [19]. It was shown that the occurrence of periodic solutions through Hopf bifurcations can mathematically be related to the presence of time delays and nonlinear incidence rates [20,21,22]. The effects of seasonal variations in the contact rate on the occurrence of infinite sub-harmonic bifurcations in epidemic models were investigated as well in [23]. Also, bifurcation was studied with the hospital resource as a varying parameter [24]. A comprehensive study of periodic and non-periodic dynamics of compartmental models is also discussed in [13].

Literature also shows that compartmental models were modified to analyze the seasonality and corresponding oscillation [15, 25, 26]. In [27] it is proved that under the assumption of a fixed population, SIR model and constant parameters, the model will show damped oscillation with a stable endemic point. In another category of study, the exogenous and endogenous mechanisms were incorporated in the modeling for temporal analysis [25]. The effects of these mechanisms on sustained oscillation were analyzed as well. It was shown that the exogenous mechanism causes oscillation by periodic forcing of the transmission term, while the endogenous mechanism can destabilize the model’s endemic equilibrium by adding delay terms [25].

Other studies tried to make the problem more realistic by canceling some of the modeling assumptions. For example, classical compartmental models are developed under the assumption of constant, random, and homogeneous mixing populations with indistinguishable individuals [28]. However, in real scenarios, each individual is in contact with a specific social network which means the number of potential contacts for each individual is significantly smaller than the total population size. Hence, in a different category of research, infectious diseases are modeled based on complex social network structures. The general idea is to abstract the population and corresponding connections in a network structure by nodes and links, respectively. Accordingly, the spread of diseases is modeled by a network of complex interactions between individuals [26, 29,30,31,32].

Other studies have investigated both temporal and spatial aspects of infectious diseases spread by developing compartmental models in a cellular automata framework, that aims to gain insight on the possibility of oscillations in different groups of the total population. Groups have been formed based on various criteria such as levels of social activity [33,34,35,36].

Another trend of research focuses on the mathematical abstraction of seasonality by considering time-dependent model parameters. A compartmental model with time-varying birth and death rates is one of the recent examples in this regard [4]. For further exploration, we suggest [37], which is a recent review that surveys the literature on seasonal dynamics.

In general, prophylactic measures for the control of infectious disease spread include vaccination, treatment, and isolation. Many studies focused on analyzing the dynamics of compartmental models with these measures and control strategies including non-pharmaceutical and pharmaceutical ones [38,39,40,41]. As notable examples, in [42, 43] optimal control and parameter tuning were studied with the aim of mitigating the disease. Other studies related to control strategies focused on the effects of infectious transmission. For example, various compartmental models with different transmission formulations were studied in [44, 45].

Literature also emphatically demonstrates that the vaccination policy, which is generally adopted by governments, is the principal component in the control of disease’s spread. It should be noted that vaccination will not fully protect an individual from infection, so there is always a probability for a vaccinated person to get infected. Even in the case of releasing antibodies in a host, some pathogens can mutate. It means that the immune system might not be able to defeat the infection. To characterize these issues and hence the level of protection that is provided by a vaccine in an individual, epidemiologists define the efficacy of any vaccine. Another notable factor is a personal decision. An individual decision about complying with vaccination policy is involved with the assessment of the risk of morbidity from vaccination and the probability of infection. In addition to risk, an individual’s willingness varies with other factors such as age, health conditions, lifestyle and profession. Each of them can provide insight into analyzing the dynamics of the disease spread, vaccination and decision making [46, 47]. Another factor affecting the vaccination is heterogeneity in the population’s response to the vaccine. In this condition, it is assumed that individuals respond differently to a vaccine that affects the dynamics of the epidemic. In [48] the global stability of the infection-free equilibrium state is mathematically formulated.

In this study, in order to provide a generic and interpretable abstraction of the dynamics of this disease, we consider an epidemiological model which makes a compromise between predictive accuracy and complexity. Instead of purely relying on data in modeling, we strive to understand its diversity over different target populations and seek to discover the principal parameters that contribute to this difference. In other words, instead of fitting the model simulation results to data, we use data for guiding and validating the analysis. We do believe that fundamental characteristics of dynamics of this disease along with the most influential variables can be accurately, effectively, and efficiently identified using a compact model. Such a parsimonious model provides a fundamental understanding of the dynamics of the disease that not only explains what happened so far but also predicts infectious progression and control.

It is important to note that this mechanistic approach of modeling COVID-19 and emphasizing the causalities in the arguments make the analysis more easily generalizable to future pandemics and outbreaks. There is ample support in the literature to make the case that such models have the highest potential and utility. In fact, they have been used to investigate a wide range of outbreaks including the SARS epidemic in 2002-2003 [49], H5N1 influenza outbreak in 2005 [50], the H1N1 influenza pandemic of 2009 [51] and the Ebola outbreak of 2014 [52]. With this perspective, we analyze the dynamics of this COVID-19 pandemic using a compartmental model. The effects of seasonality are incorporated in modeling the disease transmission. The corresponding forced oscillation is analyzed to investigate mutual interactions between transmission and seasonality characteristics, vaccination rate and efficacy, and different sources of immunity.

It should be noted that there are two major differences in developing vaccination models. The first difference concerns the vaccination class. In one approach, it is assumed that vaccination is equivalent to going through the disease and considers vaccinated individuals as recovered ones. That means, in the compartmental model there is no need for an additional class for vaccinated individuals. The second difference addresses the discrete and continuous vaccination. In the first approach, it is assumed that individuals enter the system at a point in their life upon vaccination or skipping vaccination and then are included in the susceptible class. School children are a notable example of a discrete approach. In the continuous approach, models provide for continuous vaccination of the population as long as they are in the system. In a real scenario, vaccination cannot be discrete since a vaccinated individual may get susceptible over time given the imperfection inherent in any vaccination [13]. In this study, with the continuous assumption in addition to consideration of vaccination efficacy, we study the effects of the seasonality of the disease with a periodic transmission rate as well.

The remaining parts of this paper are organized as follows. In Sect. 2, the model development is outlined. In Sect. 3, nonlinear analysis for disease-free and endemic equilibrium is investigated. In Sect. 4, discussion and summary of findings are presented and finally, we present a conclusion in Sect. 5.

2 Notes on mathematical models

First, we define the key variables used in epidemiological models. Although the definitions of the terms are found universally, we define them here for completeness.

  • Susceptible individuals. An individual is considered susceptible when there is no detectable level of pathogens in the body. Accordingly, the body’s immune system did not respond to the disease-causing pathogen, so the individual’s immune system has not yet developed a specific response to the disease-causing pathogen.

  • Exposed individuals. An exposed person had contact with an infected person and is infected; however, no obvious symptoms can be observed and the level of the pathogen is so low that it will not sustain transmission to the other host.

  • Infected individuals. The infected individual body has high enough amount of pathogens that he/she can transmit to other susceptible individuals.

  • Removed individuals. The individual immune system has defeated the infection and reduced the number of parasites significantly in which case the individual has recovered. In addition, isolation from the general population or death by the disease can contribute to this class. In all of these cases, the individual is said to be removed.

  • Immune individuals. An individual who is protected against the disease because of a vaccine or other sources of immunity.

The models are typically notated using initials, for example, SIR for Susceptible-Infectious-Removed. Without loss of generality, the number of individuals in each class is usually normalized with respect to a nominal, total population (as we do in this paper).

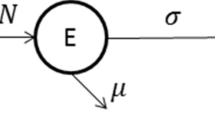
In our study, we consider the Susceptible-Infected-Immune (SII) framework. In this analysis, we assume that the total population size (denoted by N) remains relatively constant during pandemic based on the following reasoning. This analysis is carried out for a short period (a year or two), so we assume that the change in the total population due to the death of diseased and newborn babies is negligible during the analysis period. The change in the population owing to disease-related deaths and newborns is not substantial, unlike when a population used to experience diseases with decimating effects such as the plague, or when a pandemic is analyzed for a considerable period such as a decade or more. Therefore, it is reasonable to assume that the death and birth rates are not influential enough to alter the total population significantly over the period of the analysis. In this model, X, and Y represent the susceptible and infectious populations and Z represents the immune population. The immune population considered here is a combination of vaccine induced immune population and immunity of population obtained by the other sources that include natural immunity. This model (SII) is adopted and modified from a standard SIS model with vaccination as illustrated in Fig. 1 [13] and is defined as follows.

$$\begin{aligned} \begin{array}{lll} X'&{}=\varLambda -{\beta X Y}-(\mu +\psi )X+\chi \gamma Y, \\ Y'&{}={\beta X Y}+{\beta \delta Z Y}- (\mu +\gamma )Y, \\ Z'&{}=\psi X-{\beta \delta Z Y}+(1-\chi )\gamma Y-\mu Z, \end{array} \end{aligned}$$
(1)

where, \('\) denotes derivative with respect to time.

In this model, \(\varLambda \) is the birth rate, \(\mu \) is the death rate, \(\gamma \) is the recovery rate, \(\beta \) is the transmission rate, \(\psi \) is the vaccination rate, \(\chi \) is the proportion of individuals who recover to the immune class due to immunity other than vaccine-induced immunity, \(1-\chi \) is the proportion of individuals who recover to the susceptible class, \(\delta \) is the vaccine reduction coefficient, where \(0\le \delta \le 1\). If \(\delta =0\) the vaccination is perfect. \(\epsilon =1-\delta \) is hence the vaccine efficacy.

Figure 1 illustrates the Susceptible-Infected-Immune model. In practice, the vaccine is applied to healthy individuals, so only susceptible individuals get vaccinated (\(\psi X\)). \({\beta X Y}\) is the number of secondary infections of susceptible individuals. \({\beta \delta Z Y}\) is the number of secondary infections of vaccinated individuals with an imperfect vaccine. \(\chi \gamma Y\) is the number of individuals who recover to the immune class due to immunity other than vaccine-induced immunity. \((1-\chi ) \gamma Y\) is the number of individuals who recover to the susceptible class. \(\mu X\), \(\mu Y\) and \(\mu Z\) are the number of individuals removed from susceptible, infected, and immune classes.

Fig. 1
figure 1

Susceptible-infected-immune model

Full size image

Although the exact reasons for the dynamic behavior of an endemic disease like COVID-19 are not precisely known, we can indulge in some rational speculation. Some of the reasons plausibly include imperfect vaccines, environmental factors, new variants of the virus (with different infection rates), social and biological factors, such as population density, social distancing policies, and governmental actions. In [53], researchers hypothesized that autonomous models exhibit dynamic behavior intrinsically and oscillate for a constant value of transmission rate, \(\beta \). In practice, it is difficult to explain the dynamic behavior of the disease with a constant value of \(\beta \). Recent studies suggest that the dynamic behavior can be fairly explained by taking a periodic transmission rate [54]. Therefore, to incorporate the dynamic behavior of the disease, we define the transmission rate as a combination of static and dynamic parts [54], in which the dynamic part is a periodic function of time t. The transmission rate \(\beta \) is consequently given by

$$\begin{aligned} \begin{array}{ll} \beta =\beta _{0}\Bigg [1+\beta _{1}\cos \Big (\varOmega t+\phi )\Big )\Bigg ], \end{array} \end{aligned}$$
(2)

where, \(\varOmega =\frac{2\pi }{T}\), \(\beta _{0}\) and \(\beta _{1}\) are amplitudes of the static and dynamic transmission rates, respectively, T is the time period and \(\phi \) is the phase difference between static and dynamic phases. The initial infections take some time to accelerate and transmit to the masses; this delay between static and dynamic phases is captured by \(\phi \). Note that, in reality, we witnessed the dynamic behavior of COVID-19 with several combinations of harmonics for different countries around the world. In this paper, however, we approximate the transmission rate to the first harmonic for simplicity. Through this rather simple abstraction, we seek to explain the various reasons that affect the dynamic behavior of the disease. Our future work will perhaps consider a Fourier series-based model with higher harmonics.

3 Nonlinear analysis

This section focuses on the analysis of extinction or persistence of the disease which is determined by the stability of the disease-free equilibrium and the existence of endemic equilibrium. Investigation of the dynamic behavior and vaccination-based control of COVID-19 epidemics require a sound understanding of the mode of dissemination as well as the impacts of control strategies. In order to investigate the dynamic behavior, we need to consider various factors that affect it including perfect and imperfect vaccination.

Although in this work we do not include a quantitative comparison of results to actual observations, the parameters, birth rate (\(\varLambda \)), death rate (\(\mu \)) (per year: \(\varLambda \)=\(\mu =0.0014\), per day: \(\varLambda \)=\(\mu =0.0014/365\)), vaccination rate (\(\psi \)) (per year: \(\psi =0.64\), per day: \(\mu =64/365\)), transmission rate (\(\beta _{0}=1.6286\), \(\beta _{1}=0.8143\)) are chosen for a start basing them on realistic and approximate parameter values of the current COVID-19 epidemic in the U.S. [55]. The data of COVID-19 is used for high-level guidance of mathematical models while focusing on commonalities of internal transmission between different countries. To make the analysis independent of specific and local aspects of the transmission in each country, we neglect the temporary and short-lasting variance in the data. Therefore, the values of various periods and phases are selected based on analyzing the data of major countries such as the USA, China, India, the UK, and Germany [55]. In order to generalize the discussion, the statistical information of the most frequent/dominant trends across all these countries is extracted and quantified by numerical values of the phase and period. In fact, these values can be considered as principal values that drive the most frequent/dominant trend of COVID-19.

3.1 Disease-free equilibrium

We normalize susceptible, infected and immune in Eq. (1) such that \(x=\frac{X}{N}\), \(y=\frac{Y}{N}\) and \(z=\frac{Z}{N}\). The rescaled equations are as follows.

$$\begin{aligned} \begin{array}{lll} x'&{}=\varLambda -{\beta x y}-(\mu +\psi )x+\chi \gamma y, \\ y'&{}={\beta x y}+{\beta \delta z y}- (\mu +\gamma )y, \\ z'&{}=\psi x-{\beta \delta z y}+(1-\chi )\gamma y-\mu z. \end{array} \end{aligned}$$
(3)

In order to determine the equilibrium points, we set the time derivatives to zero and solve the corresponding algebraic equations. The disease-free equilibrium is obtained by setting \(y=0\) in Eq. (3) and is given by

$$\begin{aligned} \begin{array}{ll} E^{0}=\Bigg (\frac{\varLambda }{\mu +\psi },0,\frac{\psi \varLambda }{\mu (\mu +\psi )}\Bigg ). \end{array} \end{aligned}$$
(4)

We compute the Jacobian at the disease-free equilibrium:

$$\begin{aligned} J(E^{0})=\left( \begin{array}{ccc} -(\mu +\psi ) &{} -\beta x^{0}+\chi \gamma &{} 0 \\ 0 &{} \beta x^{0}+\beta \delta z^{0}-(\mu +\gamma )&{} 0 \\ \psi &{} -\beta \delta z^{0}+(1-\chi )\gamma &{} -\mu \\ \end{array} \right) . \end{aligned}$$
(5)

The eigenvalues of the Jacobian are \(-\mu \), \(-(\mu +\psi )\) and \(\beta s^{0}+\beta \delta v^{0}-(\mu +\gamma )\). For disease-free equilibrium to be stable, \(\beta x^{0}+\beta \delta z^{0}-(\mu +\gamma )=0\). We then define the reproduction number considering perfect vaccination (\(\delta =0\)) and imperfect vaccination (\(\delta \ne 0\)) as follows.

$$\begin{aligned} \begin{array}{ll} R(\psi _{p})=\frac{\beta \varLambda }{(\mu +\gamma )(\mu +\psi )},\qquad R(\psi )=\frac{\beta \varLambda (\mu +\delta \psi )}{\mu (\mu +\gamma )(\mu +\psi )}. \end{array} \end{aligned}$$
(6)

In the absence of the vaccination rate \(\psi =0\), the reproduction number is given by

$$\begin{aligned} \begin{array}{ll} R_{0}=\frac{\beta \varLambda }{\mu (\mu +\gamma )}. \end{array} \end{aligned}$$
(7)

Note that the reproduction number is an all-important parameter and determines whether or not the disease is extinguished. In particular, the reproduction number needs to be less than 1 for the disease-free equilibrium to be stable; in other words, for a disease to be eradicated.

From Eq. (6), one can see that the higher the vaccination rate, the smaller the reproduction number such that \(\lim _{\psi \rightarrow \infty }R(\psi )=\delta R_{0}\). Thus, if the vaccination efficiency \((\epsilon =1-\delta )\) is not high, \(R(\psi )\) cannot be less than one. The eradication of disease with imperfect vaccination exists only if \(\delta R_{0}<1\), if the vaccine efficiency satisfies \(\epsilon >(1-\frac{1}{R_{0}})\). If \(\delta R_{0}<1\), then there exists a critical vaccination level \(\psi ^{*}\) such that \(R(\psi ^{*})=1\). Using Eqs. (6) and (7), critical vaccination level for eradication of the disease is given by

$$\begin{aligned} \psi ^{*}=\frac{(R_{0}-1)\mu }{1-\delta R_{0}}. \end{aligned}$$
(8)
Fig. 2
figure 2

Response of the system for a disease-free equilibrium situation for \(R(\psi )=0.74\), \(\mu =3.93\times 10^{-06}\), \(\gamma =0.2\), \(\chi =0.8\), \(\psi =0.0313\), \(\delta =0.05\), \(\beta _{0}=1.6286\), \(\beta _{1}=0.8143\), \(T=360\), \(\phi =2.4435\)

Full size image

Figure 2 illustrates a disease-free equilibrium situation for a very high vaccination rate of \(\psi =0.0313\) and for the parameters \(\mu =3.93\times 10^{-06}\), \(\gamma =0.2\), \(\chi =0.8\), \(\delta =0.05\), \(\beta _{0}=1.6286\), \(\beta _{1}=0.8143\), \(T=360\), \(\phi =2.4435\). The reproduction number evaluated for this situation is \(R(\psi )=0.74\). Therefore, with a very high vaccination rate and nearly perfect vaccine (\(\delta =0.05\)),we can eradicate the disease completely.

3.2 Endemic equilibrium

To compute the expression of the equilibrium points for endemic equilibrium, the time derivatives in Eq. (3) are set to zero and the resulting equations are as follows.

$$\begin{aligned} \begin{array}{lll} 0&{}=\varLambda -{\beta x y}-(\mu +\psi )x+\chi \gamma y, \\ 0&{}={\beta x y}+{\beta \delta z y}- (\mu +\gamma )y, \\ 0&{}=\psi x-{\beta \delta z y}+(1-\chi )\gamma y-\mu z. \end{array} \end{aligned}$$
(9)

Evaluating x from the first equation and z from the third equation of Eq. (9), yields

$$\begin{aligned} \begin{array}{ll} x^{*}=\frac{\chi \gamma y^{*}+\varLambda }{\beta y^{*}+\mu +\psi },\qquad z^{*}=\frac{(1-\chi ) \gamma y^{*}+\psi x^{*}}{\beta \delta y^{*}+\mu }. \end{array} \end{aligned}$$
(10)

Substituting Eq. (10) in the second equation of Eq. (9) yields a quadratic equation in y as

$$\begin{aligned}{} & {} \beta \left( \chi \gamma y+\varLambda \right) \left( \beta \delta y+\mu \right) +\beta \delta y{\gamma }\left( 1-\chi \right) \nonumber \\ {}{} & {} \left( \beta y+\mu +\psi \right) +\beta \nonumber \\ {}{} & {} \delta \psi \left( \chi \gamma y+\varLambda \right) =(\mu +\gamma )\nonumber \\ {}{} & {} (\beta \delta y+\mu )(\beta y+\mu +\psi ). \qquad \end{aligned}$$
(11)

3.2.1 Perfect vaccination (\(\delta =0\))

In this case of perfect vaccination (\(\delta =0\)), Eq. (9) has a unique solution. The equilibrium points in this case are as follows.

$$\begin{aligned} \begin{array}{ll} x^{*}&{}=\frac{\varLambda \left( \left( \mu +\gamma \right) R_{\psi _{p}}-\chi \gamma \right) }{R_{\psi _{p}} \left( \left( 1-\chi \right) \gamma +\mu +\varLambda \beta \right) \left( \mu +\psi \right) -\varLambda \beta },\\ y^{*}&{}=\frac{\varLambda \left( R_{\psi _{p}}-1\right) }{R_{\psi _{p}}\left( \left( 1-\chi \right) \gamma +\mu \right) },\qquad z^{*}=\frac{(1-\chi ) \gamma y^{*}+\psi x^{*}}{\beta \delta y^{*}+\mu }. \end{array} \end{aligned}$$
(12)

The corresponding Jacobian matrix computed at \(E^{*}=(x^{*},y^{*},z^{*})\) is given by

$$\begin{aligned} J(E^{*})=\left( \begin{array}{ccc} a_{11} &{} a_{12} &{} 0 \\ \beta y^{*} &{} a_{22} &{} \beta \delta y^{*} \\ \psi &{} a_{32} &{} a_{33} \\ \end{array} \right) , \end{aligned}$$
(13)

with

$$\begin{aligned}\begin{array}{ll} a_{11}&{}=-\beta y^{*} -(\mu +\psi ),\\ a_{12}&{}=-\beta x^{*}+\chi \gamma ,\\ a_{22}&{}=\beta x^{*}+\beta \delta z^{*}-(\mu +\gamma ),\\ a_{32}&{}=-\beta \delta z^{*}+(1-\chi )\gamma , \\ a_{33}&{}=-\beta \delta y^{*}-\mu . \end{array} \end{aligned}$$

The system is stable if the roots of the characteristic polynomial (\(\mid J(E^{*})-\lambda I\mid =0\)) are all negative. It can be noticed from the reproduction number (\(R_{\psi _{p}}\)) of perfect vaccination that if the vaccination rate (\(\psi \)) is very high, the endemic equilibrium transfers into a disease-free equilibrium.

Fig. 3
figure 3

Response of the system approaching a disease-free equilibrium situation under perfect vaccination for \(R(\psi _{p})=0.0341\), \(\mu =3.93\times 10^{-06}\), \(\gamma =0.2\), \(\chi =0.8\), \(\psi =0.0017\), \(\delta =0\), \(\beta _{0}=1.6286\), \(\beta _{1}=0.8143\), \(T=360\), \(\phi =2.4435\)

Full size image

A situation approaching a disease-free equilibrium for the case of perfect vaccination and for the parameters \(\psi =0.0017\), \(\mu =3.93\times 10^{-06}\), \(\gamma =0.2\), \(\chi =0.8\), \(\delta =0\), \(\beta _{0}=1.6286\), \(\beta _{1}=0.8143\), \(T=360\), \(\phi =2.4435\) and \(R(\psi _{p})=0.0341\) is depicted in Fig. 3. This case demonstrates that for considerably high vaccination rate and if the vaccination is perfect, the situation approaches a disease-free equilibrium in which case we would be eradicating the disease completely.

3.2.2 Imperfect vaccination (\(\delta \ne 0\))

In this case of imperfect vaccination (\(\delta \ne 0\)), we investigate the equilibrium solution of Eq. (11). We rewrite Eq. (11) as follows.

$$\begin{aligned}{} & {} ay^2+by+c=0, \end{aligned}$$
(14)

with

$$\begin{aligned} a= & {} \beta ^{2} \delta \mu ,\\ b= & {} \beta ^{2} \delta \varLambda +\left( \chi \delta \gamma \mu -\chi \gamma \mu +\delta \,\mu ^{2}+\delta \mu \psi +\gamma \mu +\mu ^{2}\right) \beta ,\\ c= & {} \left( -\delta \varLambda \psi -\mu ^{2}\right) \beta +\gamma \,\mu ^{2}+\gamma \mu \psi +\mu ^{3}+\mu ^{2} \psi . \end{aligned}$$

We eliminate \(\beta \) from the coefficients of Eq. (14) by substituting \(\beta =\eta R(\psi )\). The resulting coefficients as a function of \(R(\psi )\) are

$$\begin{aligned} a= & {} R(\psi )^{2} \eta ^{2} \delta \mu , \nonumber \\ b= & {} -R(\psi )^{2} \eta ^{2} \delta \varLambda +((\chi \gamma +\mu +\psi ) \delta +(1-\chi ) \gamma \nonumber \\+ & {} \mu ) \mu R(\psi )\eta ,\nonumber \\ c= & {} (\delta \psi \varLambda +\mu ^2) R(\psi ) \eta +(\gamma +\psi +\mu ) \mu ^{2}+\gamma \mu \psi , \nonumber \\ \end{aligned}$$
(15)

where, \(\eta =\frac{\mu \left( \mu +\gamma \right) \left( \mu +\psi \right) }{\varLambda \left( \mu +\delta \psi \right) }\).

Fig. 4
figure 4

Saddle-node bifurcation showing infected versus reproduction number (\(R(\psi )\)) for the case of imperfect vaccination. In this case \(\delta =0.1\), \(\mu =0.0014\), \(\gamma =0.2\), \(\chi =0.8\). SN indicates the saddle-node bifurcation point. Stable solutions: blue lines, unstable solutions: red lines

Full size image

We solve Eq. (14) using coefficients given in Eq. (15) and plot the equilibrium values versus the reproduction number \(R(\psi )\) in Fig. 4, which displays typical saddle-node bifurcation behavior. The figure shows infected versus reproduction number for parameters \(\delta =0.1\), \(\mu =0.0014\), \(\gamma =0.2\), \(\chi =0.8\) and for different vaccination rates of \(\psi =\) 0.3, 0.64 and 0.9. It can be noticed from Fig. 4 that under imperfect vaccination, \(R(\psi )\) decreases until the saddle-node point and increases after that point with an increase in infections. Therefore, under imperfect vaccination, the stable disease-free equilibrium (blue lines in Fig. 4) transfers into an unstable endemic equilibrium (red lines in Fig. 4). This phenomenon is called backward bifurcation and occurs under imperfect vaccination. The fundamental cause for backward bifurcation is the fact that imperfect vaccination creates two classes of susceptible individuals with varying susceptibilities: the naive susceptible and the vaccinated susceptible [13]. Practically speaking, this means that if we vaccinate with a less effective vaccine, controlling the disease becomes more difficult due to the presence of backward bifurcation. We postulate that this is one of the main reasons for the dynamic oscillatory behavior of the COVID-19 epidemic.

Fig. 5
figure 5

Response of the system under imperfect vaccination for \(\mu =3.93\times 10^{-06}\), \(\gamma =0.2\), \(\chi =0.8\), \(\psi =0.0017\), \(\beta _{0}=1.6286\), \(\beta _{1}=0.8143\), \(T=360\), \(\phi =2.4435\). a \(\delta =0.1\), \(R(\psi )=1.5\) b \(\delta =0.5\), \(R(\psi )=7.4\)

Full size image

Figure 5 illustrates two different situations of imperfect vaccination (a) \(\delta =0.1\) and (b) \(\delta =0.5\) and for the parameters \(\mu =3.93\times 10^{-06}\), \(\gamma =0.2\), \(\chi =0.8\), \(\psi =0.0017\), \(\beta _{0}=1.6286\), \(\beta _{1}=0.8143\), \(T=360\), \(\phi =2.4435\). It can be noticed from Fig. 5 that imperfect vaccination leads to an endemic equilibrium ((a)\(R(\psi )=1.5\) and (b) \(R(\psi )=7.4\)) which is one of the causes for the dynamic behavior. It is also observed that with the increase in \(\delta \) from 0.1 to 0.5 the population of infected and susceptible classes increases due to backward bifurcation. Therefore, under imperfect vaccination, the eradication of disease becomes a very hard task since the endemic will persist for a very long time.

In the previous sections, we investigated the effect of vaccination on the dynamic behavior of the disease. In the following sections, the effect of other factors namely, the frequency at which the disease transmits and the amplitude of transmission rate is investigated.

3.3 Frequency and phase of transmission rate

The frequency at which the disease is transmitted is reflected in the time period for which the disease persists as depicted in Fig. 6 for (a) \(\varOmega =0.0349\) (\(T=180\)), \(\phi =2.09\) (b) \(\varOmega =0.0175\) (\(T=360\)), \(\phi =2.4435\) and for the parameters \(\mu =3.93\times 10^{-06}\), \(\gamma =0.2\), \(\chi =0.8\), \(\psi =0.0017\), \(\beta _{0}=1.6286\), \(\beta _{1}=0.8143\), \(\delta =0.1\). It is observed that when the frequency at which the disease transmits is more, the phase decreases and also the bandwidth of the peaks decreases as seen in Fig. 6a. On the other hand, with the decrease in transmission frequency, the phase and the bandwidth increase as shown in Fig. 6b. The phase here represents the transformation of the disease from the static to dynamic mode; the higher the phase, the longer it takes to transform from static to dynamic mode and vice versa. The bandwidth indicates the persistence of the disease for that time period; higher bandwidth indicates longer disease persistence.

Fig. 6
figure 6

Response of the system for \(\mu =3.93\times 10^{-06}\), \(\gamma =0.2\), \(\chi =0.8\), \(\psi =0.0017\), \(\beta _{0}=1.6286\), \(\beta _{1}=0.8143\), \(\delta =0.1\) a \(\varOmega =0.0349\) (\(T=180\)), \(\phi =2.09\) b \(\varOmega =0.0175\) (\(T=360\)), \(\phi =2.4435\)

Full size image

3.4 Amplitude of the transmission rate

The amplitude of the transmission rate plays a very important role in the spread of the pandemic. Figure 7 shows two situations for (a) \(\beta _{0}=1.6286\), \(\beta _{1}=0.8143\), \(R(\psi )=1.5\) (b) \(\beta _{0}=2.4428\), \(\beta _{1}=0.8143\), \(R(\psi )=2.26\) and for the parameters \(\mu =3.93\times 10^{-06}\), \(\gamma =0.2\), \(\chi =0.8\), \(\psi =0.0017\), \(\delta =0.1\), \(T=360\), \(\phi =2.4435\). It is evident from Fig. 7 that with the increase in amplitude of the transmission rate the peak of the infected population increases and so does the reproduction number (\(R(\psi )\)).

Fig. 7
figure 7

Response of the system for \(\mu =3.93\times 10^{-06}\), \(\gamma =0.2\), \(\chi =0.8\), \(\psi =0.0017\), \(\delta =0.1\), \(T=360\), \(\phi =2.4435\). a \(\beta _{0}=1.6286\), \(\beta _{1}=0.8143\), \(R(\psi )=1.5\) b \(\beta _{0}=2.4428\), \(\beta _{1}=0.8143\), \(R(\psi )=2.26\)

Full size image
Fig. 8
figure 8

Infection peak versus dynamic transmission rate (\(\beta _{0} \beta _{1}\)) for a constant vaccine reduction coefficient \(\delta =0.1\) b constant vaccination rate \(\psi =0.0017\) and for the parameters \(\mu =3.93\times 10^{-06}\), \(\gamma =0.2\), \(\chi =0.8\), \(T=180\), \(\phi =2.09\)

Full size image

Figure 8 shows the variation of the peak of the infected population versus dynamic transmission rate (\(\beta _{0}\beta _{1}\)) for (a) constant vaccine reduction coefficient \(\delta =0.1\) (b) constant vaccination rate \(\psi =0.0017\) and for the parameters \(\mu =3.93\times 10^{-06}\), \(\gamma =0.2\), \(\chi =0.8\), \(T=180\), \(\phi =2.09\). It is observed from Fig. 8a and b that with the increase in \(\beta _{0}\beta _{1}\) there is a sharp rise in the peak of the infected population until a certain value of \(\beta _{0}\beta _{1}\). After that, the peak of the infected population saturates.

The sharp rise of the peak is likely attributable to many reasons including delays in identifying and reporting cases, overlap of variants like delta and omicron, and ability of the variant to evade immunity conferred by past infection or vaccination (i.e., immune evasion). The lack of hospital bed capacity, as well as the weather circumstances at different times depending on the area, all contribute to the increase in the peak. Some other factors include bigger population sizes and border closures in highly infected urban areas, and sudden spread of infection from urban to rural areas. It follows that reduction of the static and dynamic transmission rates achieved through public health measures like wearing face masks, limiting public gatherings, more rigorous testing, and boosting vaccination efforts would clearly help to flatten the peaks of the infected population.

4 Summary of findings

We summarize below the key findings of our analysis.

  • In this paper, we defined a modified reproduction number for the Susceptible-Infected-Immune (SII) model in terms of \(\beta ,\mu \), \(\varLambda \), \(\gamma \), \(\psi \) and \(\delta \). This definition embeds the importance of vaccination seamlessly into the epidemiological model and significantly expands insight for controlling the disease.

  • There exists a critical minimum vaccination level for complete eradication of the disease.

  • The first harmonic approximation of transmission rate incorporated in the model explains the dynamic behavior of the disease adequately.

  • Imperfections in vaccination have a high impact on the persistence of the disease.

  • The persistence of the disease also depends on the frequency and phase of the transmission rate.

  • The peak values of the infected population depend on the frequency, phase and amplitude of the transmission rate. Analysis of these effects on peak values significantly expands the insight into the severity of the pandemic.

  • The model predicts that the peak of the infected population saturates more quickly if the population is vaccinated with near perfect vaccine even when the transmission rate increases constantly.

  • As we know, public health measures and governmental actions would reduce the transmission rate (something we did not model in this paper but has been widely documented). Hence, it follows that our analysis leads to the conclusion that a suitable combination of vaccination, public behavior and governmental actions would reduce the oscillations and hence, effectively and completely stop a pandemic such as COVID-19.

5 Conclusion

In this paper, we adapted and developed a Susceptible-Infected-Immune model for the COVID-19 pandemic including vaccination and a harmonic transmission rate. First, we used available data from the USA as base parameters. The numerical analysis is performed using the base parameters to explain the dynamic behavior of the disease and its control through vaccination.

Equilibrium and stability analysis were performed revealing several situations for disease-free equilibrium and endemic equilibrium under perfect and imperfect vaccination. The effect of frequency, phase, and amplitude of the transmission rate on the dynamic behavior of the disease is investigated.

We are able to show the fact that imperfect vaccination leads to a saddle-node bifurcation where the stable disease-free equilibrium transfers into an unstable endemic equilibrium. This phenomenon is called backward bifurcation and occurs under imperfect vaccination. The main reason is the fact that imperfect vaccination creates two subclasses of susceptible individuals with different susceptibilities: the naive susceptible and the vaccinated susceptible. The resulting backward bifurcation lends support to our argument that the practical task of combating COVID-19 becomes much harder if the vaccination is imperfect. This is one of the principal reasons for the persistent dynamic behavior of the COVID-19 epidemic.

The paper also demonstrated that the frequency, phase and amplitude of the transmission rate greatly affect the dynamic behavior of the disease. The persistence of the disease depends on the frequency and phase of transmission rate, while the peak of the infected population depends on the amplitude of the transmission rate. These findings confirm that the dynamic behavior of an endemic disease such as COVID-19 is driven by variables such as imperfect vaccination, environmental factors, and new variants of the virus. Social and biological elements, such as population density, social distancing measures, and government initiatives also have a role in the dynamic behavior of the disease.

Finally and importantly, our analysis suggests that increasing the number of vaccinations, improving the effectiveness of vaccination, and implementing public measures that reduce static and dynamic transmission rates would suppress oscillatory behavior and help to eradicate the disease completely.