Skip to main content
Springer Nature Link
Log in

Generalized model for steady-state bifurcations without parameters in memristor-based oscillators with lines of equilibria

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

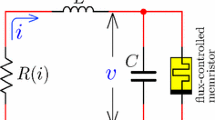
Abstract

We demonstrate how the pitchfork, transcritical and saddle-node bifurcations of steady states observed in dynamical systems with a finite number of isolated equilibrium points occur in systems with lines of equilibria. The exploration is carried out by using the numerical simulation and linear stability analysis applied to a model of a memristor-based circuit. All the discussed bifurcation scenarios are considered in the context of models with the piecewise-smooth memristor current-voltage characteristic (Chua’s memristor), as well as on examples of oscillators with the memristor nonlinearity that is smooth everywhere. Finally, we compare the dynamics of ideal-memristor-based oscillators with the behavior of models taking into account the memristor forgetting effect. The presented results are obtained for electronic circuit models, but the studied bifurcation phenomena can be exhibited by systems with lines of equilibria of any nature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Notes

  1. Here, we mean the direction being parallel to the OZ axis.

References

  1. Ascoli, A., Senger, V., Tetzlaff, R.: Memristor model comparison. IEEE Circuits Syst. Mag. 13(2), 89–105 (2013)

    Article  Google Scholar 

  2. Botta, V., Néspoli, C., Messias, M.: Mathematical analysis of a third-order memristor-based Chua’s oscillator. TEMA Tend. Mat. Apl. Comput. 12(2), 91–99 (2011)

    MathSciNet  MATH  Google Scholar 

  3. Chang, T., Jo, S., Kim, K., Sheridan, P., Gaba, S., Lu, W.: Synaptic behaviors and modeling of a metal oxide memristive device. Appl. Phys. A 102(4), 857–863 (2011)

    Article  Google Scholar 

  4. Chen, L., Li, C., Huang, T., Chen, Y., Wen, S., Qi, J.: A synapse memristor model with forgetting effect. Phys. Lett. A 377(45–48), 3260–3265 (2013)

    Article  Google Scholar 

  5. Chua, L.: Memristor-the missing circuit element. IEEE Trans. Circuit Theory CT–18(5), 507–519 (1971)

    Article  Google Scholar 

  6. Chua, L.: Resistance switching memories are memristors. Appl. Phys. A 102(4), 765–783 (2011)

    Article  MATH  Google Scholar 

  7. Chua, L., Kang, S.: Memristive devices and systems. Proc. IEEE 64(2), 209–223 (1976)

    Article  MathSciNet  Google Scholar 

  8. Corinto, F., Forti, M., Chua, L.: Nonlinear Circuits and Systems with Memristors. Springer, New York (2020)

    MATH  Google Scholar 

  9. Fiedler, B., Liebscher, S.: Hopf bifurcation from lines of equilibria without parameters: ii. Systems of viscous hyperbolic balance laws. SIAM J. Math. Anal. 31(6), 1396–1404 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  10. Fiedler, B., Liebscher, S., Alexander, J.: Generic Hopf bifurcation from lines of equilibria without parameters: I. Theory. J. Differ. Equ. 167(1), 16–35 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  11. Fiedler, B., Liebscher, S., Alexander, J.: Generic Hopf bifurcation from lines of equilibria without parameters: iii. Binary oscillators. Int. J. Bifurc. Chaos 10(7), 1613–1621 (2000)

    Article  MATH  Google Scholar 

  12. Gotthans, T., Petržela, J.: New class of chaotic systems with circular equilibrium. Nonlinear Dyn. 81(3), 1143–1149 (2015)

    Article  MathSciNet  Google Scholar 

  13. Gotthans, T., Sprott, J., Petrzela, J.: Simple chaotic flow with circle and square equilibrium. Int. J. Bifurc. Chaos 26(8), 1650,137 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  14. Guseinov, D., Matyushkin, I., Chernyaev, N., Mikhailov, A., Pershin, Y.: Capacitive effects can make memristors chaotic. Chaos Solitons Fractals 144, 110,699 (2021)

    Article  MathSciNet  Google Scholar 

  15. Itoh, M., Chua, L.: Memristor oscillators. Int. J. Bifurc Chaos 18(11), 3183–3206 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  16. Jafari, S., Sprott, J., Pham, V.T., Volos, C., Li, C.: Simple chaotic 3d flows with surfaces of equilibria. Nonlinear Dyn. 86(2), 1349–1358 (2016)

    Article  Google Scholar 

  17. Korneev, I., Semenov, V.: Andronov-Hopf bifurcation with and without parameter in a cubic memristor oscillator with a line of equilibria. Chaos 27(8), 081,104 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  18. Korneev, I., Semenov, V., Slepnev, A., Vadivasova, T.: Complete synchronization of chaos in systems with nonlinear inertial coupling. Chaos Solitons Fractals 142, 110,459 (2021)

    Article  MathSciNet  Google Scholar 

  19. Korneev, I., Slepnev, A., Vadivasova, T., Semenov, V.: Forced synchronization of an oscillator with a line of equilibria. Eur. Phys. J. Spec. Top. 229(12), 2215–2224 (2020)

    Article  Google Scholar 

  20. Korneev, I., Slepnev, A., Vadivasova, T., Semenov, V.: Subcritical Andronov-Hopf scenario for systems with a line of equilibria. Chaos 31(7), 073,102 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  21. Korneev, I., Vadivasova, T., Semenov, V.: Hard and soft excitation of oscillations in memristor-based oscillators with a line of equilibria. Nonlinear Dyn. 89(4), 2829–2843 (2017)

    Article  MathSciNet  Google Scholar 

  22. Liebscher, S.: Bifurcation without Parameters. Lectures Notes in Mathematics, vol. 2117. Springer, New York (2015)

  23. Linn, E., Siemon, A., Waser, R., Menzel, S.: Applicability of well-established memristive models for simulations of resistive switching devices. IEEE Trans. Circuits Syst. I Regul. Pap. 61(8), 2402–2410 (2014)

    Article  Google Scholar 

  24. Messias, M., Nespoli, C., Botta, V.: Hopf bifurcation from lines of equilibria without parameters in memristor oscillators. Int. J. Bifurc. Chaos 20(2), 437–450 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  25. Riaza, R.: Manifolds of equilibria and bifurcations without parameters in memristive circuits. SIAM J. Appl. Math. 72(3), 877–896 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  26. Riaza, R.: Transcritical bifurcation without parameters in memristive circuits. SIAM J. Appl. Math. 78(1), 395–417 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  27. Semenov, V.: Synthesis of memristive one-port circuits with piecewise-smooth characteristics. ArXiv: 2203.12708 (2022)

  28. Semenov, V., Korneev, I., Arinushkin, P., Strelkova, G., Vadivasova, T., Anishchenko, V.: Numerical and experimental studies of attractors in memristor-based Chua’s oscillator with a line of equilibria. Noise-induced effects. Eur. Phys. J. Spec. Top. 224(8), 1553–1561 (2015)

    Article  Google Scholar 

  29. Singh, J., Raj, B.: An accurate and generic window function for nonlinear memristor models. J. Comput. Electron. 18(2), 640–647 (2019)

    Article  MathSciNet  Google Scholar 

  30. Tetzlaff, R. (ed.): Memristor and Memristive Systems. Springer-Verlag, New York (2014)

    Google Scholar 

  31. Zhou, E., Fang, L., Yang, B.: A general method to describe forgetting effect of memristors. Phys. Lett. A 383(11), 942–948 (2019)

    Article  Google Scholar 

Download references

Acknowledgements

V.V.S. and A.S.Z. acknowledge support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Projektnummer—163436311-SFB-910. V.V.S. also acknowledges support by the Russian Science Foundation (Project No. 22-72-00038).

Author information

Authors and Affiliations

  1. Saratov State University, Astrakhanskaya str. 83, Saratov, Russia, 410012

    lvan A. Korneev, Andrei V. Slepnev, Tatiana E. Vadivasova & Vladimir V. Semenov

  2. Technische Universität Berlin, Hardenbergstraße 36, 10623, Berlin, Germany

    Anna S. Zakharova & Vladimir V. Semenov

Authors
  1. lvan A. Korneev
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Andrei V. Slepnev
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Anna S. Zakharova
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Tatiana E. Vadivasova
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Vladimir V. Semenov
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Vladimir V. Semenov.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Korneev, l.A., Slepnev, A.V., Zakharova, A.S. et al. Generalized model for steady-state bifurcations without parameters in memristor-based oscillators with lines of equilibria. Nonlinear Dyn 111, 1235–1243 (2023). https://doi.org/10.1007/s11071-022-07905-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-022-07905-6

Keywords