Nonlinear dynamics for a class of 2-DOF systems with viscoelastic limit devices on a curved track

Abstract

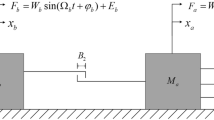
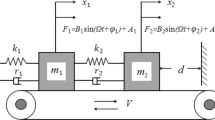
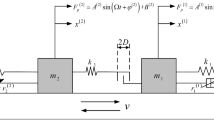
This paper presents the nonlinear dynamics of a complex 2-DOF (two degree-of-freedom) system including nonlinear stiffness and damping elements, friction as well as impact, and the purpose of study is to give an original and deep investigation on the discontinuous dynamical behaviors for such a 2-DOF system through strict mathematical consideration. Firstly, the physical model of the system consisting of a ball and an object with curved track and viscoelastic limit devices is established by Coulomb friction and non-linear spring-damping model. And the eight motion states associated with free, sliding or stick motions are defined for the oscillator. Secondly, based on the non-smoothness/discontinuity resulted from impact/friction, the phase space is divided into different domains and boundaries in absolute and relative coordinates, respectively. Thirdly, some necessary and sufficient conditions for oscillator’s motion switching at separation boundaries are given by G-functions of the flow switchability theory in discontinuous dynamical systems. Finally, in order to better understand the switching criteria and the complexity of oscillator’s motion, some illustrative examples for several typical motions in system are studied by numerical simulation. The nonlinear spring-damping model is widely used as a shock absorber in machinery, aerospace, construction and other fields, which can accurately reflect the energy loss during impact process.

Appendices

Appendix A

The phase spaces of $m _1$ and $m _2$ are divided in absolute coordinates, and the domains and boundaries are expressed in Eqs. (A.1-A.4) and Eqs. (A.5-A.8) according to whether stick motion occurs.

Without stick motion, the domains and boundaries of $m _{1}$ are expressed by

$$\begin{aligned}&\left\{ \begin{array}{lll} \text{\O}mega _{1}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;x _{1}\in (x _{2}-d ,\,x _{2}+d ),\;\dot{x }_{1}\in (\dot{x }_{2},+\infty )\cap (v ,+\infty )\},\\ \text{\O}mega _{2}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;x _{1}\in (x _{2}-d ,\,x _{2}+d ),\;\dot{x }_{1}\in (\dot{x }_{2},+\infty )\cap (-\infty ,\,v )\},\\ \text{\O}mega _{3}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;x _{1}\in (x _{2}-d ,\,x _{2}+d ),\;\dot{x }_{1}\in (-\infty ,\,\dot{x }_{2})\cap (v ,+\infty )\},\\ \text{\O}mega _{4}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;x _{1}\in (x _{2}-d ,\,x _{2}+d ),\;\dot{x }_{1}\in (-\infty ,\,\dot{x }_{2})\cap (-\infty ,\,v )\};\\ \end{array}\right. \qquad \qquad \qquad \qquad \end{aligned}$$

(A.1)

$$\begin{aligned}&\left\{ \begin{array}{lll} \partial \text{\O}mega _{12}^{(1)}=\partial \text{\O}mega _{21}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{12}^{(1)}=\varphi _{21}^{(1)}\equiv \dot{x }_{1}-v =0,\;\dot{x }_{1}\in (\dot{x }_{2},+\infty ),\;x _{1}\in (x _{2}-d ,\,x _{2}+d )\bigr \},\\ \partial \text{\O}mega _{34}^{(1)}=\partial \text{\O}mega _{43}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{34}^{(1)}=\varphi _{43}^{(1)}\equiv \dot{x }_{1}-v =0,\;\dot{x }_{1}\in (-\infty ,\dot{x }_{2}),\;x _{1}\in (x _{2}-d ,\,x _{2}+d )\bigr \},\\ \partial \text{\O}mega _{13}^{(1)}=\partial \text{\O}mega _{31}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{13}^{(1)}=\varphi _{31}^{(1)}\equiv \dot{x }_{1}-\dot{x }_{2}=0,\;\dot{x }_{1}\in (v ,+\infty ),\;x _{1}\in (x _{2}-d ,\,x _{2}+d )\bigr \},\\ \partial \text{\O}mega _{24}^{(1)}=\partial \text{\O}mega _{42}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{24}^{(1)}=\varphi _{42}^{(1)}\equiv \dot{x }_{1}-\dot{x }_{2}=0,\;\dot{x }_{1}\in (-\infty ,v ),\;x _{1}\in (x _{2}-d ,\,x _{2}+d )\bigr \},\\ ^1\partial \text{\O}mega _{1\infty }^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;^1\varphi _{1\infty }^{(1)}\equiv x _{1}-x _{2}-d =0,\;\dot{x }_{1}>\dot{x }_{2}\},\\ ^1\partial \text{\O}mega _{4\infty }^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;^1\varphi _{4\infty }^{(1)}\equiv x _{1}-x _{2}-d =0,\;\dot{x }_{1}<\dot{x }_{2}\},\\ ^2\partial \text{\O}mega _{1\infty }^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;^2\varphi _{1\infty }^{(1)}\equiv x _{1}-x _{2}+d =0,\;\dot{x }_{1}>\dot{x }_{2}\},\\ ^2\partial \text{\O}mega _{4\infty }^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;^2\varphi _{4\infty }^{(1)}\equiv x _{1}-x _{2}+d =0,\;\dot{x }_{1}<\dot{x }_{2}\},\\ \end{array}\right. \qquad \qquad \qquad \nonumber \\ \end{aligned}$$

(A.2)

and the domains and boundaries of $m _{2}$ are expressed by

$$\begin{aligned}&\left\{ \begin{array}{lll} \text{\O}mega _{1}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\; |\;x _{2}\in (x _{1}-d ,\,x _{1}+{} d ),\;\dot{x }_{2}\in (-\infty ,\dot{x }_{1})\},\\ \text{\O}mega _{2}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\; |\;x _{2}\in (x _{1}-d ,\,x _{1}+d ),\;\dot{x }_{2}\in (\dot{x }_{1},+\infty )\}; \end{array}\right. \end{aligned}$$

(A.3)

$$\begin{aligned}&\left\{ \begin{array}{lll} \partial \text{\O}mega _{12}^{(2)}=\partial \text{\O}mega _{21}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\;|\;\varphi _{12}^{(2)}=\varphi _{21}^{(2)}\equiv \dot{x }_{2}-\dot{x }_{1}=0,\\ \qquad \qquad \qquad \qquad \qquad \;x _{2}\in (x _{1}-d ,\,x _{1}+d )\bigr \},\\ ^1\partial \text{\O}mega _{1\infty }^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\;|\;^1\varphi _{1\infty }^{(2)}\equiv x _{2}-x _{1}+d =0,\;\dot{x }_{2}<\dot{x }_{1}\},\\ ^1\partial \text{\O}mega _{2\infty }^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\;|\;^1\varphi _{2\infty }^{(2)}\equiv x _{2}-x _{1}+d =0,\;\dot{x }_{2}>\dot{x }_{1}\},\\ ^2\partial \text{\O}mega _{1\infty }^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\;|\;^2\varphi _{1\infty }^{(2)}\equiv x _{2}-x _{1}-d =0,\;\dot{x }_{2}<\dot{x }_{1}\},\\ ^2\partial \text{\O}mega _{2\infty }^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\;|\;^2\varphi _{2\infty }^{(2)}\equiv x _{2}-x _{1}-d =0,\;\dot{x }_{2}>\dot{x }_{1}\}. \end{array}\right. \nonumber \\ \end{aligned}$$

(A.4)

Fig. 23

Absolute domains and boundaries without stick motion for the two masses: a object $m _1$ and b ball $m _2$

As shown in Fig. 23, the domains $\text{\O}mega _{\lambda }^{(1)}$ $(\lambda =1,2,3,4)$ are expressed in violet, pink, salmon and orange, respectively, where the object $m _1$ is in free motion without stick. The domains where the ball $m _2$ does free motion without stick are $\text{\O}mega _{1}^{(2)}$ and $\text{\O}mega _{2}^{(2)}$, which are expressed in pink and orange. The velocity boundaries $\partial \text{\O}mega _{12}^{(1)}$ and $\partial \text{\O}mega _{34}^{(1)}$ of the object $m _1$, which represent the speed of the conveyor belt, are painted as blue dotted lines. The velocity boundaries $\partial \text{\O}mega _{13}^{(1)}$ and $\partial \text{\O}mega _{24}^{(1)}$ of the object $m _1$, which represent the speed of the ball $m _2$, are expressed in the red dashed curves. The velocity boundary $\partial \text{\O}mega _{12}^{(2)}$ of the ball $m _2$ is also expressed in the red dashed curve. The impact boundaries $^1\partial \text{\O}mega _{\tau \infty }^{(i )}$ and $^2\partial \text{\O}mega _{\tau \infty }^{(i )}\,\,(\tau \in \{1,4\}\, \mathrm{if}\,i =1;\,\,\tau \in \{1,2\}\,\mathrm{if}\,i =2)$ are expressed in black dotted dashed curves. With stick motion, the domains and boundaries of $m _{1}$ are defined as

$$\begin{aligned}&\left\{ \begin{array}{lll} \text{\O}mega _{1}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;x _{1}\in (x _{2}-d ,\,x _{2}+d ),\;\dot{x }_{1}\in (\dot{x }_{2},+\infty )\cap (v ,+\infty )\},\\ \text{\O}mega _{2}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;x _{1}\in (x _{2}-d ,\,x _{2}+d ),\;\dot{x }_{1}\in (\dot{x }_{2},+\infty )\cap (-\infty ,\,v )\},\\ \text{\O}mega _{3}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;x _{1}\in (x _{2}-d ,\,x _{2}+d ),\;\dot{x }_{1}\in (-\infty ,\,\dot{x }_{2})\cap (v ,+\infty )\},\\ \text{\O}mega _{4}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;x _{1}\in (x _{2}-d ,\,x _{2}+d ),\;\dot{x }_{1}\in (-\infty ,\,\dot{x }_{2})\cap (-\infty ,\,v )\},\\ \text{\O}mega _{5}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;x _{1}\in (x _{2}+d ,\,+\infty ),\;\dot{x }_{1}\in (\dot{x }_{2},+\infty )\cap (v ,+\infty )\},\\ \text{\O}mega _{6}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;x _{1}\in (x _{2}+d ,\,+\infty ),\;\dot{x }_{1}\in (\dot{x }_{2},+\infty )\cap (-\infty ,\,v )\},\\ \text{\O}mega _{7}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;x _{1}\in (x _{2}+d ,\,+\infty ),\;\dot{x }_{1}\in (-\infty ,\,\dot{x }_{2})\cap (v ,+\infty )\},\\ \text{\O}mega _{8}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;x _{1}\in (x _{2}+d ,\,+\infty ),\;\dot{x }_{1}\in (-\infty ,\,\dot{x }_{2})\cap (-\infty ,\,v )\},\\ \text{\O}mega _{9}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;x _{1}\in (-\infty ,\,x _{2}-d ),\;\dot{x }_{1}\in (\dot{x }_{2},+\infty )\cap (v ,+\infty )\},\\ \text{\O}mega _{a}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;x _{1}\in (-\infty ,\,x _{2}-d ),\;\dot{x }_{1}\in (\dot{x }_{2},+\infty )\cap (-\infty ,\,v )\},\\ \text{\O}mega _{b}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;x _{1}\in (-\infty ,\,x _{2}-d ),\;\dot{x }_{1}\in (-\infty ,\,\dot{x }_{2})\cap (v ,+\infty )\},\\ \text{\O}mega _{c}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\; |\;x _{1}\in (-\infty ,\,x _{2}-d ),\;\dot{x }_{1}\in (-\infty ,\,\dot{x }_{2})\cap (-\infty ,\,v )\};\\ \end{array}\right. \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \end{aligned}$$

(A.5)

$$\begin{aligned}&\left\{ \begin{array}{lll} \partial \text{\O}mega _{12}^{(1)}=\partial \text{\O}mega _{21}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{12}^{(1)}=\varphi _{21}^{(1)}\equiv \dot{x }_{1}-v =0,\;\dot{x }_{1}\in (\dot{x }_{2},+\infty ),\;x _{1}\in (x _{2}-d ,\,x _{2}+d )\bigr \},\\ \partial \text{\O}mega _{34}^{(1)}=\partial \text{\O}mega _{43}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{34}^{(1)}=\varphi _{43}^{(1)}\equiv \dot{x }_{1}-v =0,\;\dot{x }_{1}\in (-\infty ,\dot{x }_{2}),\;x _{1}\in (x _{2}-d ,\,x _{2}+d )\bigr \},\\ \partial \text{\O}mega _{56}^{(1)}=\partial \text{\O}mega _{65}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{56}^{(1)}=\varphi _{65}^{(1)}\equiv \dot{x }_{1}-v =0,\;\dot{x }_{1}\in (\dot{x }_{2},+\infty ),\;x _{1}\in (x _{2}+d ,\,+\infty )\bigr \},\\ \partial \text{\O}mega _{78}^{(1)}=\partial \text{\O}mega _{87}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{78}^{(1)}=\varphi _{87}^{(1)}\equiv \dot{x }_{1}-v =0,\;\dot{x }_{1}\in (-\infty ,\dot{x }_{2}),\;x _{1}\in (x _{2}+d ,\,+\infty )\bigr \},\\ \partial \text{\O}mega _{9a}^{(1)}=\partial \text{\O}mega _{a9}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{9a}^{(1)}=\varphi _{a9}^{(1)}\equiv \dot{x }_{1}-v =0,\;\dot{x }_{1}\in (\dot{x }_{2},+\infty ),\;x _{1}\in (-\infty ,\,x _{2}-d )\bigr \},\\ \partial \text{\O}mega _{bc}^{(1)}=\partial \text{\O}mega _{cb}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{bc}^{(1)}=\varphi _{cb}^{(1)}\equiv \dot{x }_{1}-v =0,\;\dot{x }_{1}\in (-\infty ,\dot{x }_{2}),\;x _{1}\in (-\infty ,\,x _{2}-d )\bigr \},\\ \partial \text{\O}mega _{13}^{(1)}=\partial \text{\O}mega _{31}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{13}^{(1)}=\varphi _{31}^{(1)}\equiv \dot{x }_{1}-\dot{x }_{2}=0,\;\dot{x }_{1}\in (v ,+\infty ),\;x _{1}\in (x _{2}-d ,\,x _{2}+d )\bigr \},\\ \partial \text{\O}mega _{24}^{(1)}=\partial \text{\O}mega _{42}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{24}^{(1)}=\varphi _{42}^{(1)}\equiv \dot{x }_{1}-\dot{x }_{2}=0,\;\dot{x }_{1}\in (-\infty ,v ),\;x _{1}\in (x _{2}-d ,\,x _{2}+d )\bigr \},\\ \partial \text{\O}mega _{57}^{(1)}=\partial \text{\O}mega _{75}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{57}^{(1)}=\varphi _{75}^{(1)}\equiv \dot{x }_{1}-\dot{x }_{2}=0,\;\dot{x }_{1}\in (v ,+\infty ),\;x _{1}\in (x _{2}+d ,\,+\infty )\bigr \},\\ \partial \text{\O}mega _{68}^{(1)}=\partial \text{\O}mega _{86}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{68}^{(1)}=\varphi _{86}^{(1)}\equiv \dot{x }_{1}-\dot{x }_{2}=0,\;\dot{x }_{1}\in (-\infty ,v ),\;x _{1}\in (x _{2}+d ,\,+\infty )\bigr \},\\ \partial \text{\O}mega _{9b}^{(1)}=\partial \text{\O}mega _{b9}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{9b}^{(1)}=\varphi _{b9}^{(1)}\equiv \dot{x }_{1}-\dot{x }_{2}=0,\;\dot{x }_{1}\in (v ,+\infty ),\;x _{1}\in (-\infty ,\,x _{2}-d )\bigr \},\\ \partial \text{\O}mega _{ac}^{(1)}=\partial \text{\O}mega _{ca}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{ac}^{(1)}=\varphi _{ca}^{(1)}\equiv \dot{x }_{1}-\dot{x }_{2}=0,\;\dot{x }_{1}\in (-\infty ,v ),\;x _{1}\in (-\infty ,\,x _{2}-d )\bigr \},\\ \partial \text{\O}mega _{15}^{(1)}=\partial \text{\O}mega _{51}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{15}^{(1)}=\varphi _{51}^{(1)}\equiv x _{1}-x _{2}-d =0,\;\dot{x }_{1}>\dot{x }_{2}\},\\ \partial \text{\O}mega _{48}^{(1)}=\partial \text{\O}mega _{84}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{48}^{(1)}=\varphi _{84}^{(1)}\equiv x _{1}-x _{2}-d =0,\;\dot{x }_{1}<\dot{x }_{2}\},\\ \partial \text{\O}mega _{19}^{(1)}=\partial \text{\O}mega _{91}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{19}^{(1)}=\varphi _{91}^{(1)}\equiv x _{1}-x _{2}+d =0,\;\dot{x }_{1}>\dot{x }_{2}\},\\ \partial \text{\O}mega _{4c}^{(1)}=\partial \text{\O}mega _{c4}^{(1)}=\bigl \{(x _{1},\dot{x }_{1})\;|\;\varphi _{4c}^{(1)}=\varphi _{c4}^{(1)}\equiv x _{1}-x _{2}+d =0,\;\dot{x }_{1}<\dot{x }_{2}\}, \end{array}\right. \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \nonumber \\ \end{aligned}$$

(A.6)

and the domains and boundaries of $m _{2}$ are defined as

$$\begin{aligned}&\left\{ \begin{array}{lll} \text{\O}mega _{1}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\; |\;x _{2}\in (x _{1}-d ,\,x _{1}+d ),\;\dot{x }_{2}\in (-\infty ,\dot{x }_{1})\},\\ \text{\O}mega _{2}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\; |\;x _{2}\in (x _{1}-d ,\,x _{1}+d ),\;\dot{x }_{2}\in (\dot{x }_{1},+\infty )\},\\ \text{\O}mega _{3}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\; |\;x _{2}\in (-\infty ,\,x _{1}-d ),\;\dot{x }_{2}\in (-\infty ,\dot{x }_{1})\},\\ \text{\O}mega _{4}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\; |\;x _{2}\in (-\infty ,\,x _{1}-d ),\;\dot{x }_{2}\in (\dot{x }_{1},+\infty )\},\\ \text{\O}mega _{5}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\; |\;x _{2}\in (x _{1}+d ,\,+\infty ),\;\dot{x }_{2}\in (-\infty ,\dot{x }_{1})\},\\ \text{\O}mega _{6}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\; |\;x _{2}\in (x _{1}+d ,\,+\infty ),\;\dot{x }_{2}\in (\dot{x }_{1},+\infty )\}; \end{array}\right. \qquad \qquad \qquad \qquad \quad \qquad \qquad \quad \end{aligned}$$

(A.7)

$$\begin{aligned}&\left\{ \begin{array}{lll} \partial \text{\O}mega _{12}^{(2)}=\partial \text{\O}mega _{21}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\;|\;\varphi _{12}^{(2)}=\varphi _{21}^{(2)}\equiv \dot{x }_{2}-\dot{x }_{1}=0,\;x _{2}\in (x _{1}-d ,\,x _{1}+d )\bigr \},\\ \partial \text{\O}mega _{34}^{(2)}=\partial \text{\O}mega _{43}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\;|\;\varphi _{34}^{(2)}=\varphi _{43}^{(2)}\equiv \dot{x }_{2}-\dot{x }_{1}=0,\;x _{2}\in (-\infty ,\,x _{1}-d )\bigr \},\\ \partial \text{\O}mega _{56}^{(2)}=\partial \text{\O}mega _{65}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\;|\;\varphi _{56}^{(2)}=\varphi _{65}^{(2)}\equiv \dot{x }_{2}-\dot{x }_{1}=0,\;x _{2}\in (x _{1}+d ,\,+\infty )\bigr \},\\ \partial \text{\O}mega _{26}^{(2)}=\partial \text{\O}mega _{62}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\;|\;\varphi _{26}^{(2)}=\varphi _{62}^{(2)}\equiv x _{2}-x _{1}-d =0,\;\dot{x }_{2}>\dot{x }_{1}\},\\ \partial \text{\O}mega _{15}^{(2)}=\partial \text{\O}mega _{51}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\;|\;\varphi _{15}^{(2)}=\varphi _{51}^{(2)}\equiv x _{2}-x _{1}-d =0,\;\dot{x }_{2}<\dot{x }_{1}\},\\ \partial \text{\O}mega _{24}^{(2)}=\partial \text{\O}mega _{42}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\;|\;\varphi _{24}^{(2)}=\varphi _{42}^{(2)}\equiv x _{2}-x _{1}+d =0,\;\dot{x }_{2}>\dot{x }_{1}\},\\ \partial \text{\O}mega _{13}^{(2)}=\partial \text{\O}mega _{31}^{(2)}=\bigl \{(x _{2},\dot{x }_{2})\;|\;\varphi _{13}^{(2)}=\varphi _{31}^{(2)}\equiv x _{2}-x _{1}+d =0,\;\dot{x }_{2}<\dot{x }_{1}\}. \end{array}\right. \qquad \qquad \qquad \qquad \quad \qquad \qquad \quad \end{aligned}$$

(A.8)

Fig. 24

Absolute domains and boundaries with stick motion for the two masses: a object $m _1$ and b ball $m _2$

As shown in Fig. 24, the domains $\text{\O}mega _{\tau }^{(1)}$ $(\tau =5,6,7,8,9,a,b,c)$ are expressed in yellow, light yellow, light green, green, blue, light blue, light purple and purple, respectively, where the object $m _1$ is in free motion with stick. The domains $\text{\O}mega _{\tau }^{(2)}$ $(\tau =3,4,5,6)$ represent the domains where the ball $m _2$ does free motion with stick and are expressed in light yellow, light green, blue and purple, respectively. On the stick domains, the boundary $\partial \text{\O}mega _{\alpha \beta }^{(1)}$ $((\alpha , \beta )\in \{(5,6),(7,8),(9,a),(b,c)\})$ of the object $m _1$ related to the speed of the conveyor belt is shown by darkgreen dotted line, the boundary $\partial \text{\O}mega _{\alpha \beta }^{(1)}$ $((\alpha , \beta )\in \{(5,7),(6,8),(9,b),(a,c)\})$ of the object $m _1$ related to the speed of the ball $m _2$ is shown by gold dashed curve, and the velocity boundaries $\partial \text{\O}mega _{34}^{(2)}$ and $\partial \text{\O}mega _{56}^{(2)}$ of the ball $m _2$ are also shown by gold dashed curves. The displacement boundaries $\partial \text{\O}mega _{j {} n }^{(1)}$ and $\partial \text{\O}mega _{u g}^{(2)}\,\,((j ,n )\in \{(1,5),(1,9),(4,8),(4,c)\};\,\,(u ,g)\in \{(1,3),(1,5),(2,4),(2,6)\})$ are expressed in black dotted dashed curves.

Appendix B

In relative coordinates, the relative domains and boundaries of $m _1$ with stick motion are expressed by

$$\begin{aligned}&\left\{ \begin{array}{lll} \text{\O}mega _{1}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\; |\;z _{1}\in (-d ,\,d ),\;\dot{z }_{1}\in (0,+\infty )\cap (v -\dot{x }_{2},+\infty )\},\\ \text{\O}mega _{2}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\; |\;z _{1}\in (-d ,\,d ),\;\dot{z }_{1}\in (0,+\infty )\cap (-\infty ,\,v -\dot{x }_{2})\},\\ \text{\O}mega _{3}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\; |\;z _{1}\in (-d ,\,d ),\;\dot{z }_{1}\in (-\infty ,\,0)\cap (v -\dot{x }_{2},+\infty )\},\\ \text{\O}mega _{4}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\; |\;z _{1}\in (-d ,\,d ),\;\dot{z }_{1}\in (-\infty ,\,0)\cap (-\infty ,\,v -\dot{x }_{2})\},\\ \text{\O}mega _{5}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\; |\;z _{1}\in (d ,\,+\infty ),\;\dot{z }_{1}\in (0,+\infty )\cap (v -\dot{x }_{2},+\infty )\},\\ \text{\O}mega _{6}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\; |\;z _{1}\in (d ,\,+\infty ),\;\dot{z }_{1}\in (0,+\infty )\cap (-\infty ,\,v -\dot{x }_{2})\},\\ \text{\O}mega _{7}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\; |\;z _{1}\in (d ,\,+\infty ),\;\dot{z }_{1}\in (-\infty ,\,0)\cap (v -\dot{x }_{2},+\infty )\},\\ \text{\O}mega _{8}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\; |\;z _{1}\in (d ,\,+\infty ),\;\dot{z }_{1}\in (-\infty ,\,0)\cap (-\infty ,\,v -\dot{x }_{2})\},\\ \text{\O}mega _{9}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\; |\;z _{1}\in (-\infty ,\,-d ),\;\dot{z }_{1}\in (0,+\infty )\cap (v -\dot{x }_{2},+\infty )\},\\ \text{\O}mega _{a}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\; |\;z _{1}\in (-\infty ,\,-d ),\;\dot{z }_{1}\in (0,+\infty )\cap (-\infty ,\,v -\dot{x }_{2})\},\\ \text{\O}mega _{b}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\; |\;z _{1}\in (-\infty ,\,-d ),\;\dot{z }_{1}\in (-\infty ,\,0)\cap (v -\dot{x }_{2},+\infty )\},\\ \text{\O}mega _{c}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\; |\;z _{1}\in (-\infty ,\,-d ),\;\dot{z }_{1}\in (-\infty ,\,0)\cap (-\infty ,\,v -\dot{x }_{2})\};\\ \end{array}\right. \qquad \qquad \qquad \end{aligned}$$

(B.1)

$$\begin{aligned}&\left\{ \begin{array}{lll} \partial \text{\O}mega _{12}^{(1)}=\partial \text{\O}mega _{21}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\;|\;\varphi _{12}^{(1)}=\varphi _{21}^{(1)}\equiv \dot{z }_{1}-(v -\dot{x }_{2})=0,\;\dot{z }_{1}\in (0,+\infty ),\;z _{1}\in (-d ,\,d )\bigr \},\\ \partial \text{\O}mega _{34}^{(1)}=\partial \text{\O}mega _{43}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\;|\;\varphi _{34}^{(1)}=\varphi _{43}^{(1)}\equiv \dot{z }_{1}-(v -\dot{x }_{2})=0,\;\dot{z }_{1}\in (-\infty ,0),\;z _{1}\in (-d ,\,d )\bigr \},\\ \partial \text{\O}mega _{56}^{(1)}=\partial \text{\O}mega _{65}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\;|\;\varphi _{56}^{(1)}=\varphi _{65}^{(1)}\equiv \dot{z }_{1}-(v -\dot{x }_{2})=0,\;\dot{z }_{1}\in (0,+\infty ),\;z _{1}\in (d ,\,+\infty )\bigr \},\\ \partial \text{\O}mega _{78}^{(1)}=\partial \text{\O}mega _{87}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\;|\;\varphi _{78}^{(1)}=\varphi _{87}^{(1)}\equiv \dot{z }_{1}-(v -\dot{x }_{2})=0,\;\dot{z }_{1}\in (-\infty ,0),\;z _{1}\in (d ,\,+\infty )\bigr \},\\ \partial \text{\O}mega _{9a}^{(1)}=\partial \text{\O}mega _{a9}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\;|\;\varphi _{9a}^{(1)}=\varphi _{a9}^{(1)}\equiv \dot{z }_{1}-(v -\dot{x }_{2})=0,\;\dot{z }_{1}\in (0,+\infty ),\;z _{1}\in (-\infty ,\,-d )\bigr \},\\ \partial \text{\O}mega _{bc}^{(1)}=\partial \text{\O}mega _{cb}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\;|\;\varphi _{bc}^{(1)}=\varphi _{cb}^{(1)}\equiv \dot{z }_{1}-(v -\dot{x }_{2})=0,\;\dot{z }_{1}\in (-\infty ,0),\;z _{1}\in (-\infty ,\,-d )\bigr \},\\ \partial \text{\O}mega _{13}^{(1)}=\partial \text{\O}mega _{31}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\;|\;\varphi _{13}^{(1)}=\varphi _{31}^{(1)}\equiv \dot{z }_{1}=0,\;\dot{z }_{1}\in (v -\dot{x }_{2},+\infty ),\;z _{1}\in (-d ,\,d )\bigr \},\\ \partial \text{\O}mega _{24}^{(1)}=\partial \text{\O}mega _{42}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\;|\;\varphi _{24}^{(1)}=\varphi _{42}^{(1)}\equiv \dot{z }_{1}=0,\;\dot{z }_{1}\in (-\infty ,v -\dot{x }_{2}),\;z _{1}\in (-d ,\,d )\bigr \},\\ \partial \text{\O}mega _{57}^{(1)}=\partial \text{\O}mega _{75}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\;|\;\varphi _{57}^{(1)}=\varphi _{75}^{(1)}\equiv \dot{z }_{1}=0,\;\dot{z }_{1}\in (v -\dot{x }_{2},+\infty ),\;z _{1}\in (d ,\,+\infty )\bigr \},\\ \partial \text{\O}mega _{68}^{(1)}=\partial \text{\O}mega _{86}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\;|\;\varphi _{68}^{(1)}=\varphi _{86}^{(1)}\equiv \dot{z }_{1}=0,\;\dot{z }_{1}\in (-\infty ,v -\dot{x }_{2}),\;z _{1}\in (d ,\,+\infty )\bigr \},\\ \partial \text{\O}mega _{9b}^{(1)}=\partial \text{\O}mega _{b9}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\;|\;\varphi _{9b}^{(1)}=\varphi _{b9}^{(1)}\equiv \dot{z }_{1}=0,\;\dot{z }_{1}\in (v -\dot{x }_{2},+\infty ),\;z _{1}\in (-\infty ,\,-d )\bigr \},\\ \partial \text{\O}mega _{ac}^{(1)}=\partial \text{\O}mega _{ca}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\;|\;\varphi _{ac}^{(1)}=\varphi _{ca}^{(1)}\equiv \dot{z }_{1}=0,\;\dot{z }_{1}\in (-\infty ,v -\dot{x }_{2}),\;z _{1}\in (-\infty ,\,-d )\bigr \},\\ \partial \text{\O}mega _{15}^{(1)}=\partial \text{\O}mega _{51}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\;|\;\varphi _{15}^{(1)}=\varphi _{51}^{(1)}\equiv z _{1}-d =0,\;\dot{z }_{1}>0\},\\ \partial \text{\O}mega _{48}^{(1)}=\partial \text{\O}mega _{84}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\;|\;\varphi _{48}^{(1)}=\varphi _{84}^{(1)}\equiv z _{1}-d =0,\;\dot{z }_{1}<0\},\\ \partial \text{\O}mega _{19}^{(1)}=\partial \text{\O}mega _{91}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\;|\;\varphi _{19}^{(1)}=\varphi _{91}^{(1)}\equiv z _{1}+d =0,\;\dot{z }_{1}>0\},\\ \partial \text{\O}mega _{4c}^{(1)}=\partial \text{\O}mega _{c4}^{(1)}=\bigl \{(z _{1},\dot{z }_{1})\;|\;\varphi _{4c}^{(1)}=\varphi _{c4}^{(1)}\equiv z _{1}+d =0,\;\dot{z }_{1}<0\}, \end{array}\right. \qquad \qquad \qquad \end{aligned}$$

(B.2)

and the domains and boundaries of $m _{2}$ with stick motion are expressed by

$$\begin{aligned}&\left\{ \begin{array}{lll} \text{\O}mega _{1}^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\; |\;z _{2}\in (-d ,\,d ),\;\dot{z }_{2}\in (-\infty ,0)\},\\ \text{\O}mega _{2}^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\; |\;z _{2}\in (-d ,\,d ),\;\dot{z }_{2}\in (0,+\infty )\},\\ \text{\O}mega _{3}^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\; |\;z _{2}\in (-\infty ,\,-d ),\;\dot{z }_{2}\in (-\infty ,0)\},\\ \text{\O}mega _{4}^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\; |\;z _{2}\in (-\infty ,\,-d ),\;\dot{z }_{2}\in (0,+\infty )\},\\ \text{\O}mega _{5}^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\; |\;z _{2}\in (d ,\,+\infty ),\;\dot{z }_{2}\in (-\infty ,0)\},\\ \text{\O}mega _{6}^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\; |\;z _{2}\in (d ,\,+\infty ),\;\dot{z }_{2}\in (0,+\infty )\}; \end{array}\right. \end{aligned}$$

(B.3)

$$\begin{aligned}&\left\{ \begin{array}{lll} \partial \text{\O}mega _{12}^{(2)}=\partial \text{\O}mega _{21}^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\;|\;\varphi _{12}^{(2)}=\varphi _{21}^{(2)}\equiv \dot{z }_{2}=0,\;|z _{2}|<d \bigr \},\\ \partial \text{\O}mega _{34}^{(2)}=\partial \text{\O}mega _{43}^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\;|\;\varphi _{34}^{(2)}=\varphi _{43}^{(2)}\equiv \dot{z }_{2}=0,\;z _{2}<-d \bigr \},\\ \partial \text{\O}mega _{56}^{(2)}=\partial \text{\O}mega _{65}^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\;|\;\varphi _{56}^{(2)}=\varphi _{65}^{(2)}\equiv \dot{z }_{2}=0,\;z _{2}>d \bigr \},\\ \partial \text{\O}mega _{26}^{(2)}=\partial \text{\O}mega _{62}^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\;|\;\varphi _{26}^{(2)}=\varphi _{62}^{(2)}\equiv z _{2}-d =0,\;\dot{z }_{2}>0\bigr \},\\ \partial \text{\O}mega _{15}^{(2)}=\partial \text{\O}mega _{51}^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\;|\;\varphi _{15}^{(2)}=\varphi _{51}^{(2)}\equiv z _{2}-d =0,\;\dot{z }_{2}<0\bigr \},\\ \partial \text{\O}mega _{24}^{(2)}=\partial \text{\O}mega _{42}^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\;|\;\varphi _{24}^{(2)}=\varphi _{42}^{(2)}\equiv z _{2}+d =0,\;\dot{z }_{2}>0\bigr \},\\ \partial \text{\O}mega _{13}^{(2)}=\partial \text{\O}mega _{31}^{(2)}=\bigl \{(z _{2},\dot{z }_{2})\;|\;\varphi _{13}^{(2)}=\varphi _{31}^{(2)}\equiv z _{2}+d =0,\;\dot{z }_{2}<0\bigr \}. \end{array}\right. \nonumber \\ \end{aligned}$$

(B.4)

Fig. 25

Relative domains and boundaries with stick motion for the two masses: a object $m _1$ and b ball $m _2$

As shown in Fig. 25, the velocity boundaries related to the speed of the object $m _1$ or the ball $m _2$ become straight lines which are time-independent and are represented by red (without stick motion) or yellow (with stick motion), and the displacement boundaries become black straight lines which are time-independent.