Skip to main content
Springer Nature Link
Log in

Suppressing chaos in crystal growth process using adaptive phase resonant perturbation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

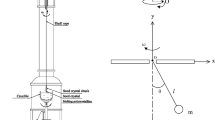
Chaos occurs in the flexible shaft rotating-lifting (FSRL) system of crystal growth process. Chaotic swing does harm to the quality of mono-silicon crystal production. Therefore, it must be suppressed. Previous studies have proposed impulse control method to suppress the chaos in crystal growth process. However, the impulses require sudden and intermittent changes to the rotation speed, which are difficult to implement through the soft rope connection. In this work, a small amplitude resonant perturbation to the rotation speed is being proposed to suppress chaos in the FSRL system. The system state, given by the swing angle between the rotation center on the vertical axis and the soft shaft, is observed by measuring the force on the soft shaft and by using the untraced Kalman filter. The control parameters are selected by calculating the Lyapunov exponent. As compared with the previous impulse control methods, the proposed small amplitude resonant perturbation method engenders a small continuous change instead of the sudden change in the rotation speed. In addition, the proposed method does not alter the average rotation speed, which complies with the crystal growth technique requirement. The effectiveness of the proposed chaos control method is validated by numerical simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Data Availability Statement

All data generated or analyzed during this study are included within the article.

References

  1. Ren, H.P., Zhou, Z.X., Grebogi, C.: Nonlinear dynamics in the flexible shaft rotating lifting system of silicon crystal puller using Czochralski method. Nonlinear Dyn. 102, 771–784 (2020)

    Article  Google Scholar 

  2. Ott, E., Grebogi, C., Yorke, J.A.: Controlling chaos. Phys. Rev. Lett. 64(11), 1196–1199 (1990)

    Article  MathSciNet  Google Scholar 

  3. Yang, T., Yang, L.B., Yang, C.M.: Impulsive control of Lorenz system. Phys. D. 110(1–2), 18–24 (1997)

    Article  MathSciNet  Google Scholar 

  4. Lima, R., Pettini, M.: Suppression of chaos by resonant parametric perturbations. Phys. Rev. A 41(2), 726–733 (1990)

    Article  MathSciNet  Google Scholar 

  5. Zhou, Z.X., Grebogi, C., Ren, H.P.: Parameter impulse control of chaos in crystal growth process. J. Cryst. Growth. 563, 126079 (2021)

    Article  Google Scholar 

  6. Zhou, Z.X., Ren, H.P., Grebogi, C.: Bi-directional impulse chaos control in crystal growth. Chaos 31, 53106 (2021)

    Article  MathSciNet  Google Scholar 

  7. Fronzoni, L., Giocondo, M., Pettini, M.: Experimental evidence of suppression of chaos by resonant parametric perturbations. Phys. Rev. A 43(12), 6483–6487 (1991)

    Article  Google Scholar 

  8. Lima, R., Pettini, M.: Parametric resonant control of chaos. Int. J. Bifurc. Chaos. 8(8), 1675–1684 (1998)

    Article  Google Scholar 

  9. Inaba, N., Sekikawa, M., Endo, T., Takashi, T.: Revealing the trick of taming chaos by weak harmonic perturbations. Int. J. Bifurc. Chaos. 13(10), 2905–2915 (2003)

    Article  MathSciNet  Google Scholar 

  10. Zhou, Y.F., Tse, C.K., Qiu, S.S., Chen, J.N.: An improved resonant parametric perturbation for chaos control with applications to control of DC/DC converters. Chin. Phys. B 14(1), 61–66 (2005)

    Article  Google Scholar 

  11. Yang, J.P., Jing, Z.J.: Inhibition of chaos in a pendulum equation. Chaos. Soliton. Fract. 35(4), 726–737 (2008)

  12. Yang, J.P., Jing, Z.J.: Control of chaos in a three-well duffing system. Chaos. Soliton. Fract. 41(3), 1311–1328 (2009)

    Article  MathSciNet  Google Scholar 

  13. Tamura, T., Inaba, N., Miyamichi, J.: Mechanism for taming chaos by weak harmonic perturbations. Phys. Rev. Lett. 89(19), 3824–3827 (1999)

    Article  Google Scholar 

  14. Chacón, R., García-Hoz, A.M., Miralles, J.J., Martínez, P.J.: Amplitude modulation control of escape from a potential well. Phys. Lett. A. 378, 1104–1112 (2014)

    Article  Google Scholar 

  15. Qu, Z.L., Hu, G., Yang, G.J., Qin, G.R.: Phase effect in taming non-autonomous chaos by weak harmonic perturbations. Phys. Rev. Lett. 74(10), 1736–1739 (1995)

    Article  Google Scholar 

  16. Chacón, R.: Role of ultrasubharmonic resonances in taming chaos by weak harmonic perturbations. Eurphys. Lett. 54(2), 148–153 (2001)

    Article  Google Scholar 

  17. Wu, G., Li, L.S., Cong, X.R.: Chaos control for coupling of the double-well duffing system based on random phase disturbance. Int. J. Theor. Phys. 52, 1956–1963 (2013)

    Article  MathSciNet  Google Scholar 

  18. Zambrano, S., Allaria, E., Brugioni, S., Leyva, I., Meucci, R., Sanjuán, M.A., Arecchi, F.T.: Phase control of intermittency in dynamical systems. Phys. Rev. E 74(1), 016202 (2006)

    Article  Google Scholar 

  19. Zambrano, S., Allaria, E., Brugioni, S., et al.: Numerical and experimental exploration of phase control of chaos. Chaos 16, 013111 (2006)

    Article  Google Scholar 

  20. Amer, Y.A., Bauomy, H.S., Sayed, M.: Vibration suppression in a twin-tail system to parametric and external excitations. Comput. Math. Appl. 58(10), 1947–1964 (2009)

    Article  Google Scholar 

  21. Li, L.S., Yu, H.D.: Chaos control of a class of parametrically excited Duffing’s system using a random phase. Chaos. Soliton. Fract. 44(7), 498–500 (2011)

    Article  Google Scholar 

  22. Chen, X.W., Jing, Z.J., Fu, X.G.: Chaos control in a pendulum system with excitations and phase shift. Nonlinear Dyn. 78(1), 317–327 (2014)

    Article  MathSciNet  Google Scholar 

  23. Chacón, R., Martínez, J.A.: Controlling escape from a potential well by reshaping periodic secondary excitations. Phys. Rev. E 83(1), 016201 (2011)

    Article  MathSciNet  Google Scholar 

  24. Chacón, R., Martínez, J.A., Miralles, J.J.: Impulse-induced optimum control of escape from a metastable state by periodic secondary excitations. Phys. Rev. E 85(6 Pt 2), 066207 (2012)

    Article  Google Scholar 

  25. Ren, H.P., Bai, C., Tian, K., Grebogi, C.: Dynamics of delay induced composite multi-scroll attractor and its application in encryption. Int. J. Nonlin. Mech. 94, 334–342 (2017)

    Article  Google Scholar 

Download references

Funding

This work was supported in part by the Shaanxi Provincial Special Support Program for Science and Technology Innovation Leader.

Author information

Authors and Affiliations

  1. Shaanxi Key Laboratory of Complex System Control and Intelligent Information Processing, Xi’an University of Technology, Xi’an, Shaanxi, 710048, China

    Zi-Xuan Zhou, Hai-Peng Ren & Celso Grebogi

  2. School of Computer Science and Engineering, North Minzu University, Yinchuan, Ningxia, 750021, China

    Zi-Xuan Zhou

  3. Institute for Complex System and Mathematical Biology, University of Aberdeen, Aberdeen, AB24 3UE, UK

    Celso Grebogi

Authors
  1. Zi-Xuan Zhou
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hai-Peng Ren
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Celso Grebogi
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hai-Peng Ren.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

Some function definitions are given in the following. For the elliptic integrals function of the first kind,

$$\begin{aligned} \rho =\int _{0}^{\varphi }\frac{dx}{\sqrt{1-m^2\sin ^2x}}, \end{aligned}$$
(A1)

its inverse function is written by:

$$\begin{aligned} \varphi =am(\rho ). \end{aligned}$$
(A2)

Then, Jacobian elliptic functions \(sn(\cdot )\) and \(dn(\cdot )\) are defined by:

$$\begin{aligned} sn(\cdot )=sn(\rho ,m)=\sin \varphi =\sin (am(\rho )), \end{aligned}$$
(A3)
$$\begin{aligned} dn(\cdot )=dn(\rho ,m)=\sqrt{1-m^2sn^2(\rho ,m)}. \end{aligned}$$
(A4)

The complete elliptic integral of the first kind is given by,

$$\begin{aligned} K=K(m)=\int _{0}^{\pi /2}\frac{dx}{\sqrt{1-m^2\sin ^2x}}. \end{aligned}$$
(A5)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, ZX., Ren, HP. & Grebogi, C. Suppressing chaos in crystal growth process using adaptive phase resonant perturbation. Nonlinear Dyn 108, 2655–2669 (2022). https://doi.org/10.1007/s11071-022-07333-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-022-07333-6

Keywords