Bifurcation dodge: avoidance of a thermoacoustic instability under transient operation

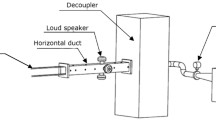
Abstract

Varying one of the governing parameters of a dynamical system may lead to a critical transition, where the new stable state is undesirable. In some cases, there is only a limited range of the bifurcation parameter that corresponds to that unwanted attractor, while the system runs problem-less otherwise. In this study, we present experimental results regarding a thermoacoustic system subject to two consecutive and mirrored supercritical Hopf bifurcations: the system exhibits high-amplitude thermoacoustic limit cycles for intermediate values of the bifurcation parameter. Changing quickly enough the bifurcation parameter, it was possible to dodge the unwanted limit cycles. A low-order model of the complex thermoacoustic system was developed, in order to describe this interesting transient dynamics. It was afterward used to assess the risk of exceeding an oscillation amplitude threshold as a function of the rate of change of the bifurcation parameter.

Appendices

Appendix A

Fig. 11

Simulation of the ramp dynamics with all the model’s parameters varying. Top: approximation of the identified $\nu (\dot{m}_{\text {air}})$, $\kappa (\dot{m}_{\text {air}})$ and $\varGamma (\dot{m}_{\text {air}})$ (blue lines), with simple functions (respectively, a half cosine, a sigmoid and a cosine—red lines). Center and bottom: Time evolution of the amplitude PDF $P(A;\,t)$ in the experiments and the one obtained solving the FPE with all the parameters varying with $\dot{m}_{\text {air}}$. (Color figure online)

Figure 11 shows the evolution of the PDF $P(A;\,t)$, when all the three parameters $\nu$, $\kappa$ and $\varGamma$ vary with the ramping of the bifurcation parameter, as shown in the top panels. In particular, the variation of the linear growth rate $\nu$ is approximated, as already done in the main body of the paper, with a half cosine fitted with the growth rates identified from the stationary experiments. The saturation constant dependence on the bifurcation parameter is approximated with the sigmoid function $\kappa (\dot{m}_{\text {air}})=k_1/(1+\exp {(-k_2\dot{m}_{\text {air}} +k_3)})+k_4$. The noise intensity variation is approximated with a cosine. One can observe in the bottom panel how the $P(A;\,t)$ obtained with this more complicated version of the model does not differ qualitatively from the one obtained with the simplified model and shown in Fig. 8, and reproduces qualitatively the experimental one, represented in the central panel for reference. It is important to remark that in this more complex model, the variation of each parameter is a direct function of the bifurcation parameter $\dot{m}_{\text {air}}$ only, and no inter-dependence between the three parameters $\nu$, $\kappa$ and $\varGamma$ is taken into account. That mutual dependence among parameters might be present in some physical system, including the one discussed in the present study. A further investigation of this aspect can be a topic for future work.

Appendix B

Given the stationary PDF $P_\infty (A)$:

$$\begin{aligned} P_\infty (A)=\mathcal {N}A\exp \left[ \frac{4\omega _0^2}{\varGamma }\left( \nu \frac{A^2}{2}-\kappa \frac{A^4}{32}\right) \right] \end{aligned}$$

(5)

with:

$$\begin{aligned} \begin{aligned} \mathcal {N}=\left\{ \sqrt{\frac{2\pi }{\kappa }\frac{\varGamma }{4\omega _0^2}}\exp \left( 2\frac{\nu ^2}{\kappa }\frac{4\omega _0^2}{\varGamma }\right) \ldots \right. \\ \left. \ldots \left[ 1+ \text {erf}\left( \nu \sqrt{\frac{2}{\kappa }\frac{4\omega _0^2}{\varGamma }}\right) \right] \right\} ^{-1} \end{aligned} \end{aligned}$$

(6)

The mean of the distribution is given by:

$$\begin{aligned} \begin{aligned} \langle A \rangle ={}&\mathcal {N}\pi \sqrt{\frac{2}{|\nu |\kappa ^3}}\exp \left( \frac{\nu ^2}{\kappa }\frac{4\omega _0^2}{\varGamma }\right) \ldots \\&\ldots \bigg \{2\frac{\nu ^3}{|\nu |}\left[ I_{-\frac{1}{4}}\left( \frac{\nu ^2}{\kappa }\frac{4\omega _0^2}{\varGamma }\right) + I_{\frac{3}{4}}\left( \frac{\nu ^2}{\kappa }\frac{4\omega _0^2}{\varGamma }\right) \right] \ldots \\&\ldots +\left( \frac{\varGamma }{4\omega _0^2}\kappa +2\nu ^2\right) I_{\frac{1}{4}}\left( \frac{\nu ^2}{\kappa }\frac{4\omega _0^2}{\varGamma }\right) \ldots \\&\ldots +2\nu ^2I_{\frac{5}{4}}\left( \frac{\nu ^2}{\kappa }\frac{4\omega _0^2}{\varGamma }\right) \bigg \}, \end{aligned} \end{aligned}$$

(7)

where $I_z(x)$ is the modified Bessel function of first kind. This formula is indefinite if $\nu =0$, where it tends to:

$$\begin{aligned} \langle A \rangle = \frac{2^{\frac{5}{4}}}{\sqrt{\pi }}\left( \frac{\varGamma }{4\omega _0^2\kappa }\right) ^\frac{1}{4}\gamma \left( \frac{3}{4}\right) , \end{aligned}$$

(8)

being $\gamma (x)$ the Euler gamma function.