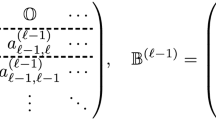Spectral collocation methods for the periodic solution of flexible multibody dynamics

Abstract

Many flexible multibody systems of practical interest exhibit a periodic response. This paper focuses on the implementation of the collocation version of the Fourier spectral method to determine periodic solutions of flexible multibody systems modeled via the finite element method. To facilitate the analysis and obtain governing equations presenting low-order nonlinearities, the motion formalism is adopted. Application of Fourier spectral methods requires global interpolation schemes that approximate the unknown fields over the entire period of response with exponential convergence characteristics. The classical spectral interpolation schemes were developed for linear fields and hence do not apply to the nonlinear configuration manifolds, such as $\mathrm {SO}(3)$ or $\mathrm {SE}(3)$, that are used to describe the kinematics of multibody systems. Furthermore, the configuration and velocity fields are related through nonlinear kinematic compatibility equations. Clearly, special procedures must be developed to adapt the Fourier spectral approach to flexible multibody systems. The spectral interpolation of motion is investigated; interpolation schemes based on the polar decomposition are proposed. Assembly of the linearized governing equations at all the grid points leads to the governing equations of the spectral method. Numerical examples illustrate the performance of the proposed approach.

Appendices

Appendix A: Dual numbers, vectors, matrices, and functions

Dual numbers were first introduced in the nineteenth century by Clifford [28]. Typically, they are written as , where a and $a^{o}$ are referred to as the primal and dual parts, respectively, and parameter $\epsilon$ is such that $\epsilon ^{n} = 0$ for $n \ge 2$. The product of two dual scalars now becomes . The zero and identity dual numbers are and , respectively. The inverse of a dual scalar is .

A dual vector is composed of two vectors of the same size . The inner product of two dual vectors is . The cross product of two dual vectors of size $3\times 1$ is , where notation $\tilde{(\cdot )}$ is the skew-symmetric dual matrix associated with . Dual vector is unit if , which is equivalent to $\underline{a}^{ T} \underline{a}= 1$ and $\underline{a}^\mathrm{{T}} \underline{a}^{o} = 0$.

Similarly, a dual matrix is composed of two matrices of the same size . The transpose of a dual matrix is . The identity dual matrix is defined as . The product of a dual matrix by a dual vector is found easily as . Dual matrix is orthogonal if , which is equivalent to $\underline{\underline{A}}^\mathrm{{T}} \underline{\underline{A}}= \underline{\underline{I}}$ and .

Consider a dual function of a dual variable, . Function is assumed to be analytic [33, 59], i.e., it is of the following form: , where J(a) is the primal part of dual function and notation $(\cdot )'$ indicates a derivative with respect to a. The derivative of dual function with respect to dual variable is a dual number, . Two important observations can be made: (1) the primal part of an analytic function depends on the primal part of its dual variable only and (2) the dual part of an analytic function is a linear function of the dual part of its dual variable. Because the magnitude of a dual number is not defined, dual numbers cannot be compared. The primal part of a dual function, J(a), can reach a minimum or maximum, whereas its dual part, $a^{o} J' (a)$, never reaches a minimum or maximum in a open set because it is a linear function of $a^{o}$. Minimization of a dual function is not meaningful.

Appendix B: Identities of matrix and vectors

This section presents a set of useful identities that are used throughout the paper. The identities involve a dual matrix, , of size $3\times 3$, and a dual vector, , of size $3\times 1$.

(38a)

(38b)

(38c)

(38d)

(38e)

(38f)

These identities can be verified easily.

Appendix C: The polar decomposition theorem

The polar decomposition theorem can be stated as follows.

Theorem 1

(Polar decomposition theorem) An invertible matrix, $\underline{\underline{G}}\in \mathbb {R}^{3\times 3}$, can be decomposed into the product of a rotation tensor, $\underline{\underline{R}}\in \mathrm {SO}(3)$, by a symmetric matrix, $\underline{\underline{S}}$, as $\underline{\underline{G}}= \underline{\underline{R}}\, \underline{\underline{S}}$. Matrices $\underline{\underline{R}}$ and $\underline{\underline{S}}$ are defined uniquely if matrix $[ \mathrm {tr}(\underline{\underline{S}}) \underline{\underline{I}}- \underline{\underline{S}}]$ is required to be positive definite.

Proof

Let the spectral decomposition of positive-definite matrix $\underline{\underline{G}}^\mathrm{{T}} \underline{\underline{G}}$ be $\underline{\underline{U}}^\mathrm{{T}} \mathrm {diag}(\lambda _{1}, \lambda _{2}, \lambda _{3})\underline{\underline{U}}$, where positive eigenvalues, $\lambda _{i}$, $i = 1, 2, 3$, satisfy $\lambda _{1} \le \lambda _{2} \le \lambda _{3}$. In view of identity $\underline{\underline{S}}^\mathrm{{T}} \underline{\underline{S}}= (\underline{\underline{R}}^\mathrm{{T}} \underline{\underline{G}})^\mathrm{{T}} (\underline{\underline{R}}^\mathrm{{T}} \underline{\underline{G}}) = \underline{\underline{G}}^\mathrm{{T}} \underline{\underline{G}}$, symmetric matrix $\underline{\underline{S}}$ can be chosen as $\underline{\underline{U}}^\mathrm{{T}}\mathrm {diag}(\pm \sqrt{\lambda _{1}},\pm \sqrt{\lambda _{2}},\pm \sqrt{\lambda _{3}})\underline{\underline{U}}$. Of these eight choices, two only, $\underline{\underline{U}}^\mathrm{{T}} \mathrm {diag}(\pm \sqrt{\lambda _{1}}, \sqrt{\lambda _{2}}, \sqrt{\lambda _{3}}) \underline{\underline{U}}$, render matrix $[ \mathrm {tr}(\underline{\underline{S}})\underline{\underline{I}}- \underline{\underline{S}}]$ positive definite. The sign of the lowest eigenvalue is determined by sign of $\det (\underline{\underline{G}}) = \det (\underline{\underline{R}}) \det (\underline{\underline{S}}) = \det (\underline{\underline{S}})$: Choose the positive or negative sign if $\mathrm {det}(\underline{\underline{G}})$ is positive or negative, respectively. $\square$

Remark 1

Polar decomposition theorem (1) differs slightly from the traditional polar decomposition theorem used in continuum mechanics [39, 60]. The proof above shows that eight different symmetric matrices $\underline{\underline{S}}$ satisfy multiplicative decomposition $\underline{\underline{G}}= \underline{\underline{R}}\, \underline{\underline{S}}$. The solution is made unique by imposing an additional condition: In the traditional and present versions of the theorem, matrices $\underline{\underline{S}}$ and $[ \mathrm {tr}(\underline{\underline{S}}) \underline{\underline{I}}- \underline{\underline{S}}]$ are required to be positive definite, respectively. When $\mathrm {det}(\underline{\underline{G}}) > 0$, the two theorems are identical.

Given an invertible matrix $\underline{\underline{G}}\in \mathbb {R}^{3\times 3}$, the following question is asked: Which rotation tensor $\underline{\underline{R}}\in \mathrm {SO}(3)$ is as close as possible to $\underline{\underline{G}}$? The problem is stated as

$$\begin{aligned} \min _{\underline{\underline{R}}\in \mathrm {SO}(3)} J(\underline{\underline{R}}) = \Vert \underline{\underline{R}}- \underline{\underline{G}}\Vert _{F}^{2}, \end{aligned}$$

(39)

where the closeness of the two matrices is defined as the square of the Frobenius norm of their difference.

Theorem 2

(Closest rotation tensor) The rotation tensor that satisfies minimization problem (39) is that provided by polar decomposition Theorem (1).

Proof

Defining $\underline{\underline{S}}= \underline{\underline{R}}^\mathrm{{T}} \underline{\underline{G}}$, the objective function becomes $J = \mathrm {tr}[ (\underline{\underline{R}}- \underline{\underline{G}})^\mathrm{{T}} (\underline{\underline{R}}- \underline{\underline{G}}) ] = \mathrm {tr}[ \underline{\underline{I}}+ \underline{\underline{G}}^\mathrm{{T}} \underline{\underline{G}}- \underline{\underline{S}}- \underline{\underline{S}}^\mathrm{{T}} ] = \mathrm {tr}(\underline{\underline{I}}+ \underline{\underline{G}}^\mathrm{{T}} \underline{\underline{G}}) - 2 \mathrm {tr}(\underline{\underline{S}})$ and its variation is $\delta J = - 2 \mathrm {tr}(\delta \underline{\underline{S}}) = 2 \mathrm {tr}(\tilde{\delta \psi }\, \underline{\underline{S}})$, where $\tilde{\delta \psi }= \underline{\underline{R}}^\mathrm{{T}} \delta \underline{\underline{R}}$. Finally, trace identity (38e) yields $\delta J = - 4 \underline{\delta \psi }^\mathrm{{T}} \mathrm {axial}(\underline{\underline{S}}) = 0$, which implies that matrix $\underline{\underline{S}}$ must be symmetric. For the objective function to reach its minimum, its Hessian must be positive definite. Taking a second-order variation yields $\delta ^{2} J = - 2 \underline{\delta \psi }^\mathrm{{T}} \mathrm {axial}(\delta \underline{\underline{S}})$, leading to $\delta ^{2} J = 2 \underline{\delta \psi }^\mathrm{{T}} [\mathrm {tr}{(\underline{\underline{S}})} \underline{\underline{I}}- \underline{\underline{S}}] \underline{\delta \psi }$, where matrix $[\mathrm {tr}{(\underline{\underline{S}})} \underline{\underline{I}}- \underline{\underline{S}}]$ is the Hessian. Clearly, polar decomposition theorem (1) provides uniquely defined rotation tensor $\underline{\underline{R}}$ and matrix $\underline{\underline{S}}$ that satisfy the two required conditions: $\underline{\underline{S}}$ is symmetric and $[\mathrm {tr}{(\underline{\underline{S}})} \underline{\underline{I}}- \underline{\underline{S}}]$ is positive definite.

The polar decomposition theorem is now generalized to dual matrices.

Theorem 3

(Dual polar decomposition theorem) An invertible dual matrix, , can be decomposed into the product of a dual orthogonal matrix, , by a symmetric dual matrix, , as . Matrices and are defined uniquely if it is also required that matrix $[ \mathrm {tr}(\underline{\underline{S}}) \underline{\underline{I}}- \underline{\underline{S}}]$ be positive definite, where $\underline{\underline{S}}$ is the primal part of dual matrix .

Proof

To prove the theorem, dual matrices and will be constructed and the solution will be shown to be unique. First, dual identity is expanded as $(\underline{\underline{G}}+ \epsilon \underline{\underline{G}}^{o}) = (\underline{\underline{R}}+ \epsilon \underline{\underline{R}}^{o}) (\underline{\underline{S}}+ \epsilon \underline{\underline{S}}^{o})$, which implies

$$\begin{aligned}&\underline{\underline{G}}= \underline{\underline{R}}\, \underline{\underline{S}}, \end{aligned}$$

(40a)

$$\begin{aligned}&\underline{\underline{G}}^{o} = \underline{\underline{R}}\, \underline{\underline{S}}^{o} + \underline{\underline{R}}^{o} \underline{\underline{S}}. \end{aligned}$$

(40b)

Equation (40a) expresses Theorem (1), i.e., rotation tensor $\underline{\underline{R}}$ and symmetric matrix $\underline{\underline{S}}$ are defined uniquely. Equation (40b) implies $\underline{\underline{R}}^{ T} \underline{\underline{G}}^{o} = \underline{\underline{S}}^{o} + (\underline{\underline{R}}^{ T} \underline{\underline{R}}^{o}) \underline{\underline{S}}$, where matrix $\underline{\underline{R}}^{ T} \underline{\underline{R}}^{o} = \tilde{z}$ is antisymmetric because motion tensor is orthogonal. Because matrix $\underline{\underline{S}}^{o}$ must be symmetric, $\mathrm {axial}(\underline{\underline{S}}^{o}) = \underline{0}$, and extracting the axial part of this equation yields $\mathrm {axial}(\underline{\underline{R}}^{ T} \underline{\underline{G}}^{o}) = \mathrm {axial}[\tilde{z}\underline{\underline{S}}]$. Identity (38a) now yields $[\mathrm {tr}{(\underline{\underline{S}})} \underline{\underline{I}}- \underline{\underline{S}}] \underline{z}= 2 \mathrm {axial}(\underline{\underline{R}}^{ T} \underline{\underline{G}}^{o} )$, a linear system that can be solved to find $\underline{z}$. The dual parts of motion tensor and symmetric matrix are found as $\underline{\underline{R}}^{o} = \underline{\underline{R}}\tilde{z}$ and $\underline{\underline{S}}^{o} = \underline{\underline{R}}^{ T} \underline{\underline{G}}^{o} - \tilde{z}\underline{\underline{S}}$, respectively. $\square$

Given an invertible dual matrix , the following question is asked: Which motion tensor is as close as possible to ? By analogy with Eq. (39), the following minimization problem is introduced

(41)

As discussed earlier, the minimization of a function of dual numbers is devoid of meaning. Therefore, notation “” is now defined as follows.

Definition 1

(Minimization of a dual function) The minimization of a dual function of dual variables, , implies the satisfaction of two conditions: (1) the variation of the objective function must vanish, , and (2) the primal part of the objective function must achieve a minimum.

As discussed in “Appendix A,” the primal part of a dual function can reach a minimum, whereas its dual part never reaches a minimum in a open set because it is a linear function of the dual part of its variable. Definition (1) does not require the minimization of the dual part of the function, bypassing the problem. Note that the vanishing of the variation of the primal part of the objective function is a prerequisite for its minimization. An alternative statement of definition (1) reads: The minimization of a function of dual variables implies the minimization of its primal part and the stationarity of its dual part.

Theorem 4

(Closest motion tensor) The motion tensor that satisfies dual minimization problem (41) is that provided by dual polar decomposition Theorem (3).

Proof

Defining , the objective function becomes and its variation is , where . Finally, trace identity (38e) yields , which implies that dual matrix must be symmetric. The objective function is evaluated as . The minimization of its primal part is expressed by minimization problem (39), which is solved by the polar decomposition theorem; see Theorem (2). Clearly, dual polar decomposition theorem (3) provides uniquely defined motion tensor and matrix that satisfy the two required conditions: is symmetric and $[\mathrm {tr}{(\underline{\underline{S}})} \underline{\underline{I}}- \underline{\underline{S}}]$ is positive definite.

$\square$