Skip to main content
SpringerLink
Log in

Applications of integral bifurcation method together with homogeneous balanced principle on investigating exact solutions of time fractional nonlinear PDEs

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

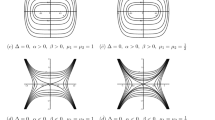
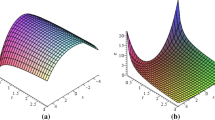
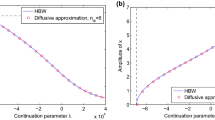
Abstract

In this paper, it is verified that the fractional chain rule appeared in some references does not hold under Riemann–Liouville definition and Caputo definition of fractional derivative. It implies that this chain rule is invalid on searching exact solutions of fractional nonlinear partial differential equations (PDEs). Avoiding this chain rule, a new way of investigating exact solutions of fractional nonlinear PDEs is introduced. As examples, a series of time fractional nonlinear PDEs with diffusion and convection terms are studied. Different kinds of exact solutions of these equations are obtained, their dynamical properties are discussed, and the profiles of several representative exact solutions are illustrated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Tan, W., Pan, W., Xu, M.: A note on unsteady flows of a viscoelastic fluid with the fractional Maxwell model between two parallel plates. Int. J. Non-Linear Mech. 38(5), 645–650 (2003)

    Article  MATH  Google Scholar 

  2. Hayat, T., Nadeem, S., Asghar, S.: Periodic unidirectional flows of a viscoelastic fluid with the fractional Maxwell model. Appl. Math. Comput. 151(1), 153–161 (2004)

    MathSciNet  MATH  Google Scholar 

  3. Tripathi, D., Pandey, S.K., Das, S.: Peristaltic flow of viscoelastic fluid with fractional Maxwell model through a channel. Appl. Math. Comput. 215(10), 3645–3654 (2010)

    MathSciNet  MATH  Google Scholar 

  4. Grigorenko, I., Grigorenko, E.: Chaotic dynamics of the fractional Lorenz system. Phys. Rev. Lett. 91(3), 034101 (2003)

    Article  Google Scholar 

  5. Pei, S.C., Ding, J.J.: Relations between Gabor transforms and fractional Fourier transforms and their applications for signal processing. IEEE Trans. Signal Process. 55(10), 4839–4850 (2007)

    Article  MathSciNet  Google Scholar 

  6. Sejdić, E., Djurović, I., Stanković, L.: Fractional Fourier transform as a signal processing tool: an overview of recent developments. Signal Process. 91(6), 1351–1369 (2011)

    Article  MATH  Google Scholar 

  7. Lohmann, A.W., Mendlovic, D., Zalevsky, Z., Dorsch, R.G.: Some important fractional transformations for signal processing. Opt. Commun. 125(1), 18–20 (1996)

    Article  Google Scholar 

  8. Baleanu, D., Machado, J.A.T., Luo, A.C. (eds.): Fractional Dynamics and Control. Springer, Berlin (2011)

    MATH  Google Scholar 

  9. Dorcak, L.: Numerical models for the simulation of the fractional-order control systems (2002). arXiv preprint arXiv:math/0204108

  10. Sakthivel, R., Mahmudov, N.I., Nieto, J.J.: Controllability for a class of fractional-order neutral evolution control systems. Appl. Math. Comput. 218(20), 1033–10340 (2012)

    MathSciNet  MATH  Google Scholar 

  11. Metzler, R., Barkai, E., Klafter, J.: Anomalous diffusion and relaxation close to thermal equilibrium: a fractional Fokker–Planck equation approach. Phys. Rev. Lett. 82(18), 3563 (1999)

    Article  Google Scholar 

  12. Metzler, R., Glöckle, W.G., Nonnenmacher, T.F.: Fractional model equation for anomalous diffusion. Physica A: Stat. Mech. Appl. 211(1), 13–24 (1994)

    Article  Google Scholar 

  13. Henry, B.I., Langlands, T.A.M., Wearne, S.L.: Anomalous diffusion with linear reaction dynamics: from continuous time random walks to fractional reaction–diffusion equations. Phys. Rev. E 74(3), 031116 (2006)

    Article  MathSciNet  Google Scholar 

  14. Anh, V.V., Leonenko, N.N.: Scaling laws for fractional diffusion-wave equations with singular initial data. Statist. Probab. Lett. 48, 239–252 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  15. Ahmed, E., Elgazzar, A.S.: On fractional order differential equations model for nonlocal epidemics. Physica A: Stat. Mech. Appl. 379(2), 607–614 (2007)

    Article  Google Scholar 

  16. El-Sayed, A.M.A., Rida, S.Z., Arafa, A.A.M.: Exact solutions of fractional-order biological population model. Commun. Theor. Phys. 52(6), 992 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  17. Liu, F., Burrage, K.: Novel techniques in parameter estimation for fractional dynamical models arising from biological systems. Comput. Math. Appl. 62(3), 822–833 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  18. Jamil, M., Khan, A.N., Shahid, N.: Fractional magnetohydrodynamics Oldroyd-B fluid over an oscillating plate. Therm. Sci. 17(4), 997–1011 (2013)

    Article  Google Scholar 

  19. Moustafa, E.S.: MHD of a fractional viscoelastic fluid in a circular tube. Mech. Res. Commun. 33(2), 261–268 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  20. Zafar, A.A., Vieru, D., Akhtar, S.: Magnetohydrodynamics of rotating fractional second grade fluid in porous medium. J. Prime Res. Math. 10, 45–58 (2015)

    MathSciNet  Google Scholar 

  21. Sahadevan, R., Bakkyaraj, T.: Invariant subspace method and exact solutions of certain nonlinear time fractional partial differential equations. Fract. Calc. Appl. Anal. 18(1), 146–162 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  22. Daftardar-Gejji, V., Jafari, H.: Adomian decomposition: a tool for solving a system of fractional differential equations. J. Math. Anal. Appl. 301(2), 508–518 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  23. Bakkyaraj, T., Sahadevan, R.: An approximate solution to some classes of fractional nonlinear partial differentialdifference equation using Adomian decomposition method. J. Fract. Calc. Appl. 5(1), 37–52 (2014)

    MathSciNet  Google Scholar 

  24. Eslami, M., Vajargah, B.F., Mirzazadeh, M., Biswas, A.: Applications of first integral method to fractional partial differential equations. Indian J. Phys. 88(2), 177–184 (2014)

    Article  Google Scholar 

  25. Bakkyaraj, T., Sahadevan, R.: Approximate analytical solution of two coupled time fractional nonlinear Schrodinger equations. Int. J. Appl. Comput. Math. 2(1), 113–135 (2016)

    Article  MathSciNet  Google Scholar 

  26. Bakkyaraj, T., Sahadevan, R.: On solutions of two coupled fractional time derivative Hirota equations. Nonlinear Dyn. 77(4), 1309–1322 (2014)

    Article  MathSciNet  Google Scholar 

  27. Sahadevan, R., Bakkyaraj, T.: Invariant analysis of time fractional generalized Burgers and Korteweg–de Vries equations. J. Math. Anal. Appl. 393(2), 341–347 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  28. Bakkyaraj, T., Sahadevan, R.: Invariant analysis of nonlinear fractional ordinary differential equations with Riemann–Liouville derivative. Nonlinear Dyn. 80(1), 447–455 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  29. Harris, P.A., Garra, R.: Analytic solution of nonlinear fractional Burgers-type equation by invariant subspace method. Nonlinear Stud. 20(4), 471–481 (2013)

    MathSciNet  MATH  Google Scholar 

  30. Sahadevan, R., Prakash, P.: Exact solution of certain time fractional nonlinear partial differential equations. Nonlinear Dyn. 85(1), 659–673 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  31. Odibat, Z.M., Shaher, M.: The variational iteration method: An efficient scheme for handling fractional partial differential equations in fluid mechanics. Comput. Math. Appl. 58, 2199–2208 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  32. Wu, G., Lee, E.W.M.: Fractional variational iteration method and its application. Phys. Lett. A 374(25), 2506–2509 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  33. Momani, S., Zaid, O.: Comparison between the homotopy perturbation method and the variational iteration method for linear fractional partial differential equations. Comput. Math. Appl. 54(7), 910–919 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  34. Jumarie, G.: Fractional partial differential equations and modified Riemann–Liouville derivative new methods for solution. J. Appl. Math. Comput. 24(1–2), 31–48 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  35. Jumarie, G.: Modified Riemann–Liouville derivative and fractional Talor series of non-differentiable functions further results. Comput. Math. Appl. 51(9–10), 1367–1376 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  36. Jumarie, G.: Cauchy’s integral formula via the modified Riemann–Liouville derivative for analytic functions of fractional order. Appl. Math. Lett. 23(12), 1444–1450 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  37. Elsayed, M.E.Z., Yasser, A.A., Reham, M.A.S.: The fractional complex transformation for nonlinear fractional partial differential equations in the mathematical physics. J. Assoc. Arab Univ. Basic Appl. Sci. 19, 59–69 (2016)

    Google Scholar 

  38. Li, Z.-B., Zhu, W.-H., He, J.-H.: Exact solutions of time-fractional heat conduction equation by the fractional complex transform. Thermal Sci. 16(2), 335–338 (2012)

    Article  Google Scholar 

  39. Li, Z.-B., He, J.-H.: Fractional complex transform for fractional differential equations. Math. Comput. Appl. 15(5), 970–973 (2010)

    MathSciNet  MATH  Google Scholar 

  40. Ahmet, B., Özkan, G., Esin, A., Yusuf, P.: Functional variable method for the nonlinear fractional differential equations. In: Proceeding of the International Conference on Numerical Analysis and Applied Mathematics 2014 (ICNAAM-2014). https://doi.org/10.1063/1.4912955

  41. He, J.-H.: Geometrical explanation of the fractional complex trnsform and derivative chain rule for fractional calculus. Phys. Lett. A 376, 257–259 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  42. Tarasov, V.E.: On chain rule for fractional derivatives. Commun. Nonlinear Sci. Numer. Simul. 30(1), 1–4 (2016)

    Article  MathSciNet  Google Scholar 

  43. Rui, W.: Applications of homogenous balanced principle on investigating exact solutions to a series of time fractional nonlinear PDEs. Commun. Nonlinear Sci. Numer. Simul. 47, 253–266 (2017)

    Article  MathSciNet  Google Scholar 

  44. Rui, W., He, B., Long, Y., et al.: The integral bifurcation method and its application for solving a family of third-order dispersive PDEs. Nonlinear Anal.: Theory Methods Appl. 69(4), 1256–1267 (2008)

  45. Rui, W., He, B., Xie, S., et al.: Application of the integral bifurcation method for solving modified Camassa–Holm and Degasperis–Procesi equations. Nonlinear Anal.: Theory Methods Appl. 71(7), 3459–3470 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  46. Rui, W.: The integral bifurcation method combined with factoring technique for investigating exact solutions and their dynamical properties of a generalized Gardner equation. Nonlinear Dyn. 76(2), 1529–1542 (2014)

  47. Bluman, G., Kumei, S.: On the remarkable nonlinear diffusion equation \((\partial /\partial x)[a(u+b)-2(\partial u/\partial x)]-(\partial u/\partial t)=0.\). J. Math. Phys. 21(5), 1019–1023 (1980)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The project is supported by the Natural Science Foundation of China (No. 11361023), the Natural Science Foundation of Scientific and Technical Committee of Chongqing City (No. cstc2014jcyjA00014) and the Natural Science Foundation of Chongqing Normal University (No. 13XLR20).

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Chongqing Normal University, Chongqing, 401331, People’s Republic of China

    Weiguo Rui

Authors
  1. Weiguo Rui
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Weiguo Rui.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rui, W. Applications of integral bifurcation method together with homogeneous balanced principle on investigating exact solutions of time fractional nonlinear PDEs. Nonlinear Dyn 91, 697–712 (2018). https://doi.org/10.1007/s11071-017-3904-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-017-3904-4

Keywords

Search

Navigation