Skip to main content
SpringerLink
Log in

\(\varvec{(2+1)}\)-Dimensional nonlinear Rossby solitary waves under the effects of generalized beta and slowly varying topography

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

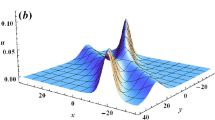
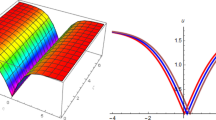
In this paper, \((2+1)\)-dimensional nonlinear Rossby waves are considered with the generalized beta, the dissipation and the topography which includes both basic part and slowly varying part with time. Starting with a barotropic quasi-geostrophic potential vorticity equation, by using methods of multiscales and perturbation expansions, a generalized forced Zakharov–Kuznetsov equation is obtained in describing the evolution of Rossby wave amplitude. The effects of generalized beta, topography along with latitude and slowly variation with time are all included, indicating that the generalized beta is an essential factor in inducing the nonlinear Rossby solitary waves and the other two are both important factors for the evolution of Rossby wave amplitude. Periodic and solitary wave solutions of Zakharov–Kuznetsov equation are obtained by the elliptic function expansion method; meanwhile, solitary wave solution of generalized forced Zakharov–Kuznetsov equation is obtained by reduced differential transform method. At last, graphical presentations for solitary wave amplitude with different dissipations and slowly varying topographies with time are shown by the Mathematica.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Long, R.R.: Solitary waves in the westerlies. J. Atmos. Sci. 21(3), 197–200 (1964)

    Article  Google Scholar 

  2. Redekopp, L.G.: On the theory of solitary Rossby waves. J. Fluid Mech. 82, 725–745 (1977)

    Article  MATH  MathSciNet  Google Scholar 

  3. Wadati, M.: The modified Korteweg–deVries equation. J. Phys. Soc. Jpn. 34, 1289–1296 (1973)

    Article  MATH  Google Scholar 

  4. Redekopp, L.G., Weidman, P.D.: Solitary Rossby waves in zonal shear flows and their interactions. J. Atmos. Sci. 35, 790–804 (1978)

    Article  Google Scholar 

  5. Boyd, J.P.: Equatorial solitary waves. Part I: Rossby solitons. J. Phys. Ocean. 10, 1699–1718 (1980)

    Article  Google Scholar 

  6. Boyd, J.P.: Equatorial solitary waves. Part 2: Rossby solitons. J. Phys. Ocean. 13, 428–449 (1983)

    Article  Google Scholar 

  7. Li, M.C., Xue, J.S.: Solitary Rossby waves of tropical atmospheric motion. Acta Meteorol. Sin. 42, 259–268 (1984). (in Chinese)

    Google Scholar 

  8. Ono, H.: Algebraic Rossby wave soliton. J. Phys. Soc. Jpn. 50(8), 2757–2761 (1981)

    Article  MathSciNet  Google Scholar 

  9. Luo, D.H., Ji, L.R.: A theory of blocking formation in the atmosphere. Sci. China 33(3), 323–333 (1989)

    MathSciNet  Google Scholar 

  10. Yang, H., Zhao, Q., Yin, B., Dong, H.: A new integro-differential equation for Rossby solitary waves with topography effect in deep rotational fluids. Abstr. Appl. Anal. 2013, 597807 (2013)

    MathSciNet  Google Scholar 

  11. Yang, H.W., Yang, D.Z., Shi, Y.L., Jin, S.S., Yin, B.S.: Interaction of algebraic Rossby solitary waves with topography and atmospheric blocking. Dyn. Atmos. Oceans 05, 001 (2015)

    Google Scholar 

  12. Yang, H., Yin, B., Shi, Y., Wang, Q.: Forced ILW-Burgers equation as a model for Rossby solitary waves generated by topography in finite depth fluids. J. Appl. Math. 2012 (2012). Article ID 491343

  13. Shi, Y.L., Yin, B.S., Yang, H.W., Yang, D.Z, Xu, Z.H.: Dissipative nonlinear Schrödinger equation for envelope solitary Rossby waves with dissipation effect in stratified fluids and its solution. Abstr. Appl. Anal. 2014 (2014). Article ID 643652

  14. Le, K.C., Nguyen, L.T.K.: Amplitude modulation of waves governed by Korteweg–de Vries equation. Int. J. Eng. Sci. 83, 117 (2014)

    Article  MathSciNet  Google Scholar 

  15. Le, K.C., Nguyen, L.T.K.: Energy Methods in Dynamics. Springer, Heidelberg (2014)

    Book  MATH  Google Scholar 

  16. Le, K.C., Nguyen, L.T.K.: Amplitude modulation of water waves governed by Boussinesq’s equation. Nonlinear Dyn. 81, 659 (2015)

    Article  MATH  MathSciNet  Google Scholar 

  17. Liu, S.K., Tan, B.K.: Rossby waves with the change of \(\beta \). J. Appl. Math. Mech. 13(1), 35–44 (1992). (in Chinese)

    MathSciNet  Google Scholar 

  18. Luo, D.H.: Solitary Rossby waves with the beta parameter and dipole blocking. J. Appl. Meteorol. 6, 220–227 (1995). (in Chinese)

    Google Scholar 

  19. Song, J., Yang, L.G.: Modified KdV equation for solitary Rossby waves with \(\beta \) effect in barotropic fluids. Chin. Phys. B 18(07), 2873–2877 (2009)

    Article  Google Scholar 

  20. Song, J., Liu, Q.S., Yang, L.G.: Beta effect and slowly changing topography Rossby waves in a shear flow. Acta Phys. Sin. 61(21), 210510 (2012)

    Google Scholar 

  21. Gottwalld, G.A.: The Zakharov–Kuznetsov equation as a two-dimensional model for nonlinear Rossby wave (2009). arXiv: org/abs/nlin/031

  22. Yang, H.W., Xu, Z.H., Yang, D.Z., Feng, X.R., Yin, B.S., Dong, H.H.: ZK–Burgers equation for three-dimensional Rossby solitary waves and its solutions as well as chirp effect. Adv. Differ. Equ. 2016, 167 (2016). doi:10.1186/s13662-016-0901-8

    Article  MathSciNet  Google Scholar 

  23. Karl, R.H., Melville, W.K., Miles, J.W.: On interfacial solitary waves over slowly varying topography. J. Fluid Mech. 149, 305–317 (1984)

    Article  MATH  MathSciNet  Google Scholar 

  24. Song, J., Yang, L.G., Liu, Q.S.: Nonlinear Rossby waves excited slowly changing underlying surface and dissipation. Acta Phys. Sin. 63(6), 060401 (2014). doi:10.7498/aps.63.060401

  25. Da, C.J., Chou, J.F.: Kdv equation with a forcing term for the evolution of the amplitude of Rossby waves along a slowly changing topography. Acta Phys. Sin. 57, 2595 (2008)

    Google Scholar 

  26. Abdou, M.A.: New solitons and periodic wave solutions for nonlinear physical models. Nonlinear Dyn. 52, 129 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  27. Ma, W.X., Zhang, Y., Tang, Y.N., Tu, J.Y.: Hirota bilinear equations with linear subspaces of solutions. Appl. Math. Comput. 218, 7174 (2012)

    MATH  MathSciNet  Google Scholar 

  28. Liu, S.K., Fu, Z.T., Liu, S.D., Zhao, Q.: Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A 289, 69–74 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  29. Zedan, H.A., Aladrous, E., Shapll, S.: Exact solutions for a perturbed nonlinear Schröinger equation by using Baklund transformations. Nonlinear Dyn. 74, 1145 (2013)

    Article  MATH  Google Scholar 

  30. Liao, S.J.: The proposed homotopy analysis technique for the solution of nonlinear problems. Ph.D. Thesis, Shanghai Jiao Tong University (1992)

  31. Adomian, G.A.: Review of the decomposition method and some recent results for nonlinear equations. Comput. Math. Appl. 21, 101–127 (1991)

    Article  MATH  MathSciNet  Google Scholar 

  32. Wang, M.L.: Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics. Phys. Lett. A 216, 67 (1996)

    Article  MATH  Google Scholar 

  33. Fu, Z.T., Liu, S.K., Liu, S.D., Zhao, Q.: New Jacobi elliptic function expansion and new periodic solutions of nonlinear wave equations. Phys. Lett. A 290, 72–6 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  34. He, J.H.: Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 178(3), 257 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  35. He, J.H.: Some asymptotic methods for strongly nonlinear equations. Int. J. Mod. Phys. B 20(10), 1141 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  36. Omer, A., Yildiray, K.: Reduced differential transform method for \((2+1)\) dimensional type of the Zakharov–Kuznetsov ZK \((n,m)\) equations. Preprint (2014). arXiv:1406.5834

  37. Fu, Z.T., Liu, S.K., Liu, S.D.: Multiple structures of two-dimensional nonlinear Rossby wave. Chaos Solitons Fractals 24, 383–390 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  38. Ma, H.C., Yu, Y.D., Ge, D.J.: The auxiliary equation method for solving the Zakharov–Kuznetsov (ZK) equation. Comput. Math. Appl. 58, 2523–2527 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  39. Caillol, P., Grimshaw, R.H.: Rossby elevation waves in the presence of a critical layer. Stud. Appl. Math. 120, 35–64 (2008)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors thank for the very valuable comments from reviewers and constructive suggestions from managing editor and assistant editor which greatly improved the quality of the paper. This project was supported by the National Natural Science Foundation of China (Grant Nos. 11362012, 11562014) and the Sciences of Inner Mongolia University of Technology (Grant No. ZD201411).

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Inner Mongolia University, Hohhot, 010021, China

    Ruigang Zhang, Liangui Yang & Quansheng Liu

  2. College of Sciences, Inner Mongolia University of Technology, Hohhot, 010051, China

    Jian Song

Authors
  1. Ruigang Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Liangui Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jian Song
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Quansheng Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Liangui Yang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, R., Yang, L., Song, J. et al. \(\varvec{(2+1)}\)-Dimensional nonlinear Rossby solitary waves under the effects of generalized beta and slowly varying topography. Nonlinear Dyn 90, 815–822 (2017). https://doi.org/10.1007/s11071-017-3694-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-017-3694-8

Keywords

Search

Navigation