Skip to main content
SpringerLink
Log in

Nonlinear normal modes of a shallow arch with elastic constraints for two-to-one internal resonances

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

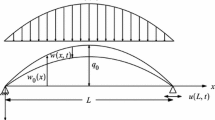
Abstract

The nonlinear normal modes (NNMs) of an elastically constrained (EC) shallow arch in the case of two-to-one internal resonance are constructed, and the effects of the vertical and rotational elastic boundary constraints are studied. The multiple scales method is directly applied to obtain the second-order uniform-expansion solution and the modulation equations from the dimensionless integral–partial–differential equation of motion. The elastic constraints have a corresponding relationship with the coefficients of modulation equations and influence the natural frequencies and modes, as demonstrated by solving the algebraic eigenvalue equation. The stability of the uncoupled single-mode and coupled-mode motions for the nonlinear system is investigated. Then the shape functions, activation conditions and space–time evolutions accounting for the two-to-one internally resonant NNMs for vertical and rotational elastic constraints are examined. The results show that the vertical and rotational elastic constraints play a fundamental role in the nonlinear dynamic phenomena of the EC shallow arch.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

References

  1. Blair, K.B., Krousgrill, C.M., Farris, T.N.: Non-linear dynamic response of shallow arches to harmonic forcing. J. Sound Vib. 194(3), 353–367 (1996)

    Article  MathSciNet  Google Scholar 

  2. Levitas, J., Singer, J., Weller, T.: Global dynamic stability of a shallow arch by Poincaré-like simple cell mapping. Int. J. Non-Linear Mech. 32(2), 411–424 (1997)

    Article  MATH  Google Scholar 

  3. Lakrad, F., Schiehlen, W.: Effects of a low frequency parametric excitation. Chaos Solitons Fractals 22(5), 1149–1164 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  4. Tien, W.M., Namachchivaya, N.S., Bajaj, A.K.: Nonlinear dynamics of a shallow arch under periodic excitation, I: 1:2 internal resonance. Int. J. Non-Linear Mech. 23(3), 349–366 (1994)

    Article  Google Scholar 

  5. Tien, W.M., Namachchivaya, N.S., Malhotra, N.: Non-linear dynamics of a shallow arch under periodic excitation, II: 1:1 internal resonance. Int. J. Non-Linear Mech. 29(3), 367–386 (1994)

    Article  MATH  Google Scholar 

  6. Malhotra, N., Namachchivaya, N.S.: Chaotic dynamic of shallow arch structures under 1:2 resonance. J. Eng. Mech. 123(6), 612–619 (1997)

    Article  Google Scholar 

  7. Malhotra, N., Namachchivaya, N.S.: Chaotic motion of shallow arch structures under 1:1 internal resonance. J. Eng. Mech. 123(6), 620–627 (1997)

    Article  Google Scholar 

  8. Bi, Q., Dai, H.H.: Analysis of non-linear dynamics and bifurcations of a shallow arch subjected to periodic excitation with internal resonance. J. Sound Vib. 233(4), 557–571 (2000)

    Article  Google Scholar 

  9. Thomsen, J.J.: Chaotic vibrations of non-shallow arches. J. Sound Vib. 153(2), 239–258 (1992)

    Article  MATH  Google Scholar 

  10. Benedettini, F., Alaggio, R., Zulli, D.: Nonlinear coupling and instability in the forced dynamics of a non-shallow arch: theory and experiments. Nonlinear Dyn. 68(4), 505–517 (2012)

    Article  Google Scholar 

  11. Kong, X.R., Wang, B.L., Hu, J.D.: Dynamic snap buckling of an elastoplastic shallow arch with elastically supported and Clamped ends. Comput. Struct. 55(1), 163–166 (1995)

    Article  MATH  Google Scholar 

  12. Xu, J.X., Huang, H., Zhang, P.Z., Zhou, J.Q.: Dynamic stability of shallow arch with elastic supports-application in the dynamic stability analysis of inner winding of transformer during short circuit. Int. J. Non-Linear Mech. 37(4–5), 909–920 (2002)

    Article  MATH  Google Scholar 

  13. Pi, Y.L., Bradford, M.A.: In-plane stability of preloaded shallow arches against dynamic snap-through accounting for rotational end restraints. Eng. Struct. 56, 1496–1510 (2013)

    Article  Google Scholar 

  14. Pi, Y.L., Bradford, M.A.: Non-linear buckling and postbuckling analysis of arches with unequal rotational end restraints under a central concentrated load. Int. J. Solids Struct. 49(26), 3762–3773 (2012)

    Article  Google Scholar 

  15. Lee, S.Y., Sheu, J.J., Lin, S.M.: In-plane vibrational analysis of rotating curved beam with elastically restrained root. J. Sound Vib. 315(4–5), 1086–1102 (2008)

    Article  Google Scholar 

  16. Bradford, M.A., Wang, T., Pi, Y.L., Gilbert, R.I.: In-plane stability of parabolic arches with horizontal spring supports, I: theory. J. Struct. Eng. 133(8), 1130–1137 (2007)

    Article  Google Scholar 

  17. Wang, T., Bradford, M.A., Gilbert, R.I., Pi, Y.L.: In-plane stability of parabolic arches with horizontal spring supports, II: experiments. J. Struct. Eng. 133(8), 1138–1145 (2007)

    Article  Google Scholar 

  18. Lacarbonara, W., Rega, G., Nayfeh, A.H.: Resonant non-linear normal modes, Part I: analytical treatment for structural one dimensional systems. Int. J. Non-Linear Mech. 38(6), 851–872 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  19. Lacarbonara, W., Rega, G.: Resonant non-linear normal modes, Part II: activation orthogonality conditions for shallow structural systems. Int. J. Non-Linear Mech. 38(6), 873–887 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  20. Lacarbonara, W., Arafat, H.N., Nayfeh, A.H.: Non-linear interactions in imperfect beams at veering. Int. J. Non-Linear Mech. 40(7), 987–1003 (2005)

    Article  MATH  Google Scholar 

  21. Rosenberg, R.M.: The normal modes of nonlinear N-degree-of freedom systems. ASME J. Appl. Mech. 29(1), 7–14 (1962)

    Article  MATH  Google Scholar 

  22. Shaw, S.W., Pierre, C.: Nonlinear normal modes and invariant manifold. J. Sound Vib. 150(1), 170–173 (1991)

    Article  MathSciNet  Google Scholar 

  23. Jiang, D., Pierre, C., Shaw, S.W.: The construction of nonlinear normal modes for systems with internal resonance. Int. J. Nonlinear Mech. 40(5), 729–746 (2005)

    Article  MATH  Google Scholar 

  24. Nayfeh, A.H., Nayfeh, S.A.: On nonlinear modes of continuous systems. ASME J. Vib. Acoust. 116(1), 129–136 (1994)

    Article  Google Scholar 

  25. King, M.E., Vakakis, A.F.: An energy-based approach to computing resonant nonlinear normal modes. ASME J. Appl. Mech. 63(3), 810–819 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  26. Pellicano, F., Vakakis, A.F.: Normal modes and boundary layers for a slender tensioned beam on a nonlinear foundation. Nonlinear Dyn. 25(1–3), 79–93 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  27. Vakakis, A.F., Gendelman, O.V., Bergman, L.A., McFarland, D.M., Kerschen, G., Lee, Y.S.: Nonlinear targeted energy transfer in mechanical and structural systems, vol. I and II. Springer, Dordrecht (2008)

    MATH  Google Scholar 

  28. Shaw, S.W., Pierre, C., Pesheck, E.: Modal analysis-based reduced-order models for nonlinear structures-an invariant manifold approach. Shock Vib. Dig. 31(1), 3–16 (1999)

    Article  Google Scholar 

  29. Apiwattanalunggarn, P., Shaw, S.W., Pierre, C., Jiang, D.: Finite element-based nonlinear modal reduction of a rotating beam with large-amplitude motion. J. Vib. Control 9(3–4), 235–263 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  30. Nayfeh, A.H.: Reduced-order models of weakly non-linear spatially continuous systems. Nonlinear Dyn. 16(2), 105–125 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  31. Steindl, A., Troger, H.: Methods for dimension reduction and their applications in nonlinear dynamics. Int. J. Solids Struct. 38(10–13), 2131–2147 (2001)

    Article  MATH  Google Scholar 

  32. Touzé, C., Thomas, O., Chaigne, A.: Hardening/softening behaviour in non-linear oscillations of structural systems using non-linear normal modes. J. Sound Vib. 273(1–2), 77–101 (2004)

    Article  Google Scholar 

  33. Amabili, M., Touzé, C.: Reduced-order models for non-linear vibrations of fluid-filled circular cylindrical shells: comparison of POD and asymptotic non-linear normal modes methods. J. Fluids Struct. 23(6), 885–903 (2007)

    Article  Google Scholar 

  34. Neild, S.A., Wagg, D.J.: Applying the method of normal forms to second-order nonlinear vibration problems. Proc. R. Soc. A 467(2128), 1141–1163 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  35. Haddow, A.G., Barr, A.D.S., Mook, D.T.: Theoretical and experimental study of modal interaction in a two-degree-of-freedom structure. J. Sound Vib. 97(3), 451–473 (1984)

    Article  MathSciNet  Google Scholar 

  36. Nayfeh, A.H., Balachandran, B.: Modal interactions in dynamical and structural systems. ASME Appl. Mech. Rev. 42(11S), 175–201 (1989)

    Article  MathSciNet  Google Scholar 

  37. Yamamoto, T., Yasuda, K.: On the internal resonance in a non-linear two-degree-of-freedom system. Bull. JSME. 20(140), 168–175 (1977)

    Article  MathSciNet  Google Scholar 

  38. Luongo, A., Paolone, A., Di Egidio, A.: Multiple timescales analysis for 1:2 and 1:3 resonant Hopf bifurcations. Nonlinear Dyn. 34(3), 269–291 (2003)

    Article  MATH  Google Scholar 

  39. Luongo, A., Zulli, D., Piccardo, G.: Analytical and numerical approaches to nonlinear galloping of internally resonant suspended cables. J. Sound Vib. 315(3), 375–393 (2008)

    Article  Google Scholar 

  40. Nayfeh, A.H., Mook, D.T.: Nonlinear Oscillations. Willey, New York (1979)

    MATH  Google Scholar 

  41. Nayfeh, A.H., Lacarbonara, W., Chin, C.M.: Nonlinear normal modes of buckled beams: three-to-one and one-to-one internal resonances. Nonlinear Dyn. 18(3), 253–273 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  42. Li, X.Y., Chen, Y.S., Wu, Z.Q.: Non-linear normal modes and their bifurcation of a class of systems with three double of pure imaginary roots and dual internal resonances. Int. J. Non-Linear Mech. 39(2), 189–199 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  43. Monteil, M., Touzé, C., Thomas, O., Benacchio, S.: Nonlinear forced vibrations of thin structures with tuned eigenfrequencies: the cases of 1:2:4 and 1:2:2 internal resonances. Nonlinear Dyn. 75(1–2), 175–200 (2014)

    Article  MATH  Google Scholar 

  44. Srinil, N., Rega, G.: Two-to-one resonant multi-modal dynamics of horizontal/inclined cables, Part II: internal resonance activation, reduced-order models and nonlinear normal modes. Nonlinear Dyn. 48(3), 253–274 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  45. Lee, C., Perkins, N.C.: Three-dimensional oscillations of suspended cables involving simultaneous internal resonances. Nonlinear Dyn. 8(1), 45–63 (1995)

    MathSciNet  Google Scholar 

  46. Amabili, M., Pellicano, F., Valakis, A.F.: Nonlinear vibrations and multiple resonances of fluid-filled, circular shells, Part 1: equations of motion and numerical results. ASME J. Vib. Acoust. 122(4), 346–354 (2000)

    Article  Google Scholar 

  47. Thomas, O., Touzé, C., Chaigne, A.: Non-linear vibrations of free-edge thin spherical shells: modal interaction rules and 1:1:2 internal resonance. Int. J. Solids Struct. 42(11–12), 3339–3373 (2005)

    Article  MATH  Google Scholar 

  48. Mamandi, A., Kargarnovin, M.H., Farsi, S.: Dynamic analysis of a simply supported beam resting on a nonlinear elastic foundation under compressive axial load using nonlinear normal modes techniques under three-to-one internal resonance condition. Nonlinear Dyn. 70(2), 1147–1172 (2012)

    Article  MathSciNet  Google Scholar 

  49. Kerschen, G., Peeters, M., Golinval, J.C., Vakakis, A.F.: Nonlinear normal modes, Part I: a useful framework for the structural dynamicist. Mech. Syst. Signal Process. 23(1), 170–194 (2009)

    Article  Google Scholar 

  50. Peeters, M., Viguié, R., Sérandour, G., Kerschen, G., Golinval, J.C.: Nonlinear normal modes, Part II: toward a practical computation using numerical continuation techniques. Mech. Syst. Signal Process. 23(1), 195–216 (2009)

  51. Pierre, C.: Mode localization and loci veering phenomena in disordered structures. J. Sound Vib. 126(3), 485–502 (1988)

    Article  Google Scholar 

  52. Chan, H.C., Liu, J.K.: Mode localization and frequency loci veering in disordered engineering structures. Chaos Solitons Fractals 11(10), 1493–1504 (2000)

    Article  MATH  Google Scholar 

  53. Kundu, C.K., Han, J.H.: Vibration characteristics and snapping behavior of hygro-thermo-elastic composite doubly curved shells. Compos. Struct. 91(3), 306–317 (2009)

    Article  Google Scholar 

  54. Narakorn, S., Rega, G., Chucheepsakul, S.: Large amplitude three-dimensional free vibrations of inclined sagged elastic cables. Nonlinear Dyn. 33(2), 129–154 (2003)

    Article  MATH  Google Scholar 

  55. Hasheminejad, S.M., Khaani, H.A., Shakeri, R.: Free vibration and dynamic response of a fluid-coupled double elliptical plate system using Mathieu functions. Int. J. Mech. Sci. 75, 66–79 (2013)

    Article  Google Scholar 

  56. Al-Qaisia, A.A., Hamdan, M.N.: On nonlinear frequency veering and mode localization of a beam with geometric imperfection resting on elastic foundation. J. Sound Vib. 332(19), 4641–4655 (2013)

    Article  Google Scholar 

  57. Yi, Z.P., Wang, L.H., Kang, H.J., Tu, G.Y.: Modal interaction activations and nonlinear dynamic response of shallow arch with both ends vertically elastically constrained for two-to-one internal resonance. J. Sound Vib. 333(21), 5511–5524 (2014)

    Article  Google Scholar 

Download references

Acknowledgments

The authors gratefully acknowledge the support given to this research by the National Natural Science Foundation of China (Nos. 11002030, 11032004 and 51178059). Valuable comments and useful suggestions by two anonymous reviewers are also gratefully acknowledged.

Author information

Authors and Affiliations

  1. School of Civil Engineering and Architecture, Changsha University of Science and Technology, Changsha, 410114, People’s Republic of China

    Zhuangpeng Yi

  2. Department of Civil and Environmental Engineering, Rice University, Houston, TX, 77005, USA

    Ilinca Stanciulescu

Authors
  1. Zhuangpeng Yi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ilinca Stanciulescu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhuangpeng Yi.

Appendix

Appendix

$$\begin{aligned} g_1(x)= & {} b\pi \phi ''_m \int _0^1 \phi '_m \sin {2\pi x} \text {d}x \nonumber \\&+\,b\pi ^2\cos 2\pi x\int _0^1(\phi '_m)^2 \text {d}x, \end{aligned}$$
(39)
$$\begin{aligned} g_2(x)= & {} b\pi \phi ''_n \int _0^1 \phi '_n \sin {2\pi x} \text {d}x \nonumber \\&+\,b\pi ^2\cos 2\pi x\int _0^1(\phi '_n)^2 \text {d}x, \end{aligned}$$
(40)
$$\begin{aligned} g_3(x)= & {} b\pi \phi ''_m \int _0^1 \phi '_n \sin 2\pi x \text {d}x \nonumber \\&+\,b\pi \phi ''_n \int _0^1 \phi '_m \sin 2\pi x \text {d}x \nonumber \\&+\,2b\pi ^2 \cos 2\pi x \int _0^1 \phi '_m \phi '_n \text {d}x. \end{aligned}$$
(41)
$$\begin{aligned} \chi _1(x)= & {} b\pi (\varGamma ''_1+2\varGamma ''_2)\int _0^1 \phi '_m \sin 2\pi x\text {d}x \nonumber \\&+\,b\pi \phi ''_m \int _0^1(\varGamma '_1+2\varGamma '_2)\sin 2\pi x\text {d}x \nonumber \\&+\,2b\pi ^2 \cos 2\pi x \int _0^1 \phi '_m (\varGamma '_1+2\varGamma '_2) \text {d}x \nonumber \\&+\,\frac{3}{2}\phi ''_m \int _0^1 (\phi '_m )^2\text {d}x, \end{aligned}$$
(42)
$$\begin{aligned} \chi _2(x)= & {} b\pi (\varGamma ''_5+\varGamma ''_6)\int _0^1 \phi '_n \sin 2\pi x\text {d}x \nonumber \\&+\,b\pi \phi ''_n \int _0^1 (\varGamma '_5+\varGamma '_6) \sin 2\pi x\text {d}x \nonumber \\&+\,\phi ''_m \int _0^1 (\phi '_n)^2 \text {d}x + 2\phi ''_n \int _0^1 \phi '_m \phi '_n \text {d}x \nonumber \\&+\,2b\pi \varGamma ''_4 \int _0^1 \phi '_m \sin 2\pi x\text {d}x \nonumber \\&+\,2b\pi \phi ''_m \int _0^1 \varGamma '_4 \sin 2\pi x\text {d}x \nonumber \\&+\,2b\pi ^2 \cos 2\pi x\int _0^1( 2 \phi '_m \varGamma '_4 \nonumber \\&+\,\phi '_n \varGamma '_5 + \phi '_n \varGamma '_6) \text {d}x, \end{aligned}$$
(43)
$$\begin{aligned} \chi _3(x)= & {} b\pi (\varGamma ''_3+2\varGamma ''_4)\int _0^1 \phi '_n \sin 2\pi x\text {d}x \nonumber \\&+\,b\pi \phi ''_n \int _0^1(\varGamma '_3+2\varGamma '_4)\sin 2\pi x\text {d}x \nonumber \\&+\,2b\pi ^2 \cos 2\pi x \int _0^1 \phi '_n (\varGamma '_3+2\varGamma '_4) \text {d}x \nonumber \\&+\,\frac{3}{2}\phi ''_n \int _0^1 (\phi '_n )^2\text {d}x, \end{aligned}$$
(44)
$$\begin{aligned} \chi _4(x)= & {} b\pi (\varGamma ''_5+\varGamma ''_6)\int _0^1 \phi '_m \sin 2\pi x\text {d}x \nonumber \\&+\,b\pi \phi ''_m \int _0^1 (\varGamma '_5+\varGamma '_6) \sin 2\pi x\text {d}x \nonumber \\&+\,\phi ''_n \int _0^1 (\phi '_m)^2 \text {d}x + 2\phi ''_m \int _0^1 \phi '_m \phi '_n \text {d}x \nonumber \\&+\,2b\pi \varGamma ''_2 \int _0^1 \phi '_n \sin 2\pi x\text {d}x \nonumber \\&+\,2b\pi \phi ''_n \int _0^1 \varGamma '_2 \sin 2\pi x\text {d}x \nonumber \\&+\,2b\pi ^2 \cos 2\pi x\int _0^1( 2 \phi '_n \varGamma '_2 \nonumber \\&+\,\phi '_m \varGamma '_5 + \phi '_m \varGamma '_6) \text {d}x, \end{aligned}$$
(45)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yi, Z., Stanciulescu, I. Nonlinear normal modes of a shallow arch with elastic constraints for two-to-one internal resonances. Nonlinear Dyn 83, 1577–1600 (2016). https://doi.org/10.1007/s11071-015-2432-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-015-2432-3

Keywords

Search

Navigation