Skip to main content
SpringerLink
Log in

The Hopf bifurcation in the Shimizu–Morioka system

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

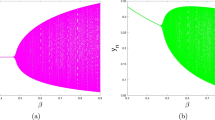
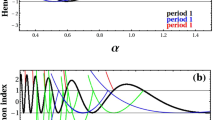
Abstract

We study the local Hopf bifurcations of codimension one and two, which occur in the Shimizu–Morioka system. This system is a simplified model proposed for studying the dynamics of the well-known Lorenz system for large Rayleigh numbers. We present an analytic study and their bifurcation diagrams of these kinds of Hopf bifurcation, showing the qualitative changes in the dynamics of its solutions for different values of the parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Aguirre, L., Arredondo, J.H., López, R., Seibert, P.: On certain generalizations of the Hopf bifurcation. Ann. Mat. Pura Appl. 186, 509–524 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  2. Bibikov, Y.: Local Theory of Nonlinear Analytic Ordinary Differential Equations. Lecture Notes in Mathematics, vol. 702. Springer, New York (1979)

    Google Scholar 

  3. Dias, F.S., Mello, L.F., Zhang, J.-G.: Nonlinear analysis in a Lorenz-like system. Nonlinear Anal. Real World Appl. 11(5), 3491–3500 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  4. Edneral, V., Mahdi, A., Romanovski, V.G., Shafer, D.S.: The center problem on a center mani-fold. Nonlinear Anal. Theory Methods Appl. 75, 2614–2622 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  5. Islam, N., Mazumdar, H.P., Das, A.: On the stability and control of the Schimizu–Morioka system of dynamical equations. Differ. Geom. Dyn. Syst. 11, 135–143 (2009)

    MATH  MathSciNet  Google Scholar 

  6. Kokubu, H., Roussarie, R.: Existence of a singularly degenerate heteroclinic cycle in the Lorenz system and its dynamical consequences: part I. J. Dyn. Differ. Equ. 16(2), 513–557 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  7. Kuznetsov, Y.A.: Elements of Applied Bifurcation Theory. Springer, New York (2004)

    Book  MATH  Google Scholar 

  8. Kuznetsov, Y.A.: Numerical normalization techniques for all codim 2 bifurcations of equilibria in ODE’s. SIAM J. Numer. Anal. 36, 1104–1124 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  9. Lorenz, E.N.: Deterministic nonperiodic flow. J. Atmos. Sci. 20, 130–141 (1963)

    Article  Google Scholar 

  10. Mahdi, A.: Center problem for third-order ODEs. Int. J. Bifurc. Chaos Appl. Sci. Eng. 23(5), 11 (2013)

    MathSciNet  Google Scholar 

  11. Mahdi, A., Romanovski, V.G., Shafer, D.S.: Stability and periodic oscillations in the Moon–Rand systems. Nonlinear Anal. Real World Appl. 14(1), 294–313 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  12. Mello, L.F., Messias, M., Braga, D.C.: Bifurcation analysis of a new Lorenz-like chaotic system. Chaos Solitons Fractals 37, 1244–1255 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  13. Messias, M., Gouveia, M.R.A., Pessoa, C.: Dynamics at infinity and other global dynamical aspects of Shimizu-Morioka equations. Nonlinear Dyn. 69, 577–587 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  14. Pontryagin, L.S.: Ordinary Differential Equations. Addison-Wesley, Reading (1962)

    MATH  Google Scholar 

  15. Romanovski, V.G., Shafer, D.S.: The Center and Cyclicity Problems: A Computational Algebra Approach. Birkhäuser, Boston (2009)

    Google Scholar 

  16. Rubinger, R.M., Nascimento, A.W.M., Mello, L.F., Rubinger, C.P.L., Manzanares Filho N., Albuquerque, H.A.: Inductorless Chua’s circuit: experimental time series analysis. Math. Probl. Eng. 2007 (2007). doi:10.1155/2007/83893

  17. Shilnikov, A.L.: On bifurcations of the Lorenz attractor in the Shimizu–Morioka model. Phys. D Nonlinear Phenom. 62, 338–346 (1993)

    Article  MathSciNet  Google Scholar 

  18. Shimizu, T., Morioka, N.: On the bifurcation of a symmetric limit cycle to an asymmetric one in a simple model. Phys. Lett. A 76(3,4), 201–204 (1980)

  19. Takens, F.: Unfoldings of certain singularities of vectorfields: Generalized Hopf bifurcations. J. Differ. Equ. 14, 476–493 (1973)

    Article  MATH  MathSciNet  Google Scholar 

  20. Tigan, G., Turaev, D.: Analytical search for homoclinic bifurcations in the Shimizu-Morioka model. Phys. D Nonlinear Phenom. 240(12), 985–989 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  21. Vladimirov, A.G., Volkov, D.Y.: Low-intensity chaotic operations of a laser with a saturable absorber. Opt. Commun. 100, 351–360 (1993)

    Article  Google Scholar 

  22. Yu, S., Tang, W.K.S., Lü, J., Chen, G.: Generation of \(n\times m\)-wing Lorenz-like attractors from a modified Shimizu–Morioka model. IEEE Trans. Circuit Syst. 55(11), 1168–1172 (2008)

    Article  Google Scholar 

Download references

Acknowledgments

The first author was partially supported by the Grants MINECO/FEDER MTM 2008-03437, AGAUR 2014SGR 568, ICREA Academia and FP7 PEOPLE-2012-IRSES-316338 and 318999. The second author was partially supported by Program CAPES/DGU Process 8333/13-0 and by FAPESP Project 2011/13152-8.

Author information

Authors and Affiliations

  1. Departaments de Matematiques, Universitat Autònoma de Barcelona, 08193, Bellaterra, Barcelona, Catalonia, Spain

    Jaume Llibre

  2. Departamento de Matemática, Universidade Estadual Paulista, Campus de São José do Rio Preto - IBILCE, R. Cristóvão Colombo, 2265, São José do Rio Preto, SP, 15.054000, Brazil

    Claudio Pessoa

Authors
  1. Jaume Llibre
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Claudio Pessoa
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Claudio Pessoa.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Llibre, J., Pessoa, C. The Hopf bifurcation in the Shimizu–Morioka system. Nonlinear Dyn 79, 2197–2205 (2015). https://doi.org/10.1007/s11071-014-1805-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-014-1805-3

Keywords

Mathematics Subject Classification

Search

Navigation