Invariant subspace reduction for linear dynamic analysis of finite-dimensional viscoelastic structures

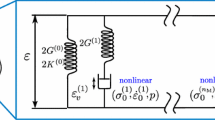
Abstract

The linear dynamics of finite-dimensional viscoelastic structures is addressed in this paper. The equations of motion of a general, discrete or discretized, dynamical system, made of elements behaving as multiparameter viscoelastic solid models, are formulated in terms of internal variables, whose evolution is ruled by flow laws. The classical elastic-viscoelastic Principle of Correspondence is discussed in conjunction with the Fourier transform, and a new strategy, which leaves the system in the time-domain is proposed. By exploiting the fact that the spectrum of the system is well-separated if damping is small, a Center Manifold-like reduction is performed, which eliminates the internal variables, lowering the dimensions to those of the corresponding elastic system, thus filtering the fast dynamics. The order of magnitude of the error related to the reduction is investigated. A comparison with the popular Kelvin–Voigt model is performed for homogeneous structures. Examples on sample structures are worked out, namely the one degree-of-freedom viscoelastic system and the discretized elastic beam on viscoelastic soil. In all the examples the (3-Parameters) Standard Model is adopted.

Appendix: Free dynamics of the Standard Model viscoelastic oscillator for medium or large viscosity coefficients

This "Appendix" is devoted to furnish some detail on how the free dynamics of the SO changes when medium or large viscosity coefficient are considered.

Fig. 11

Exact versus asymptotic moduli of the eigenvalues of the SO when b varies: a real parts; b imaginary part. $c_{0}=15, c_{v}=5$

The discussion is developed by referring, first, to the graphs displayed in Fig. 11, where the moduli of both the exact roots of Eq. (44) (gray curves), and the asymptotic roots (black curves), furnished by Eq. (45), are plotted vs b, when $c_{0}=15, c_{v}=5$; in particular, Fig. 11a is relevant to the moduli of the real part of the eigenvalues $\left| \mathrm {Re}\left( \lambda _{1}\right) \right| , \left| \mathrm {Re}\left( \lambda _{2}\right) \right|$, respectively, while in Fig. 11b the modulus of the imaginary part $\left| \mathrm {Im}\left( \lambda _{2}\right) \right|$ is shown. It is found that, when b increases from zero, while $\left| \mathrm {Re}\left( \lambda _{1}\right) \right|$ monotonically decreases (Fig. 11a), i.e. the real negative root moves towards the imaginary axis, $\left| \mathrm {Re}\left( \lambda _{2}\right) \right|$ first grows with b, reaching a maximum at $b=4.13=:b_{opt}$ (exact solution), and then it decreases, that is the complex eigenvalues first move away from the imaginary axis and then come back towards it. Since the damping coefficient of the oscillatory decaying part of the response is proportional to $\left| \mathrm {Re}\left( \lambda _{2}\right) \right|$, then $b_{opt}$ represents an optimum value of the viscosity coefficient, which maximizes the damping. Moreover, the two curves $\left| \mathrm {Re}\left( \lambda _{1}\right) \right| , \left| \mathrm {Re}\left( \lambda _{2}\right) \right|$ cross each other at $b=4.86=:b_{cr}$ (exact solution), thus entailing that, increasing the viscosity coefficient produces a change of the character of the decaying motion, namely: if $b<b_{cr}$ the exponential decaying part of the motion is faster than the oscillatory one, otherwise, if $b>b_{cr}$ it is slower than the oscillatory one. In addition, with reference to (Fig. 11b), as b overcomes a threshold, a not negligible dependence of the (exact) frequency $\left| \mathrm {Im}\left( \lambda _{2}\right) \right|$ on the viscosity coefficient is recognized. As a final comment, the asymptotic solutions of Eq. (45), as it is expected, lose their validity when b is not small and becomes larger than a certain value, i.e. the black curves of Fig. 11a, b leave the gray ones.

Fig. 12

SO free dynamics when $b=4.13$ in sub-figures (a), (b), and when $b=200$ in sub-figures (c), (d): a, c eigenvalues; b, d orbits. $c_{0}=15, c_{v}=5, u(0)=-0.1, v(0)=0.03, w(0)=0.2$

The above mentioned qualitative responses of the SO, relevant to medium or large viscosity coefficients b, are sketched in Fig. 12 where, for the same values of $c_{0}, c_{v}$ and for the same initial conditions adopted in Sect. 6.1, the spectra of the eigenvalues and the free motion-orbits in the state-space, are shown when $b=b_{opt}$ (Fig. 12a, b), and when $b=200$ (Fig. 12c, d).

When $b=b_{opt}$ (Fig. 12a, b), it is seen that: (1) the spectrum of eigenvalues (gray circles in Fig. 12a) is not well-separated, i.e. $\left| \mathrm {Re}\left( \lambda _{1}\right) \right|$ is of the same order of $\left| \mathrm {Re}\left( \lambda _{2}\right) \right|$; (2) since $\left| \mathrm {Re}\left( \lambda _{1}\right) \right| >\left| \mathrm {Re}\left( \lambda _{2}\right) \right|$ the exponential character of the motion has a faster in-time decaying with respect to the oscillatory one; (3) since $\left| \mathrm {Re}\left( \lambda _{2}\right) \right|$ is maximized by $b_{opt}$ the in-time decaying of the oscillations is faster with respect to the case of small viscosity coefficient. These latter considerations are corroborated by the plot of Fig. 12b, where the orbit in the state-space is shown: the free motion develops itself along a spiral trajectory, wrapped around the one-dimensional subspace $r:=\mathrm {Span}\left[ \mathbf {u}_{1}\right]$; differently from the small viscosity-case, the two phases of the motion cannot be distinguished, namely a part of the trajectory is not more parallel to r (remember that the spectrum of the eigenvalues is not well-separated) and, therefore, there is not a recognizable fast transient motion tending to $\pi :=\mathrm {Span}\left[ \mathrm {Re}\left( \mathbf {u}_{2}\right) ,\mathrm {Im}\left( \mathbf {u}_{2}\right) \right]$. Moreover, as it is expected, when the viscosity coefficient is not small, the effectiveness of the RO in reproducing the dynamical behavior of the SO decreases; e.g., in Fig. 12a, it is apparent that the complex eigenvalues of the RO are quite far from those of the SO.

When b is large (Fig. 12c, d), it is found that: (1) the spectrum of eigenvalues (Fig. 12c) is not well-separated; (2) since $\left| \mathrm {Re}\left( \lambda _{1}\right) \right| <\left| \mathrm {Re}\left( \lambda _{2}\right) \right|$ the exponential character of the motion has a slower in-time decaying with respect to the oscillatory one; (3) $\left| \mathrm {Re}\left( \lambda _{2}\right) \right|$ is about an order of magnitude smaller with respect to that of the small viscosity-case, thus implying that the in-time decaying of the oscillations is very slow; (4) since $\left| \mathrm {Re}\left( \lambda _{1}\right) \right|$ is about two orders of magnitude smaller with respect to that of the small viscosity-case, also the in-time decaying of the exponential component of the motion is very slow. The orbit in the state-space, shown in Fig. 12d, confirms these considerations: indeed, the spiral trajectory, is wrapped around the one-dimensional subspace r, as it occurs in the previous cases, but it is able to reach the plane $\pi$ only after several elliptical orbits, which are almost parallel to $\pi$ are experienced; remarkably, this kind of dynamics reflects the slow in-time decaying of both exponential and oscillatory components of motion.

In conclusion, when b is not small, the SO does not more behave as a one d.o.f. system, the displacements u and w are not more in-phase, and, depending on the magnitude of the viscous coefficient, an highly damped response (Fig. 12b), as well as a weakly damped motion, in which the mass experiences larger in-time oscillations with respect to the Kelvin–Voigt element (Fig. 12d), are possible.