Dynamic instability of coupled nanobeam systems

Abstract

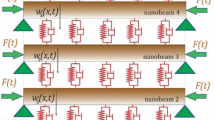
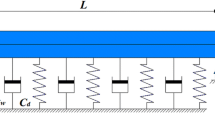
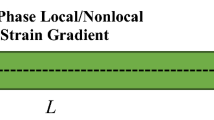
The dynamic instability problem of coupled nanobeam system subjected to compressive axial loading is investigated. The paper is concerned with the stochastic parametric vibrations of nanobeams based on Eringen’s nonlocal elasticity theory of Helmholtz and bi-Helmholtz type of kernel and Euler–Bernoulli beam theory. Each pair of axial forces consists of a constant part and a time-dependent stochastic function. By using the direct Liapunov method, bounds of the almost sure asymptotic instability of a coupled nanobeam system as a function of viscous damping coefficient, stiffness of the coupling elastic medium, variances of the stochastic forces, scale coefficients, and intensity of the deterministic components of axial loading are obtained. Analytical results are verified with the numerical results obtained from the Monte Carlo simulation. Numerical calculations are performed for the Gaussian process with a zero mean as well as a harmonic process with random phase.

Appendices

Appendix 1

Assuming that

$$f_{o1} < \frac{{\alpha_{m}^{2} }}{{{{\mathscr{L}}}_{m} }} + \frac{K}{{\alpha_{m}^{2} }},\quad f_{o2} < \frac{{\alpha_{m}^{2} }}{{{{\mathscr{L}}}_{m} }} + \frac{K}{{\alpha_{m}^{2} }},$$

(59)

which implies the condition that the beams, separated and lying on the elastic layer, are statically stable. For the Helmholtz kernel, the right sides of relations (59) are equivalent with relation (40) in Murmu and Adhikari [17]. Relation (34) is fulfilled if:

$$f_{o1} f_{o2} - \left( {\frac{{\alpha_{m}^{2} }}{{{{\mathscr{L}}}_{m} }} + \frac{K}{{\alpha_{m}^{2} }}} \right)(f_{o1} + f_{o2} ) + \left( {\frac{{\alpha_{m}^{2} }}{{{{\mathscr{L}}}_{m} }} + \frac{K}{{\alpha_{m}^{2} }}} \right)^{2} - \frac{K}{{\alpha_{m}^{4} }} \ge 0.$$

(60)

By introducing the ratio of the axial load χ = f _o2/f _o1, from relation (60) one obtains

$$f_{o1(1,2)} = \frac{{(1 + \chi )\left( {\frac{{\alpha_{m}^{2} }}{{{{\mathscr{L}}}_{m} }} + \frac{K}{{\alpha_{m}^{2} }}} \right) \mp \sqrt {(1 + \chi )^{2} \left( {\frac{{\alpha_{m}^{2} }}{{{{\mathscr{L}}}_{m} }} + \frac{K}{{\alpha_{m}^{2} }}} \right) + 4\chi K^{2} } }}{2\chi }.$$

(61)

For χ = 1, buckling loads obtained from relations (61) are equivalent with relations (36) and (37) obtained by Murmu and Adhikari [17].The critical buckling load is

$$f_{o1}^{cr} = \frac{{(1 + \chi )\left( {\frac{{\alpha_{m}^{2} }}{{{{\mathscr{L}}}_{m} }} + \frac{K}{{\alpha_{m}^{2} }}} \right) - \sqrt {(1 - \chi )^{2} \left( {\frac{{\alpha_{m}^{2} }}{{{{\mathscr{L}}}_{m} }} + \frac{K}{{\alpha_{m}^{2} }}} \right)^{2} + 4\chi K^{2} } }}{2\chi }.$$

(62)

Liapunov functional is positive definite if deterministic components of axial loadings are smaller than critical buckling loads, i.e. if static stability conditions (59) and (60) for a double-nanobeam system are satisfied.

Appendix 2

The coefficients in biquadratic Eq. (46)

$$\begin{aligned} b_{0m} = & \, K\left( {2\beta^{2} + 2\frac{{\alpha_{m}^{4} }}{{{{\mathscr{L}}}_{m} }} - f_{o1} \alpha_{m}^{2} - f_{o2} \alpha_{m}^{2} } \right) \\ & + \left( {\beta^{2} + \frac{{\alpha_{m}^{4} }}{{{{\mathscr{L}}}_{m} }} - f_{o1} \alpha_{m}^{2} } \right)\left( {\beta^{2} + \frac{{\alpha_{m}^{4} }}{{{{\mathscr{L}}}_{m} }} - f_{o2} \alpha_{m}^{2} } \right), \\ b_{1m} = & \left( {K + \beta^{2} + \frac{{\alpha_{m}^{4} }}{{{{\mathscr{L}}}_{m} }} - f_{o2} \alpha_{m}^{2} } \right)\left( {2\beta^{2} + \alpha_{m}^{2} f_{1} (t)} \right)^{2} \\ & + \,\left( {K + \beta^{2} + \frac{{\alpha_{m}^{4} }}{{{{\mathscr{L}}}_{m} }} - f_{o1} \alpha_{m}^{2} } \right)\left( {2\beta^{2} + \alpha_{m}^{2} f_{2} (t)} \right)^{2} , \\ b_{2m} = & \left( {2\beta^{2} + \alpha_{m}^{2} f_{1} (t)} \right)^{2} \left( {2\beta^{2} + \alpha_{m}^{2} f_{2} (t)} \right)^{2} . \\ \end{aligned}$$

(63)