An analytical model for the static behaviour of honeycomb sandwich plates with auxetic cores using higher-order shear deformation theories

Abstract

This paper presents an analytical model to investigate the static behaviour of sandwich plates comprised of two isotropic face sheets and a honeycomb core. Through-thickness transverse shear stresses were considered using a unified displacement field with which various plate theories were implemented, i.e., exponential, third-order, hyperbolic, sinusoidal, fifth-order, Mindlin, and the classic plate theory. The equilibrium equations of a simply-supported sandwich panel were derived using the principle of virtual work and Navier solution was obtained under static transverse loading. After validating of the model, various mechanical and geometrical parameters were varied to characterise the behaviour of the structure under regular and auxetic response. It was found that the auxeticity of the core strongly affects the mechanical response, e.g., in controlling deflection, in-plane anisotropy, and Poisson’s ratio. Cell wall angle was found to be most critical parameter that can be used to adjust anisotropy, out-of-plane shear modulus, transverse shear stress distribution, and deflection of the panel. Also the cell aspect ratio controls the sensitivity of the core response to other geometrical variations. In terms of the higher-order theories, the deflection-dependent parameter of the unified formulation seems to have more control of maximum deflection compared to independent rotations. Auxeticity of the core showed some benefits in controlling anisotropy, deflection and providing additional out-of-plane shear rigidity. Overall, since there is not one-to-one relationship between specific values of Poisson’s ratio, anisotropy, and shear rigidity, careful design considerations must be invested to obtain a correct mechanical response.

1 Introduction

Overview. In the recent years, auxetic materials have received a great deal of attention due to their unique performance under mechanical loading (Dhari et al. 2020, 2021). Their exotic behaviour is attributed to the negative values of Poisson’s ratio where a longitudinal compression (or tension) is accompanied by a transverse shrinkage (or expansion). In the classical theory of elasticity, Poisson’s ratio ranges between $-1$ and 0.5 for isotropic media (Mott and Roland 2013) whereas for the anisotropic continua, there are no limits for its values (Ting and Chen 2005). More interestingly and in contrast to full auxeticity, a partial auxetic behaviour is observed at certain directions for crystals with cubic symmetry (Tretiakov et al. 2018; Tretiakov and Wojciechowski 2020), which introduces additional complexity. In the current work, the regular honeycomb structure and its auxetic counterpart—the re-entrant (inverse) honeycomb—is studied as the core of a composite sandwich panel (Hall and Javanbakht 2021).

Honeycomb structures. As one of the oldest bio-inspired patterns, regular honeycomb structures and their re-entrant configuration have been used in a variety of applications such as sports (Duncan et al. 2018; Wang and Hong 2014), bioengineering (Kölbl et al. 2020; Mirzaali et al. 2018), acoustics (Melnikov et al. 2020), and impact resistance (Sethi et al. 2023; Korupolu et al. 2022; Tewari et al. 2022) among others. Programming and tuning the mechanical properties of auxetics allow for a tailored response of these high-performance metamaterials (Yang et al. 2019; Khoshgoftar et al. 2021; Khorshidi et al. 2022). The auxetic property adds additional flavours to the regular material properties such as extreme anisotropy (Dirrenberger et al. 2013) and unboundedness of Poisson’s ratio (Ting and Chen 2005) which extends the design space of structures. Although honeycomb structures have been studied a lot in the literature, characterising their effective behaviour can provide additional insight towards better designs; analytical solutions provide a robust and quick approach to this end.

Modelling auxetic structures. Various analytical and numerical methods have been used in simulating the response of auxetics. In Duc et al. (2017), the dampened dynamic response of double-curved shallow shells were investigated under blast forces. The nonlinear behaviour was formulated based on the Mindlin plate theory (Mindlin 1951) and solved using the Airy stress functions and Galerkin approximation. In Hou et al. (2013), the failure of polymorphic honeycomb were studied using finite element simulations. By gradually modifying the geometrical parameters, the local and global deformation mechanism of polymorphic cores and thus their flexural response can be regulated. In Zhu et al. (2019), the eigen-frequencies of auxetic/regular honeycomb sandwich plates were obtained using the nonlinear von Kármán-type and third-order shear deformation theories. It was found that the auxetic core takes a lower total vibrational energy compared to the regular one. Overall, various combinations of analytical plate theories, numerical simulations, and experimental methods are used to model auxetic honeycombs.

Classic plate theories. Shell-like structures and plates, as their flat counterparts, are manifolds that often has a negligible thickness. Their analysis could take two general pathways; the direct approach (Javanbakht et al. 2019, Aßmus et al. 2023, Zhilin 1976, Pal’mov 1982) or the engineering approach (Timoshenko and Woinowsky-Krieger 1959). In the former, the directed surfaces of generalised continuum mechanics (Altenbach and Eremeyev 2009) are used to set up the required mathematical objects for the definition of a manifold; in the latter, the governing equations are reduced from three-dimensional elasticity onto a plane, see Carrera and Brischetto (2008); Khorshidi and Karimi (2020) for instance.

The engineering approach, in its displacement-based variant, takes the unknown displacements as the primary variable. The simplest plate theory in this sense, is the classical plate theory (Kirchhoff-Love theory or shear-rigid theory) Kirchhoff (1850) which is used for thin plates as it neglects the shear deformations and considers an independent equilibrium for shear stresses (Zienkiewicz and Holister 1965). Consequently, the critical buckling loads and natural frequencies are overestimated by the theory whereas the stress components and deflections are underestimated. The first-order shear deformation theory or Mindlin theory (Mindlin 1951) includes the shear deformations and assumes a constant transverse shear stress through the thickness. Although it addresses the stiffness issue of the classic plate theory, the traction-free boundary conditions are violated at the bottom and top free surfaces, see Rahimi et al. (2012); Khoshgoftar et al. (2015, 2022); Xiang (2002); Khorshidi et al. (2019) for more recent developments. Such shortcomings are tackled by higher-order plate theories.

Higher-order plate theories. Higher-order plate theories can mathematically capture various through-thickness distributions of transverse shear stress and thus can represent cross-sectional warping without using shear correction factors. In the recent years, the development of these theories have attracted interest in the literature (Khorshidi and Karimi 2019; Khorshidi et al. 2020; Mashat et al. 2020; Furtmüller and Adam 2020; Tran Vinh et al. 2016). For example, exponential shear deformation theory (Sayyad and Ghugal 2012) was developed for moderately thick plates, including the impacts of rotary inertia and transverse deflections. It was shown that the precision and reliability of this theory are higher than polynomial shear deformation theories because exponential theories can reduce to polynomial theories by truncating the expanded power series. In some cases, higher order shear deformation theories are not computationally suitable because through-thickness modifications increase the number of unknowns in the displacement field (Pradyumna and Bandyopadhyay 2008; Neves et al. 2012; Talha and Singh 2010). In the context of auxetics, providing a formulation, which incorporates various theories, seems to be an interesting journey to embark.

Motivation. Many higher-order theories have been used to model the mechanical response of regular or auxetic honeycombs. For instance, the linear static response of an auxetic core in a sandwich panel was formulated using a third-order shear theory, which included stress–strain response and a parametric study showing a range of values for Poisson’s ratio (Pham et al. 2020). The classic plate theory was used to obtain natural frequencies of vibration for a regular honeycomb sandwich panel in a parametric study (Jweeg 2016); the effect of changing the wall angle and layer thickness were studied therein. The vibration response of a regular honeycomb cores and composite skin layers was studied under blast loads using a third-order shear deformation theory in Pham et al. (2023). The formulation uses the rule of mixtures (Javanbakht et al. 2020) to obtain the effective properties of layers (Javanbakht et al. 2016) and set up a new finite element for improved accuracy. Most of the literature discusses the results of the auxetic cores using a certain theoretical approach combined with the finite element method. Synthesising these approaches reveal that most of the analytical formulations for honeycombs are based on Gibson’s beam model (Gibson and Ashby 1997) and a plate theory; the results cover static, dynamic, and eigenvalue analysis of vibration. Nevertheless, they all lack a comprehensive modelling that include various theories and a comparison of their performance. Herein, this aspect will be addressed within a theory—that synthesises various plate theories—in addition to a comprehensive analysis of the regular and auxetic behaviour. The success of the approach is demonstrated through a static analysis which can be extended to other types as well.

Aim. Although various theories have been used to simulate the response of auxetics, a uniform formulation has not been provided for sandwich panels with auxetic honeycomb cores. Thus, it is aimed to provide an analytical solution for sandwich panels with regular and re-entrant honeycomb cores, which encompass various higher-order shear theories. The solutions will help to compare the response of the sandwich panel in regular and auxetic modes and its affecting parameters such as vertical cell rib length, inclined cell rib length, and cell wall angle. The provided formulation can be used as a design roadmap for such structures. In the following sections, a unified higher-order plate formulation is developed for a general honeycomb structure; after validating the results with a finite element model and benchmark values in the literature, parametric analyses on the core properties and the sandwich panel were conducted. After discussing the results, the study concludes by highlighting the key findings.

2 Formulation

2.1 Physical geometry of the model

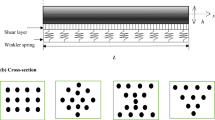
A sandwich structure subjected to static loading, consisting of an auxetic core and two isotropic facesheets is assumed. The width, length, total thickness, and effective density (Bergmann et al. 2020) of the structure are denoted by b, a, h, and $\rho$, respectively; the thickness of the core and each facesheet, are denoted by $t_{c}$, $t_{f}$, respectively. A right-handed frame of reference is placed at the corner of the sandwich plate, where $x_1$–$x_2$ axes span the structural plane, see Fig. 1. The unit cell of the auxetic core is shown in Fig. 1b, where the geometrical parameters $l_{1}$, $l_{2}$ and $\theta$ denote the length of the inclined rib, horizontal length of the cell, and cell wall angle, respectively. Note that a positive angle characterises a re-entrant/inverted honeycomb whereas regular honeycombs are obtained from negative angles, e.g., $l_1=l_2$, $t_1=t_2$, and $\theta =-30$ result in regular hexagonal honeycombs. Additionally, the aspect ratio ($\eta _1$), thickness ratio ($\eta _{2}$), and the thickness-to-length ratio ($\eta _3$) of the cell are defined as

$$\begin{aligned} \eta _1\mathrel {:=}&\;\frac{l_2}{l_1}, \end{aligned}$$

(1a)

$$\begin{aligned} \eta _2\mathrel {:=}&\;\frac{t_2}{t_1}, \end{aligned}$$

(1b)

$$\begin{aligned} \eta _3\mathrel {:=}&\;\frac{t_1}{l_1}. \end{aligned}$$

(1c)

Fig. 1

Schematic of the hexagonal honeycomb core embedded in a sandwich panel: a Geometry of a sandwich panel, b the unit cell of hexagonal honeycomb core, and c three-dimensional layout of the honeycomb panel

2.2 Kinematics of higher-order shear deformation theories

In contrast to the first-order shear deformation theory, higher-order shear deformation theories are needless of shear correction factor as their transverse shear stresses automatically vanish at the top and bottom surfaces of the plate. Based on these theories, a general description of the displacement field is assumed to be

$$\begin{aligned} {{u}_{1}}&\mathrel {:=}u+g w_{,1}+f\zeta , \end{aligned}$$

(2a)

$$\begin{aligned} {{u}_{2}}&\mathrel {:=}v+g w_{,2}+f\psi , \end{aligned}$$

(2b)

$$\begin{aligned} {{u}_{3}}&\mathrel {:=}w, \end{aligned}$$

(2c)

where $u_1\equiv u_1\left( x_1,x_2,x_3 \right)$, $u_2\equiv u_2\left( x_1,x_2,x_3 \right)$ and $u_3\equiv \left( x_1,x_2,x_3 \right)$ express the displacement of an arbitrary point in the $x_1$, $x_2$ and $x_3$ directions, respectively. The mid-plane displacement components of the sandwich panel are expressed in terms of the planar coordinates, i.e., $u\equiv u(x_1,x_2)$, $v\equiv v(x_1,x_2)$ and $w\equiv w(x_1,x_2)$ along the x-, y-, and z-axes, respectively. Moreover, independent rotation angles caused by bending about the y- and $x_1$- axes are defined by $\zeta (x_1,y_1)$ and $\psi (x_1,y_1)$, respectively. Depending on the adopted theory, specific continuous functions are used for $g\equiv g(x_3)$ and $f\equiv f(x_3)$ which assign different weights to the deflection-dependent and independent rotations of the plate, respectively. In consequence, a specific through-thickness distribution of stress is obtained for the transverse shear stress, see Table 1 for an overview.

Table 1 A unified overview of various plate theories in terms of two general continuous functions

.

2.3 Compatibility equations and constitutive relations

Within the elastic regime, the infinitesimal strain field can be deduced from Eq. (2):

$$\begin{aligned} {{\varepsilon }_{11}}&=u_{,1}+gw_{,11}+f\zeta _{,1}, \end{aligned}$$

(3a)

$$\begin{aligned} {{\varepsilon }_{22}}&=v_{,2}+gw_{,22}+f\psi _{,2}, \end{aligned}$$

(3b)

$$\begin{aligned} {{\varepsilon }_{12}}&={1}/{2}\left[ u_{,2} + v_{,1} + 2gw_{,12} + f\left( \psi _{,1} + \zeta _{,2}\right) \right] , \end{aligned}$$

(3c)

$$\begin{aligned} {{\varepsilon }_{13}}&={1}/{2}\left[ g_{,3}w_{,1} + \zeta f_{,3} + w_{,1} \right] , \end{aligned}$$

(3d)

$$\begin{aligned} {\varepsilon }_{23}&={1}/{2}\left[ g_{,3}w_{,2} + \psi f_{,3} + w_{,2} \right] . \end{aligned}$$

(3e)

The constitutive equations for the considered sandwich plate are expressed using the generalised Hooke’s law:

$$\begin{aligned} {{ \begin{Bmatrix} {{\sigma }_{11}} \\ {{\sigma }_{22}} \\ {{\sigma }_{23}} \\ {{\sigma }_{13}} \\ {{\sigma }_{12}} \\ \end{Bmatrix}}^{\left[ i \right] }} ={{ \begin{bmatrix} {{Q}_{11}} &{} {{Q}_{12}} &{} 0 &{} 0 &{} 0 \\ {{Q}_{21}} &{} {{Q}_{22}} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} {{Q}_{44}} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} {{Q}_{55}} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} {{Q}_{66}} \\ \end{bmatrix} }^{\left[ i \right] }} \begin{Bmatrix} {{\varepsilon }_{11}} \\ {{\varepsilon }_{22}} \\ {{\varepsilon }_{23}} \\ {{\varepsilon }_{13}} \\ {{\varepsilon }_{12}} \\ \end{Bmatrix} \qquad \qquad \forall i\in \big \{1,2,3\big \}, \end{aligned}$$

(4)

where the properties of the i-th layer are marked by the superscript [i], i.e., the bottom facesheet ([1]), core ([2]), and the top facesheet/skin ([3]); moreover, the stiffness coefficients ($Q_{ij}$) are

$$\begin{aligned} Q_{11}^{\left[ i \right] }&=\frac{E_{1}^{\left[ i \right] }}{1-\nu _{12}^{\left[ i \right] }\nu _{21}^{\left[ i \right] }}, \end{aligned}$$

(5a)

$$\begin{aligned} Q_{22}^{\left[ i \right] }&=\frac{E_{2}^{\left[ i \right] }}{1-\nu _{12}^{\left[ i \right] }\nu _{21}^{\left[ i \right] }}, \end{aligned}$$

(5b)

$$\begin{aligned} Q_{12}^{\left[ i \right] }&=Q_{21}^{\left[ i \right] }=\frac{E_{2}^{\left[ i \right] }\nu _{12}^{\left[ i \right] }}{1-\nu _{12}^{\left[ i \right] }\nu _{21}^{\left[ i \right] }}, \end{aligned}$$

(5c)

$$\begin{aligned} Q_{44}^{\left[ i \right] }&=G_{23}^{\left[ i \right] }, \end{aligned}$$

(5d)

$$\begin{aligned} Q_{55}^{\left[ i \right] }&=G_{13}^{\left[ i \right] }, \end{aligned}$$

(5e)

$$\begin{aligned} Q_{66}^{\left[ i \right] }&=G_{12}^{\left[ i \right] }, \end{aligned}$$

(5f)

where $G_{13}^{\left[ i \right] },~G_{23}^{\left[ i \right] },~G_{12}^{\left[ i \right] },~E_{1}^{\left[ i \right] },E_{2}^{\left[ i \right] },\nu _{12}^{\left[ i \right] }$ and $\nu _{21}^{\left[ i \right] }$ are shear elastic modulus, Young’s modulus and Poisson’s ratios, respectively. For the isotropic face sheets ($i=1,3$), the stiffness coefficients in Eq. (5) reduce to

$$\begin{aligned} \forall i\in \big \{1,3\big \}:\left\{ \begin{array}{ll} Q_{11}^{\left[ i \right] }&{}=Q_{22}^{\left[ i \right] }=\frac{E}{1-{{\nu }^{2}}},\\ Q_{12}^{\left[ i \right] }&{}=Q_{21}^{\left[ i \right] }=\frac{E\nu }{1-{{\nu }^{2}}},\\ Q_{44}^{\left[ i \right] }&{}=Q_{55}^{\left[ i \right] }=Q_{66}^{\left[ i \right] }=G=\frac{E~}{2\left( 1+\nu \right) }, \end{array}\right. \end{aligned}$$

(6)

where $E\equiv E^{[1]}\equiv E^{[3]}$, $\equiv G^{[1]}\equiv G^{[3]}$ and $\nu \equiv \nu ^{[1]}\equiv \nu ^{[3]}$ denote the Young’s modulus, shear modulus and Poisson’s ratio of the symmetric isotropic face sheets, respectively. For the auxetic core with the assumed honeycomb cells, the extended Gibson’s formulation is readily obtained (Zhu et al. 2019):

$$\begin{aligned} E_{1}^{\left[ 2 \right] }&=E\frac{\eta _{3}^{3}\sec ^3\theta \left( {{\eta }_{1}}-\sin \theta \right) }{\eta _{3}^{2}\left( {{\eta }_{1}}\sec ^2\theta +\tan ^2\theta \right) +1}, \end{aligned}$$

(7a)

$$\begin{aligned} E_{2}^{\left[ 2 \right] }&=E\frac{\eta _{3}^{3}\sec \theta }{\left( {{\eta }_{1}}-\sin \theta \right) \left( \eta _{3}^{2}+\tan ^2\theta \right) }, \end{aligned}$$

(7b)

$$\begin{aligned} G_{12}^{\left[ 2 \right] }&=E\frac{\eta _{3}^{3}\sec \theta }{{{\eta }_{1}}\left( 2{{\eta }_{1}}+1 \right) }, \end{aligned}$$

(7c)

$$\begin{aligned} G_{23}^{\left[ 2 \right] }&=G\frac{{{\eta }_{3}}\cos \theta }{{{\eta }_{1}}-\sin \theta }, \end{aligned}$$

(7d)

$$\begin{aligned} G_{31}^{\left[ 2 \right] }&=\frac{1}{2}G{{\eta }_{3}}\sec \theta \left( \frac{{{\eta }_{1}}+2\sin \theta }{2\left( {{\eta }_{1}}-\sin \theta \right) }+\frac{{{\eta }_{1}}-\sin \theta }{2{{\eta }_{1}}+1} \right) , \end{aligned}$$

(7e)

$$\begin{aligned} \nu _{12}^{\left[ 2 \right] }&=-\frac{\left( 1-\eta _{3}^{2} \right) \tan \theta \sec \theta \left( {{\eta }_{1}}-\sin \theta \right) }{\eta _{3}^{2}\left( \frac{\eta _1}{\eta _2} \sec ^2\theta +\tan ^2\theta \right) +1}, \end{aligned}$$

(7f)

$$\begin{aligned} \nu _{21}^{\left[ 2 \right] }&=-\frac{\left( 1-\eta _{3}^{2} \right) \sin \theta }{\left( {{\eta }_{1}}-\sin \theta \right) \left( \eta _{3}^{2}+\tan ^2\theta \right) }, \end{aligned}$$

(7g)

$$\begin{aligned} {{\rho }^{\left[ 2 \right] }}&=\rho \frac{\left( {{\eta }_{1}\eta _2}+2 \right) {{\eta }_{3}}\sec \theta }{2\left( {{\eta }_{1}}-\sin \theta \right) }, \end{aligned}$$

(7h)

where the dimensionless geometrical parameters of the cell, i.e., $\eta _1$, $\eta _2$, and $\eta _3$, are involved. Note that $\eta _{2}$ is included in (7f) and (7h) and thus for simplicity, a unit value is assumed for this ratio.

2.4 Equilibrium equations

To derive the governing equations and related boundary conditions of the system, virtual work principle is applied as follows

$$\begin{aligned} \int _{0}^{t}\left( \delta V+\delta U \right) {{\,\mathrm{d\!}\,}}t=0, \end{aligned}$$

(8)

where the strain energy of the sandwich plate U and work done by applied forces V are calculated as

$$\begin{aligned} \delta U&=\frac{1}{2}\underset{i=1}{\overset{3}{\mathop \sum }}\,\underset{{{\mathscr {V} }^{\left[ i \right] }}}{\overset{{}}{\mathop \int }}\, \left ( {\sigma }_{11}^{\left[ i \right] }\delta {{\varepsilon }_{11}}+{{\sigma }_{22}^{\left[ i \right] }}\delta {{\varepsilon }_{22}}+ 2{\sigma }_{12}^{\left[ i \right] }\delta {{\varepsilon }_{12}}+ 2{\sigma }_{13}^{\left[ i \right] }\delta {{\varepsilon }_{13}}+ 2{\sigma }_{23}^{\left[ i \right] }\delta {{\varepsilon }_{23}} \right ){{\,\mathrm{d\!}\,}}{{\mathscr {V} }^{\left[ i \right] }} \qquad \qquad \forall i\in \big \{1,2,3\big \}, \end{aligned}$$

(9)

$$\begin{aligned} \delta V&=-\mathop {\int }_{\mathscr {A}}^{{}}q~\delta w{{\,\mathrm{d\!}\,}}\mathscr {A}, \end{aligned}$$

(10)

where ${{\mathscr {V} }^{\left[ i \right] }}$ is the volume occupying by the i-th layer, and q is the total transverse load.

Five coupled governing equations can be derived in terms of displacement field by incorporating Eqs. (2)–(7a) and Eqs. (9)–(10) into Eq. (8) as follows

$$\begin{aligned} {\mathscr {L}_1}u \ +\ {\mathscr {L}_2}v \ +\ {\mathscr {L}_3}w \ +\ {\mathscr {L}_4}\zeta \ +\ {\mathscr {L}_5}\psi&= 0, \end{aligned}$$

(11a)

$$\begin{aligned} {\mathscr {L}_2}u \ +\ {\mathscr {L}_6}v \ +\ {\mathscr {L}_7}w \ +\ {\mathscr {L}_8}\zeta \ +\ {\mathscr {L}_9}\psi&= 0, \end{aligned}$$

(11b)

$$\begin{aligned} {\mathscr {L}_3}u \ +\ {\mathscr {L}_7}v \ +\ {\mathscr {L}_{10}}w \ +\ {\mathscr {L}_{11}}\zeta \ +\ {\mathscr {L}_{12}}\psi&= 0, \end{aligned}$$

(11c)

$$\begin{aligned} {\mathscr {L}_4}u \ +\ {\mathscr {L}_8}v \ +\ {\mathscr {L}_{11}}w \ +\ {\mathscr {L}_{13}}\zeta \ +\ {\mathscr {L}_{14}}\psi&= 0, \end{aligned}$$

(11d)

$$\begin{aligned} {\mathscr {L}_5}u \ +\ {\mathscr {L}_9}v \ +\ {\mathscr {L}_{12}}w \ +\ {\mathscr {L}_{14}}\zeta \ +\ {\mathscr {L}_{15}}\psi&= 0, \end{aligned}$$

(11e)

where ${\mathscr {L}_i}$, $\forall i\in \big \{1,\ldots ,15\big \}$ denote various differential operators, see appendix A.

2.5 Navier solution

Navier solution (Timoshenko and Woinowsky-Krieger 1959) expresses the deflection of simply-supported rectangular plates in terms of double trigonometric infinite series which naturally satisfy the essential boundary conditions. Following this approach, all the displacement terms are expressed as double trigonometric infinite series:

$$\begin{aligned} u(x_1,x_2)&=\underset{n=1}{\overset{\infty }{\mathop \sum }}\,\underset{m=1}{\overset{\infty }{\mathop \sum }}\,{{u}_{m\text {,n}}}\cos \left( \frac{m\pi }{a}x_1 \right) \sin \left( \frac{n\pi }{b}x_2 \right) , \end{aligned}$$

(12a)

$$\begin{aligned} v(x_1,x_2)&=\underset{n=1}{\overset{\infty }{\mathop \sum }}\,\underset{m=1}{\overset{\infty }{\mathop \sum }}\,{{v}_{m\text {,n}}}\sin \left( \frac{m\pi }{a}x_1 \right) \cos \left( \frac{n\pi }{b}x_2 \right) , \end{aligned}$$

(12b)

$$\begin{aligned} w(x_1,x_2)&=\underset{n=1}{\overset{\infty }{\mathop \sum }}\,\underset{m=1}{\overset{\infty }{\mathop \sum }}\,{{w}_{m\text {,n}}}\sin \left( \frac{m\pi }{a}x_1 \right) \sin \left( \frac{n\pi }{b}x_2 \right) , \end{aligned}$$

(12c)

$$\begin{aligned} \zeta (x_1,x_2)&=\underset{n=1}{\overset{\infty }{\mathop \sum }}\,\underset{m=1}{\overset{\infty }{\mathop \sum }}\,{{\zeta }_{m\text {,n}}}\cos \left( \frac{m\pi }{a}x_1 \right) \sin \left( \frac{n\pi }{b}x_2 \right) , \end{aligned}$$

(12d)

$$\begin{aligned} \psi (x_1,x_2)&=\underset{n=1}{\overset{\infty }{\mathop \sum }}\,\underset{m=1}{\overset{\infty }{\mathop \sum }}\,~{{\psi }_{m\text {,n}}}\sin \left( \frac{m\pi }{a}x_1 \right) \cos \left( \frac{n\pi }{b}x_2 \right) , \end{aligned}$$

(12e)

where $u_{m,n}$, $v_{m,n}$, $w_{m,n}$, $\psi _{m,n}$ and $\xi _{m,n}$ are unknown coefficients which satisfy Eqs. (11a)–(11e). Additionally, the transverse load q(x, y) can be also expanded as follows

$$\begin{aligned} q\left( x_1\text {,}x_2 \right) =\underset{n=1}{\overset{\infty }{\mathop \sum }}\,\underset{m=1}{\overset{\infty }{\mathop \sum }}\,{{Q}_{m\text {,n}}}\sin \left( \frac{m\pi }{a}x_1 \right) \sin \left( \frac{n\pi }{b}x_2 \right) , \end{aligned}$$

(13)

where $Q_{m,n}$ can be calculated as follows

$$\begin{aligned} {{Q}_{m\text {,n}}}=\frac{4}{a~b}\int _{0}^{a}\int _{0}^{b}q\left( x_1\text {,}x_2 \right) \sin \left( \frac{m\pi }{a}x_1 \right) \sin \left( \frac{n\pi }{b}x_2 \right) {{\,\mathrm{d\!}\,}}x_2\,{{\,\mathrm{d\!}\,}}x_1. \end{aligned}$$

(14)

Substituting Eqs. (12a)–(14) into Eqs. (11a)–(11e) leads to a system of algebraic equations in terms of the introduced unknown coefficients. These coupled algebraic equations are given in the appendix A.

Finally, the following dimensionless parameters are defined for quantifying the numerical results:

$$\begin{aligned} \overline{w}&\mathrel {:=}w_{c}\left( \frac{E h^{3}}{b^{4}q}\right) , \end{aligned}$$

(15a)

$$\begin{aligned} {\overline{\sigma }}_{11}&\mathrel {:=}\sigma _{11}\left( \frac{h^{2}}{b^{2} q}\right) , \end{aligned}$$

(15b)

$$\begin{aligned} {\overline{\sigma }}_{22}&\mathrel {:=}\sigma _{22}\left( \frac{h^{2}}{b^{2} q}\right) , \end{aligned}$$

(15c)

$$\begin{aligned} {\overline{\sigma }}_{12}&\mathrel {:=}\sigma _{12}\left( \frac{h^{2}}{b^{2} q}\right) , \end{aligned}$$

(15d)

$$\begin{aligned} {\overline{\sigma }}_{13}&\mathrel {:=}\sigma _{13}\left( \frac{h}{b q}\right) , \end{aligned}$$

(15e)

$$\begin{aligned} {\overline{\sigma }}_{23}&\mathrel {:=}\sigma _{23}\left( \frac{h}{b q}\right) , \end{aligned}$$

(15f)

$$\begin{aligned} h_{r}&\mathrel {:=}\frac{h_{c}}{h_{f}}, \end{aligned}$$

(15g)

$$\begin{aligned} \alpha&\mathrel {:=}\frac{a}{h}, \end{aligned}$$

(15h)

where $w_{c}$ is deflection at the plate centre, $h_{r}$ is the core-to-face thickness ratio, and $\alpha$ is the width-to-thickness ratio of the plate (reciprocal of thickness ratio).

3 Result and discussion

In this section, the developed analytical models are benchmarked against a full-field finite element model. Then, a parametric study is conducted to further understand the behaviour of the model.

3.1 Validation of the model

Due to the limited experimental results available in the literature, the developed models are validated against the results of

• 1. The analytical model of Reddy (2003) where a three-layer (0/90/0) square laminate plate is subjected to sinusoidal loading; and

• 2. A full-field finite element model (Javanbakht and Öchsner 2017, 2018) created by the ABAQUS commercial package.

Finite element model. A full-field finite element model was created accounting for all the mesoscopic details. Eight-node isoparametric quadrilateral linear elements were used to discretise the geometry of both core and face sheets. A sinusoidal distributed load with an amplitude of 100 N, and wavelengths of 2a and 2b (along x and y directions, respectively) was applied to the top face. The Young’s modulus, Poisson’s ratio, and mass density of the sample were assumed to be 69 GPa, 0.3, and 2700 ${\textrm{Kg}}/{\textrm{m}^{3}}$, respectively. The side faces of the model were fixed along three directions, see Fig. 2a.

Mesh convergence study To achieve mesh independence, the total reaction force ($F_\textrm{tot}$) and maximum deflection ($w_\textrm{c}$) were plotted against various mesh densities (Javanbakht et al. 2017):

$$\begin{aligned} \gamma \mathrel {:=}\frac{1}{\ell }, \end{aligned}$$

(16)

where $\ell$ is the characteristic length of the mesh. A mesh density of $0.125\,{1}/{\textrm{mm}}$ was used based on the mesh sensitivity analysis in Fig. 2b where the maximum deflection and total reaction force were used as target values.

Fig. 2

Finite element model: a fixed boundary conditions of the circumference (in orange) and surface loading of the top skin (in pink), b mesh sensitivity analysis

Benchmarking against the finite element model. Under a linear static analysis, the dimensionless maximum deflection ($\overline{w}$) was calculated at the centre of the sandwich panel, see Table 2. Overall, the percentage relative error of models are below 14% among which the fifth-order theory provides the best estimate for deflection.

Table 2 Maximum deflection of the honeycomb sandwich panel against the finite element results

Analytical benchmark model. In Table 3, the maximum deflection of the plate and normal/shear stress components at various monitoring points are calculated using the developed models; The results are compared against TSDT, MPT and 3D elasticity solution (ELS) of Reddy (2003). The transverse shear stress at the middle of the core ${\overline{\sigma }}_{23}({a}/{2},0,0)$) is the least accurate results,compared to ELS, as relative percentage errors up to 16% are observed. In contrast, maximum deflection at the centre of the panel along with the other stress values are in good agreement with the benchmark model.

Table 3 Validation of the maximum deflection and stress components for a three-layer (0/90/0) square laminate plate modelled in Reddy (2003)

3.2 Parametric analysis of the core mechanical properties

To better comprehend the behaviour of the developed analytical models, a parametric analysis was conducted for the isolated regular and re-entrant honeycomb cores, i.e., negative and positive inclination angles, respectively. To provide dimensionless results, the effective elastic moduli were normalised relative those of the face sheets $\left(E\equiv E^{[1]}\equiv E^{[3]}=69\,\textrm{GPa}\right)$, i.e., the normalised elastic moduli along the principal directions $\left( {E^{[2]}_1}/{E} \,\text{and}\, {E^{[2]}_2}/{E}\right)$ and normalised core transverse shear modulus $\left( G_{23}^{\left[ 2 \right] }/G\right)$ were used in presenting the results. The sensitivity of various material properties to geometrical variation is presented in this subsection, see Fig. 3. Note that all the results are presented for a constant thickness-to-length ratio of $\eta _3=0.1$; increasing this ratio only magnifies the values, see the numerators in Eq. (7a).

Fig. 3

Variation of the core properties due to its geometrical variation: a core Poisson’s ratio versus cell wall angle, b core anisotropy ratio versus cell wall angle, c core Poisson’s ratio versus normalised elastic moduli of core, and d core Poisson’s ratio versus normalised shear modulus

Core auxeticity. Cell wall angle triggers the auxetic behaviour of honeycomb cells, see Fig. 3a. Positive cell wall angles ($\theta >0^\circ$) induce negative Poisson’s ratio whereas the negative angles represent the regular honeycomb structures in the current formulation. In the vicinity of $\theta =0^\circ$, a sharp transition between auxetic and regular behaviour occurs, which is a result of changing the internal geometry of the core layer from inverted honeycomb to the regular hexagonal arrangement. Note that at larger angles a zero Poisson’s ratio is asymptotically obtained, irrespective of the auxetic or regular behaviour. Finally, in larger cell aspect ratios ($\eta _1$), the jump between two behaviours become milder but vanishes asymptotically faster.

Core anisotropy. The geometry of the cell adjusts the anisotropy of the core, see Fig. 3b. By taking the elastic moduli ratios of two principal directions $\left({E^{[2]}_1}/{E^{[2]}_2}\right)$ as an anisotropy metric, it can be seen that higher cell wall angles increase anisotropy. For negative cell wall angles, a sharper rise denotes the increased sensitivity of anisotropy in the regular hexagonal arrangement. Namely, more extreme anisotropy can be achieved in regular honeycomb cores compared to the auxetic one. More importantly, negligible cell wall angles (about $-10^\circ<\theta <+10^\circ$) induce the least amount of anisotropic response in the core—this range is about the same for both auxetic and regular cores. Note that at zero degrees, the formulation represents a rectangular box cross-section, which can be completely isotropic if it becomes a square box. Therefore, the mentioned range of angles becomes more limited for higher cell aspect ratios where anisotropy is more pronounced.

Elastic moduli and Poisson’s ratio. The relative elastic moduli along two principal directions $\left(E _{1}^{\left[ 2 \right] }/E\, \text{and}\,E _{2}^{\left[ 2 \right] }/E\right)$ were plotted for three values of cell aspect ratio ($\eta _{1}$=1.8, 2.4 and 3) in Fig. 3c. In both re-entrant and regular cases, the following observations are obtained—provided that the absolute value of Poisson’s ratio is used for the auxetic case. Decreasing the value of Poisson’s ratio increases the elastic modulus along 1-axis in both regular and auxetic cores. In either case, elastic modulus along 2-axis may increase or decrease depending on other principal value of elastic modulus. Zero Poisson’s ratio corresponds to increased elastic modulus along 1-axis whereas along 2-axis, either a more restricted increase occurs or its value vanishes. The elastic modulus value along 2-axis is more sensitive to the cell aspect ratio, i.e., higher aspect ratios results in smaller Poisson’s ratio and a smaller maximum value for the same range of Poisson’s ratios. On the other hand, $E_1$ seems to be less sensitive to the aspect ratio change as $l_2$ was kept constant during this variation.

Transverse shear modulus and Poisson’s ratio. Fig. 3d illustrates the variation of Poisson’s ratio versus the shear modulus ratio. Similar to normalised elastic moduli, higher aspect ratios produce more controlled stiffness values in the same range of Poisson’s ratios. For the regular core, normalised shear modulus decreases by increasing the cell wall angle; this reduction is more severe for larger aspect ratios. In contrast, the auxetic core experiences a slight increase before starting the decreasing regime; similarly, this increase is more severe for smaller aspect ratios. It is noted that smaller aspect ratios can potentially provide larger transverse shear moduli for a specific Poisson’s ratio.

3.3 Mechanical response of the sandwich panel

In this subsection, a parametric study is conducted to reveal the behaviour of the sandwich panel with an auxetic core under linear static loading. Various plate theories are used to calculate the deflection under sinusoidal distributed load (amplitude of q, and wavelengths 2a and 2b in the $x_1$ and $x_2$ directions, respectively) and the transverse shear stress of the panel, see Fig. 4. In these structures, isotropic face sheet are assumed to have an elastic modulus of ($E\equiv E^{[1]}\equiv E^{[3]}=69\,\textrm{GPa}$ and a shear modulus of $\left(G\equiv G^{[1]}\equiv G^{[3]}=26.5\,\textrm{GPa}\right)$. The core-to-face-sheet thickness ratio is assumed to be ${h_\textrm{c}}/{h_\textrm{f}}=4$ for a total thickness of $h=0.1$.

Maximum deflection dependence on the cell geometry. As illustrated in Fig. 4a, all plate theories asymptotically result in the same deflection at higher values of $\alpha$ (reciprocal of thickness ratio), i.e., for thin sandwich panels, all theories correspond to CPT. In contrast at lower values of $\alpha$, higher-order theories deviate from the solution of CPT while MPT stand-outs with an underestimation of the values. This could be attributed to dropping the shear contribution of deflection in MPT ($g=0$). The most compliant response is that of FSDT whereas TSDT and HSDT identically show the stiffest behaviour (excluding MPT). Finally, the insensitivity of CPT to thickness changes is clearly depicted. It is understood that in terms of deflection values, the shear contribution of deflection-dependent component (g) is more detrimental compared to the independent rotations (via f). In addition, the deflections can become up to 2.5 times of the shear-rigid theories for thick sandwich panels.

Transverse shear stress dependence on the cell geometry. Transverse shear distribution of the panel is depicted in Fig. 4b. From top to bottom, the jumps in the shear stress values mark the regions for top face sheet, core, and bottom face sheet. In all layers, CPT cannot capture any shear stress distribution. MPT fails at satisfying the traction-free boundary conditions in the face sheet layers while estimating a small shear value through the core. The advantage of higher-order theories is highlighted by providing much better estimates in all layers and satisfying the traction-free conditions. Most higher-order theories seem to be in agreement with each other except at the middle of the core and in the skin layer around the skin-core interface. In the skin layers and in the core layer at the vicinity of the skin-core interface, stress estimates follow the same trend, i.e., HSDT and FSDT give the highest and lowest stress values, respectively. In contrast, this trend reverses about the middle of the core. Similar to maximum deflection, the estimations of TSDT and HSDT are very similar denoting the lowest stress on the mid-plane (except the CLT and MPT); on the other hand, the highest stress on the mid-plane is generated by FSDT. Most unreliable results are provided CPT and MPT—especially in the core layer.

Fig. 4

Estimations of various plate theories for the sandwich panel: a maximum dimensionless deflection, and b dimensionless transverse shear stress of the panel at mid-edge (a/2, 0)

Effect of core material properties. In Fig. 5, FSDT was used to illustrate the variation of the maximum deflections ($\overline{w}$) of both regular and re-entrant honeycomb structures against the variation of their core material properties—which is a direct cause of varying cell wall angle ($-70^\circ \le \theta \le +70^\circ$), see Figs. 3a and 3b. Namely, the anisotropy of the core $\left({E^{[2]}_1}/{E^{[2]}_2}\right)$ and core Poisson’s ratio can be adjusted by fine-tuning the cell wall angle. In consequence, the maximum deflection of the sandwich panel can be controlled, too. In either auxetic or regular behaviour, increasing the wall thickness-to-length ratio ($\eta _3$) reduces the deflection since stiffness of the structure increases. On the contrary, increasing the core anisotropy causes a reduction in deflection for auxetic behaviour while slightly increases the deflection in the regular one, see Fig. 5b. In the auxetic core, increasing the positive cell wall angle results in higher anisotropy, and sudden drop in the negative Poisson’s ratio which is followed by an asymptotic increase towards zero. Consequently, the deflection of the plate decreases for the auxetic core when the negative Poisson’s ratio is nullified. It should be noted that deflection experiences more sensitivity to the values of Poisson’s ratio in smaller cell aspect ratios, see Fig. 5a. On the other hand, deflection seems to be less sensitive to the changes of the positive values of Poisson’s ratio except producing a slight increase. In summary to control deflection, it is suggested to use the auxetic core and increase the cell wall angle.

Fig. 5

Effect of core material properties on maximum deflection of the honeycomb core based on the results of FSDT: a variation of core Poisson’s ratio for different thickness-to-length ratios ($\eta _{3}$), and b variation of core elastic modulus ratio for different cell aspect ratios ($\eta _{1}$)

Effect of the core-to-face thickness ratio. Fig. 6 shows the influence of auxetic core-to-skin thickness ratio ($h_{r}$) on the maximum dimensionless deflection of the plate. Increasing the $h_{r}$ ratio magnifies the maximum deflection because thicker auxetic cores are softer. The aspect ratio and the thickness-to-length ratios of the cell have negligible effect for $h_{r}<2$; in contrast, at higher values of $h_{r}$, the difference is more noticeable. This can be attributed to the emerging dominance of core properties as its thickness increases.

Fig. 6

Variation of maximum deflection of the sandwich panel versus the core-to-skin thickness ratio ($h_\textrm{r}$) for different values of a cell aspect ratio ($\eta _1$), and b auxetic thickness-to-length ratio ($\eta _3$)

Transverse shear stress dependence on the cell geometry. The variation of dimensionless transverse shear stress versus various geometrical parameters of an auxetic core ($\theta =30^\circ$) is depicted in Fig. 7. Increasing the cell aspect ratio reduces the transverse shear stress in the core; this effect is more pronounced in the middle of the core and slightly reduces towards the skins, see Fig. 7a. In contrast, higher cell aspect ratios has the opposite effect in the skins and increases the transverse shear stress therein. Nevertheless, towards the outer boundaries of the skins, the stress distribution diminishes to comply with the traction-free boundary conditions. Increasing the thickness-to-length ratio has the effect opposite to the cell aspect ratio, see Fig. 7b. Namely, higher thickness-to-length ratios increase the transverse shear in the core while reducing it in the skins. However, the increase of transverse shear stress becomes less sensitive to the thickness-to-length ratio towards the skins.

Increasing the cell wall angle decreases the transverse shear stress both in the auxetic core and in the skins, see Fig. 7d; this effect is slightly more pronounced in the middle of the core. Nevertheless, the shear modulus can increase or decrease as a function of cell wall angle, see Fig. 3d. For instance, take $\eta _{1}=1.8$ and $\eta _{3}=0.1$, shear modulus peaks at about $\theta$=30°after which the stiffness starts to decline and asymptotically approach zero. Thus, comparing angles more than 40°, the stiffness is diminished and the shear stress will increase. Therefore, increasing cell wall angle can have an opposite effect depending on its value; this highlights the importance of selecting a correct cell wall angle for minimising shear stress.

Fig. 7

Through-thickness distribution of dimensionless transverse shear stress versus a cell aspect ratio, b thickness-to-length ratio, c cell wall angle (contour), and d) cell wall angle (graph) for a re-entrant honeycomb under SDL

4 Conclusion

In the current study, Navier solution has been employed to investigate the static bending response of simply supported sandwich panel with regular and re-entrant honeycomb core. Various classic and higher order theories were employed under a unified scheme to formulate the behaviour of the structure under a sinusoidal loading. The analytical model was validated using a finite element model and some benchmark values available in the literature. Extensive parametric studies were carried out to shed light on the intricate behaviour of this particular structure. It was found that the behaviour of the core can be adjusted by fine-tuning the cell wall angle ($\theta$), the aspect ratio ($\eta _1$), the thickness-to-length ratio ($\eta _3$), and core-to-skin thickness ($h_\text {r}$). These parameters affect the auxetic/regular behaviour, the value of Poisson’s ratio, anisotropy of the cell, out-of-plane shear modulus, transverse shear stress distribution, and deflection of the panel. Particularly, the cell wall angle has an overarching effect on other parameters.

The following key findings can be highlighted about the mechanical response of the core:

• Cell wall angles ranging about $-10^\circ<\theta <+10^\circ$ results in the least anisotropic response of the auxetic and regular core.

• Increasing the cell wall angle can result in highly anisotropic behaviour of the auxetic core, i.e., the contrast of elastic moduli increases from below 0.2 to 20 at higher aspect ratios.

• In estimating the deflection using higher-order theories, the deflection-dependent component of the unified solution (g) in Eq. (2) is more critical than independent rotations (f). Considering the shear deformations results in maximum deflections 2.5 times those of the CPT predictions.

• The main advantage of higher-order theories is providing better estimates of transverse shear stress and deflection while satisfying the traction-free boundary conditions.

• Cell aspect ratio controls the sensitivity of the core response to geometrical variations. For instance, normalised shear modulus experiences higher variations in both auxetic and regular cores.

• For core-to-skin thickness ratios smaller than two ($h_{r}<2$), the cell aspect ratio and thickness-to-length ratio have negligible effect of the maximum deflection of the sandwich panel.

• By increasing the cell wall angle within a certain range can reduce the transverse shear stress in both auxetic core and skin layers, e.g., within $0^\circ<\theta <+\,40^\circ$ in the current study.

By combining the generalised Gibson’s formulation with a family of higher-order plate theories, this study provides an analytical estimation of the linear static response of a sandwich panel. The approach can be used for any unit cells that can be modelled by a beam theories. In addition to static response, it can be used in dynamic and vibration analyses. More importantly, it was shown that no one-to-one relationship exists between auxeticity, anisotropy, and shear rigidity in re-entrant honeycomb auxetics; thus, geometrical parameters must be selected carefully during design to fine-tune the desired mechanical response. Future studies might include the viscoelastic behaviour of such structures.

Appendix

Dependency of various functions are summarised as follows:

$$\begin{aligned} u&\equiv u(x_1,x_2), \end{aligned}$$

(A.1a)

$$\begin{aligned} v&\equiv v(x_1,x_2), \end{aligned}$$

(A.1b)

$$\begin{aligned} w&\equiv w(x_1,x_2), \end{aligned}$$

(A.1c)

$$\begin{aligned} \psi&\equiv \psi (x_1,x_2), \end{aligned}$$

(A.1d)

$$\begin{aligned} \zeta&\equiv \zeta (x_1,x_2). \end{aligned}$$

(A.1e)

The expanded form of Eqs. (11a)–(11e) can be written as follows:

$$\begin{aligned}&A_1 v_{,12} + A_2 \psi _{,12} + A_3 w_{,122} \nonumber \\&\quad + B_1 u_{,11} +B_2\zeta _{,11} + B_3 w_{,111} \nonumber \\&\quad + C_1\left( v_{,12}+C_2 \psi _{,12} +u_{,22}\right) \nonumber \\&\quad +C_2 \zeta _{,22}+2C_3 w_{,122} =0, \end{aligned}$$

(A.2a)

$$\begin{aligned}&A_1 u_{,12}+A_3 w_{,112}+A_2 \zeta _{,12}\nonumber \\&\quad +C_1 u_{,12}+2C_3 w_{,112}+C_2 \zeta _{,12}\nonumber \\&\quad +E_1 v_{,22}+E_3 w_{,222}+E_2 \psi _{,22}\nonumber \\&\quad +C_1 v_{,11}+C_2 \psi _{,11}=0, \end{aligned}$$

(A.2b)

$$\begin{aligned}&-A_3 u_{,122}-A_3 v_{,112}-2A_5 w_{,1122}-A_4 \psi _{,112}\nonumber \\&\quad -A_4\zeta _{,122}-2C_3 u_{,122}-2C_3 v_{,112}-4C_5 w_{,1122}\nonumber \\&\quad -2C_4 \psi _{,112}-2C_4\zeta _{,122}-B_3 u_{,111}-B_5w_{,1111}-B_4 \zeta _{,111}\nonumber \\&\quad -E_3 v_{,222}-E_5 w_{,2222}-E_4\psi _{,222}+E_1 K_s w_{,22}\nonumber \\&\quad +2D_2 K_s w_{,22}+D_5 K_s w_{,22}+D_3 K_s \psi _{,2}+D_4 K_s\psi _{,2}\nonumber \\&\quad +G_1 K_s w_{,11}+2G_2 K_s w_{,11}+G_5 K_s w_{,11}\nonumber \\&\quad +G_3 K_s\zeta _{,1}+G_4 K_s \zeta _{,1}+q=0, \end{aligned}$$

(A.2c)

$$\begin{aligned}&A_2 v_{,12}+A_4 w_{,122}+A_6 \psi _{,12}+C_2 v_{,12}+2C_4 w_{,122}\nonumber \\&\quad +C_6 \psi _{,12}+B_2 u_{,11}+B_4 w_{,111} +B_6 \zeta _{,11}\nonumber \\&\quad +C_2u_{,22}+C_6 \zeta _{,22}-G_3 K_s w_{,1}\nonumber \\&\quad -G_4 K_s w_{,1}-G_6 K_s \zeta =0, \end{aligned}$$

(A.2d)

$$\begin{aligned}&A_2 u_{,12}+A_4 w_{,112}+A_6 \zeta _{,12}+C_2 u_{,12}+2C_4 w_{,112}+C_6 \zeta _{,12}\nonumber \\&\quad +E_2 v_{,22}+E_4 w_{,222}+E_6 \psi _{,22}+C_2v_{,11}\nonumber \\&\quad +C_6 \psi _{,11}-D_3 K_s w_{,2}-D_4 K_s w_{,2}-D_6 K_s \psi =0. \end{aligned}$$

(A.2e)

The shear correction factor $K_{s}$ is 5/6 for FSDT and 1 for other theories given in Table 1. Material coefficients of Eqs. (A.2a)–(A.2e) are given as follows:

$$\begin{aligned}&{{ \begin{bmatrix} {{A}_{1}} &{} {{A}_{2}} &{} {{A}_{3}} &{} {{A}_{4}} &{} {{A}_{5}} &{} {{A}_{6}} \\ {{B}_{1}} &{} {{B}_{2}} &{} {{B}_{3}} &{} {{B}_{4}} &{} {{B}_{5}} &{} {{B}_{6}} \\ {{C}_{1}} &{} {{C}_{2}} &{} {{C}_{3}} &{} {{C}_{4}} &{} {{C}_{5}} &{} {{C}_{6}} \\ {{E}_{1}} &{} {{E}_{2}} &{} {{E}_{3}} &{} {{E}_{4}} &{} {{E}_{5}} &{} {{E}_{6}} \\ \end{bmatrix} }} =\underset{i=1}{\overset{3}{\mathop \sum }}\,\mathop {\int }_{{{h}_{i}}}^{{{h}_{i-1}}} \left\{ Q_{12}^{\left[ i \right] },~Q_{11}^{\left[ i \right] },~Q_{66}^{\left[ i \right] },~Q_{22}^{\left[ i \right] } \right\} ^{T}\nonumber \\&\left\{ 1,~f,~g,~fg,~g^{2},~f^{2} \right\} {{\,\mathrm{d\!}\,}}x_3 \end{aligned}$$

(A.3a)

$$\begin{aligned}&{{ \begin{bmatrix} {{D}_{1}} &{} {{D}_{2}} &{} {{D}_{3}} &{} {{D}_{4}} &{} {{D}_{5}} &{} {{D}_{6}} \\ {{G}_{1}} &{} {{G}_{2}} &{} {{G}_{3}} &{} {{G}_{4}} &{} {{G}_{5}} &{} {{G}_{6}} \\ \end{bmatrix} }} =\underset{i=1}{\overset{3}{\mathop \sum }}\,\mathop {\int }_{{{h}_{i}}}^{{{h}_{i-1}}} \left\{ Q_{44}^{\left[ i \right] },~Q_{55}^{\left[ i \right] } \right\} ^{T}\nonumber \\&\left\{ 1,~g_{,3},~f_{,3},~f_{,3}g_{,3},~g_{,3}^{2},~f_{,3}^{2} \right\} {{\,\mathrm{d\!}\,}}x_3. \end{aligned}$$

(A.3b)

Linear algebraic system of equations obtained by inserting trial functions into governing equations are given as follows:

$$\begin{aligned}&-\frac{{\pi }^{3}}{{B}_{3}}{{m}^{3}}{{w}_{m,n}}{{{a}^{3}}}-\frac{{{\pi }^{2}}{{B}_{2}}{{m}^{2}}{{\zeta }_{m,n}}}{{{a}^{2}}}-\frac{{{\pi }^{2}}{{B}_{1}}{{m}^{2}}{{u}_{m,n}}}{{{a}^{2}}}\nonumber \\&-\frac{{{\pi }^{3}}{{A}_{3}}m{{n}^{2}}{{w}_{m,n}}}{a{{b}^{2}}}-\frac{{{\pi }^{2}}{{A}_{1}}mn{{v}_{m,n}}}{ab}-\frac{{{\pi }^{2}}{{A}_{2}}mn{{\psi }_{m,n}}}{ab} \nonumber \\&\quad -\frac{2{{\pi }^{3}}{{C}_{3}}m{{n}^{2}}{{w}_{m,n}}}{a{{b}^{2}}}-\frac{{{\pi }^{2}}{{C}_{1}}mn{{v}_{m,n}}}{ab}-\frac{{{\pi }^{2}}{{C}_{2}}mn{{\psi }_{m,n}}}{ab}\nonumber \\&-\frac{{{\pi }^{2}}{{C}_{2}}{{n}^{2}}{{\zeta }_{m,n}}}{{{b}^{2}}}-\frac{{{\pi }^{2}}{{C}_{1}}{{n}^{2}}{{u}_{m,n}}}{{{b}^{2}}}=0, \end{aligned}$$

(A.4a)

$$\begin{aligned}&-\frac{{{\pi }^{3}}{{A}_{3}}{{m}^{2}}n{{w}_{m,n}}}{{{a}^{2}}b} -\frac{2{{\pi }^{3}}{{C}_{3}}{{m}^{2}}n{{w}_{m,n}}}{{{a}^{2}}b} -\frac{{{\pi }^{2}}{{C}_{1}}{{m}^{2}}{{v}_{m,n}}}{{{a}^{2}}}\nonumber \\&-\frac{{{\pi }^{2}}{{C}_{2}}{{m}^{2}}{{\psi }_{m,n}}}{{{a}^{2}}} -\frac{{{\pi }^{2}}{{A}_{2}}mn{{\zeta }_{m,n}}}{ab}-\frac{{{\pi }^{2}}{{A}_{1}}mn{{u}_{m,n}}}{ab} \nonumber \\&\quad -\frac{{{\pi }^{2}}{{C}_{2}}mn{{\zeta }_{m,n}}}{ab}-\frac{{{\pi }^{2}}{{C}_{1}}mn{{u}_{m,n}}}{ab}-\frac{{{\pi }^{3}}{{\text {B}}_{3}}{{n}^{3}}{{w}_{m,n}}}{{{b}^{3}}}\nonumber \\&-\frac{{{\pi }^{2}}{{\text {B}}_{1}}{{n}^{2}}{{v}_{m,n}}}{{{b}^{2}}} -\frac{{{\pi }^{2}}{{\text {B}}_{2}}{{n}^{2}}{{\psi }_{m,n}}}{{{b}^{2}}}=0, \end{aligned}$$

(A.4b)

$$\begin{aligned}&-\frac{{{\pi }^{4}}{{B}_{5}}{{m}^{4}}{{w}_{m,n}}}{{{a}^{4}}}-\frac{{{\pi }^{3}}{{B}_{4}}{{m}^{3}}{{\zeta }_{m,n}}}{{{a}^{3}}}-\frac{{{\pi }^{3}}{{B}_{3}}{{m}^{3}}{{u}_{m,n}}}{{{a}^{3}}}\nonumber \\&-\frac{2{{\pi }^{4}}{{A}_{5}}{{m}^{2}}{{n}^{2}}{{w}_{m,n}}}{{{a}^{2}}{{b}^{2}}}-\frac{{{\pi }^{3}}{{A}_{3}}{{m}^{2}}n{{v}_{m,n}}}{{{a}^{2}}b}-\frac{{{\pi }^{3}}{{A}_{4}}{{m}^{2}}n{{\psi }_{m,n}}}{{{a}^{2}}b} \nonumber \\&\quad -\frac{4{{\pi }^{4}}{{C}_{5}}{{m}^{2}}{{n}^{2}}{{w}_{m,n}}}{{{a}^{2}}{{b}^{2}}}-\frac{2{{\pi }^{3}}{{C}_{3}}{{m}^{2}}n{{v}_{m,n}}}{{{a}^{2}}b}-\frac{2{{\pi }^{3}}{{C}_{4}}{{m}^{2}}n{{\psi }_{m,n}}}{{{a}^{2}}b}\nonumber \\&-\frac{{{\pi }^{2}}{{G}_{1}}{{K}_{s}}{{m}^{2}}{{w}_{m,n}}}{{{a}^{2}}}-\frac{2{{\pi }^{2}}{{G}_{2}}{{K}_{s}}{{m}^{2}}{{w}_{m,n}}}{{{a}^{2}}}\nonumber \\&\quad -\frac{{{\pi }^{2}}{{G}_{5}}{{K}_{s}}{{m}^{2}}{{w}_{m,n}}}{{{a}^{2}}}-\frac{{{\pi }^{3}}{{A}_{4}}m{{n}^{2}}{{\zeta }_{m,n}}}{a{{b}^{2}}}-\frac{{{\pi }^{3}}{{A}_{3}}m{{n}^{2}}{{u}_{m,n}}}{a{{b}^{2}}}\nonumber \\&-\frac{2{{\pi }^{3}}{{C}_{4}}m{{n}^{2}}{{\zeta }_{m,n}}}{a{{b}^{2}}}-\frac{2{{\pi }^{3}}{{C}_{3}}m{{n}^{2}}{{u}_{m,n}}}{a{{b}^{2}}}-\frac{\pi {{G}_{3}}{{K}_{s}}m{{\zeta }_{m,n}}}{a}\nonumber \\&\quad -\frac{\pi {{G}_{4}}{{K}_{s}}m{{\zeta }_{m,n}}}{a}-\frac{{{\pi }^{4}}{{\text {B}}_{5}}{{n}^{4}}{{w}_{m,n}}}{{{b}^{4}}}-\frac{{{\pi }^{3}}{{\text {B}}_{3}}{{n}^{3}}{{v}_{m,n}}}{{{b}^{3}}}\nonumber \\&\quad -\frac{{{\pi }^{3}}{{\text {B}}_{4}}{{n}^{3}}{{\psi }_{m,n}}}{{{b}^{3}}} -\frac{{{\pi }^{2}}{{\text {D}}_{1}}{{K}_{s}}{{n}^{2}}{{w}_{m,n}}}{{{b}^{2}}} -\frac{2{{\pi }^{2}}{{\text {D}}_{2}}{{K}_{s}}{{n}^{2}}{{w}_{m,n}}}{{{b}^{2}}}\nonumber \\&\quad -\frac{{{\pi }^{2}}{{\text {D}}_{5}}{{K}_{s}}{{n}^{2}}{{w}_{m,n}}}{{{b}^{2}}} -\frac{\pi {{\text {D}}_{3}}{{K}_{s}}n{{\psi }_{m,n}}}{b}-\frac{\pi {{\text {D}}_{4}}{{K}_{s}}n{{\psi }_{m,n}}}{b}+{{Q}_{m,n}}=0, \end{aligned}$$

(A.4c)

$$\begin{aligned}&-\frac{{{\pi }^{3}}{{B}_{4}}{{m}^{3}}{{w}_{m,n}}}{{{a}^{3}}}-\frac{{{\pi }^{2}}{{B}_{6}}{{m}^{2}}{{\zeta }_{m,n}}}{{{a}^{2}}}-\frac{{{\pi }^{2}}{{B}_{2}}{{m}^{2}}{{u}_{m,n}}}{{{a}^{2}}}\nonumber \\&-\frac{{{\pi }^{3}}{{A}_{4}}m{{n}^{2}}{{w}_{m,n}}}{a{{b}^{2}}}-\frac{{{\pi }^{2}}{{A}_{2}}mn{{v}_{m,n}}}{ab}-\frac{{{\pi }^{2}}{{A}_{6}}mn{{\psi }_{m,n}}}{ab} \nonumber \\&\quad -\frac{2{{\pi }^{3}}{{C}_{4}}m{{n}^{2}}{{w}_{m,n}}}{a{{b}^{2}}}-\frac{{{\pi }^{2}}{{C}_{2}}mn{{v}_{m,n}}}{ab}-\frac{{{\pi }^{2}}{{C}_{6}}mn{{\psi }_{m,n}}}{ab}\nonumber \\&-\frac{\pi {{G}_{3}}{{K}_{s}}m{{w}_{m,n}}}{a} -\frac{\pi {{G}_{4}}{{K}_{s}}m{{w}_{m,n}}}{a}-\frac{{{\pi }^{2}}{{C}_{6}}{{n}^{2}}{{\zeta }_{m,n}}}{{{b}^{2}}}\nonumber \\&\quad -\frac{{{\pi }^{2}}{{C}_{2}}{{n}^{2}}{{u}_{m,n}}}{{{b}^{2}}} -{{G}_{6}}{{K}_{s}}{{\zeta }_{m,n}}=0, \end{aligned}$$

(A.4d)

$$\begin{aligned}&-\frac{{{\pi }^{3}}{{A}_{4}}{{m}^{2}}n{{w}_{m,n}}}{{{a}^{2}}b}-\frac{2{{\pi }^{3}}{{C}_{4}}{{m}^{2}}n{{w}_{m,n}}}{{{a}^{2}}b}-\frac{{{\pi }^{2}}{{C}_{2}}{{m}^{2}}{{v}_{m,n}}}{{{a}^{2}}}\nonumber \\&-\frac{{{\pi }^{2}}{{C}_{6}}{{m}^{2}}{{\psi }_{m,n}}}{{{a}^{2}}}-\frac{{{\pi }^{2}}{{A}_{6}}mn{{\zeta }_{m,n}}}{ab}-\frac{{{\pi }^{2}}{{A}_{2}}mn{{u}_{m,n}}}{ab} \nonumber \\&\quad -\frac{{{\pi }^{2}}{{C}_{6}}mn{{\zeta }_{m,n}}}{ab}-\frac{{{\pi }^{2}}{{C}_{2}}mn{{u}_{m,n}}}{ab}-\frac{{{\pi }^{3}}{{\text {B}}_{4}}{{n}^{3}}{{w}_{m,n}}}{{{b}^{3}}}\nonumber \\&-\frac{{{\pi }^{2}}{{\text {B}}_{2}}{{n}^{2}}{{v}_{m,n}}}{{{b}^{2}}}-\frac{{{\pi }^{2}}{{\text {B}}_{6}}{{n}^{2}}{{\psi }_{m,n}}}{{{b}^{2}}}-\frac{\pi {{\text {D}}_{3}}{{K}_{s}}n{{w}_{m,n}}}{b}\nonumber \\&\quad -\frac{\pi {{\text {D}}_{4}}{{K}_{s}}n{{w}_{m,n}}}{b}-{{\text {D}}_{6}}{{K}_{s}}{{\psi }_{m,n}}=0, \end{aligned}$$

(A.4e)