Abstract
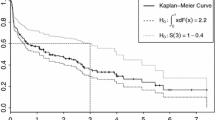
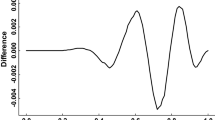
We review limit theory and inequalities for the Kaplan–Meier Kaplan and Meier (J Am Stat Assoc 53:457–481, 1958) product limit estimator of a survival function on the whole line \({{\mathbb{R}}}\) . Along the way we provide bounds for the constant in an interesting inequality due to Biotouzé et al. (Ann Inst H Poincaré Probab Stat 35:735–763, 1999), and provide some numerical evidence in support of one of their conjectures.
Similar content being viewed by others
References
Birman MŠ, Solomjak MZ (1967) Piecewise polynomial approximations of functions of classes \(W{_p}^{\alpha}\) . Mat Sb (NS) 73(115):331–355
Bitouzé D, Laurent B and Massart P (1999). A Dvoretzky-Kiefer-Wolfowitz type inequality for the Kaplan- Meier estimator. Ann Inst H Poincar Probabé Stat 35: 735–763
Breslow N and Crowley J (1974). A large sample study of the life table and product limit estimates under random censorship. Ann Stat 2: 437–453
Burke MD, Csörgő S and Horváth L (1981). Strong approximations of some biometric estimates under random censorship. Z Wahrsch Verw Gebiete 56: 87–112
Chen K and Ying Z (1996). A counterexample to a conjecture concerning the Hall-Wellner band. Ann Stat 24: 641–646
Csörgő S (1996). Universal Gaussian approximations under random censorship. Ann Stat 24: 2744–2778
Csörgő S and Horváth L (1983). The rate of strong uniform consistency for the product-limit estimator. Z Wahrsch Verw Gebiete 62: 411–426
Csörgő S and Horváth L (1986). Confidence bands from censored samples. Canad J Stat 14: 131–144
Dvoretzky A, Kiefer J and Wolfowitz J (1956). Asymptotic minimax character of the sample distribution function and of the classical multinomial estimator. Ann Math Stat 27: 642–669
Gill RD (1980) Censoring and stochastic integrals, vol. 124 of Mathematical Centre Tracts. Mathematisch Centrum, Amsterdam
Gill R (1983). Large sample behaviour of the product-limit estimator on the whole line. Ann Stat 11: 49–58
Gill RD (1994). Glivenko–Cantelli for Kaplan–Meier. Math Methods Stat 3: 76–87
Gillespie MJ and Fisher L (1979). Confidence bands for the Kaplan–Meier survival curve estimate. Ann Stat 7: 920–924
Giné E and Guillou A (1999). Laws of the iterated logarithm for censored data. Ann Probab 27: 2042–2067
Gu M (1991) The Chung–Smirnov law for the product-limit estimator under random censorship. Chin. Ann Math Ser B 12:96–105. A Chinese summary appears in Chin Ann Math Ser A 12(1):119
Gu MG and Lai TL (1990). Functional laws of the iterated logarithm for the product-limit estimator of a distribution function under random censorship or truncation. Ann Probab 18: 160–189
Hall WJ and Wellner JA (1980). Confidence bands for a survival curve from censored data. Biometrika 67: 133–143
Hollander M, McKeague IW and Yang J (1997). Likelihood ratio-based confidence bands for survival functions. J Am Stat Assoc 92: 215–226
Hollander M and Peña E (1989). Families of confidence bands for the survival function under the general random censorship model and the Koziol-Green model. Can J Stat 17: 59–74
Kaplan EL and Meier P (1958). Nonparametric estimation from incomplete observations. J Am Stat Assoc 53: 457–481
Massart P (1990). The tight constant in the Dvoretzky–Kiefer–Wolfowitz inequality. Ann Probab 18: 1269–1283
McKeague IW and Zhao Y (2006). Width-scaled confidence bands for survival functions. Stat Probab Lett 76: 327–339
Meier, P (1975) Estimation of a distribution function from incomplete observations. In Perspectives in probability and statistics (papers in honour of M. S. Bartlett on the occasion of his 65th birthday). Applied Probability Trust, Univ. Sheffield, Sheffield, pp. 67–87
Nair VN (1981). Plots and tests for goodness of fit with randomly censored data. Biometrika 68: 99–103
Pollard D (1990) Empirical processes: theory and applications. NSF-CBMS regional conference series in probability and statistics, 2, Institute of Mathematical Statistics, Hayward, CA
Shorack GR, Wellner JA (1986) Empirical processes with applications to statistics. Wiley series in probability and mathematical statistics: probability and mathematical statistics. Wiley, New York
Stute W (1994). Convergence of the Kaplan–Meier estimator in weighted sup-norms. Stat Probab Lett 20: 219–223
Stute W (1994). Strong and weak representations of cumulative hazard function and Kaplan–Meier estimators on increasing sets. J Stat Plan Inference 42: 315–329
Stute W and Wang J-L (1993). The strong law under random censorship. Ann Stat 21: 1591–1607
van de Geer S (1991) The entropy bound for monotone functions. Tech Rep Report 91-10, University of Leiden
van de Geer S (1993). Hellinger-consistency of certain nonparametric maximum likelihood estimators. Ann Stat 21: 14–44
van de Geer SA (2000) Applications of empirical process theory, vol. 6 of Cambridge series in statistical and probabilistic mathematics. Cambridge University Press, Cambridge
van der Vaart AW, Wellner JA (1996) Weak convergence and empirical processes. Springer Series in Statistics, Springer-Verlag, New York. With applications to statistics
Wang JG (1987). A note on the uniform consistency of the Kaplan–Meier estimator. Ann Stat 15: 1313–1316
Ying Z (1989). A note on the asymptotic properties of the product-limit estimator on the whole line. Stat Probab Lett 7: 311–314
Author information
Authors and Affiliations
Corresponding author
Additional information
Supported in part by NSF grant DMS-0503822 and by NI-AID grant 2R01 AI291968-04.
Rights and permissions
About this article
Cite this article
Wellner, J.A. On an exponential bound for the Kaplan–Meier estimator. Lifetime Data Anal 13, 481–496 (2007). https://doi.org/10.1007/s10985-007-9055-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10985-007-9055-z