Skip to main content
SpringerLink
Log in

Enhanced heat transfer rate analysis with inertial drag effect in a micropolar nanofluid flow within a channel: response surface methodology

  • Published:
Journal of Thermal Analysis and Calorimetry Aims and scope Submit manuscript

Abstract

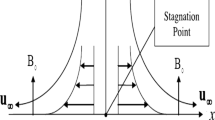
Analysing the basic need in industries and production of several engineering equipment for the cooling processes, the present problem deals with the two-dimensional flow of electrically conducting polar nanofluid between a parallel channel. The channel is filled with porous matrix, and the flow profiles are enhanced by incorporating several physical phenomena like thermal buoyancy, radiating heat, and the external heat source. The governing nonlinear coupled problem is distorted into non-dimensional system using similarity transformation, and then, numerical treatment is adopted for their solution. As a novelty, for the optimizing heat transfer rate a new statistical approach is adopted, i.e. response surface methodology. With the help of analysis of variance, regression analysis is presented considering several factors. Further, the behaviour of the heat transfer rate is shown taking single as well as interaction terms. Finally, the observation reveals that: increasing the particle concentration plays a significant role in promoting heat dissipation from the surface region, resulting in a cooling effect and a decrease in surface temperature. However, both the Reynolds number and thermal radiation have a greater impact on enhancing the fluid temperature, regardless of the heat source effect.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Abbreviations

\(T_{1}\) :

Temperature at bottom wall

\(T_{2}\) :

Temperature at top wall

\(g_{1}\) :

Gravitational force (m s−2)

\(\beta\) :

Thermal expansion coefficient

\(T\) :

Fluid temperature

\(v_{0}\) :

Suction/injection

\(k\) :

Vortex viscosity (kg·m−1·s−1)

\(B_{0}\) :

Magnetic strength

\(N\) :

Microrotation velocity

\(q_{0}\) :

Heat source/sink

\(Kp^{*}\) :

Permeability

\(j\) :

Micro inertia

\(Da\) :

Porous parameter

\(m\) :

Boundary parameter

\(k^{ * }\) :

Mean absorption coefficient

\(q_\text{rad}\) :

Thermal radiation heat flux

\(c_{\text p}\) :

Specific heat (J⋅kg−1⋅K−1)

\(\sigma\) :

Electric conductivity (S m−1)

\(M\) :

Magnetic Parameter

\(K\) :

Micropolar parameter

\(Rd\) :

Radiation parameter

\(S\) :

Heat generation parameter

\(C_{\text f}\) :

Skin friction coefficient

\(Nu_{\text x}\) :

The local Nusselt number

\(\phi\) :

Particle concentration

\(u,v\) :

Velocity components (m/s)

\(Cb\) :

Drag coefficient

\({\text{Re}}\) :

Reynolds number

\(nf\) :

Nanofluid

\(f\) :

Base fluid

References

  1. Eringen AC. Simple micropolar fluids. Int J Eng Sci. 1964;2:205–17.

    Article  Google Scholar 

  2. Eringen AC. Theory of micropolar fluids. Indiana Univ Math J. 1966;16:1–18. https://doi.org/10.1512/iumj.1967.16.16001.

    Article  Google Scholar 

  3. Eringen AC. Theory of micropolar fluids. J Appl Math. 1972;38:480–95.

    Google Scholar 

  4. Mishra P, Kumar D, Kumar J, Abel-Haleem A-AC, Park IS, Yahila. Analysis of MHD Williamson micropolar fluid flow in non-darcian porous media with variable thermal conductivity. Case Study Therm Eng. 2022;36:102195.

    Article  Google Scholar 

  5. Saidulu B, Sreeram Reddy K. Evaluation of combined heat and mass transfer in hydromagnetic micropolar flow along a stretching sheet when viscous dissipation and chemical reaction is present. Partial Differ Equ Appl Math. 2023;7:100467.

    Article  Google Scholar 

  6. Mohanty B, Mishra SR, Pattanayak HB. Numerical investigation on heat and mass transfer effect of micropolar fluid over a stretching sheet through porous media. Alex Eng J. 2015;54:223–32. https://doi.org/10.1016/j.aej.2015.03.010.

    Article  Google Scholar 

  7. Usafzai WK, Aly EH. Multiple exact solution for micropolar slip flow and heat transfer of a bidirectional moving plate. Therm Sci Eng Progress. 2023;37:101584.

    Article  Google Scholar 

  8. Gumber P, Yaseen M, Rawet SK, Kumar M. Heat transfer in micropolar hybrid nanofluids flow past a vertical plate in the presence of thermal radiation and suction effects. Partial Differ Equ Appl Math. 2022;5:100240.

    Article  Google Scholar 

  9. Goud BS, Nandeppanavar MM. Partial differential equations in applied. Mathematics. 2021;4:100104.

  10. Sibanda F, Awas FG. Flow of a Micropolar Fluid in Channel with Heat and Mass Transfer. Fluid Mech Heat Mass Transf. 90/mca26020041

  11. Mishra SR, Pattnaik PK, Dash GC. Effect of heat source and double stratification on MHD free convection in a micropolar fluid. Alex Eng J. 2015;54:681–9. https://doi.org/10.1016/j.aej.2015.04.010.

    Article  Google Scholar 

  12. Kumar M, Mahdy A. study of differential transform technique for transient hydro magnetic Jeffrey fluid flow from a stretching. Sheet Nonlinear Eng. 2020;9(1):145–55.

    Article  Google Scholar 

  13. Mondal P, Mukherjee S. Viscous dissipation effects on the limiting values of Nusselts numbers for a shear driven flow between two asymmetrically heated parallel plates. Front Heat Mass Transf (FHMT). 2012. https://doi.org/10.5098/hmt.v3.3.3004.

    Article  Google Scholar 

  14. DasGupta D, Mondal PK, Chakraborty S. Thermo capillary-actuated contact-line motion of immiscible binary fluids over substrtes with patterned wettability in narrow confinement. Phys Rev E. 2014;90:023011. https://doi.org/10.1103/PhysRevE.90.023011.

    Article  CAS  Google Scholar 

  15. Sarma R, Gaikwad H, Monal PK. Effect of conjugate heat transfer on entropy generation in slip-driven micro flow of power law fluids, nanoscale micro scale thermo Phys. Eng. 2017;21:26–44.

    CAS  Google Scholar 

  16. Reddy SRR, Anki Reddy PB. Thermal radiation effect on unsteady three-dimensional MHD flow of micropolar fluid over a horizontal surface of a parabola of revolution. Propuls Power Res. 2022;11:129–42. https://doi.org/10.1016/j.jppr.2022.01.001.

    Article  Google Scholar 

  17. Salahuddin T, Khan M, Al-Mubaddel FS, Alam MM, Ahmad I. A study of heat and mass transfer micropolar fluid flow near the stagnation regions of an object. Case Stud Therm Eng. 2021;26:101064. https://doi.org/10.1016/j.csite.2021.101064.

    Article  Google Scholar 

  18. Mahood F, Samshuddin MD, Mishra SR. Characteristics of thermophoresis and brownian motion on radiative reactive micropolar fluid flow towards continuously moving flat plate: HAM solution. Math Comput Simul. 2022;191:187–202.

    Article  Google Scholar 

  19. Ali B, Shafiq A, Siddique I, Al-Mdallal Q, Jarad F. Significance of suction, gravity modulation, thermal radiation, and magnetohydrodynamic on dynamics of micropolar fluid subject to an inclined sheet via finite element approach. Case Stud Therm Eng. 2021;28:101537. https://doi.org/10.1016/j.csite.2021.101537.

    Article  Google Scholar 

  20. Ali Shah N, Wakif A, Ei-Zahar ER, Ahmad S, Yook S-J. Numerical simulation of a thermally enhanced EMHD flow of a heterogeneous micropolar mixture comprising (60%)-ethylene glycol (EG), (40%)-water (W), and copper oxide nanomaterials (CuO). Case Stud Therm Eng. 2022;35:102046.

    Article  Google Scholar 

  21. Dogonchi AS, Waqas M, Seyyedi SM, Hashemi-Tilehnoee M, Ganji DD. CVFEM analysis for Fe3O4–H2O nanofluid in an annulus subject to thermal radiation. Int J Heat Mass Transf. 2019;132:473–83. https://doi.org/10.1016/j.ijheatmasstransfer.2018.11.124.

    Article  CAS  Google Scholar 

  22. Hashemi-Tilehnoee M, Dogonchi AS, Seyyedi SM, et al. Magnetohydrodynamic natural convection and entropy generation analyses inside a nanofluid-filled incinerator-shaped porous cavity with wavy heater block. J Therm Anal Calorim. 2020;141:2033–45. https://doi.org/10.1007/s10973-019-09220-6.

    Article  CAS  Google Scholar 

  23. Seyyedi SM, Dogonchi AS, Ganji DD, et al. Entropy generation in a nanofluid-filled semi-annulus cavity by considering the shape of nanoparticles. J Therm Anal Calorim. 2019;138:1607–21. https://doi.org/10.1007/s10973-019-08130-x.

    Article  CAS  Google Scholar 

  24. Tayebi T, Dogonchi AS, Karimi N, Ge-JiLe H, Chamkha AJ, Elmasry Y. Thermo-economic and entropy generation analyses of magnetic natural convective flow in a nanofluid-filled annular enclosure fitted with fins. Sustain Energy Technol Assess. 2021;46: 101274.

    Google Scholar 

  25. Sharma RP, Madhukesh JK, Shukla S, Prasannakumara BC. Numerical and Levenberg–Marquardt backpropagation neural networks computation of ternary nanofluid flow across parallel plates with Nield boundary conditions. Eur Phys J Plus. 2023;138:63. https://doi.org/10.1140/epjp/s13360-023-03680-4.

    Article  CAS  Google Scholar 

  26. Shamshuddin MD, Sharma RP. Thermal elaboration of ethylene glycol-based magnetized nanostructures via a convective permeable heated vertical surface employing modified buongiorno model. J Magn Magn Mater. 2023;571:170588. https://doi.org/10.1016/j.jmmm.2023.170588.

    Article  CAS  Google Scholar 

  27. Prakash Om, Sandeep N, Sharma RP, Rao PS. Influence of radiative heat on MHD Cu-Si/water dusty-nanoliquid flow above an enlarging sheet. Waves Random Complex Media. 2022. https://doi.org/10.1080/17455030.2022.2141470.

    Article  Google Scholar 

  28. Prakash Om, Barman P, Rao PS, Sharma RP. MHD free convection in a partially open wavy porous cavity filled with nanofluid. Numer Heat Trans Part A Appl. 2023;84(5):449–63. https://doi.org/10.1080/10407782.2022.2132330.

    Article  Google Scholar 

  29. Gireesha BJ, Anitha L. Irreversibility analysis of micropolar nanofluid flow using Darcy-Forchheimer rule in an inclined microchannel with multiple slip effects. Heat Transfer. 2022;51(6):5834–56.

    Article  Google Scholar 

  30. Ahmad S, Ali K, Haider T, Hussain SM. Thermal characteristics of kerosene oil-based hybrid nanofluids (Ag-MnZnFe2O4): a comprehensive study. Front Energy Res. 2023;12(4):123–45.

    Google Scholar 

  31. Ahmad S, Ashraf M, Ali K. Simulation of thermal radiation in a micropolar fluid flow through a porous medium between channel walls. J Therm Anal Calorim. 2021;144:941–53. https://doi.org/10.1007/s10973-020-09542-w.

    Article  CAS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, ITER, Siksha ‘O’ Anusandhan Deemed to be University, Bhubaneswar, Odisha, 751030, India

    Rupa Baithalu & S. R. Mishra

Authors
  1. Rupa Baithalu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. R. Mishra
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All the authors have equally contributed to complete the manuscript, i.e. RB has formulated the problem and verified the problem statement, and SRM has completed the draft with results and discussion section and checked the overall.

Corresponding author

Correspondence to S. R. Mishra.

Ethics declarations

Conflict of interest

There is no conflict of interest to publish our paper in your esteemed journal.

Data availability

No data are used.

Ethical approval

The entire work is the original work of the authors.

Consent for publication

All the authors have given their consent to publish the paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Baithalu, R., Mishra, S.R. Enhanced heat transfer rate analysis with inertial drag effect in a micropolar nanofluid flow within a channel: response surface methodology. J Therm Anal Calorim 148, 12159–12173 (2023). https://doi.org/10.1007/s10973-023-12483-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10973-023-12483-9

Keywords

Search

Navigation