How to Deal with Non-Convex Frontiers in Data Envelopment Analysis

Abstract

In data envelopment analysis, we are often puzzled by the large difference between the constant-returns-scale and variable returns-to-scale scores, and by the convexity production set syndrome in spite of the S-shaped curve, often observed in many real data sets. In this paper, we propose a solution to these problems. Initially, we evaluate the constant-returns-scale and variable returns-to-scale scores for all decision-making units by means of conventional methods. We obtain the scale-efficiency for each decision-making unit. Using the scale-efficiency, we decompose the constant-returns-scale slacks for each decision-making unit into scale-independent and scale-dependent parts. Following this, we eliminate scale-dependent slacks from the data set, and thus obtain a scale-independent data set. Next, we classify decision-making units into several clusters, depending either on the degree of scale-efficiency or on some other predetermined characteristics. We evaluate slacks of scale-independent decision-making units within the same cluster using the constant-returns-scale model, and obtain the in-cluster slacks. By summing the scale-dependent and the in-cluster slacks, we define the total slacks for each decision-making unit. Following this, we evaluate the efficiency score of the decision-making unit and project it onto the efficient frontiers, which are no longer guaranteed to be convex and are usually non-convex. Finally, we define the scale-dependent data set by which we can find the scale elasticity of each decision-making unit. We apply this model to a data set of Japanese universities’ research activities.

Appendices

Appendix A: Clustering Using Returns-to-Scale and Scale-Efficiency

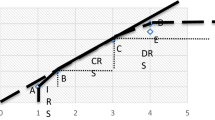
We already know the returns-to-scale (RTS) characteristics of each DMU, $i.e.$, increasing-returns-to-scale (IRS), CRS or DRS (decreasing returns-to-scale), as it is obtained from the VRS solution by projecting VRS inefficient DMUs onto the VRS efficient frontiers. We first classify CRS DMUs as Cluster C. Then, we classify IRS DMUs depending on the degree of scale-efficiency, $\sigma$. For example, IRS DMUs with 1$>\sigma \ge$0.8 are classified as I1, and IRS DMUs with 0.8$>\sigma \ge$0.6 as I2, and so on. DRS DMUs with 1$>\sigma \ge$0.8 are classified as D1, and so on, as above. We determine the number of clusters and their bandwidth by considering the number of DMUs in the cluster. Each cluster is expected to have at least as many DMUs as a few times the sum of the input and output factors. Figure 10 illustrates this point. This figure corresponds to the input-oriented case, where DMUs with highly different input scales may be classified into the same cluster. If such classification is inappropriate, we may try the output-oriented, non-oriented or directional distance models to determine clusters.

Fig. 10

Clustering by the degree of scale-efficiency

Appendix B: Proof of Propositions

Proposition 3.1

$\theta _k^{\mathrm{{SAS}}} \ge \theta _k^{\mathrm{{CRS}}} \quad (k=1,\ldots ,n).$

Proof

The CRS scores for $({\mathbf {x}}_k,{\mathbf {y}}_k )$ and $({\overline{\mathbf {x}}}_k,{\overline{\mathbf {y}}}_k )$, respectively, are defined by:

$$\begin{aligned} \begin{array}{l} \text{[CRS] }\quad \theta _k^{CRS} :=\mathop {\min }\limits _{{\varvec{\lambda }},{\mathbf {s}}^-,{\mathbf {s}}^+} \left( {1-\frac{1}{m}\sum \nolimits _{i=1}^m {\frac{s_i^- }{x_{ik} }} }\right) \\ \quad \;\quad \quad \text{ s.t. } {\mathbf {X}}{\varvec{\lambda }}+{\mathbf {s}}^-={\mathbf {x}}_k,{\mathbf {Y}}{\varvec{\lambda }}-{\mathbf {s}}^+={\mathbf {y}}_k,{\varvec{\lambda }}\ge {\mathbf {0}},{\mathbf {s}}^-\ge {\mathbf {0}},{\mathbf {s}}^+\ge {\mathbf {0}}, \\ \end{array} \end{aligned}$$

(B.1)

and

$$\begin{aligned} \begin{array}{l} [\text{ SAS] } \theta _k^{\mathrm{{SAS}}} :=\mathop {\min }\limits _{{\varvec{\mu }},{\mathbf {s}}^{\mathrm{{cl}}-},{\mathbf {s}}^{\mathrm{{cl}}+}} \left( {1-\frac{1}{m}\sum \nolimits _{i=1}^m {\frac{s_i^{\mathrm{{cl}}-} +(1-\sigma _k )s_i^{-*} }{\bar{x}_{ik} }} }\right) \\ \text{ s.t. } \overline{\mathbf {X}} {\varvec{\mu }}+{\mathbf {s}}^{\mathrm{{cl}}-}={\overline{\mathbf {x}}}_k ,\overline{\mathbf {Y}} {\varvec{\mu }}-{\mathbf {s}}^{\mathrm{{cl}}+}={\overline{\mathbf {y}}}_k,\mu _j =0(\forall j:\\ \text{ Cluster }(j)\ne \text{ Cluster }(k)),\;{\varvec{\mu }}\ge {\mathbf {0}},{\mathbf {s}}^{\mathrm{{cl}}-}\ge {\mathbf {0}},{\mathbf {s}}^{\mathrm{{cl}}+}\ge {\mathbf {0}}. \\ \end{array} \end{aligned}$$

(B.2)

We prove this proposition for two individual cases.

(Case 1) All DMUs belong to the same cluster.

In this case (B.2) becomes:

$$\begin{aligned} \begin{array}{l} [\text{ SAS }]\quad \quad \quad \theta _k^{\mathrm{{SAS}}} :=\mathop {\min }\limits _{{\varvec{\lambda }},\mathbf {t}^-,{\mathbf {t}}^+} \left( {1-\frac{1}{m}\sum \nolimits _{i=1}^m {\frac{t_i^- +(1-\sigma _k )s_k^{-*} }{\bar{x}_{ik} }} }\right) \\ \quad \quad \quad \quad \quad \text{ s.t. }\quad \overline{\mathbf {X}} {\varvec{\lambda }}+{\mathbf {t}}^-={\overline{\mathbf {x}}}_k \;,\overline{\mathbf {Y}} {\varvec{\lambda }}-{\mathbf {t}}^+={\overline{\mathbf {y}}}_k,{\varvec{\lambda }}\ge {\mathbf {0}},{\mathbf {t}}^-\ge {\mathbf {0}},{\mathbf {t}}^+\ge {\mathbf {0}}. \\ \end{array} \end{aligned}$$

(B.3)

Let $({\varvec{\lambda }}^*,{\mathbf {t}}^{-*},{\mathbf {t}}^{+*})$ be an optimal solution for (B.3). Since $P({\mathbf {X}},{\mathbf {Y}})=P(\overline{\mathbf {X}} ,\overline{\mathbf {Y}} )$ by Lemma 3.1, and both sets have the same efficient DMUs which span $({\overline{\mathbf {x}}}_k ,{\overline{\mathbf {y}}}_k )\;$, we have:

$$\begin{aligned} {\mathbf {X}}{\varvec{\lambda }}^*+{\mathbf {t}}^{-*}={\overline{\mathbf {x}}}_k ={\mathbf {x}}_k -(1-\sigma _k ){\mathbf {s}}_k^{-*},\;{\mathbf {Y}}{\varvec{\lambda }}^*-{\mathbf {t}}^{+*}={\overline{\mathbf {y}}}_k ={\mathbf {y}}_k +(1-\sigma _k ){\mathbf {s}}_k^{+*}. \end{aligned}$$

(B.4)

$$\begin{aligned} \mathrm{Hence,\,we\,have:}\,{\mathbf {X}}{\varvec{\lambda }}^*+{\mathbf {t}}^{-*}+(1-\sigma _k ){\mathbf {s}}_k^{-*} ={\mathbf {x}}_{k},\;{\mathbf {Y}}{\varvec{\lambda }}^*-{\mathbf {t}}^{+*}-(1-\sigma _k ){\mathbf {s}}_k^{+*} ={\mathbf {y}}_k. \end{aligned}$$

(B.5)

This indicates that $({\varvec{\lambda }}^*,{\mathbf {t}}^{-*}+(1-\sigma _k ){\mathbf {s}}_k^{-*} ,{\mathbf {t}}^{+*}+(1-\sigma _k ){\mathbf {s}}_k^{+*} )$ is feasible for (B.1), and hence its objective function value is not less than the optimal value, $\theta _k^{\mathrm{{CRS}}}$.

$$\begin{aligned} \theta _k^{\mathrm{{SAS}}} =1-\frac{1}{m}\sum \nolimits _{i=1}^m {\frac{t_i^{-*} +(1-\sigma _k )s_{ik}^{-*} }{x_{ik} }} \ge \theta _k^{\mathrm{{CRS}}}. \end{aligned}$$

(B.6)

Conversely, ${\mathbf {t}}^{-*} =\sigma _k {\mathbf {s}}_k^{-*}\,\text{ and }\,{\mathbf {t}}^{+*} =\sigma _k {\mathbf {s}}_k^{+*}$ are feasible for SAS, and hence it holds that $\theta _k^{\mathrm{{SAS}}} =\theta _k^{\mathrm{{CRS}}} \,(k=1,\ldots ,n).$

(Case 2) Multiple clusters exist.

In this case, we have additional constraints to (B.3) to define the cluster restriction, as follows:

$$\begin{aligned} \begin{array}{l} [\text{ SAS }]\quad \theta _k^{\mathrm{{SAS}}} :=\min 1-\frac{1}{m}\sum \nolimits _{i=1}^m {\frac{t_i^- +(1-\sigma _k )s_i^{-*} }{\bar{x}_{ik} }} \\ \qquad \qquad \text{ s.t. }\quad \overline{\mathbf {X}} {\varvec{\lambda }}+{\mathbf {t}}^-={\overline{\mathbf {x}}}_k \;,\overline{\mathbf {Y}} {\varvec{\lambda }}-{\mathbf {t}}^+={\overline{\mathbf {y}}}_{k},\lambda _j =0(\forall j:\text{ Cluster }(j)\ne \text{ Cluster }(k)),\\ \qquad \qquad {\varvec{\lambda }}\ge {\mathbf {0}},{\mathbf {t}}^-\ge {\mathbf {0}},{\mathbf {t}}^+\ge {\mathbf {0}}. \end{array} \end{aligned}$$

(B.7)

Since adding constraints results in an increase of the objective value, it holds that:

$$\begin{aligned} \theta _k^{\mathrm{{SAS}}} \ge \theta _k^{\mathrm{{CRS}}}. \end{aligned}$$

(B.8)

$\square$

Proposition 3.2

If $\theta _o^{\mathrm{{CRS}}} =1$, then it holds that $\theta _o^{\mathrm{{SAS}}} =\theta _o^{\mathrm{{CRS}}}$, but not vice versa.

Proof

If $\theta _k^{\mathrm{{CRS}}} =1$, then we have ${\mathbf {s}}_k^{-*} ={\mathbf {0}}\,\text{ and } {\mathbf {s}}_k^{+*} ={\mathbf {0}}$. Hence, we have total slacks=0 and $\theta _k^{\mathrm{{SAS}}} =1$. The converse is not always true, as demonstrated in the example below, where all DMUs belong to an independent cluster.

DMU	(l)x	(O)y	Cluster
A	2	2	a
B	4	2	b
C	6	2	c

DMU	CRS-I	SAS-I	Cluster
A	1	1	a
B	0.5	1	b
C	0.3333	1	c

$\square$

Proposition 3.3

SAS decreases with increasing input and decreasing output so long as both DMUs remain in the same cluster.

Proof

Let $( {{\mathbf {x}}_p,{\mathbf {y}}_p })\,\,\text{ and } ( {{\mathbf {x}}_{q},{\mathbf {y}}_q })\,\text{ with } {\mathbf {x}}_p \le {\mathbf {x}}_q \,\text{ and } {\mathbf {y}}_p \ge {\mathbf {y}}_q$ be the original and varied DMUs, respectively, in the same cluster. Let ${\mathbf {x}}_q ={\mathbf {x}}_p +{\varvec{\delta }}_p^- \;({\varvec{\delta }}_p^- \ge {\mathbf {0}}),{\mathbf {y}}_q ={\mathbf {y}}_p -{\varvec{\delta }}_p^+ \;({\varvec{\delta }}_p^+ \ge {\mathbf {0}})$ and the optimal solution for $( {{\mathbf {x}}_{p},{\mathbf {y}}_p })\,$ be $(\theta _p^{\mathrm{{SAS}}},{\varvec{\lambda }}_p^*,{\mathbf {s}}_p^{-*},{\mathbf {s}}_p^{+*} )$. We have ${\mathbf {X}}{\varvec{\lambda }}_p^*+{\mathbf {s}}_p^{-*} ={\mathbf {x}}_p ={\mathbf {x}}_q -{\varvec{\delta }}_p^-, \quad {\mathbf {Y}}{\varvec{\lambda }}_p^*-{\mathbf {s}}_p^{+*} ={\mathbf {y}}_p ={\mathbf {y}}_q +{\varvec{\delta }}_p^+$. Hence $({\mathbf {s}}_p^{-*} +{\varvec{\delta }}_p^- ,{\mathbf {s}}_p^{+*} +{\varvec{\delta }}_p^+ )$is a feasible slack for $( {{\mathbf {x}}_{q},{\mathbf {y}}_q })\,$. We have

$$\begin{aligned} \theta _p^{\mathrm{{SAS}}}&= 1-\frac{1}{m}\sum \nolimits _{i=1}^m {\frac{s_{ip}^{-*} }{x_{ip} }} =1-\frac{1}{m}\sum \nolimits _{i=1}^m {\frac{s_{ip}^{-*} }{x_{iq} -\delta _p^- }}\\&\ge 1-\frac{1}{m}\sum \nolimits _{i=1}^m {\frac{s_{ip}^{-*} +\delta _p^- }{x_{iq} }} \ge \theta _q^{\mathrm{{SAS}}}. \end{aligned}$$

$\square$

Proposition 3.4

The projected DMU $(\overline{{\overline{{\mathbf {x}}}}}_k ,\overline{{\overline{{\mathbf {y}}}}}_k )$ is efficient under the SAS model among the DMUs in its containing cluster. It is CRS and VRS efficient among the DMUs in its cluster.

Proof

From the definition of $(\overline{{\overline{{\mathbf {x}}}}}_k ,\overline{{\overline{{\mathbf {y}}}}}_k )$, it is SAS efficient. Thus, it is CRS and VRS efficient in its cluster. $\square$

Proposition 5.1

$$\begin{aligned} 1\ge \theta _k^{scale} \ge \max (\theta _k^{\mathrm{{CCR}}},\sigma _k ). \end{aligned}$$

(B.9)

Proof

$$\begin{aligned} \sigma _k +\theta _k^{\mathrm{{CCR}}} -\sigma _k \theta _k^{\mathrm{{CCR}}}&= \sigma _k (1-\theta _k^{\mathrm{{CCR}}} )+\theta _k^{\mathrm{{CCR}}} \\&= \theta _k^{\mathrm{{CCR}}} (1-\sigma _k )+\sigma _k \ge \max \left\{ {\sigma _{k},\theta _k^{\mathrm{{CCR}}} } \right\} . \end{aligned}$$

This term is increasing in $\sigma _k$ and is equal to 1 when $\sigma _k$=1. $\square$

Proposition 5.2

$$\begin{aligned} \theta _k^{scale} =1\;\mathrm{if\,and\,only\,if}\,\sigma _k =1. \end{aligned}$$

(B.10)

Proof

If $\sigma _k =1$, it holds $\theta _k^{scale} =\sigma _k +\theta _k^{\mathrm{{CCR}}} -\sigma _k \theta _k^{\mathrm{{CCR}}} =1.$ Conversely, if $\theta _k^\mathrm{{scale}} =\sigma _k +\theta _k^{\mathrm{{CCR}}} -\sigma _k \theta _k^{\mathrm{{CCR}}} =1$, we have $\sigma _k (1-\theta _k^{\mathrm{{CCR}}} )=1-\theta _k^{\mathrm{{CCR}}}$. Hence, if $\theta _k^{\mathrm{{CCR}}} <1$, then it holds $\sigma _k =1.$ If $\theta _k^{\mathrm{{CCR}}} =1$, then we have $\theta _k^{\mathrm{{BCC}}} =1\;\text{ and }\,\sigma _k =1.$ $\square$